Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
f(t) = 3 −7/4t, (1/3,-9/4)
f(1/3)
Answers
The slope of the graph of function f(t) at the point (1/3,-9/4) is -7/4. This was obtained by finding the derivative of the function and evaluating it at t = 1/3. The result was confirmed using a graphing utility.
To find the slope of the graph of the function f(t) at the point (1/3, -9/4), we need to find the derivative of the function and evaluate it at t = 1/3.
Taking the derivative of f(t), we get:
f'(t) = -7/4
This means that the slope of the graph of f(t) is a constant value of -7/4 at every point on the graph.
To confirm this result using a graphing utility, we can plot the function f(t) and its tangent line at t = 1/3. The slope of the tangent line should be equal to the derivative of f(t) at t = 1/3.
Using an online graphing tool, we can plot the function f(t) = 3 - 7/4t and its tangent line at t = 1/3, which passes through the point (1/3, -9/4). The tangent line has the equation:
y - (-9/4) = (-7/4)(x - 1/3)
Simplifying, we get:
y = -7/4x - 3/4
The slope of this tangent line is -7/4, which matches the derivative of f(t) at t = 1/3. Therefore, our answer is confirmed.
To know more about Slope, visit:
brainly.com/question/2491620
#SPJ11
Related Questions
Ayuda Porfavor !!!!!!!!

Answers
Answer:
44
Step-by-step explanation:
10 x 3 = 30
8 + 6 =14
30 + 14 = 44
Answer:
110ft²
Step-by-step explanation:
Area of figure=(10×8)+(1/2×6×8)
=80+24
=112 ft²
=110 ft² (to nearest tenth)
Choose two ordered pair that will satisfy the inequality 1. y < x + 3 ; (2, 5), (5, 2), ( -5, -5), ( 4, 0) 2. 3x + y > 10; ( -1, 2), ( 1, 10) , ( 3, 1), (3, 3) 3. 2y + x ≥ 5; (1, 2), (0,4), ( 2,2), ( -1, -5) 4. 3x - 2y ≤ 10; ( 5,1), (0,-5), (-1, -6), (10, 2) 5. 5x + 3y > 15; ( 2,1), (-3, 1), (0, 6), ( 2, 2)
Answers
We have found the two ordered pairs that satisfy the given inequality in each case. In this question, we need to choose two ordered pairs that will satisfy each case's given inequality. Let's evaluate each inequality using each of the given ordered pairs to find the solution.
1. y < x + 3
Using the given ordered pairs, we have:
(2, 5): 5 < 2 + 3, which is true.
(5, 2): 2 < 5 + 3, which is false.
(-5, -5): -5 < -5 + 3, which is false.
(4, 0): 0 < 4 + 3, which is true.
The two ordered pairs that satisfy the given inequality are (2, 5) and (4, 0).
2. 3x + y > 10
Using the given ordered pairs, we have:
(-1, 2): 3(-1) + 2 > 10, which is false.
(1, 10): 3(1) + 10 > 10, which is true.
(3, 1): 3(3) + 1 > 10, which is true.
(3, 3): 3(3) + 3 > 10, which is true.
The two ordered pairs that satisfy the given inequality are (1, 10), (3, 1), and (3, 3).
3. 2y + x ≥ 5
Using the given ordered pairs, we have:
(1, 2): 2(1) + 2 ≥ 5, which is true.
(0, 4): 2(4) + 0 ≥ 5, which is true.
(2, 2): 2(2) + 2 ≥ 5, which is false.
(-1, -5): 2(-5) - 1 ≥ 5, which is false.
The two ordered pairs that satisfy the given inequality are (1, 2) and (0, 4).
4. 3x - 2y ≤ 10 Using the given ordered pairs, we have:
(5, 1): 3(5) - 2(1) ≤ 10, which is true.
(0, -5): 3(0) - 2(-5) ≤ 10, which is true.
(-1, -6): 3(-1) - 2(-6) ≤ 10, which is false.
(10, 2): 3(10) - 2(2) ≤ 10, which is false.
The two ordered pairs that satisfy the given inequality are (5, 1) and (0, -5).
5. 5x + 3y > 15
Using the given ordered pairs, we have:
(2, 1): 5(2) + 3(1) > 15, which is false.
(-3, 1): 5(-3) + 3(1) > 15, which is false.
(0, 6): 5(0) + 3(6) > 15, which is true.
(2, 2): 5(2) + 3(2) > 15, which is false.
The only ordered pair that satisfies the given inequality is (0, 6). Thus, we have found the two ordered pairs that satisfy the given inequality in each case.
To know more about the ordered pairs, visit:
brainly.com/question/28874341
#SPJ11
Write and solve an equation to answer the question.A box contains orange balls and green balls. The number of green balls is nine more than five times thenumber of orange balls. If there are 123 balls altogether, then how mmany green balls and how manyorange balls are there in the box?There are_____orange balls and____green balls in the box.
Answers
Let
x -----> number of orange balls
y -----> number of green balls
we have that
x+y=123 -----> x=123-y ------> equation A
y=5x+9 -----> equation B
Solve the system of equations
substitute equation A in equation B
y=5(123-y)+9
solve for y
y=615-5y+9
y+5y=615+9
6y=624
y=104
Find out the value of x
x=123-104
x=19
therefore
There are 19 orange balls and 104 green balls in the boxwhat is 3/4 of 2483???
Answers
Answer:
1862.25
Step-by-step explanation:
.......
Terme und Gleichungen in die Alltagssprache übersetzen
197
Was bedeutet dieser Term? Schreibe einen passenden Text dazu an.
a) 5•uDas Fünffache einer Zahl
b) z + 12
c) a : 2 - 4
d) i•9
2
e) 34 + 7•V
f) (p - 7)•3
Answers
Step-by-step explanation:
find the points of intersection of the parabola 4y squared + 8 y - 16 x equal to 12 in the line x equals to 3
The Treasury auctioned $2. 5 billion par value 91-day T-bills, the following bids were received: Bidder Bid Amount Bid Price A $500 million $0. 9940 B $750 million $0. 9901 C $1. 5 billion $0. 9925 D $1 billion $0. 9936 E $600 million $0. 9939 The Treasury also received $750 million in noncompetitive bids. Who will receive T-bills, what quantity, and at what price
Answers
Average Auction Price is 0.9925the noncompetitive bidders will receive $750 million at a price of $0.9925 per $1 of par value.
To determine who will receive T-bills, what quantity, and at what price, we need to rank the bidders based on the bid prices and allocate the T-bills in descending order of bid prices until the entire $2.5 billion par value has been allocated. The bid prices listed are quoted as a percentage of par value, so we need to calculate the dollar amount bid for each bidder as follows:
Bid Amount = Bid Price × Par Value
For Bidder A:
Bid Amount = 0.9940 × 500 million
Bid Amount = $497 million
For Bidder B:
Bid Amount = 0.9901 × 750 million
Bid Amount = $742.6 million
For Bidder C:
Bid Amount = 0.9925 × 1.5 billion
Bid Amount = $1.48875 billion
For Bidder D:
Bid Amount = 0.9936 × 1 billion
Bid Amount = $993.6 million
For Bidder E:
Bid Amount = 0.9939 × 600 million
Bid Amount = $596.34 million
Total Bid Amount = $3.31874 billion
Since the total bid amount exceeds the $2.5 billion par value of the T-bills being auctioned, we need to allocate the T-bills to the highest bidders until the entire $2.5 billion has been allocated.
Ranking the bidders in descending order of bid prices, we have:
Bidder B with a bid price of $0.9901
Bidder C with a bid price of $0.9925
Bidder D with a bid price of $0.9936
Bidder E with a bid price of $0.9939
Bidder A with a bid price of $0.9940
Allocating T-bills to the highest bidders until the entire $2.5 billion par value has been allocated, we have:
Bidder B will receive $750 million at a price of $0.9901 per $1 of par value.
Bidder C will receive $750 million at a price of $0.9925 per $1 of par value.
Bidder D will receive $500 million at a price of $0.9936 per $1 of par value.
Bidder E will receive $250 million at a price of $0.9939 per $1 of par value.
The noncompetitive bids of $750 million will be allocated at the average auction price, which is calculated as the simple average of the four highest accepted bid prices:
Average Auction Price = (0.9901 + 0.9925 + 0.9936 + 0.9939) / 4
Average Auction Price = 0.9925
Therefore, the noncompetitive bidders will receive $750 million at a price of $0.9925 per $1 of par value.
To learn more about percentage click here
brainly.com/question/16797504
#SPJ4
(please help asap T-T) Using long division, find the quotient of (6x^3 + x^2 - 2x + 15) / (2x + 3)
a. 3x^2 - 4x + 5
b. 3x^2 + 5x - 6
c. 2x^2 + 3x - 5
d. 3x^2 - 5x - 5
Answers
The polynomial 6x³ + x² - 2x + 15 divided by 2x + 3 will give a quotient of 3x² - 4x + 5 and a remainder of zero, which makes option a correct.
How to calculate for the quotient and remainderThe long division method will require us to; divide, multiply, subtract, bring down the next number and repeat the process to end at zero or arrive at a remainder
We shall divide the polynomial 6x³ + x² - 2x + 15 by 2x + 3 as follows;
x³ divided by 2x equals 3x²
2x + 3 multiplied by 3x² equals 6x³ + 9x²
subtract 6x³ + 9x² from 6x³ + x² - 2x + 15 will result to -8x² - 2x + 15
-8x² divided by 2x equals -4x
2x + 3 multiplied by -4x equals -8x² - 12x
subtract -8x² - 12x from -8x² - 2x + 15 will result to 10x + 15
10x divided by 2x equals 5
2x + 3 multiplied by 5 equals 10x + 15
subtract 10x + 15 from 10x + 15 will result to a remainder of 0
Therefore by the long division method, 6x³ + x² - 2x + 15 divided by 2x + 3 gives a quotient 3x² - 4x + 5 and a remainder of 0.
Learn more about long division method here: https://brainly.com/question/25289437
#SPJ1
1 in. = 2 ft. what is the area of the actual living room?

Answers
Answer:
........................
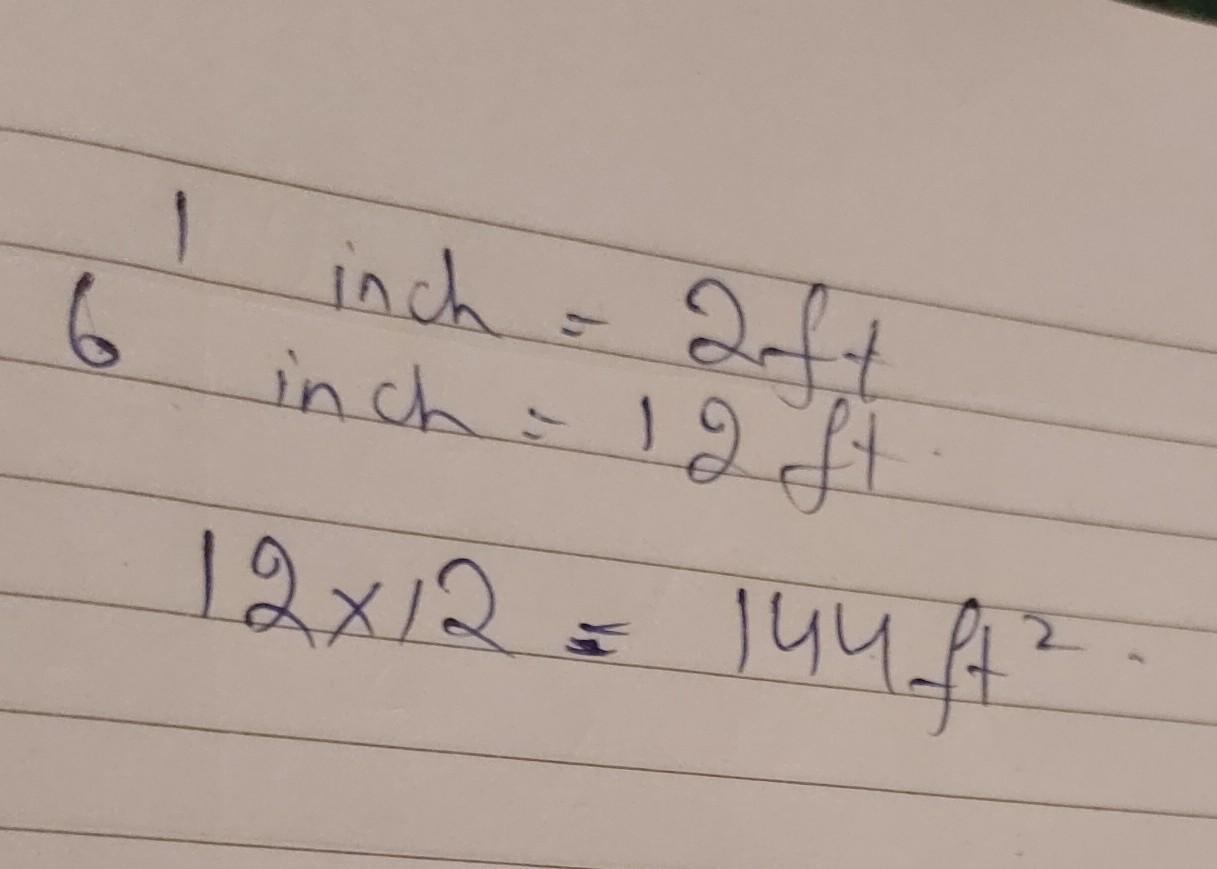
Answer:
\(144ft^{2}\) (144ft^2)
Step-by-step explanation:
Since the living room is 6 inches by 6 inches, the formula of the living room can be seen as: \(6in^{2}\). And since each inch is equal to 2 feet, (6*2=12) we can turn the equation into: \(12ft^{2}\). 12 times 12 is 144, so the answer is \(144ft^{2}\)
You need the sample for your survey to include people of different ages. You need some to be between the ages of 20-40, some to be between 40-60, and some to be 60-80. Which one of these types of sampling will help you get objects from each group:
Answers
Answer:
I would say a bar graph because it is used best for data that needs groups.
In order to get samples from each age group, you would need to use stratified sampling. This involves dividing the population into subgroups, or strata, based on a particular characteristic - in this case, age.
Once the population has been stratified, a random sample can be taken from each subgroup in proportion to its size.
For example, if the population consists of 1000 people, with 300 aged 20-40, 400 aged 40-60, and 300 aged 60-80, you would need to take a sample of 60 people (20% of the population) in order to get 20 people from each age group. This could be done by randomly selecting 18 people from the 20-40 age group, 24 people from the 40-60 age group, and 18 people from the 60-80 age group.
Stratified sampling is often used when there are important subgroups within a population that need to be represented in the sample. It can help to ensure that the sample is representative of the population as a whole, and can improve the accuracy of the survey results. However, it can also be more time-consuming and expensive than other sampling methods.
To know more about stratified sampling, refer to the link below:
https://brainly.com/question/31051644#
#SPJ11
Jerica sells used motorcycles. she makes $300 per week plus $75 for each bicycle sold. she wants to earn $1059?per week. write an equation to find out how many motorcycles she must sell each week to accomplish this.
Answers
Answer: $684
Step-by-step explanation: Add 300 to 75 and you have 375, next subtract the total payment she wants to have per week (which is 1059) so, subtract 1059 to 375 then you have $684. To check your answer, add 684 to 375 and you come up with 1059.
how far from the base of a building must a 15-ft ladder be placed so that it reaches 12 ft up the wall?
Answers
The base of the ladder must be placed 3 ft from the base of the building. The total length of the ladder is 15 ft.
1. The ladder must reach 12 ft up the wall, so we need to calculate the distance from the base of the building to 12 ft.
2. The total length of the ladder is 15 ft.
3. Subtract the length of the ladder (15 ft) fromthe desired height (12 ft) to get the distance from the base of the building.
4. 12 ft - 15 ft = -3 ft
5. Since the distance cannot be negative, the base of the ladder must be placed 3 ft away from the base of the building.
Learn more about length here
https://brainly.com/question/13194650
#SPJ4
What is the domain of the graph below

Answers
Determine the type of triangle that is drawn below.
4.89
K
30
809
6.26
4.89
509
What type of triangle
Answers
Answer:
Isosoles triangleddndnndnendndne
(b) Find the lowest common multiple (LCM) of 450 and 315.
Answers
Answer:
The LCM of 315 and 450 is 3150. Hope this helps :)
Step-by-step explanation:
An old campfire is uncovered during an archaeological dig. Its charcoal is found to contain less than 1 1000 the normal amount of 14C. Estimate the minimum age of the charcoal (in years), noting that 210
Answers
An old campfire is uncovered during an archaeological dig. Its charcoal is found to contain less than 1/1000 the normal amount of 14C. Estimate the minimum age of the charcoal (in years), noting that 210
To estimate the minimum age of the charcoal, we can use the concept of half-life. The half-life of 14C is approximately 5730 years.
Since the charcoal is found to contain less than 1/1000 the normal amount of 14C, it means that more than 99.9% of the 14C has decayed.
To find the number of half-lives that have passed, we can use the equation:
(1/2)^n = 1/1000
Solving for n, we get:
n = log(1/1000) / log(1/2)
n ≈ 9.966
Since each half-life is approximately 5730 years, we can estimate the minimum age of the charcoal by multiplying the number of half-lives by the half-life time:
9.966 * 5730 ≈ 57,254 years
Therefore, the minimum age of the charcoal is approximately 57,254 years.
To know more about minimum visit:
https://brainly.com/question/29499469
#SPJ11
1. Use Horner's algorithm to find p(4), where p(z) = 3z^2 – 7z^4 – 5z^3+z^2 -- 8z +2. 2. (Continuation) For the polynomial of preceding problem, find its expansion in a Taylor series about the point z0 = 4. 3. (Continuation) For the polynomial of Problem 3.5.1 (above), start Newton's method at the point z0 = 4. What is z1?
Answers
Evaluating p(4) using Horner's algorithm:
1. To use Horner's algorithm, we write the polynomial in nested form as follows:
p(z) = ((3z - 7)z - 5)z^2 + (z - 8)z + 2
Now, we can evaluate p(4) by starting from the inside and working our way out:
p(4) = ((3(4) - 7)4 - 5)4^2 + (4 - 8)4 + 2
= (5)4^2 - 4 + 2
= 78
Therefore, p(4) = 78.
2. Finding the Taylor series expansion of p(z) about z0 = 4:
To find the Taylor series expansion of p(z) about z0 = 4, we need to compute the derivatives of p(z) at z0 = 4. First, we compute p'(z) = 6z^2 - 28z^3 - 10z^2 + 2z - 8, then p''(z) = 12z - 84z^2 - 20z + 2, p'''(z) = 12 - 168z - 20, and so on.
Using these derivatives, we can write the Taylor series expansion of p(z) about z0 = 4 as follows:
p(z) = p(4) + p'(4)(z - 4) + p''(4)(z - 4)^2/2! + p'''(4)(z - 4)^3/3! + ...
Substituting in the values we computed, we get:
p(z) = 78 + 10(z - 4) - 41(z - 4)^2/2! - 14(z - 4)^3/3! + ...
Therefore, the Taylor series expansion of p(z) about z0 = 4 is:
p(z) = 78 + 10(z - 4) - 20.5(z - 4)^2 - 2.333(z - 4)^3 + ...
3. Using Newton's method to find a root of p(z):
To use Newton's method to find a root of p(z), we start with an initial guess z0 = 4 and iterate the formula z1 = z0 - p(z0)/p'(z0) until we reach a desired level of accuracy.
4. We already computed p'(z) in part 2, so we can use the formula to compute z1 as follows:
z1 = z0 - p(z0)/p'(z0)
= 4 - (78 + 10(4) - 20.5(4 - 4)^2 - 2.333(4 - 4)^3)/[6(4)^2 - 28(4)^3 - 10(4)^2 + 2(4) - 8]
= 3.9167
We can continue to iterate using this formula to get better approximations for the root of p(z).
Horner's algorithm is a fast and efficient way to evaluate a polynomial at a particular point. It involves using the distributive property of multiplication to rewrite a polynomial in a nested form, then evaluating the polynomial from the inside out.
In this problem, we will use Horner's algorithm to evaluate p(4) for a given polynomial, find its Taylor series expansion about the point z0 = 4, and then use Newton's method to find an approximation for a root of the polynomial.
Know more about "Horner's algorithm" here:-
https://brainly.com/question/5150902#
#SPJ11
What is 15/20 closest to 0,1/2 or 1
Answers
Answer:
0.07 (7/100) is closer to 0.
1.150 (1150/1000) is closer to 1.
0.391 (391/1000) is closer to 1/2.
0.0999 (999/10,000) is closer to 0.
0.99 (99/100) is closer to 1.
0.599 (599/1000) is closer to 1/2.
Put everything as a fraction. The first spot after the decimal means you put the number over 10, the second place means you put it over 100, the third 1,000, fourth 10,000 and so on. Hope I helped! ^^Step-by-step explanation:
The closeness of the given function is found to be by writing it in the simplest form as 1.
What is a fraction?A fraction is a number written in the form a / b, where a and b are integers and b ≠ 0.
The number a is called as the numerator and b is the denominator.
The given fraction is 15/20.
It can be simplified as below,
Divide numerator and denominator by the common factor 5 as,
(15 ÷ 5)/(20 ÷ 5)
⇒ 3/4
The given fraction 3/4 is greater than zero and closest to 1.
Hence, the given fraction is closest to integer 1.
To know more about fraction click on,
https://brainly.com/question/10354322
#SPJ2
what is the x and y equal in y=8x+1 and y=3x+26
Answers
Answer:
x=5, y=41
Step-by-step explanation:
Because both equations are equal to Y, you can set them equal to each other like this:
8x+1=3x+26
From here, solve for x:
1. 5x+1=26
2. 5x=25
3. x=5
Once you have x, plug it back in to one of the original equations:
y=8(5)+1
y=41 and then you have your answer
If this answer was particularly helpful, please feel free to give it brainliest!! I would greatly appreciate it.
Answer:
(x, y) = (5, 41)
Step-by-step explanation:
y = 8x + 1
y = 3x + 26
Substituting the value of y (first equation) into the second equation, we get:
8x + 1 = 3x + 26
5x = 25
x = 5.
So, to get y, all we have to do is to substitute the value of x into the second equation.
y = 3 * 5 + 26
y = 15 + 26
y = 41
What is the median of the following 6 test scores?
64, 72, 85, 80, 72, 89
Answers
Answer:
76
Step-by-step explanation:
The given data is 64, 72, 85, 80, 72, 89.
First we arrange it in ascending order.
64,72,72,80,85,89
The middle two terms are 72 and 80.
There are 6 no of observations.
The median when n is even is given by :
\(M=\dfrac{72+80}{2}\\\\=76\)
So, the median of given data is 76.
Need help please show work

Answers
Answer:
Add the lengths:
5x - 16 + 2x - 4 = 7x - 20
NEED HELP ASAP
I’m just an idiot and need help SO PLEASE HELP ME IM DESPERATE

Answers
What is
2+3(4.3x00.009)
Answers
Answer:
The answer to 2+3(4.3 x 00.009) is 2.1161.
Step-by-step explanation:
Hope this helps!
Answer:
2.1161
Step-by-step explanation:
In the figure shown, polygons JKLMN and PQRST are congruent.
-8-6-4-2
K
N
8
6
4
2
-2
4
-6
T
2
4
$
6
8
Which sequence of transformations could be used to show the congruence of polygons JKLMN and PQRST?
A Reflect PQRST across the y-axis, and then translate the result down 10 units.
B. Reflect PQRST across the x-axis, and then translate the result down 10 units.
OC. Translate PQRST to the left 10 units, and the reflect the result across the x-axis.
D. Translate PQRST to the left 10 units, and then reflect the result across the y-axis.

Answers
The sequence of transformations used to show the congruence of polygons JKLMN and PQRST is to reflect PQRST across the y-axis and then translate the result down 10 units.
We are given two polygons. Both the polygons are congruent, and to prove it, we can use the concept of transformations. The first transformation we need to perform is to reflect the polygon PQRST across the y-axis. The next transformation that needs to be performed is to translate the result down by 10 units. We find that the polygon PQRST now coincides with the polygon JKLMN. Hence, it is proved that the polygons are congruent to each other.
To learn more about transformations, visit :
https://brainly.com/question/11709244
#SPJ9
The square of a proper fraction is:
a) Larger than fraction
b) Equal to the fraction
c) Smaller than the fraction
d) None of these
Please help & make sure to give an explanation for the answer
Answers
Answer:
c. Smaller than the fraction
Step-by-step explanation:
have a great night :)
3.......2........1.....
LET.. IT.. RIP
*who know what this is from* lol


Answers
Answer:
narato???????
Step-by-step explanation:
its from men dadd
Answer:
Beyblaes lol my brother used to love them. :)
Step-by-step explanation:
i need an expression for d and how far the star is from the sun

Answers
Step 1
Find the distance between the sun and the star using SohCahToa.
For this problem we use Toa.
\(\text{Tan}\theta=\frac{\text{opposite}}{\text{adjacent}}\)
where;
\(\begin{gathered} \theta=0.00001389^o \\ \text{adjacent}=\text{ d} \\ \text{Opposite}=\text{ 1 AU} \end{gathered}\)Step 2
Substitute and find the value of d
\(\begin{gathered} \text{Tan}0.00001389=\frac{1}{d} \\ d=\frac{1}{Tan0.00001389} \\ \end{gathered}\)\(d\text{ = 4}124966.128\text{ AU}\)
Write the number 347.85 in expanded form. a 3 + 100 + 4 x 10 + 7 x 1 x 8 x (1/100) + 5 x (1/100) b 3 x 100 + 4 + 10 + 7 x 1 + 8 x (1/100) + 5 x (1/10) c 3 x 100 + 4 x 10 + 7 x 1 + 8 x (1/10) + 5 x (1/100)
Answers
Answer:
C. 3 × 100 + 4 × 10 + 7 × 1 + 8 × (1/10) + 5 × (1/100)
Step-by-step explanation:
3: hundreds
4: tens
7: ones
8: tenths
5: hundreths
Which word problem below could be represented by the number sentence 6 X 4= ?
A. Luis had 6 pencils. He bought 4 more. How many pencils does he have?
B. Luis bought 6 packages of pencils with 4 pencils in each package. How many pencils did he buy?
O C. Luis had 6 pencils. He gave away 4. How many pencils does he have left?
O D. Luis had 6 pencils. He placed them in 4 groups. How many were in each group?
E. Luis bought 6 packages of pencils. 4 of the packages were free. How many packages did he have to pay for?
Answers
Answer:
O D. Luis had 6 pencils. He placed them in 4 groups. How many were in each group?
Step-by-step explanation:
this makes more sense, since he had 6 pencils and put them in 4 different groups. so, 6 *4 = 24 c:
Simplify by comibining like terms for x + 10y - 4y + 4x
Answers
Answer:
5x + 6y
Hope it helps!
Let ℤ be the set of all integers and let, (20) 0 = { ∈ ℤ| = 4, for some integer }, 1 = { ∈ ℤ| = 4 + 1, for some integer }, 2 = { ∈ ℤ| = 4 + 2, for some integer }, 3 = { ∈ ℤ| = 4 + 3, for some integer }. Is {0, 1, 2, 3 } a partition of ℤ? Explain your answer.
Answers
Answer:
\(\{0, 1, 2, 3\}\) is a partition of Z
Step-by-step explanation:
Given
\($$A _ { 0 } = \{n \in \mathbf { Z } | n = 4 k$$,\) for some integer k\(\}\)
\($$A _ { 1 } = \{ n \in \mathbf { Z } | n = 4 k + 1$$,\) for some integer k},
\($$A _ { 2 } = { n \in \mathbf { Z } | n = 4 k + 2$$,\) for some integer k},
and
\($$A _ { 3 } = { n \in \mathbf { Z } | n = 4 k + 3$$,\)for some integer k}.
Required
Is \(\{0, 1, 2, 3\}\) a partition of Z
Let
\(k = 0\)
So:
\($$A _ { 0 } = 4 k\)
\($$A _ { 0 } = 4 k \to $$A _ { 0 } = 4 * 0 = 0\)
\($$A _ { 1 } = 4 k + 1$$,\)
\(A _ { 1 } = 4 *0 + 1$$ \to A_1 = 1\)
\(A _ { 2 } = 4 k + 2\)
\(A _ { 2} = 4 *0 + 2$$ \to A_2 = 2\)
\(A _ { 3 } = 4 k + 3\)
\(A _ { 3 } = 4 *0 + 3$$ \to A_3 = 3\)
So, we have:
\(\{A_0,A_1,A_2,A_3\} = \{0,1,2,3\}\)
Hence:
\(\{0, 1, 2, 3\}\) is a partition of Z