Find the product
0.037 · 0.26
Answers
Explanation: .037 • .26 = 0.00962
0.037 • 0.26 = 0.00962
Related Questions
Information for Questions 5-7: The Annual Survey of Colleges in the U.S. also reports on the average amount of student loan debt by state. The most recent data by state showed an approximately normal shape with a minimum average amount of
$19,000
and a maximum average amount of
$38,000
. Use the minimum and maximum value and the normal shape to estimate the mean and standard deviation of the data for the 50 states. (Mean and standard deviation have been rounded to the nearest
$100
.) a. mean
=$25,000;
standard deviation
=$3,500
b. mean
=$26,800;
standard deviation
=$2,100
c. mean
=$26,800;
standard deviation
=$3,700
d. mean
=$28.500;
standard deviation
=$1,800
e. mean
=$28,500;
standard deviation
=$3,200
A federal study of student loan debt plans to focus on those states with the highest amounts of student loan debt. The study plans on targeting those states that fall in the top
2.5%
in terms of average student loan amounts. What is the cutoff point that would place a state in the top
2.5%
based on student loan debt? (Use the mean and standard deviation estimates from Question #5.) a.
$38,100
b.
$34,900
c.
$31,700
d.
$32,500
e.
$22,100
Answers
The correct answer is $34900.
X : Average amount of loan of student debt by state .
X = N ( μ = $28500 , σ² = ( 3200 )² )
To find : What is the cutoff point that would place a state in top 2.5%
Let it be X
P( X > x ) = 0.025
P(X-μ/σ > X - 28500/3200) = 0.025
P(z >Z ) = 0.025
1 - P(z<Z ) = 0.025
P(z<Z ) = 0.975
φ(z) = 0.975
Z = φ⁻¹(0.975)
X - 28500/3200 = 1.96
X = 34772
i.e; P(X > 34772) = 0.025
Since, it is nearly equal to $34900 option b is correct.
To learn more about cutoff point click here:
brainly.com/question/29031557
#SPJ4
For her party can Nina fill fewer than 10 bags with treats between 10 and 20 bags between 20 and 30 bags or more than 30 bags explain
Answers
The correct option regarding the number of bags filled by Nina, using proportions, is given as follows:
Between 20 and 30 bags.
What is a proportion?A proportion is a fraction of an amount, and this fraction is combined with the unit rates of the problem and basic arithmetic operations, especially multiplication and division, to find the desired amounts in the context of the problem.
In this problem, a proportion is applied to find the number of bags filled by Nina, which is given by the division presented as follows:
Number of bags = Number of treats / Treats per bag.
The values of these parameters are given as follows:
Number of treats: 78.Number of treats per bag: 3.Hence the numeric value of the expression is:
Number of bags = 78/3 = 26.
Which is a number between 20 and 30.
Missing InformationThe problem states that Nina had 78 treats, and each bag has 3 treats, then it asks the correct option regarding the number of bags.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
need help on my hw rip me

Answers
Answer:
pretty sure its the first one
Step-by-step explanation:
Answer:
x<6
Step-by-step explanation:
its an open dot. this means 6 isn't part of the inequality.
The expression 28 + 63 is equivalent to
1 91
2 5,7
3 6/7
4 13,7
Answers
Answer:
1) 91
Step-by-step explanation:
28 + 63 = 91
What is the contrapositive of the following conditional? If a number is divisible by 10, then it is divisible by 5.
Answers
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer: No because that is not always true.
Explanation:
I hope this helped!
<!> Brainliest is appreciated! <!>
- Zack Slocum
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
(help) what type of triangle is shown below

Answers
. The London Eye is a popular tourist attraction in London, England and is one of the largest Ferris Wheels in the world. It has a diameter of 135 meters and makes one revolution (counterclockwise) every 30 minutes. It is constructed so that the lowest part of the Eye reaches ground level, enabling passengers to simply walk on to, and off of, the ride. Find a sinsuoid which models the height h of the passenger above the ground in meters t minutes after they board the Eye at ground level.
Answers
Answer:
\(y=-67.5[cos(\frac{\pi}{15}t)-1]\)
Step-by-step explanation:
We can start solving this problem by doing a drawing of London Eye. (See attached picture).
From the picture, we can see that the tourists will start at the lowest point of the trajectory, which means we can make use of a -cos function. So the function will have the following shape:
\(y=-Acos(\omega t)+b\)
where:
A=amplitude
\(\omega\) = angular speed.
t= time (in minutes)
b= vertical shift.
In this case:
A= radius = 67.5 m
\(\omega=2\pi f\)
where the frequency is the number of revolutions it takes every minute, in this case:
\(f=\frac{1}{30} rev/min\)
so:
\(\omega=2\pi (\frac{1}{30})\)
\(\omega=\frac{\pi}{15} rad/min \)
and
b= radius, so
b=A
b=67.5m
so we can now build our equation:
\(y=-67.5cos(\frac{\pi}{15} t)+67.5\)
which can be factored to:
\(y=-67.5[cos(\frac{\pi}{15}t)-1]\)
You can see a graph of what the function looks like in the end on the attached picture.


The required sinusoidal equation is \(y = -67.5 (cos\dfrac{\pi t}{15} -1)\)
Given that,
It has a diameter of 135 meters and makes one revolution (counterclockwise) every 30 minutes.
It is constructed so that the lowest part of the Eye reaches ground level, enabling passengers to simply walk on to, and off of, the ride.
We have to find,
A sinusoidal which models the height h of the passenger above the ground in meters t minutes after they board the Eye at ground level.
According to the question,
The tourists will start at the lowest point of the trajectory, which means we can make use of a -cos function. So the function will have the following shape:
\(y = -Acos(wt) + b\)
Where, A=amplitude , \(\omega\) = angular speed, t= time (in minutes) , b= vertical shift.
Then,
\(Radius = \dfrac{diameter}{2}\\\\Radius = \dfrac{135}{2}\\\\Radius = 65.5m\)
The frequency is the number of revolutions it takes every minute is determined by the formula is,
\(\omega = 2\pi f\)
Where,
\(f = \dfrac{1}{30} revolution \ per \ minute\)
Then,
\(\omega = 2\pi \times \dfrac{1}{30}\\\\\omega = \dfrac{\pi }{15}\ radian \ per\ minute\)
Here, The sinusoidal equation can be written as;
\(y = -67.5cos\dfrac{\pi t}{15} + 67.5\\\\y = -67.5 (cos\dfrac{\pi t}{15} -1)\)
Hence, The required sinusoidal equation is \(y = -67.5 (cos\dfrac{\pi t}{15} -1)\)
To know more about Frequency click the link given below.
https://brainly.com/question/9661952
16
Select the correct answer.
Which of the following graphs shows the solution set for the inequality below?
Ix+21+7>10
OA HH
OB. H
5
1 0 1 2 3
0 1
2 3 4
10
5 6

Answers
The solution set includes all real numbers less than -5, and all real numbers greater than 1, but does not include -5 or 1 themselves.
Option D is the correct answer.
We have,
We need to isolate the absolute value |x + 2| on one side of the inequality.
We subtract 7 from both sides.
|x + 2| > 3
Next, we can split this inequality into two separate inequalities, one for when the expression inside the absolute value is positive, and one for when it is negative:
x + 2 > 3
or
- (x + 2) > 3
Solving for x in the first inequality.
x > 1
Solving for x in the second inequality.
-x - 2 > 3
Adding 2 to both sides and multiplying by -1.
x < -5
So the solution set for the inequality |x + 2| + 7 > 10 is the set of all x-values that satisfy either x > 1 or x < -5.
Using interval notation.
(-∞, -5) U (1, ∞)
Thus,
The solution set includes all real numbers less than -5, and all real numbers greater than 1, but does not include -5 or 1 themselves.
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ1
HELP Find the 29th term of the arithmetic sequence: -13, -6, 1, 8,...

Answers
Answer: so the answer is -9 + 23*7 = 152
Step-by-step explanation: a24 = a1 + (24-1)d where a1 = -9 and d = common difference ( 12-5 = 7)
Hope this helped :D
Ann said she was thinking of a number higher than Joe. Hal is thinking of double the number 5 and Ann is thinking of 5 to the 3rd power who is taking us a larger number. ExplainAnswer Explanation
Answers
About large or small numbers comparison
Answer 5^3 = 125
Explanation
Hal number is 2x5
Ann number is 5^3
Joe number is ?
5^3 = 25x 5 so
its 25/2 times bigger Ann number
Solve the system by any method you choose: .No solution exists.There are an infinite number of solutions.(0, –1)(1, 0)
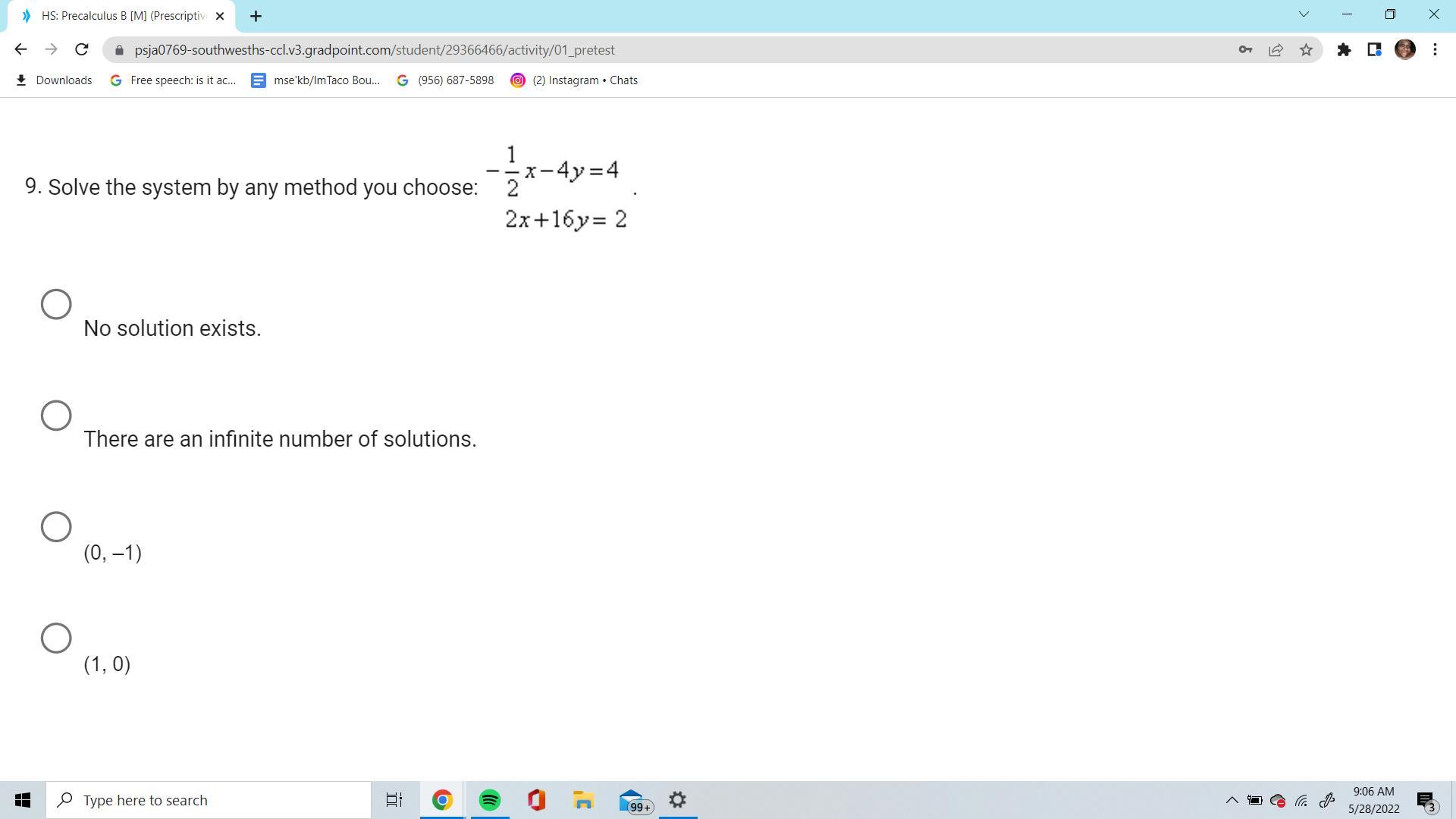
Answers
We are given the following system of equations
\(\begin{gathered} -\frac{1}{2}x-4y=4 \\ 2x+16y=2 \end{gathered}\)Let us solve the above system of equations using the elimination method.
Suppose we want to cancel the x terms, then we have to multiply eq.1 by 4.
\(4\cdot(-\frac{1}{2}x-4y=4)\Rightarrow-2x-16y=16\)Now, add the two equations
As you can see, after adding the equations we get 0 = 18 which cannot be true.
This means that no solution exists for this system of linear equations.
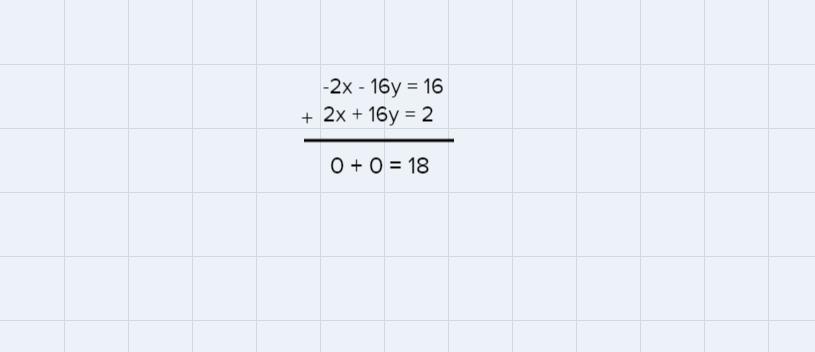
Help ASAP , 15 points and a brainy.

Answers
Answer:
B
Step-by-step explanation:
Answer:
I think the answer is B. It slopes downward from left to right.
13.1 divided by 1.6, answer quickly.
Answers
Answer:
8.1875
Step-by-step explanation:
which function will have the greatest value at
\(x = 16 \)
\( y = {10}^{16} \)
\(y = {x}^{2} - 17x + 182\)
\(y = {1.17}^{x} \)
Answers
The function that would have the greatest value at x = 16 include the following: B. y = x² - 17x + 182.
How to determine the corresponding output value for the given function?In Mathematics and Geometry, a function is a mathematical equation which defines and represents the relationship that exists between two or more variables such as an ordered pair in tables or relations.
In this exercise, we would determine the corresponding output value for this function of y based on the x-value (x = 16) in simplified form as follows;
\(y = 10^{16}\)
y = 10,000,000,000,000,000.
y = x² - 17x + 182
y = 16² - 17(16) + 182
y = 256 - 272 + 182
y = 166.
\(y = 1.17^x\\\\y = 1.17^{16}\)
y = 12.330304108137675851908392069373.
Read more on function here: brainly.com/question/10687170
#SPJ1
Evaluate each expression and match it with its correct value. 1.2|11| 2.4|1| 3.1|-2| 4.11|-4| 5.9|-9|

Answers
To find the absolute value of a number , subtract the negative sign.
l-2 l = 2
l 11 l = 11
l 1 l = 1
l -4 l = 4
l- 9 l = 9
Two gymnasts are running toward each other in a floor routine, and they plan to precisely time a flip to stay synchronized for the audience. The path of the gymnasts is
parabolic and modeled by the following equations, where y is the height of the flip and x is the time in seconds:
y = -(x-57 + 3
y = -3/x-3) + X + 1
To make sure the flip is in unison, after how many seconds should the flip occur?
O 2 seconds
O 3 seconds
© 4 seconds
O 5 seconds
Answers
Answer:it might be 3
Step-by-step explanation:
due to someone getting 5sec wrong me getting 2 wrong another post with only three stars said 4 so did leave it to 4 or 3.
A job fair was held at the Student Union. 25% of the students who attended received job offers. Of all of the students at the job fair, 40% were from the College of Business. Among these business students, 50% received job offers. Let J be the event that a student is offered a job. Let B be the event that the student is from the College of Business.
Requried:
a. Are events J and B independent? Why or why not?
b. Are events J and B mutually exclusive? Why or why not?
c. Joe, who is not a business student, attended the job fair. What is the probability that he received a job offer?
d. Another student, Samantha, received a job offer. What is the probability that she is a Business student?
Answers
Answer:
A) Both events are not independent.
B) Both events are not mutually exclusive
C) 8.33%
D) 80%
Step-by-step explanation:
A) Both events are not independent. This is because, If B occurs it means that it is very likely that J will occur as well.
B) Both events are not mutually exclusive. This is because it is possible for both events J and B to occur at the same time.
C) we want to find the probability that Joe who is not a business student will receive the job offer.
This is;
P(J|Not B) = P(J & Not B)/P(Not B)
Now,
P(J & Not B) = P(J) – (P(B) × P(J | B))
25% of the students who attended received job offers. Thus; P(J) = 0.25
40% were from the College of Business. Thus;
P(B) = 0.4
Among the business students, 50% received job offers. Thus;
P(J|B) = 0.5
Thus;
P(J & Not B) = 0.25 - (0.4 × 0.5)
P(J & Not B) = 0.25 - 0.2
P(J & Not B) = 0.05
Since P(B) = 0.4
Then, P(Not B) = 1 - 0.4 = 0.6
Thus;
P(J|Not B) = 0.05/0.6
P(J|Not B) = 0.0833 = 8.33%
D) This probability is represented by;
P(B | J) = P(B & J)/P(J)
P(B & J) = (P(B) × P(J | B)) = (0.4 × 0.5) = 0.2
P(B | J) = 0.2/0.25
P(B | J) = 0.8 = 80%
A company sells sneakers and has a revenue that can be represented by the function R(s) = 100s – s2, where s represents the number of pairs of sneakers sold. The sneaker company has a fixed cost of $2,000, and each pair of sneakers costs $25 to manufacture. Which of the following functions represents the profit P(s) of the sneaker company?
P(s) = – s2 + 125s – 2,000
P(s) = – s2 + 125s + 2,000
P(s) = – s2 + 75s – 2,000
P(s) = – s2 + 75s + 2,000
Answers
Using the concept of profit, it is found that the function is:
\(P(s) = -s^2 + 75s - 2000\)
Profit is revenue subtracted by cost, that is:
\(P(s) = R(s) - C(s)\)
The revenue function is:
\(R(s) = 100s - s^2\)
Fixed cost of $2,000 thus $25 for each sneaker, thus, the cost function is:
\(C(s) = 2000 + 25s\)
Then, the profit function is:
\(P(s) = R(s) - C(s)\)
\(P(s) = 100 - s^2 - (2000 + 25s)\)
\(P(s) = -s^2 + 75s - 2000\)
A similar problem is given at https://brainly.com/question/24373628
A sphere has a radius of 9 in, which means its volume is 972π in3. The sphere is dilated by 2⁄3. What is the volume of the new sphere?
Answers
Answer:
08-Oct-2009 — If a spherical balloon has a volume of 972 pi cubic centimeters, what is ... is 4.pi.r^2 (its area remember not volume) as 4/3.pi.r^3=972pi r=9 ... and it is good to know the squares of the next 10 numbers.
Answer:
I have this same question on my math test.
Since the radius is 9, the diameter is 18.
The shape is being dilated by 2/3, so the new radius is 6.
Volume formula: V = 4/3πr^3
So now we plug in the values.
V = 4/3 x π x (6)^3
V = 4/3 x π x 216
V = 288π
If the answers do not have the pi symbol present, then it has been multiplied into the answer.
288 x 3.14 = 904.32
The new volume of the sphere is 904.32 in^3
Someone please help me with this (look at the image above)

Answers
9514 1404 393
Answer:
a) base: 29.4377 cm
b) hypotenuse: 30.7827 cm
c) area: 132.470 cm²
d) perimeter: 69.2204 cm
Step-by-step explanation:
a) The mnemonic SOH CAH TOA reminds you that ...
Tan = Opposite/Adjacent
tan(17°) = (9 cm)/base
base = (9 cm)/tan(17°) = 29.4377 cm
__
b) The sine relation could be used in the same way to find the hypotenuse:
hypotenuse = (9 cm)/sin(17°) ≈ 30.7827 cm
However, we're instructed to use the Pythagorean theorem. So, we have ...
hypotenuse = √(base² +(9 cm)²) ≈ √(886.577 +81) cm ≈ 30.7827 cm
__
c) The area is half the product of the base and height:
A = 1/2bh
A = (1/2)(29.4377 cm)(9 cm) ≈ 132.470 cm²
__
d) The perimeter is the sum of side lengths:
P = base + hypotenuse + height
P = (29.4377 +30.7827 +9) cm = 69.2204 cm
A manufacturer has 576 square inches of material available to construct the 6 faces of a carton, which will be in the shape of a rectangular prism. To maximize the volume, the carton will have dimensions such that the length and width are each twice the height.
Answers
To maximize the volume, of the rectangular prism, the carton should have dimensions of approximately 10.74 inches (length), 10.74 inches (width), and 5.37 inches (height).
What is the dimension required to maximize the volume of the box?Assuming the height of the rectangular prism is h inches.
According to the given information, the length and width of the prism will be twice the height, which means the length is 2h inches and the width is also 2h inches.
The total surface area of the rectangular prism is given by the formula:
Surface Area = 2lw + 2lh + 2wh
Substituting the values, we have:
576 = 2(2h)(2h) + 2(2h)(h) + 2(2h)(h)
576 = 8h² + 4h² + 4h²
576 = 16h² + 4h²
576 = 20²
h² = 576/20
h² = 28.8
h = √28.8
h = 5.37
The height of the prism is approximately 5.37 inches.
The length and width will be twice the height, so the length is approximately 2 * 5.37 = 10.74 inches, and the width is also approximately 2 * 5.37 = 10.74 inches.
Learn more on maximizing volume here;
https://brainly.com/question/10373132
#SPJ4
Hexagon DEFGHI is translated on the coordinate plane below to create hexagon D′E′F′G′H′I′: Hexagon DEFGHI and Hexagon D prime E prime F prime G prime H prime I prime on the coordinate plane with ordered pairs at D 2, 5, at E 5, 5, at F 6, 3, at G 5, 1, at H 2, 1, at I 1, 3, at D prime negative 6, negative 2, at E prime negative 3, negative 2, at F prime negative 2, negative 4, at G prime negative 3, negative 6, at H prime negative 6, negative 6, at I prime negative 7, negative 4
Answers
Answer: To find the image of a figure under a translation, you need to apply the same translation to every point in the figure.
In this case, the image of hexagon DEFGHI is hexagon D′E′F′G′H′I′. To find the image of each point, you can apply the translation that maps point D to point D′.
For example, to find the image of point E under the translation, you can apply the same translation that maps point D to point D′:
Point D is located at (2, 5).
Point D′ is located at (-6, -2).
The translation that maps point D to point D′ is a translation 6 units to the left and 2 units down.
To find the image of point E under this translation, you can apply the same translation to point E:
Point E is located at (5, 5).
The image of point E is located at (5 - 6, 5 - 2) = (-1, 3).
You can follow the same process to find the images of the other points under the translation.
Alternatively, you can use the coordinates of point D and point D′ to find the translation vector that describes the translation. The translation vector is a displacement that describes the change in position of a point under the translation.
In this case, the translation vector is given by the displacement from point D to point D′:
Point D is located at (2, 5).
Point D′ is located at (-6, -2).
The translation vector is given by the displacement (-6 - 2, -2 - 5) = (-8, -7).
To find the image of any point under the translation, you can add the translation vector to the coordinates of the point. For example, to find the image of point E under the translation, you can add the translation vector to the coordinates of point E:
Point E is located at (5, 5).
The translation vector is (-8, -7).
The image of point E is located at (5 - 8, 5 - 7) = (-3, -2).
You can follow the same process to find the images of the other points under the translation.
Step-by-step explanation:
HELP 2 math questions 20 points


Answers
Answer:
4th option is the answer for first question.
4th option is the answee for second question.
Step-by-step explanation:
please mark me as a brainlist..
Eliza volunteers at a nearby aquarium where she tracks the migratory patterns of humpback whales from their feeding grounds to their breeding grounds. She recorded the distance traveled by the whales each day for a 7-day period at the start of their migration. Based on Eliza's data, about how long will it take the humpback whales to travel the 3,100 miles to their breeding grounds?
Answers
Answer:
Step-by-step explanation:
This is a very confusing, or otherwise incomplete question. The data Eliza recorded from her study at the aquarium is not given, and thus we wouldn't be able to peg a number as the time it took to travel 3100 miles by the whales.
There are lots of date missing, the total number of whales the distance each whale traveled and even, how long each traveled. These missing has essentially rendered the question unsolvable
Explain how to simplify 3y - 4 - 5y
Answers
Answer:
-2y - 4
Step-by-step explanation:
\(3y-4-5y\\\\3y-5y-4\\\\\boxed{-2y-4}\)
'3y' and '-5y' are like terms, so we combine them.
Hope this helps.
Divide
14 divided by 2/7
Answers
Answer:
49
Step-by-step explanation:
The numbers in 14 divided by 2/7 are labeled below:
14 = whole number
2 = numerator
7 = denominator
To make it a fraction form answer, you multiply the whole number by the denominator and make the result the new numerator. The old numerator becomes the new denominator:
\(\frac{14*7}{2}=\frac{98}{2}\)
Thus, the answer to 14 divided by 2/7 in fraction form is:
\(\frac{98}{2}\)
To make the answer to 14 divided by 2/7 in decimal form, you simply divide the numerator by the denominator from the fraction answer above:
98 / 2 = 49
The answer is rounded to the nearest two decimal points if necessary.
98/2 can be simplified to 49/1.
49/1 is an improper fraction and should be written as 49.
[RevyBreeze]
The division of 14 by 2/7 gives the quotient 49.
What is Division?The division is one of the four introductory fine operations, the other three being addition, deduction, and addition. In simple words, division can be defined as the splitting of a large group into lower groups similar that every group will have an equal number of particulars. It's an operation used for equal grouping and equal sharing in calculation.
We have to divide 14 by 2/7.
So, We have to multiply the fraction by reciprocate the number 2/7 to 7/2.
So, the division is
= 14 x 7/2
= 7 x 7
= 49.
Thus, the quotient is 49.
Learn more about Division here:
https://brainly.com/question/21416852
#SPJ2
135°
Solve for <2.
62 = [?]
45°
&2
86°
Enter
![135Solve for <2.62 = [?]45&286Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/C2BrfqTsi1RDIOT6UvZYPscTulgbihLi.png)
Answers
Answer:
\( \displaystyle \angle2 = {49}^{ \circ} \)
Step-by-step explanation:
remember that,
if a side of a triangle is extended then exterior angle so formed equal to the sum of the two opposite interior angles
thus our equation is
\( \displaystyle \angle2 + {86}^{ \circ} = {135}^{ \circ} \)
cancel out 86° from both sides:
\( \displaystyle \angle2 = {49}^{ \circ} \)
hence,
the measure of the missing angle is 49°
Answer:
Solution given'
<2+45+86=180°[sum of interior angle of a triangle]
<2=180-131
<2=49°
Find an equation for the perpendicular bisector of the line segment whose endpoints are (-7,8) and (-1,4).
can someone please answer this as soon as possible
Answers
Answer:
y = +3/2x + 12
Step-by-step explanation:
get slope
get midpoint
get b
1.
(-7,8) and (-1,4)
get slope
(y₂ - y₁) / (x₂ - x₁)
slope is -2/3
perpendicular slope is the negative reciprocal :
+3/2
y=mx + b
y=+3/2x + b
get midpoint :
(x₁ + x₂)/2, (y₁ + y₂)/2
(-4,6)
get b
y=mx + b
6=+3/2(-4) + b
6= -6+ b
b = 12
y = +3/2x + 12
Which inequality represents the phrase below? a number more than 72 A. x < 72 B. x > 72 C. x > 71 D. x = 72
Answers
Answer:
the answer is. C.i hope this helps sorry if im wrong
Help plz
The coordinates of point A on a grid are (−4, 3). Point A is reflected across the y-axis to obtain point B. The coordinates of point B are ( , 3). (1 point)
Blank 1:
Answers
Answer:
(4, 3)
Step-by-step explanation:
Since, A (-4, 3) is reflected across the y-axis to obtain point B.
Therefore, y coordinate remains the same, x coordinate flips over the y axis to be positive.
(-4,3) ==>> (4,3)