Find the missing dimension of the cylinder
Volume = 1696.5 m3
Height 15m
Answers
The missing dimension of the cylinder is the radius, which is approximately 6.01 meters.
To solve this problemBy rearranging the formula for a cylinder's volume, we can get the missing dimension.
The volume of a cylinder is given by the formula:
Volume = π *\(radius^2 * height\)
We can rearrange this formula to solve for the radius:
\(radius^2\) = Volume / (π * height)
Plugging in the values we know:
\(radius^2 = 1696.5 m^3 /\) (π * 15 m)
\(radius^2 = 1696.5 m^3 /\)\((3.14159 * 15 m)\)
\(radius^2\) ≈ \(36.1518 m^2\)
Taking the square root of both sides:
radius ≈ √\((36.1518 m^2)\)
radius ≈ 6.01 m
Therefore, the missing dimension of the cylinder is the radius, which is approximately 6.01 meters.
Learn more about radius here : brainly.com/question/24375372
#SPJ1
Related Questions
Find the value of x in the triangle shown below.
2
7
x

Answers
Answer:
\( {2}^{2} + {x}^{2} = {7}^{2} \\ {x}^{2} = 49 - 4 \\ x = \sqrt{45} \\ x = 6.708\)
Answer:
By using Pythagoras theorem we get
H²=p²+b²
7²=2²+x²
X²=7²-2²
X=√(49-4)=√45=3√5
Step-by-step explanation:
Layson, Jane
Mark has a key ring with 10 similar keys. There are 3 gym locker keys, 2 car keys, I door key, and 4 toolbox keys. If Mark selects one key without looking, what is the probability he
selects a car key or door key?
Answers
The probability that Mark selects a car key or door key from the key ring is 0.3 or 30%.
What is probability?
Probability is a measure of the likelihood or chance of an event occurring. It is a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. Probability is calculated by dividing the number of favorable outcomes by the total number of possible outcomes. Probability theory provides a framework for understanding random events and the laws of chance, and it is an important tool for modeling and simulating complex systems.
Calculating the probability that he selects a car key or door key :
In this context, we are asked to find the probability of Mark selecting a car key or door key from the key ring. To calculate this probability, we need to first determine the total number of keys on the key ring and then count the number of car keys and door keys.
Total number of keys = 10
Number of car keys = 2
Number of door keys = 1
The probability of selecting a car key or door key can be found by adding the probability of selecting a car key to the probability of selecting a door key. Since there is only one door key and two car keys, the probability of selecting a car key is higher, and we can simplify the calculation by finding the probability of selecting a car key and then adding the probability of selecting a door key that hasn't already been selected.
Probability of selecting a car key = 2/10 = 0.2
Probability of selecting a door key = 1/9 (since one key has already been selected) = 0.1111...
Therefore, the probability of Mark selecting a car key or door key from the key ring is 0.2 + 0.1111... ≈ 0.3 or 30%.
To know more about probability visit :
brainly.com/question/11034287
#SPJ1
A chord which passes through the centre is called · A. radius · B. diameter · C. arc · D. none
Answers
Answer:
It would be a diameter
Step-by-step explanation:
The diameter is also a chord.
Solve for x. Leave your answer in simplest radical form.
X
12 ft
16 ft
HELP ASAPPP

Answers
Answer:
x = 4√7
Step-by-step explanation:
You can use the pythagorean theorem which is a² + b² = c²
if you plug it in, it would be...
x² + 12² = 16²
x² + 144 = 256, subtract 144 to both sides
x² = 112, square root both sides to make x by itself.
x = 4√7
The diagram shows a rectangle. Its width is 3a, and its height is 5b. Write down an expression for the area of the rectangle. Simplify your answer.
Answers
Area of a rectangle = height × width
= 5b × 3a
= 15ab
using the graph shown below, identify the maximum and minimum values, the midline, the amplitude, the., and the rate constant

Answers
Answer:
maximum: 40minimum: -10midline: 15amplitude: 25rate constant: ??Step-by-step explanation:
The maximum value is the y-coordinate of the most extreme point in the positive direction. On this graph, it is 40.
The minimum value is the y-coordinate of the most extreme point in the negative direction. On this graph, it is -10.
The midline is the line halfway between the maximum and minimum. Its y-coordinate is the average of the maximum and minimum: (40-10)/2 = 15.
The amplitude is the difference between the maximum and the midline:
40 -15 = 25.
__
The term "rate constant" is used for many things, but is rarely seen as a descriptor of a sine function. For that, you'll need to consult your text or other reference material. (Google turns up kinetic rate constants, chemical reaction rate constants, and others—nothing related to sine functions.)
The usual descriptors are frequency or period. (Frequency is the reciprocal of period.) On this graph, the period of the function is 6 units, so the frequency is 1/6 cycles per unit.

points A(-1.5) and b(6) are marked on a number line. find the coordinate of point m if it is know that AM:md = 1:2
Answers
The coordinates of point m if it is known that am : md = 1 : 2 is (4/3, 5)
How to find the coordinates of point m?The given parameters are
A = (-1, 5)
B = (6, 5)
Ratio, m : n = 1 : 2
The coordinates of point m are calculated using
M = 1/(m + n) * (mx2 + nx1, my2 + ny1)
So, we have
M = 1/(1 + 2) * (1 * 6 + 2 * -1, 1 * 5 + 2 * 5)
Evaluate the sum of products
So, we have
M = 1/3 * (4, 15)
Evaluate the product
M = (4/3, 5)
Hence, the coordinates of point m if it is known that am : md = 1 : 2 is (4/3, 5)
Read more about line segment ratio at
https://brainly.com/question/17374569
#SPJ1
Which line quote from Old Major's speech reveals to us the core message of the Seven Commandments?
Answers
This line quote from Old Major's "Whatever goes upon two legs is an enemy. Whatever goes upon four legs, or has wings, is a friend." This line ratio reveals that animals should not oppress each other and should instead be united as friends.
This line from Old Major's speech in Animal Farm reveals the core message of the Seven Commandments: animals should not oppress each other and should instead be united as friends. This is made clear by the dichotomy between “two legs” and “four legs or has wings”, which represent humans and animals respectively. By stating that animals should not oppress those like them, Old Major is emphasizing the need for all animals to stick together and reject the oppression humans are able to inflict on them. The Seven Commandments that Old Major lays out are meant to be a guide for the animals to follow so that they can come together and fight against the oppressive human regime. The commandment “no animal shall oppress another” is useful in this respect, as it reinforces the idea that animals should be united and work together towards a common goal.
Learn more about quote here
https://brainly.com/question/29775308
#SPJ4
The difference of the same side interior angles of two parrelels lines is 50 degrees find all angles
Answers
Answer:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
Step-by-step explanation:
Angle 1: Same-side interior angle of Line 1
Angle 2: Same-side interior angle of Line 2
We know that the difference between the angles is 50 degrees. Since the angles are supplementary, we can write the equation:
Angle 1 + Angle 2 = 180
Now, we need to express the difference between the angles in terms of Angle 1 or Angle 2. We can choose either angle, so let's express it in terms of Angle 1:
Angle 1 - Angle 2 = 50
We can rewrite this equation as:
Angle 1 = 50 + Angle 2
Now substitute this expression for Angle 1 into the first equation:
(50 + Angle 2) + Angle 2 = 180
Combine like terms:
2Angle 2 + 50 = 180
Subtract 50 from both sides:
2Angle 2 = 130
Divide by 2:
Angle 2 = 65
Now substitute this value back into the equation for Angle 1:
Angle 1 = 50 + Angle 2
Angle 1 = 50 + 65
Angle 1 = 115
Therefore, the angles are as follows:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
The equation c = 4m represents how many ice cream cones (c) are sold within a certain number of minutes (m) at a certain ice cream shop. Determine the constant of proportionality.
Answers
The constant of proportionality is 4.
The equation c = 4m represents a proportional relationship between the number of ice cream cones sold (c) and the number of minutes (m) during which they are sold. The constant of proportionality is the factor by which m is multiplied to obtain c.
To find the constant of proportionality, we can divide both sides of the equation by m, yielding:
c/m = 4m/m
c/m = 4
This means that for every additional minute of time during which the ice cream is sold, the number of ice cream cones sold will increase by a factor of 4. Alternatively, we could say that each ice cream cone sold takes 1/4 of a minute, or 15 seconds, to sell.
Finding the constant of proportionality is important in understanding the relationship between two variables and can be useful for making predictions.
For such more questions on proportionality
https://brainly.com/question/1496357
#SPJ8
What is the Surface Area of this prism?
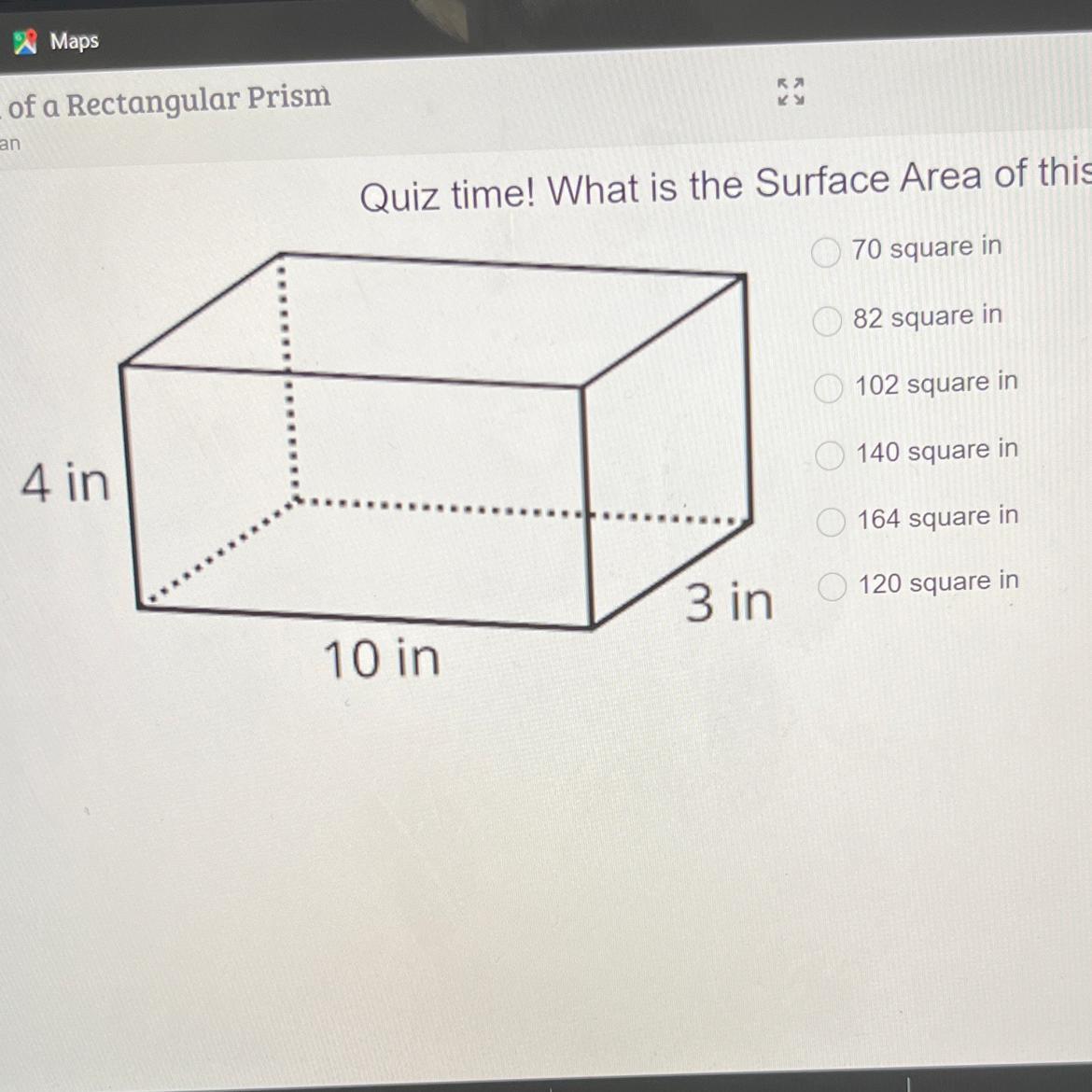
Answers
Answer:
164
Step-by-step explanation:
4 x 10 = 40
40 x 2 = 80 (there are two sides with the same measurements)
---
3 x 4 = 12
12 x 2 = 24 (there are two sides with the same measurements)
----
10 x 3 = 30
30 x 2 = 60 (there are two sides with the same measurements)
60 + 80 + 24 = 164
If x2 = 20, what is the value of x?
±square root of 10
±square root of 20
±10
±40
Answers
Answer:
± \(\sqrt{20}\)
Step-by-step explanation:
Given
x² = 20 ( take the square root of both sides )
x = ± \(\sqrt{20}\)
this is me and I am proud of my 15 year old self
Answers
Answer:
good
Step-by-step explanation:
thx for the points :)
If you are not a goofy ah please answer this

Answers
Answer:
72
Explanation:
First, we can find the top and bottom smaller squares of the rectangular prism. Since we are working with a variety of rectangles, we only need to use the equation L×W.
To start with, let's multiply 2×3, which gives us 6, the surface area of both the bottom and top rectangles, so now we need to multiply it by 2 to account for both of them. 6×2=12
Now, we'll find the surface area of the bigger rectangles in the middle, which are 6 by 3, so again we will need to multiply length times width, then by 2 to count both rectangles. 6×3=18×2=36
Finally, we can find the surface area of the smaller rectangles in the middle, which are 6 by 2. 6×2=12, then multiply by 2 since there are 2 of those rectangles, 12×2=24
Now to find the total surface area, we need to add the gathered surface area from each shape, 12+36+24=72
16ef³÷8e²f=
24m²n³
_____=
2mn
2k³+k
_____=
4k
Answers
Answer:
Answer is below
Step-by-step explanation:
16ef³÷8e²f=\(\frac{2f^{2}}{e}\)
\(\frac{24m^{2} n^{3} }{2mn} = 12m n^{2}\)
\(\frac{2k^{3} +k}{4k} =\frac{1}{2} k^{2} +\frac{1}{4}\)
Which graph best represents the solution set for this system of inequalities? y < − 1 /2 x − 1
Answers
Step-by-step explanation:0
The slope is 1/2, and the y-intercept is (0,-1).
The area shaded is what x could be

Determine the values of a and b, so that the following system of linear equations have infinitely many solutions:
(2a−1)x+3y−5=0
3x+(b−1)y−2=0
Answers
For the system of linear equations (2a−1)x+3y−5=0 and 3x+(b−1)y−2=0 to have infinitely many solutions, the two equations must be linearly dependent, meaning one equation can be obtained by multiplying the other equation by a constant. This can be achieved when the ratios of the coefficients of x, y, and constants in the two equations are equal, except for a scalar multiple. Therefore, setting (2a-1)/3 = -2/(b-1) = -5/2, we get a = -1/2 and b = 9.
To find the values of a and b such that the system of linear equations (2a−1)x+3y−5=0 and 3x+(b−1)y−2=0 has infinitely many solutions, we need to find the condition under which the two equations are linearly dependent.
If the two equations are linearly dependent, it means that one equation can be obtained by multiplying the other equation by a constant. Mathematically, this can be represented as:
k(2a−1)x + k(3y) − k(5) = 0 where k is a non-zero constant
and 3x + (b−1)y − 2 = 0
We can see that the coefficients of x and y in the two equations are 2a-1 and 3, and 3 and b-1, respectively. For the equations to be linearly dependent, the ratios of these coefficients must be equal, except for a scalar multiple. In other words:
(2a-1)/3 = (b-1)/(-2) = k where k is a non-zero constant
We can solve for k by setting any two ratios equal to each other. Let's set the first ratio equal to the second ratio:
(2a-1)/3 = (b-1)/(-2)
Cross-multiplying, we get:
-4a + 2 = 3b - 3
Simplifying, we get:
-4a + 3b = 5
Next, let's set the first ratio equal to the third ratio:
(2a-1)/3 = -5/2
Cross-multiplying, we get:
4a - 2 = -15
Simplifying, we get:
4a = -13
Solving for a, we get:
a = -13/4
Substituting this value of a into the equation -4a + 3b = 5, we get:
-4(-13/4) + 3b = 5
Simplifying, we get:
13 + 3b = 5
Solving for b, we get:
b = 9
Therefore, the values of a and b that make the system of linear equations (2a−1)x+3y−5=0 and 3x+(b−1)y−2=0 have infinitely many solutions are a = -1/2 and b = 9.
Learn more about linear equations:
https://brainly.com/question/11897796
#SPJ11
Considera el descuento indicado en cada tabla y calcula los diferentes porcentajes de descuento del mismo articulo
Answers
The 5% discount is 8.10, Namas divide 42 between the percentage follow me and give me crown.
A discount is a reduction in the price of a product or service offered to customers. It is a common marketing strategy used by businesses to attract customers and increase sales. Discounts can be offered in various forms, such as percentage off, dollar off, or buy-one-get-one-free deals.
Discounts are often used to clear out old inventory, promote new products or services, and to reward customer loyalty. They can be temporary or ongoing, and the amount of the discount can vary depending on the product, service, or promotion. Customers benefit from discounts as they can purchase products or services at a lower price, saving them money. Businesses benefit from discounts as they can increase sales volume, clear out inventory, and attract new customers.
To learn more about Discount visit here:
brainly.com/question/3541148
#SPJ4
Complete Question:-
Consider the discount indicated in each table and calculate the different discount percentages for the same item.

If you watch from ground level, a child riding on a merry-go-round will seem to be undergoing simple harmonic motion from side to side. Assume the merry-go-round is 10.6 feet across and the child completes 8 rotations in 120 seconds. Write a sine function that describes d, the child's apparent distance from the center of the merry-go-round, as a function of time t.
Answers
The sine function that describes the child's apparent distance from the center of the merry-go-round is d(t) = 5.3 sin(2π/15 * t)
How to write a sine function that describes the child's apparent distance?To write a sine function that describes the child's apparent distance from the center of the merry-go-round as a function of time t, we can start by finding the amplitude, period, and phase shift of the motion.
Amplitude:
The amplitude of the motion is half the diameter of the merry-go-round, which is 10.6/2 = 5.3 feet. This is because the child moves back and forth across the diameter of the merry-go-round.
Period:
The period of the motion is the time it takes for the child to complete one full cycle of back-and-forth motion, which is equal to the time it takes for the merry-go-round to complete one full rotation.
From the given information, the child completes 8 rotations in 120 seconds, so the period is T = 120/8 = 15 seconds.
Phase shift:
The phase shift of the motion is the amount of time by which the sine function is shifted horizontally (to the right or left).
In this case, the child starts at one end of the diameter and moves to the other end, so the sine function starts at its maximum value when t = 0. Thus, the phase shift is 0.
With these values, we can write the sine function that describes the child's apparent distance from the center of the merry-go-round as:
d(t) = 5.3 sin(2π/15 * t)
where d is the child's distance from the center of the merry-go-round in feet, and t is the time in seconds. The factor 2π/15 is the angular frequency of the motion, which is equal to 2π/T.
Learn more about sine function on:
https://brainly.com/question/30243373
#SPJ1
Carter can bake 11 cookies with each scoop of flour. With 4 scoops of flour, how many cookies can Carter bake?
Answers
Answer:
44 cookies
Step-by-step explanation:
1 scoop = 11 cookies
11 cookies * 4 scoops = 44 cookies
use multiples to determine the LCM of 45and 60
Answers
Answer:
LCM of 45 and 60: 180
Step-by-step explanation:
(Present value of an annuity) Determine the present value of an ordinary annuity of $4,500 per year for 16 years, assuming it earns 8 percent. Assume that the first cash flow from the annuity comes at the end of year 8 and the final payment at the end of year 23. That is, no payments are made on the annuity at the end of years 1 through 7 . Instead, annual payments are made at the end of years 8 through 23. The present value of the annuity at the end of year 7 is \$ (Round to the nearest cent.)
Answers
The present value of the annuity at the end of year 7 is approximately $47,069.08.
To calculate the present value of an ordinary annuity, we can use the formula:
PV = PMT * [(1 - (1 + r)⁻ⁿ) / r],
where PV is the present value, PMT is the annual payment, r is the interest rate per period, and n is the number of periods.
In this case, the annual payment is $4,500, the interest rate is 8%, and the number of periods is 16. However, the payments start at the end of year 8 and continue until the end of year 23, which means there is a delay of 7 years.
Using the formula, the present value at the end of year 7 can be calculated as:
PV = $4,500 * [(1 - (1 + 0.08)⁻¹⁶) / 0.08] = $47,069.08.
To know more about present value:
https://brainly.com/question/29140663
#SPJ4
What is the image point of (6, -7) after the transformation D4 T3,5?
Answers
The final image of the given points after the given translation and dilation of D4, T3,5 is (27, -23).
What is meant by the term transformation?Image transformations usually involve the modification of various bands of data, such as a single multispectral image either from a number of images acquired at different times of the same area (i.e. multitemporal image data). Image transformations, in either case, generate "new" images from a variety of sources that highlight specific features or characteristics of interest more effectively than the original input images.For the given image point of (6, -7) .
First there is a dilation of 4.
Thus,
Image = (6×4 , -7×4)
Image = (24, -28)
Now, there is translation of 3 units right on x axis and 5 unit upward on y axis; T3,5.
Image = (24 + 3, -28 + 5)
Image = (27, -23)
Thus, the final image of the given points after the given translation and dilation is (27, -23).
To know more about the transformation, here
https://brainly.com/question/25982490
#SPJ13
I need help please
Pre algebra
It’s due please

Answers
Answer:
Jk is parallel to LM
Step-by-step explanation:
Answer:
A
Step-by-step explanation: in translations the shape will stay the same unless dialations if you use transfer paper you can see it
Of KR = x + 7, KM = 3X - 5, and JL = 4X - 10 what are the values of X and JR
Answers
The value of x is 19 and JR is 33 units.
Parallelogram:A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure.
From the question, the information available from the question is:
KR = x + 7,
KM = 3X - 5, and
JL = 4X - 10
We have to find the values of X and JR.
We know that:
In a parallelogram, this one in particular:
KR = RM
JR = RL
Also, we know that:
KM = KR + RM, but since KR and RM are the same length, the equation will be:
KM = 2KR.
3x - 5 = 2(x + 7)
3x - 5 = 2x + 14
x = 19.
JL = 4x - 10
JL = 4(19) - 10
JL = 66
Knowing that JR = RL and JL is 66 units long, JR = RL = 33 units each.
Hence, The value of x is 19 and JR is 33 units.
Learn more about Parallelogram at:
https://brainly.com/question/28854514
#SPJ4

3 less than the quotient of a number y and 4
Expression:
When y = 20, the value of the expression is
Please help ASAP!!
Answers
Step-by-step explanation:
3 less than the quotient of a number y and 4
= y/4 - 3.
When y = 20, y/4 - 3 = 20/4 - 3 = 2.
Find : 5/22 + 3/7 + (-8/21) + (-6/11)
Answers
Answer:
-125/462.
Step-by-step explanation:
5/22 + 3/7 + (-8/21) + (-6/11)
= 5/22 - 6/11 + 3/7 - 8/21 The LCM of 11 and 22 is 22 and of 7 & 21= 21:
= 5/22 - 12/22 + 9/21 - 8/21
= 1/21 - 7/22 The LCM of 21 and 22 is 462:
= 22/462 - 147/462
= -125/462.
True or False: To solve literal equations, use the steps of multi-step equations.
Answers
the milti-step equations true
the average score of all golfers for a particular course has a mean of and a standard deviation of . suppose golfers played the course today. find the probability that the average score of the golfers exceeded .
Answers
The probability that the average score of the golfers exceeded 62 = 0.0228
Given the mean score of all golfers, μ = 72
and the Standard Deviation, σ = 4
Number of golf players, n = 64
We have to find the probability that the average score of the golfers exceed 73. i.e., x = 73
This follows the Normal Distribution.
Hence the z-score, Z = (x - μ)/(σ/√n)
= (73 - 72)√64/4
= 2
Probability that the average score of the golfers exceeded 73 = P(Z > 2)
= 0.0228 [from the z-tables]
The question is incomplete. Find the complete question below:
t\The average score of all golfers for a particular course has a mean of 72 and a standard deviation of 4. Suppose 64 golfers played the course today. Find the probability that the average score of the golfers exceeded 73 .
Learn more about z-score at https://brainly.com/question/25638875
#SPJ4
66 x 7guess the answer no cheating no calculator no asking parent nothing figure it out
Answers
Answer:
462
Step-by-step explanation:
6×7×10×6 is how you do it