Find the midpoint of A and B where A has coordinates (2, 3)
and B has coordinates (8,9).
y
10
9
8
7
6
5
4
3
2
1
X
O
1 2 3 4 5 6 7 8 9 10
Answers
Answer:
The mid-point of AB is (5,6)
Step-by-step explanation:
The mid-point of two points lies between the middle of two points or divides the line in two equal parts.
The formula for finding mid-point, M, is:
\(M(x,y) = (\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
Here (x1,y1) are the coordinates of first point and (x2,y2) are coordinates of second point.
Given
(2, 3) and (8,9)
Putting the values in the formula
\(M(x,y) =(\frac{2+8}{2} , \frac{3+9}{2})\\M = (\frac{10}{2}, \frac{12}{2})\\M = (5,6)\)
Hence,
The mid-point of AB is (5,6)
Related Questions
5+8(3+x) simplify the expression. Please show your work
Answers
Answer:
29+8x
Step-by-step explanation:
5+8(3+x)
5+24+8x - Open parentheses
29+8x - Add like terms
g(x) = 3x2 – 2x + 7 2x + 5 Find g(-1)
Answers
Answer:
2x+5= g(−1)=12
Step-by-step explanation:
Simplify is simple
The base of an ice cream cone has a radius of 4cm and the cones height is 12cm
Answers
Answer:
V=201.06
Step-by-step explanation:
V=πr2h
3=π·42·12
3≈201.06193
Roger wants to make a deposit into his savings account. He is depositing 2 checks, one for $125.62 and the other for
$532.50. He would like to receive $40.00 in cash after the deposit. Calculate the amount that he will be depositing into
his savings account.
a. $658.12
b. $618.12
C.
$743.74
d $698.12
Answers
Answer:
B
Step-by-step explanation:
Add $125.62 and $532.50 and then subtract 40 from the total
The amount that he will be depositing into his savings account is, $618.12
We know that;
The process of combining two or more numbers is called the Addition. The 4 main properties of addition are commutative, associative, distributive, and additive identity.
We have to given that;
Roger wants to make a deposit into his savings account. He is depositing 2 checks, one for $125.62 and the other for $532.50. He would like to receive $40.00 in cash after the deposit.
Hence, The amount that he will be depositing into his savings account is,
⇒ $125.62 + $532.50 - $40
⇒ $658.12 - $40
⇒ $618.12
Thus, The amount that he will be depositing into his savings account is, $618.12
Learn more about the addition visit:
https://brainly.com/question/25421984
#SPJ7
what is an approximate solution of the system of equations? y=-0.5x+4 y=1+2x1.25,3.42.25,3.43.4,2.253.4,1.25
Answers
Combining the two equations gives us
\(-0.5x+4=2x+1\)We add 0.5x to both sides and get
\(4=2.5x+1\)and subtracting 1 from both sides gives
\(2.5x=3\)And finally, dividing both sides by 2.5 gives
\(x=1.2\)Putting this value of x into y = 2x + 1 gives
\(y=2(1.2)+1\)\(y=3.4\)Hence our solution is
\(\textcolor{#FF7968}{(1.2,3.4)}\)If WXYZ is a rhombus with W(1,3) and Y(9,11), what must be an equation of in order for WXYZ to be a rhombus? Explain how you found your answer.
Answers
The requried equation of the diagonals for which WXYZ will be rhombus is y = -x + 12 and y = x + 12.
What is a rhombus?A rhombus is a parallelogram with all sides of equal length. This means that the diagonals of a rhombus bisect each other at right angles.
Let's first find the length of the diagonals of rhombus WXYZ using the distance formula:
WY = \(\sqrt{[(9-1)^2 + (11-3)^2]]}\) = 8√2
Since the diagonals of a rhombus bisect each other at right angles, we can use the midpoint formula to find the midpoint M of the diagonal WY:
Midpoint M = ((1+9)/2, (3+11)/2) = (5, 7)
The slope of the line passing through W and Y is:
slope WY = (11-3)/(9-1) = 8/8 = 1
Therefore, the slope of the line perpendicular to WY is -1/1 = -1.
Using the point-slope form with point M and slope -1, we get:
y - 7 = -1(x - 5)
y = -x + 12
So, the equation of the line passing through M with a slope perpendicular to the line passing through W and Y is y = x + 12 equation for XZ will be the same but the slope will be +1 so the equation is y = x + 1.
Learn more about rhombus here:
https://brainly.com/question/12665650
#SPJ1
A multiple regression model involves 5 independent variables and a sample of 10 data points. If we want to test the validity of the model at the 5% significance level, the critical value is:
Answers
Answer:
The critical value is 6.26.
Step-by-step explanation:
It is provided that there are 5 independent variables involved in a multiple regression model and the sample consist of 10 data points.
The critical value of F to test the significance of the model is:
\(\text{Critical Value}=F_{\alpha, (k, n-k-1)}\)
Here,
k = number of independent variables
n = number of observations.
Then the critical value is:
\(\text{Critical Value}=F_{\alpha, (k, n-k-1)}\)
\(=F_{\alpha, (5, 10-5-1)}\\=F_{0.05,(5, 4)}\\=6.2561\\\approx 6.26\)
*Use a F-table.
Thus, the critical value is 6.26.

Graph the equation using slope-intercept form (y=mx +b)
-3x + y = -2
Answers
both x-axis in the graph is before 5 or -5
SLOPE-INTERCEPT: y=3x-2
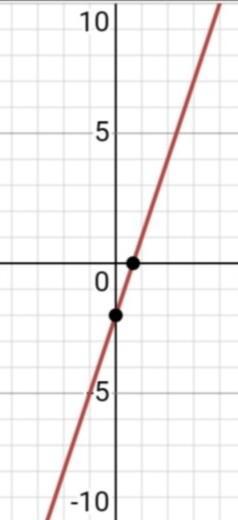

-3x+y=-2
y=3x-2

PLEASE HELP. What is a coterminal angle of 31pi over 6?

Answers
The coterminal angle of 31π/6 is angle of 210 degrees.
To find a coterminal angle, we can add or subtract a full revolution (2π) or any multiple of it.
Let's calculate the coterminal angle:
31π/6 = (30π/6) + (π/6) = 5π + π/6
To simplify the angle, we can express it in terms of a common denominator:
5π + π/6 -2π
3π+ π/6
19π/6
570 degrees.
The other coterminal angle is 210 degrees which lies in the third quadrant.
Therefore, the coterminal angle of 31π/6 is 210 degrees.
To learn more on trigonometry click:
https://brainly.com/question/25122835
#SPJ1
Tomas has two boxes to be shipped. One box weighs 3 \text{ kilograms}3 kilograms3, start text, space, k, i, l, o, g, r, a, m, s, end text. The other box weighs 720 \text{ grams}720 grams720, start text, space, g, r, a, m, s, end text.
Answers
Answer:
3.72kg
$29.76
See explanation below
Step-by-step explanation:
The question is incomplete as we are not told what we are to determine. Consider the following question
Question:
Tomas has two boxes to be shipped. One box weighs 3 kilograms. The other box weighs 720 grams.
a) What is the total weight of the boxes in kilogram?
b) If the shipping cost $8 per kilogram, what is the total cost of shipping.
Solution:
This is a question on measuring mass.
a) Total weight of the two boxes = weight of 1st box + weight of 2nd box
1st box = 3kg
2nd box = 720g
1000 g is equal to 1 kg
720g = (720/1000)kg = 0.72 kg
2nd box = 0.72 kg
Total weight of the two boxes = 3kg + 0.72kg
Total weight of the two boxes = 3.72kg
b) cost of shipping per kg = $8
cost of shipping for 3.72 kg = 8 × 3.72
Total cost of shipping for both boxes = $29.76
Answer: from my calculations its 3.72
which is also 3720 grams
Best answer gets brainliest!!!
Choose 3 plz!


Answers
I believe that the answer B,D,and E
Answer:
A, D, and E (I think)
Step-by-step explanation:
I'm pretty sure those would be the right answers, sorry that this isn't much of an explanation lol
What is the value of y?

Answers
Answer:
95°
Step-by-step explanation:
120° = 25° + y ( exterior angle of a triangle is equal to the sum of two opposite interior angles)
y = 120° - 25°
y = 95°
Hope it will help :)❤
Part 1: Write the equation of the graphed line in slope intercept (y= mx + b).

Answers
Answer:
1. y = 2x - 5
2. y = (-1/3)x
3. y = -4
4. y = (-3/4)x + 7
5. x = 6
6. y = -3x - 8
Step-by-step explanation:
1.
Point 1: (0, -5) Point 2: (-1, -7)
(x₁, y₁) (x₂, y₂)
y₂ - y₁ -7 - (-5) -7 + 5 -2
m = ------------ = ----------- = ---------- = ------ = 2
x₂ - x₁ -1 - 0 -1 -1
y - y₁ = m (x - x₁)
y - (-5) = 2(x - 0)
y + 5 = 2x - 0
-5 -5
y = 2x - 5
----------------------------------------------------------------------------------------------------------
2.
Point 1: (0, 0) Point 2: (3, -1)
(x₁, y₁) (x₂, y₂)
y₂ - y₁ -1 - 0 -1
m = ------------ = ----------- = ----------
x₂ - x₁ 3 - 0 3
y - y₁ = m (x - x₁)
y - (0) = (-1/3)(x - 0)
y - 0 = (-1/3)x - 0
-0 -0
y = (-1/3)x
----------------------------------------------------------------------------------------------------------
3.
Point 1: (0, -4) Point 2: (-5, -4)
(x₁, y₁) (x₂, y₂)
y₂ - y₁ -4 - (-4) -4 + 4 0
m = ------------ = ----------- = ---------- = ------ = 0
x₂ - x₁ -5 - 0 -5 -5
y = -4
----------------------------------------------------------------------------------------------------------
4.
Point 1: (0, 7) Point 2: (4, 4)
(x₁, y₁) (x₂, y₂)
y₂ - y₁ 4 - 7 -3
m = ------------ = ----------- = ----------
x₂ - x₁ 4 - 0 4
y - y₁ = m (x - x₁)
y - 7 = (-3/4)(x - 0)
y - 7 = (-3/4)x - 0
+7 +7
y = (-3/4)x + 7
----------------------------------------------------------------------------------------------------------
5.
Point 1: (6, 0) Point 2: (6, 3)
(x₁, y₁) (x₂, y₂)
y₂ - y₁ 3 - 0 3
m = ------------ = ----------- = ---------- = undefined
x₂ - x₁ 6 - 6 0
x = 6
----------------------------------------------------------------------------------------------------------
6.
Point 1: (0, -8) Point 2: (-4, 4)
(x₁, y₁) (x₂, y₂)
y₂ - y₁ 4 - (-8) 4 + 8 12
m = ------------ = ----------- = ---------- = ------ = -3
x₂ - x₁ -4 - 0 -4 -4
y - y₁ = m (x - x₁)
y - (-8) = -3(x - 0)
y + 8 = -3x - 0
-8 -8
y = -3x - 8
I hope this helps!
PLEASE HELP !! ILL GIVE BRAINLIEST !!

Answers
Answer:
jkh and ihk
Step-by-step explanation:
Answer:
<JHK and IHK
Step-by-step explanation:
3 A system of two linear equations is graphed on a coordinate plane. If the system of
equations has infinitely many solutions, which statement must be true?
a. On the graph, there are no points (x, y) that satisfy both equations.
b. On the graph, there is exactly one point (x, y) that satisfies both equations.
c. On the graph, any point (x, y) that satisfies one of the equations cannot satisfy the
other equation.
d.
On the graph, any point (x, y) that satisfies one of the equations must also satisfy
the other equation.
Answers
Answer:
d. On the graph, any point (x, y) that satisfies one of the equations must also satisfy the other equation.----------------------
If the system of linear equations has infinitely many solutions, it means the two lines overlap.
In other words, each point of one of the lines also belongs to the second line.
Choices a, b, c give us one or no solutions and therefore not the answer.
Choice d is reflecting the infinitely many solutions and hence is the correct one.
Mr. Pham is looking at renting a
vacation home.
He finds one that can be rented for $229 per night. In
addition, there iS a one-time cleaning fee of $89.
Write an equation that shows how the cost of renting the house, y, depends on the number of nights,
Do not include dollar signs in the equation.
Answers
89
+
3
×
229
Calculate the product or quotient:
89
+
687
Calculate the sum or difference:
776
get the result:
776
Answer: 776
The equation which represents the cost of renting the house, y, depends on the number of nights x is y = 229x + 89.
How to form an equation?Determine the known quantities and designate the unknown quantity as a variable while trying to set up or construct a linear equation to fit a real-world application.
As per the given,
Per night cost = $229 per night
Fixed cost (cleaning fee) = $89
Total cost = Fixed cost + per night cost × number of nights.
The total cost y for x number of nights will be,
y = 229 + 89x
y = 89x + 229
Hence "The equation which represents the cost of renting the house, y, depends on the number of nights x is y = 229x + 89".
For more about the equation,
https://brainly.com/question/10413253
#SPJ2
PLZ ANSWER WILL MARK BRAINLIEST

Answers
Answer:
I think the answer is C Angle-Angle-Side im not sure if im accurate but i hope it helps
Step-by-step explanation:
There are 15 pieces of fruit in a bowl and 6 of them are apples. What
percentage of the pieces of fruit in the bowl are apples?
O 0.06%
O 0.4%
O 6%
40%
Answers
Answer:
40%.
Step-by-step explanation:
There are 6 / 15 apples out of the bowl.
6/15 = 2/5 = 0.4
So, 40% of the fruit in the bowl are apples.
Hope this helps!
according to the graph, what is the value of the constant in the equation below?

Answers
Answer:
D . 0.4
Step-by-step explanation:
let the height be the y coordinate
let the width be the x coordinate
first point :
width/x : 0.5
height/y : 0.8
according to the formula given:
height = constant/width :
so:
0.8 = constant/0.5
constant = 0.4
next point:
x : 0.8
y : 0.5
0.5 = constant/0.8
constant = 0.4
for all of the points, the constant is 0.4
Let P(x) = -50x+20,000x-1,5000,000 represent the profit function for manufacturing a particular model of recreational
vehicle (RV) and x represent the number of RVS produced monthly. Use a compound inequality to state the range of the
number of RVs that need to be sold each month for the company to make a profit.
O 0
100
200
none of the answer choices
O 0
O 100

Answers
Among the given answer choices, the correct option that represents this range is "0 100 200 none of the answer choices".
To determine the range of the number of RVs that need to be sold each month for the company to make a profit, we need to consider the profit function and find the values of x that result in a positive profit.
The profit function is given by P(x) = -50x + 20,000x - 1,500,000.
To make a profit, the value of P(x) must be greater than zero (P(x) > 0). We can set up the inequality:
-50x + 20,000x - 1,500,000 > 0.
Combining like terms, we have:
19,950x - 1,500,000 > 0.
Now, let's solve this inequality for x:
19,950x > 1,500,000.
Dividing both sides by 19,950, we get:
x > 1,500,000 / 19,950.
Simplifying the right side, we have:
x > 75.
The range of the number of RVs that need to be sold each month for the company to make a profit is x > 75.
Among the given answer choices, the correct option that represents this range is "0 100 200 none of the answer choices".
for such more question on range
https://brainly.com/question/30389189
#SPJ8
Find the height of the tower using the information given in the illustration.

Answers
using SOH CAH TOA
Tan 85.144 =h/130
h=tan 85.144*130
h=1530.19 fr

I need Help please!!!

Answers
Step-by-step explanation:
it seems you solved the tricky part yourself already.
just to be sure, let's do the first derivative here again.
the easiest way would be for me to simply multiply the functional expression out and then do a simple derivative action ...
f(t) = (t² + 6t + 7)(3t² + 3) = 3t⁴ + 3t² + 18t³ + 18t + 21t² + 21 =
= 3t⁴ + 18t³ + 24t² + 18t + 21
f'(t) = 12t³ + 54t² + 48t + 18
and now comes the simple part (what was your problem here, don't you know how functions work ? then you are in a completely wrong class doing derivatives; for that you need to understand what functions are, and how they work). we calculate the function result of f'(2).
we simply put the input number (2) at every place of the input variable (t).
so,
f'(2) = 12×2³ + 54×2² + 48×2 + 18 = 96 + 216 + 96 + 18 =
= 426
Byron deposits 13,500 in an account that earns 2.6% interest compounded monthly. How many years will it take for Byron's money to double if he does not deposit or withdraw any funds during that time?
Answers
Answer:
About 27 years.
Step-by-step explanation:
Byron deposits $13,500 in an account that earns 2.6% interest compounded monthly, and we want to determine how many years it will take for Byron's money to double.
Recall that compound interest is given by the formula:
\(\displaystyle A = P\left( 1 + \frac{r}{n}\right)^{nt}\)
Since our initial deposit is $13,500 at a rate of 2.6% compounded monthly, P = 13500, r = 0.026, and n = 12:
\(\displaystyle \begin{aligned} A &= (13500)\left( 1 + \frac{(0.026)}{(12)}\right)^{(12)t} \\ \\ &=13500\left(\frac{6013}{6000}\right)^{12t} \end{aligned}\)
For his deposit to double, A must equal $27,000. Hence:
\(\displaystyle (27000) &=13500\left(\frac{6013}{6000}\right)^{12t}\)
Solve for t:
\(\displaystyle \begin{aligned} 27000 &= 13500 \left(\frac{6013}{6000}\right)^{12t} \\ \\ \left(\frac{6013}{6000}\right)^{12t} &= 2 \\ \\ \ln\left(\frac{6013}{6000}\right)^{12t} &= \ln (2)\\ \\ 12t \ln \frac{6013}{6000} &= \ln 2 \\ \\ t &= \frac{\ln 2}{12\ln \dfrac{6013}{6000}} = 26.6883... \approx 27\end{aligned}\)
In conclusion, it will take Byron about 27 years for his deposit to double.
A shop sells a particular of video recorder. Assuming that the weekly demand for the video recorder is a Poisson variable with the mean 3, find the probability that the shop sells. . (a) At least 3 in a week. (b) At most 7 in a week. (c) More than 20 in a month (4 weeks).
Answers
Answer:
a) 0.5768 = 57.68% probability that the shop sells at least 3 in a week.
b) 0.988 = 98.8% probability that the shop sells at most 7 in a week.
c) 0.0104 = 1.04% probability that the shop sells more than 20 in a month.
Step-by-step explanation:
For questions a and b, the Poisson distribution is used, while for question c, the normal approximation is used.
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:
\(P(X = x) = \frac{e^{-\lambda}*\lambda^{x}}{(x)!}\)
In which
x is the number of successes
e = 2.71828 is the Euler number
\(\lambda\) is the mean in the given interval.
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
The Poisson distribution can be approximated to the normal with \(\mu = \lambda, \sigma = \sqrt{\lambda}\), if \(\lambda>10\).
Poisson variable with the mean 3
This means that \(\lambda= 3\).
(a) At least 3 in a week.
This is \(P(X \geq 3)\). So
\(P(X \geq 3) = 1 - P(X < 3)\)
In which:
\(P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)\)
Then
\(P(X = x) = \frac{e^{-\lambda}*\lambda^{x}}{(x)!}\)
\(P(X = 0) = \frac{e^{-3}*3^{0}}{(0)!} = 0.0498\)
\(P(X = 1) = \frac{e^{-3}*3^{1}}{(1)!} = 0.1494\)
\(P(X = 2) = \frac{e^{-3}*3^{2}}{(2)!} = 0.2240\)
So
\(P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0498 + 0.1494 + 0.2240 = 0.4232\)
\(P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 1 - 0.4232 = 0.5768\)
0.5768 = 57.68% probability that the shop sells at least 3 in a week.
(b) At most 7 in a week.
This is:
\(P(X \leq 7) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7)\)
In which
\(P(X = x) = \frac{e^{-\lambda}*\lambda^{x}}{(x)!}\)
\(P(X = 0) = \frac{e^{-3}*3^{0}}{(0)!} = 0.0498\)
\(P(X = 1) = \frac{e^{-3}*3^{1}}{(1)!} = 0.1494\)
\(P(X = 2) = \frac{e^{-3}*3^{2}}{(2)!} = 0.2240\)
\(P(X = 3) = \frac{e^{-3}*3^{3}}{(3)!} = 0.2240\)
\(P(X = 4) = \frac{e^{-3}*3^{4}}{(4)!} = 0.1680\)
\(P(X = 5) = \frac{e^{-3}*3^{5}}{(5)!} = 0.1008\)
\(P(X = 6) = \frac{e^{-3}*3^{6}}{(6)!} = 0.0504\)
\(P(X = 7) = \frac{e^{-3}*3^{7}}{(7)!} = 0.0216\)
Then
\(P(X \leq 7) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 0.0498 + 0.1494 + 0.2240 + 0.2240 + 0.1680 + 0.1008 + 0.0504 + 0.0216 = 0.988\)
0.988 = 98.8% probability that the shop sells at most 7 in a week.
(c) More than 20 in a month (4 weeks).
4 weeks, so:
\(\mu = \lambda = 4(3) = 12\)
\(\sigma = \sqrt{\lambda} = \sqrt{12}\)
The probability, using continuity correction, is P(X > 20 + 0.5) = P(X > 20.5), which is 1 subtracted by the p-value of Z when X = 20.5.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{20 - 12}{\sqrt{12}}\)
\(Z = 2.31\)
\(Z = 2.31\) has a p-value of 0.9896.
1 - 0.9896 = 0.0104
0.0104 = 1.04% probability that the shop sells more than 20 in a month.
The probability of the selling the video recorders for considered cases are:
P(At least 3 in a week) = 0.5768 approximately.P(At most 7 in a week) = 0.9881 approximately.P( more than 20 in a month) = 0.0839 approximately.What are some of the properties of Poisson distribution?Let X ~ Pois(λ)
Then we have:
E(X) = λ = Var(X)
Since standard deviation is square root (positive) of variance,
Thus,
Standard deviation of X = \(\sqrt{\lambda}\)
Its probability function is given by
f(k; λ) = Pr(X = k) = \(\dfrac{\lambda^{k}e^{-\lambda}}{k!}\)
For this case, let we have:
X = the number of weekly demand of video recorder for the considered shop.
Then, by the given data, we have:
X ~ Pois(λ=3)
Evaluating each event's probability:
Case 1: At least 3 in a week.
\(P(X > 3) = 1- P(X \leq 2) = \sum_{i=0}^{2}P(X=i) = \sum_{i=0}^{2} \dfrac{3^ie^{-3}}{i!}\\\\P(X > 3) = 1 - e^{-3} \times \left( 1 + 3 + 9/2\right) \approx 1 - 0.4232 = 0.5768\)
Case 2: At most 7 in a week.
\(P(X \leq 7) = \sum_{i=0}^{7}P(X=i) = \sum_{i=0}^{7} \dfrac{3^ie^{-3}}{i!}\\\\P(X \leq 7) = e^{-3} \times \left( 1 + 3 + 9/2 + 27/6 + 81/24 + 243/120 + 729/720 + 2187/5040\right)\\\\P(X \leq 7) \approx 0.9881\)
Case 3: More than 20 in a month(4 weeks)
That means more than 5 in a week on average.
\(P(X > 5) = 1- P(X \leq 5) =\sum_{i=0}^{5}P(X=i) = \sum_{i=0}^{5} \dfrac{3^ie^{-3}}{i!}\\\\P(X > 5) = 1- e^{-3}( 1 + 3 + 9/2 + 27/6 + 81/24 + 243/120)\\\\P(X > 5) \approx 1 - 0.9161 \\ P(X > 5) \approx 0.0839\)
Thus, the probability of the selling the video recorders for considered cases are:
Learn more about poisson distribution here:
https://brainly.com/question/7879375
Find the missing length indicated

Answers
x = 65
Step-by-step explanation:
cos theta = 25/x
cos theta = x/169
25/x = x/169
x² = 169 x 25
x = 65
The missing length x = 65, using the Pythagoras Theorem.
What is the Pythagoras Theorem?
According to the Pythagoras Theorem, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.
How to solve the question?In the question, we are asked to find the value of x.
In the right triangle ABC, by Pythagoras' Theorem,
AC² + BC² = AB²,
or, x² + BC² = (144 + 25)²,
or, BC² = 169² - x² ... (i).
In the right triangle ACD, by Pythagoras Theorem,
AD² + DC² = AC²,
or, 25² + DC² = x²,
or, DC² = x² - 25² ... (ii).
In the right triangle BCD, by Pythagoras Theorem,
BD² + DC² = BC²,
or, 144² + x² - 25² = 169² - x² {Substituting BC² = 169² - x² from (i) and DC² = x² - 25² from (ii)},
or, x² + x² = 169² + 25² - 144² {Rearranging},
or, 2x² = 28561 + 625 - 20736,
or, 2x² = 8450,
or, x² = 4225,
or, x = √4225 = 65.
Thus, the missing length x = 65, using the Pythagoras Theorem.
Learn more about the Pythagoras Theorem at
https://brainly.com/question/231802
#SPJ2

Using a rating scale, Tekinarslan (2008) measured computer anxiety among university students who use the computer very often, often, sometimes, and seldom. Below are the results of the one-way ANOVA. Source of Variation SS df MS F Between groups 1,959.79 3 653.26 21.16* Within groups (error) 3,148.61 102 30.86 Total 5,108.41 105 (a) What are the values for N and k
Answers
Answer:
K = 4 ; N = 106
Step-by-step explanation:
Given the following :
Source of VARIATION - SS - df - - MS - - - - - F
Between groups - 1,959.79 - 3 - - 653.26 - 21.16*
Error - - - - - - - - 3,148.61 - - - - 102 - - 30.86
Total - - - - - - - - - - - 5,108.41 - 105
The degree of freedom between group (treatment) (DFT) is obtained using the formula ;
K - 1, where k = number of groups observed
DFT = K - 1 ; From the ANOVA table, DFT = 3
3 = K - 1
3 + 1 = K
K = 4
To obtain sample size (N) :
Degree of freedom of Error (DFE) is the difference between the sample size and the number of groups observed.
DFE = N - K ; From. The table DFE = 102 ; K = 4
102 = N - 4
102 + 4 = N
N = 106
American Vending supplies vended food to a large university. Because students often kick the machines out of anger and frustration, management has a constant repair problem. The machines break down in a mean of 3 hours with a standard deviation of 3 hours. One repair worker can service one machine in a mean of 2 hours with a standard deviation of 2 hours. Currently, TWO repair workers are hired. Average flow time (W) was calculated as 2.305 from the posted queueing template. --- Average down machines in the entire system (L) are ___.
Answers
Answer:
0.77
Step-by-step explanation:
From the information given:
The breakdown time (a)= 3 hours
The breakdown rate (λ) = 1/a = 1/3
Average flow time in the system (W) = 2.305 hours
For the entire system;
The average down machines L = Wλ
= 2.305 × (1/3)
= 0.77
B=(3,5,6,9) and C=(2,4,6,8) Find (A). A/B (B). B/C C. A/C (D). C/A
Answers
Answer:
The question isn't clear. Can you provide more information or context? What is A? Is it a set or a number? Without this information, I can't provide a meaningful answer.
Find the vertex of the graph of the function
f(x)= -2x^2-16x-34
Answer Choices:
-2,-4
-4,-2
3,5
5,3
Answers
Answer:
(-4,-2)
Step-by-step explanation:
Round 2484 to the nearest thousand
Answers
Answer: 2000
Step-by-step explanation: First, let's focus on the number 484. Let's always ask ourselves this: "Is this number (484 in our case) greater than 500?"
I say 500 because that's the number that we start to round up to the nearest thousandth. So, 484 is less than 500, telling us to round down.
So, therefore 2484 rounded to the nearest thousand is 2000. I hope this helped.