Answers
Related Questions
A wheel with a radius of 45.0 cm rolls without slipping (c) the
along a horizontal floor At time ty, the dot P painted
on the rim of the wheel is at the point of contact between the
wheel and the floor. At a later time tz, the wheel has rolle
through one-half of a revolution. What is the displacement of wheel
during this interval?
Answers
Therefore, the displacement of the wheel during this interval is approximately 141.372 cm.
To find the displacement of the wheel during this interval, we need to determine the distance traveled by a point on the rim of the wheel.
Given:
Radius of the wheel: 45.0 cm
The wheel rolls without slipping
The wheel rolls through one-half of a revolution
Since the wheel rolls without slipping, the distance traveled by a point on the rim of the wheel is equal to the circumference of the wheel for each complete revolution. Therefore, the distance traveled for one-half of a revolution is equal to half the circumference of the wheel.
The circumference of a circle can be calculated using the formula: C = 2πr, where r is the radius of the circle.
Using the given radius of the wheel, we can calculate the circumference:
C = 2π(45.0 cm) ≈ 2π(45.0) cm ≈ 282.743 cm (rounded to three decimal places)
Since the wheel rolls through one-half of a revolution, the displacement is equal to half the circumference of the wheel:
Displacement = 0.5 × 282.743 cm ≈ 141.372 cm (rounded to three decimal places)
To know more about displacement,
https://brainly.com/question/28523509
#SPJ11
The wheel's displacement is equal to the 282.6 cm that it has covered in its voyage.
To find the displacement of the wheel during this intervalWe must ascertain the wheel's distance traveled and the displacement's direction.
Since the wheel has completed one-half of a revolution, the distance it has gone is equal to half its circumference. The formula: can be used to determine a circle's circumference:
Circumference = 2 * π * radius
In this case, the radius of the wheel is 45.0 cm. Let's calculate the circumference:
Circumference = 2 * π * 45.0 cm
Circumference ≈ 2 * 3.14 * 45.0 cm
Circumference ≈ 282.6 cm
So, the distance traveled by the wheel is approximately 282.6 cm.
The wheel's displacement is the angular separation between its starting point, where it first makes contact with the ground, and its finishing point, where it stops after rolling through one-half of a rotation. The point of contact with the floor does not move since the wheel is moving without slipping.
Therefore, the wheel's displacement is equal to the 282.6 cm that it has covered in its voyage.
Learn more about radius here : brainly.com/question/12908707
#SPJ4
a microorganism measures 5 μm in length. its length in mm would be
Answers
The length of the microorganism that measure 5μm is equivalent to 0.005 mm
What is unit conversion?It is the transformation of a value expressed in one unit of measurement into an equivalent value expressed in another unit of measurement of the same nature.
To solve this problem the we have to convert the units with the given information.
1mm is equal to 1000 μm
5μm * (1 mm/1000μm) = (5*1) / 1000 = 5/1000 = 0.005 mm = 5x10^-3 mm
The length of the microorganism that measure 5μm is equivalent to 0.005 mm
Learn more about unit conversion at: brainly.com/question/141163
#SPJ4
a city worker inspected 200 homes in dairy city. during that inspection, 120 homes were found to violate one or more city codes. the city worker released a statement that 60% of dairy city's 3,000 homes are in violation of city codes. this is .
Answers
If the city worker released the statement that 60% of dairy city's 3,000 homes are in violation of city codes , then the City Worker's statement is an example of : (d) Statistical Inference .
The Statistical Inference involves making generalizations about a population based on a sample.
In this case, the city worker has taken a sample of 200 homes out of the total 3,000 homes in Dairy City, and based on that sample, the City Worker is making an inference about the proportion of homes in violation of city codes for the entire population of Dairy City.
The statement is not a census as a census would involve collecting data from every single unit in the population, in this case every single home in Dairy City.
The given question is incomplete , the complete question is
A city worker inspected 200 homes in dairy city. during that inspection, 120 homes were found to violate one or more city codes. the city worker released a statement that 60% of dairy city's 3,000 homes are in violation of city codes.
The City Worker's statement is an example of :
(a) Census
(b) An experiment
(c) Descriptive Statistics
(d) Statistical Inference
Learn more about Statistical Inference here
https://brainly.com/question/13752289
#SPJ4
what is the equation for the table y=ab^x

Answers
Answer:
It is the equation for the table y=ab^x (b>1,and b≠1)
Step-by-step explanation:
I’ll give brainiest

Answers
Answer:
3
Step-by-step explanation:
the answer
At a hockey game a vendor sold a combined total of 168 sodas and hotdogs. The number of sodas sold was two times the number of hotdogs sold. Find the number of sodas and the number of hotdogs sold.
Answers
Step-by-step explanation:
168/3 = 56
so 112 sodas
56 hotdogs
5. A fair coin is flipped 10 times. (a) What is the probability that there are an equal number of heads and tails
Answers
Answer:
you have a 50/50 chance to get equal number of heads & tails
A car travels 54 km in 43 minutes.
What is its average speed in km/h?
Give your answer rounded to 1 decimal place.
Answers
Answer:
75.35km/h
Step-by-step explanation:
Answer:
75.4
Step-by-step explanation:
11.
19.4
x 5.37
Estimate. I don’t need the answer immediately.
Answers
Answer:
Approximately 95
Step-by-step explanation:
19 x 5 = 95
the text reports the results of large surveys of american college graduates regarding their college experience. what was one result?
Answers
According to the text, one result of the large surveys conducted among American college graduates regarding their college experience was that a majority of them felt that their college education helped them develop critical thinking and problem-solving skills.
In fact, around 80% of the respondents agreed that their college experience had helped them develop such skills, which they found useful in their personal as well as professional lives.
This is an important finding, as critical thinking and problem-solving abilities are highly valued in today's job market and are often considered essential for career success.
Moreover, the results suggest that American colleges are doing a good job in imparting these skills to their students. However, these survey also revealed that there were differences in the level of satisfaction with college education across different demographic groups, such as gender and ethnicity.
These findings highlight the need for colleges to ensure that their educational programs are inclusive and accessible to all students, regardless of their background.
learn more about surveys here: brainly.com/question/17373064
#SPJ11
a local politician is concerned that a program for the homeless in the city is discriminating against blacks and other minorities. the following data were taken from a random sample of black and white homeless people. race black white received services yes 6 7 13 no 4 9 13 10 16 26 a. is there a statistically significant relationship between race and whether the person received services from the program? b. compute column and row percentages for the table to determine the pattern of the relationship. which group was more likely to receive services in the sample? interpret both the column and row percentages that you have obtained.
Answers
(a) There is no statistically significant relationship between race and receiving services from the program.
(b) Black homeless people were more likely to receive services (60%) than white homeless people (43.75%).
How to find the relationship between race and receiving services?a. To test whether there is a statistically significant relationship between race and whether the person received services from the program, we can use a chi-squared test of independence.
The null hypothesis is that there is no relationship between race and receiving services, and the alternative hypothesis is that there is a relationship.
Using a chi-squared calculator, we obtain a chi-squared statistic of 0.267 and a p-value of 0.605. Since the p-value is greater than the significance level of 0.05, we fail to reject the null hypothesis and conclude that there is no statistically significant relationship between race and receiving services from the program.
How to find more likely to receive services?b. To compute column and row percentages, we can first calculate the total number of black and white homeless people who received services and who did not receive services:
Black homeless people who received services: 6/10 = 60%Black homeless people who did not receive services: 4/10 = 40%White homeless people who received services: 7/16 = 43.75%White homeless people who did not receive services: 9/16 = 56.25%We can also calculate the percentage of all homeless people who received services or did not receive services, by adding up the numbers in each column:
Percentage of homeless people who received services: 13/26 = 50%Percentage of homeless people who did not receive services: 13/26 = 50%In the sample, black homeless people were more likely to receive services (60%) than white homeless people (43.75%).
Learn more about statistically significant
brainly.com/question/29663617
#SPJ11
Find x:
(Round the answer to the nearest tenth if there is a decimal)
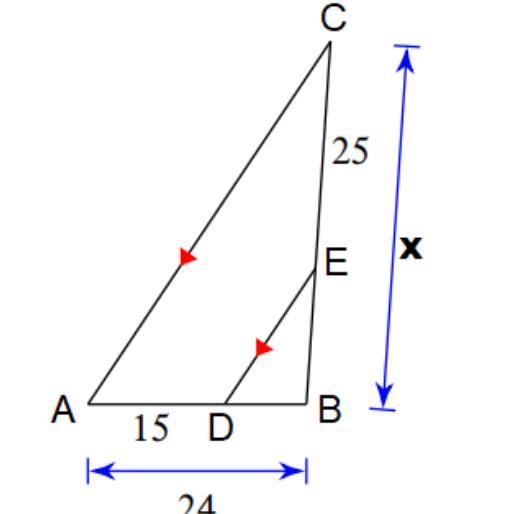
Answers
Answer:Angle x is congruent with the interior angle opposite side 8 (alternate interior angles)
Use tangent:
tan x = 8/15
x = arctan (8/15)
x = 28.1° (rounded)
Step-by-step explanation:
Factor each polynomial.
x²+5 x+4
Answers
The polynomial x² + 5x + 4 can be factored as (x + 1)(x + 4).
To factor the polynomial x² + 5x + 4, we need to determine two binomials whose product equals the original polynomial. We look for two factors that, when multiplied together, result in the given quadratic expression.
In this case, we consider the coefficient of x², which is 1. We know that the factors will have the form (x + a)(x + b), where 'a' and 'b' are the constants we need to determine. We then look for values of 'a' and 'b' such that their sum equals the coefficient of x, which is 5 in this case, and their product equals the constant term, which is 4.
After some trial and error or by applying factoring techniques, we find that 'a' = 1 and 'b' = 4 satisfy these conditions. Therefore, we can express the polynomial x² + 5x + 4 as the product of the binomials (x + 1)(x + 4).
To verify the factorization, we can multiply (x + 1)(x + 4) using the distributive property:
(x + 1)(x + 4) = x(x) + x(4) + 1(x) + 1(4) = x² + 4x + x + 4 = x² + 5x + 4.
Thus, we have successfully factored the polynomial x² + 5x + 4 as (x + 1)(x + 4).
Learn more about polynomial here :
brainly.com/question/11536910?
#SPJ11
The data are the ages that collected from a neighborhood 30, 35, 8, 12, 48, 70, 50, 62, 78 Find the mean, variation, standard deviation, first quartile, median, third quartile and 65% percentile.
Answers
According to the question, the mean, variation, standard deviation, quartiles, median, and percentile for the given data set are:
Mean = 43.33
Variation = 9646.22
Standard Deviation = 98.21
First Quartile (Q1) = 12
Median = 48
Third Quartile (Q3) = 70
65th Percentile = 50
To find the mean, variation, standard deviation, quartiles, median, and percentile for the given data set, we can follow these steps:
Step 1: Sort the data in ascending order: 8, 12, 30, 35, 48, 50, 62, 70, 78.
Step 2: Calculate the mean:
\(Mean = \frac{8 + 12 + 30 + 35 + 48 + 50 + 62 + 70 + 78}{9} = 43.33\) (rounded to two decimal places).
Step 3: Calculate the variation:
\(\text{Variation} = \frac{{\sum((x_i - \text{mean})^2)}}{n}\\\\= \frac{{((8 - 43.33)^2 + (12 - 43.33)^2 + \ldots + (78 - 43.33)^2)}}{9}\\\\= 9646.22 \quad\)
Step 4: Calculate the standard deviation:
Standard Deviation = \(\sqrt{(Variation)} = \sqrt{(9646.22)} = 98.21\) (rounded to two decimal places).
Step 5: Calculate the quartiles:
First Quartile (Q1) = 12 (since it is the median of the lower half of the data).
Third Quartile (Q3) = 70 (since it is the median of the upper half of the data).
Step 6: Calculate the median:
The median is the middle value of the sorted data set, which is 48.
Step 7: Calculate the percentile:
To find the 65th percentile, we need to determine the value that separates the lowest 65% of the data from the highest 35%. Since the data set has 9 elements, 65% of 9 is 5.85. Rounding up, we get 6. The 6th element in the sorted data set is 50, which represents the 65th percentile.
Hence, the mean, variation, standard deviation, quartiles, median, and percentile for the given data set can be represented in LaTeX as follows:
\(\text{Mean} &= 43.33 \\\text{Variation} &= 9646.22 \\\text{Standard Deviation} &= 98.21 \\\text{First Quartile (Q1)} &= 12 \\\text{Median} &= 48 \\\text{Third Quartile (Q3)} &= 70 \\\text{65th Percentile} &= 50 \\\)
To know more about Standard Deviation visit-
brainly.com/question/29115611
#SPJ11
triangle ABC has the following verticles A (-4,6)B (6,6)C( 1,-3) is triangle ABC an equilateral traingle and why?
Answers
we know that
An equilateral truangle has three equal length sides
so
If triangle ABC is an equilateral triangle
then
AB=BC=AC
so
step 1
Find out the distance AB
The formula to calculate the distance between two points is equal to
\(d=\sqrt{(y2-y1)^2+(x2-x1)^2}\)we have
A (-4,6)
B (6,6)
substitue in the formula
\(\begin{gathered} d=\sqrt{(6-6)^2+(6+4)^2} \\ d=\sqrt{(0)^2+(10)^2} \\ dAB=10\text{ units} \end{gathered}\)step 2
Find the distance BC
we have
B (6,6)
C( 1,-3)
substitute the values in the formula
\(\begin{gathered} d=\sqrt{(-3-6)^2+(1-6)^2} \\ d=\sqrt{(-9)^2+(-5)^2} \\ d=\sqrt{81+25} \\ dBC=\sqrt{106\text{ units}} \end{gathered}\)we have that
AB is not equal to BC
therefore
Is not an equilateral triangle
Is not necessary calculate the distance AC
Consider the differential equation dy/dx = y^2 (2x + 2). Let y = f (x) be the particular solution to the differential equation with initial condition f(0) = -1.(a) find lim\frac{f(x)+1}{sinx}Show the work that leads to your answer.(b) Use Euler's method, starting at x = 0 with two steps of equal size, to approximate f(1/2).(c) find y = f (x), the particular solution to the differential equation with initial condition f(0) = -1
Answers
The limit of (f(x) + 1) / sin(x) as x approaches 0 is 0, the approximation for f(1/2) using Euler's method with two steps is 19/32 and the particular solution to the differential equation with the initial condition f(0) = -1 is: y(x) = -1 / (x² + 2x + 1) - 1.
(a) To find the limit of (f(x) + 1) / sin(x) as x approaches 0, we can first rewrite the given differential equation as:
dy / dx = y² (2x + 2)
Separating variables, we get:
dy / y² = (2x + 2) dx
Integrating both sides, we have:
∫(1 / y² ) dy = ∫(2x + 2) dx
Integrating the left side gives:
-1 / y = x² + 2x + C1
where C1 is the constant of integration.
Since we have the initial condition f(0) = -1, we substitute x = 0 and y = -1 into the above equation:
-1 / (-1) = 0² + 2(0) + C1
1 = C1
So the particular solution is:
-1 / y = x² + 2x + 1
Multiplying through by y gives:
-1 = y(x² + 2x + 1)
Simplifying further:
y(x² + 2x + 1) + 1 = 0
Now, to find the limit (f(x) + 1) / sin(x) as x approaches 0, we substitute x = 0 into the particular solution equation:
f(0)(0² + 2(0) + 1) + 1 = 0
-1(0) + 1 = 0
1 = 0
Therefore, the limit of (f(x) + 1) / sin(x) as x approaches 0 is 0.
(b) Using Euler's method, we approximate the value of f(1/2) starting at x = 0 with two steps of equal size. Let's choose the step size h = 1/4.
First step:
x0 = 0, y0 = f(0) = -1
Using the differential equation, we have:
dy / dx = y² (2x + 2)
dy = y² (2x + 2) dx
Approximating the derivative using the Euler's method:
Δy ≈ y² (2x + 2) Δx
Δy ≈ (-1)² (2(0) + 2) (1/4)
Δy ≈ 1/2
Next, we update the values:
x1 = x0 + Δx = 0 + 1/4 = 1/4
y1 = y0 + Δy = -1 + 1/2 = 1/2
Second step:
x0 = 1/4, y0 = 1/2
Using the differential equation again:
dy / dx = y^2 (2x + 2)
dy = y² (2x + 2) dx
Approximating the derivative using the Euler's method:
Δy ≈ y² (2x + 2) Δx
Δy ≈ (1/2)² (2(1/4) + 2) (1/4)
Δy ≈ 3/32
Updating the values:
x2 = x1 + Δx = 1/4 + 1/4 = 1/2
y2 = y1 + Δy = 1/2 + 3/32 = 19/32
Therefore, the approximation for f(1/2) using Euler's method with two steps is 19/32.
c)To find the particular solution to the differential equation dy/dx = y^2 (2x + 2) with the initial condition f(0) = -1, we can solve the separable differential equation.
Separating variables, we have:
dy / y² = (2x + 2) dx
Integrating both sides:
∫(1 / y² ) dy = ∫(2x + 2) dx
Integrating the left side:
-1 / y = x² + 2x + C
where C is the constant of integration.
To find the particular solution, we substitute the initial condition f(0) = -1:
-1 / (-1) = 0² + 2(0) + C
1 = C
So the particular solution is:
-1 / y = x² + 2x + 1
Multiplying through by y gives:
-1 = y(x² + 2x + 1)
Simplifying further:
y(x² + 2x + 1) + 1 = 0
Therefore, the particular solution to the differential equation with the initial condition f(0) = -1 is: y(x) = -1 / (x² + 2x + 1) - 1
To know more about differential check the below link:
https://brainly.com/question/28099315
#SPJ4
The perimeter of the scalene triangle is 54.6 cm. Which equation can be used to find the value of b if side a measures 8.7 cm?
Answers
A scalene triangle is a triangle that has 3 sides that are all different lengths.
Let these letters represent the problem:
a = 8.7
b = side 2
c = side 3
P = 54.6
To find the perimeter, we just need to add all the sides [ P = a + b + c ]
So, put what we have in the formula above.
54.6 = 8.7 + b + c
Best of Luck!
Answer:
17.4 + b= 54.6
Step-by-step explanation:
Whats 2 + 6? If the 2 is really a 7?
Answers
Answer:
13
Step-by-step explanation:
7 + 6 = 13
Solve x(−2)3=−2(5). The solution is x=
Answers
decimal form : 1.6 repeating
mixed number form : 1 2/3
trish buys a 36 pack of toilet paper rolls for $15 how much did she pay for 1 roll of toilet paper
Answers
Answer:
Step-by-step explanation:
So assuming that all the toilet paper rolls cost the same amount we need to find the unit rate. To find the unit rate it's a lot easier than teachers explain it. You just divide the first number by the second number and bam. 36/15 is 2.4. Trish payed 2 dollars and 40 cents for one toilet paper roll.
Suppose you invest $ 500 in a savings account that pays 3.5 % annual interest. How much will be in the account after five years?
Answers
Amount $593.84 will be in the account after five years.
According to the question we have been given that the
amount invested initially = $500
annual interest rate = 0.035
Time = 5 years.
The formula for the future value is given as
\(FV = a(1 + r)^{t}\) (1)
where , FV = future value
a = amount invested initially
r = annual interest rate
t = time
putting the required values in equation (1) we get
\(FV = 500 (1 + 0.035)^{5} \\FV = 500 ( 1.035)^{5}\)
FV = 500*1.188
FV = $ 593.84
Thus, $593.84 will be the amount in the account after five years.
Learn more about future value here : https://brainly.com/question/24703884
#SPJ4
I need help with these questions because I don't understand it.

Answers
Evaluating the given expressions and inequalities, we have;
\(11) \: \frac{x}{4} \cdot \left(2 + y - x \right) = 4\)
12) (8•a - 5•b) - 2•(a + b) = 4
\( 13) \: \frac{p \cdot (p + {a}^{2} )}{6} = 55 \)
\( 14) \: 3\cdot m - \frac{2\cdot m}{2} +\frac{n}{3} = 12 \)
\( 16) \: x \geq 11\frac{2}{3} \)
17) k > 9
18) v > 9
20) m ≤ 16
Which method can be used to evaluate the expressions and inequalities?The given expressions are;
\(11) \: \frac{x}{4} \cdot \left(2 + y - x \right)\)
Where x = 4, and y = 6, we have;
\(\frac{x}{4} \cdot \left(2 + y - x \right) = \frac{4}{4} \cdot \left(2 + 6 - 4 \right) = 4\)
Therefore;
\(\frac{x}{4} \cdot \left(2 + y - x \right) = 4\)
12) (8•a - 5•b) - 2•(a + b)
Where a = 3 and b = 2, we have;
(8•a - 5•b) - 2•(a + b) = (8×3 - 5×2) - 2•(3 + 2) = 4
Therefore;
(8•a - 5•b) - 2•(a + b) = 4\(13) \: \mathbf{\frac{p \cdot (p + {a}^{2} )}{6}} \)
Where a = 7, and p = 6, we have;
\( \frac{p \cdot (p + {a}^{2} )}{6} = \mathbf{ \frac{6 \times (6 + {7}^{2} )}{6}} = 55 \)
Therefore;
\( \frac{p \cdot (p + {a}^{2} )}{6} = 55 \)
\(14) \: \mathbf{3\cdot m - \frac{2\cdot m}{2} +\frac{n}{3} } \)
Where m = 5, and n = 6, we have;
\( 3\cdot m - \frac{2\cdot m}{2} +\frac{n}{3} = \mathbf{3\times 5 - \frac{2\times 5}{2} +\frac{6}{3} }= 12 \)
Therefore;
\( 3\cdot m - \frac{2\cdot m}{2} +\frac{n}{3} = 12 \)
\(16) \: \mathbf{1 \frac{1}{6} }\leq \frac{x}{10} \)
Which gives;
\( \frac{7}{6} \times 10 \leq x \)
\( \mathbf{ \frac{35}{3} }\leq x \)
\( x \geq 11\frac{2}{3} \)
17) 20 < k + 11
Therefore;
k > 20 - 11 = 9
k > 918) 6•v > 54
v > 54 ÷ 6 = 9
Therefore;
v > 9\(20) \: 8 \geq \mathbf{ \frac{m}{2}} \)
Therefore;
2 × 8 = 16 ≥ m
Which gives;
m ≤ 16Learn more about expressions and inequalities here:
https://brainly.com/question/8288444
https://brainly.com/question/11970438
#SPJ1
The line located opposite the prime meridian at 180 longitude is the blank
Answers
Answer: International Date Line
Maria spends $22 dollars on lottery tickets every week. shen also spends $133 per month on food. On an (annual) basis ,the money spent on lottery tickets is what percent of the money spent to buy food?
Answers
Maria spends $22 on lottery tickets every week and $133 every month on food yearly
This means that in a year
there are 52 weeks and she spends 22 x 52 = $1,144 on Lottery tickets
and there are 12 months in a year, so she spends 133 x 12 = $1,596 on food
The money spent to buy lottery tickets in relation to the money spent on food yearly in percentage is
\(\begin{gathered} \frac{1144}{1596}\times100 \\ =71.68\text{ percent approximately} \end{gathered}\)Enter the value that belongs in the
green box

Answers
Answer:
100
Step-by-step explanation:
Just add
CD bisects ∠ACB. Which statements must be true? Check all that apply.
1. AD = BD
2. AC = CD
3. m∠ACD = m∠BCD
4. m∠CDA = m∠CDB
5. m∠DCA = m∠DAC

Answers
Answer: A, C, D
Step-by-step explanation:
1) AD=BD must be true because the angle bisector drawn from the vertex angle of an isosceles triangle is the perpendicular bisector of the base.
2) AC=CD does not need to be true because angles ADC and CAD do not need to be congruent.
3) This must be true by the definition of an angle bisector.
4) This must be true because angles CDA and CDB are both right angles.
5) This does not need to be true because triangle ADC does not need to be isosceles.
help me graph y = 4x + 1
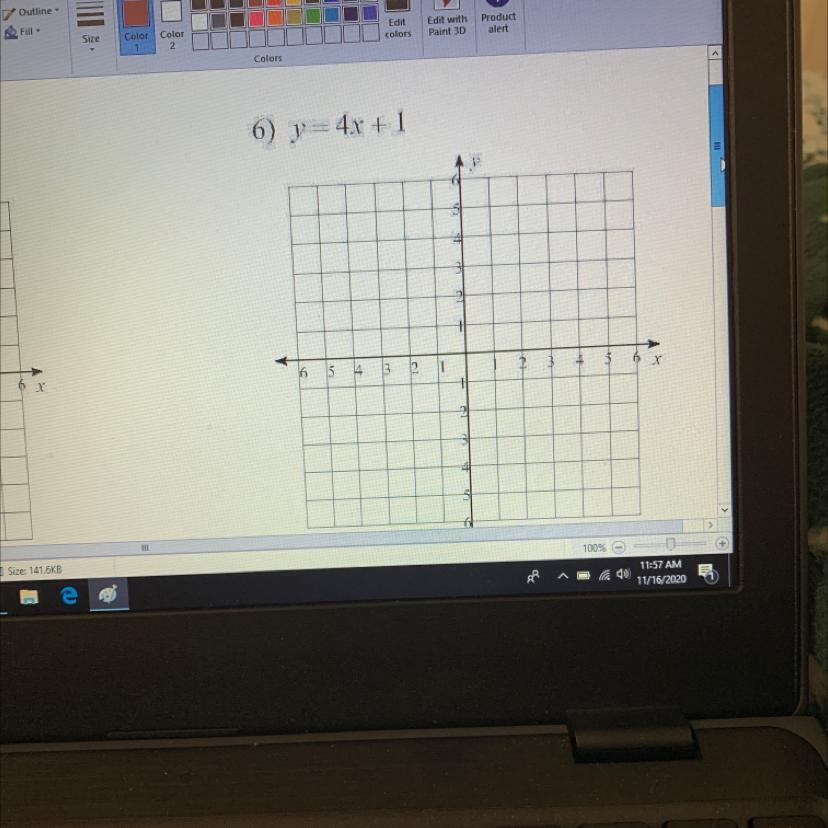
Answers
Please can someone help me

Answers
Answer:
706.86 cm
Step-by-step explanation:
=4pi(r^2)
=12.56(r^2)
=12.56(7.5^2)
=12.56(56.25)
=706.86
2/5
of an hour (in minutes)?
Answers
To convert hour into minute: (No. of hour × 60) minutes
So, 2/5 hours = (2/5 × 60) minutes = (120/5) minutes = 24 minutes
2\5 is 0.4 so 0.4 multiplied by 60 u get 24 so the answer is 24 minutes
8. Set up the artificial variable LP (Phase I LP) and specify the EBV and the LBV. DO not perform a complete pivot (complete with the exchange of basic variables). ( 16pts ) MaxZ=4x
1
+7x
2
+x
3
s.t.
2x
1
+3x
2
+x
3
=20
3x
1
+4x
2
+x
3
≤40
8x
1
+5x
2
+2x
3
≥70
x
1
,x
2
≥0
Answers
To set up the artificial variable LP (Phase I LP) for the given problem, we introduce an artificial variable, LP, to the objective function with a coefficient of 1. The artificial variable is used to identify infeasible solutions.
To set up the artificial variable LP (Phase I LP), we modify the objective function as follows:
Maximize Z = 4x1 + 7x2 + x3 + LP
The artificial variable LP is introduced to the objective function with a coefficient of 1. This allows us to track its value during the iterations.
The initial constraints remain the same:
2x1 + 3x2 + x3 = 20
3x1 + 4x2 + x3 + x4 = 40
8x1 + 5x2 + 2x3 - x5 = 70
The initial basic variables (BV) are the slack variables corresponding to the equality and inequality constraints, namely, x3 and x4. The artificial variable LP is initially a non-basic variable.
The initial artificial variables' basic variable (BVB) values are set to the right-hand side values of the constraints:
x3 = 20
x4 = 40
The initial artificial variable LP's value is set to 0.
Next, the artificial variable LP is selected as the entering variable, as it has a positive coefficient in the objective function. To determine the leaving variable, we perform the ratio test using the ratios of the right-hand side values and the entering column values (coefficients of LP) for the respective constraints.
The leaving variable is determined based on the minimum ratio, ensuring that the corresponding row represents a valid pivot element. If no valid pivot element is found, the problem is infeasible.
This completes the setup of the artificial variable LP (Phase I LP) without performing a complete pivot. Further steps would involve applying the simplex method and iteratively pivoting to find the optimal solution or identify infeasibility.
Learn more about coefficient here: brainly.com/question/13431100
#SPJ11
