Answers
the measurement of QP=8 CM

Related Questions
Find the critical value tc for the confidence level c=0.99 and sample size n=15
Answers
The critical value of the confidence interval is Tc = 2.947
Given data ,
Let the confidence interval value be = 0.99
Now , the sample size is n = 15
And , For a confidence level of c = 0.99 and a sample size of n = 15 (which is relatively small), we will use a two-tailed t-distribution.
Using a t-distribution table or statistical software, the critical value tₓ for a confidence level of 0.99 and a sample size of 15 is approximately 2.947.
Hence , the critical value tₓ for a confidence level c = 0.99 and sample size n = 15 is approximately 2.947
To learn more about confidence interval click :
https://brainly.com/question/16807970
#SPJ1
Write an expression to represent the area of a right triangle with legs length as follow: 2x-2 and 4x+2
Answers
A=ab/2
(2x-2)(4x+2)/2
(8x^2+4x-8x-4)/2
(8x^2-4x-4)/2 take common term 2
2(4x^2-2x-2)/2
So A=4x^2-2x-2
Expression to represent the area of a right triangle with legs length as 2x-2 and 4x+2 is 4x² - 2x - 2.
What is expression?Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. The mathematical operators can be of addition, subtraction, multiplication, or division.
For example, x + y is an expression, where x and y are terms having an addition operator in between.
Given,
legs length of a right angle triangle = 2x-2 and 4x+2
Area of the right angle triangle = (length of leg a × length of leg b)/2
= (2x-2)(4x + 2)/2
= 2(x - 1)(4x + 2)/2
= (x - 1)(4x + 2)
Area of the right angle triangle = 4x² - 2x - 2
Hence, 4x² - 2x - 2 is the expression for area of right triangle.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ2
What is the slope of the line that goes through the points (1,4) and (13,10)?
Answers
Answer:
The slope is 1/2 :)
Step-by-step explanation:
Answer:
Step-by-step explanation:
(10 - 4)/(13 - 1) = 6/12 = 1/2 is the slope of the line
a roller coaster train with 6 passenger cars and the front decoration has a mass of 3,500kg. when the train has the front decoration and only 4 passenger cars, it has a mass of 2,400kg.
what is the mass of the decoration and of each passenger car?
Answers
The mass of the decoration and of each passenger car are 200 kg and 550 kg, respectively
How to determine the masses?The given parameters in the question are
6 passenger cars and the front decoration = 3,500kg4 passenger cars and the front decoration = 2,400kgThese can be represented as
(6, 3500) and (4, 2400)
The slope of the above points represent the mass of each passenger car
This is calculated as
Slope = Difference in mass/Difference in number of cars
So, we have
Slope = (3500 - 2400)/(6 - 4)
Evaluate
Slope = 550
When there are no passenger cars in the train, we have
(0, Mass of decoration)
Using the slope formula, we have
Slope = (Mass of decoration - 3500)/(0 - 6)
So, we have
Slope = (Mass of decoration - 3500)/(-6)
This gives
(Mass of decoration - 3500)/(-6) = 550
Cross multiply
Mass of decoration - 3500 = -3300
Add 3500 to both sides
Mass of decoration = 200
Hence, the mass of each car is 550 kg
Read more about slope at
https://brainly.com/question/29135291
#SPJ1
can someone help me with this question

Answers
Your hospital has just reset the safety stock level for sleeping pills to be 220 pills.
If your hospital consumes an average of 1,155 per day with a standard deviation of 81 pills, what is the chance that your hospital will run out of sleeping pills on any day? (Keep four decimal places in your answer, which should be a number not a percentage)
Answers
The chance that the hospital will run out of sleeping pills on any given day is 0.5000 (or 0.5000 with four decimal places).
To calculate the chance that the hospital will run out of sleeping pills on any given day, we can use the normal distribution and Z-score.
First, let's calculate the Z-score using the formula:
Z = (X - μ) / σ
Where:
X = consumption rate per day (1,155 pills)
μ = average consumption rate per day (1,155 pills)
σ = standard deviation (81 pills)
Z = (1,155 - 1,155) / 81
Z = 0
Now, we need to find the probability associated with this Z-score. However, since the demand for sleeping pills can be considered continuous and not discrete, we need to calculate the area under the curve from negative infinity up to the Z-score. This represents the probability of not running out of sleeping pills.
We discover that the region to the left of a Z-score of 0 is 0.5000 using a basic normal distribution table or statistical software.
To find the probability of running out of sleeping pills, we subtract this probability from 1:
Probability of running out of sleeping pills = 1 - 0.5000
Probability of running out of sleeping pills = 0.5000
Therefore, on any given day, the hospital has a 0.5000 (or 0.5000 with four decimal places) chance of running out of sleeping tablets.
Learn more about probability on:
https://brainly.com/question/23417919
Find the lowest common denominator (multiple). Type the equivalent fractions. Then, add or subtract. Simplify your answer. 1
2
1
3
Answers
Answer:what
Step-by-step explanation:what does this mean
help meeeeeeeeeeeeeeeeeee

Answers
Answer:
I believe its D and E
Step-by-step explanation:
Does that help
***HURRY TIMED TEST***
***WILL MARK BRAINLEST***
If f(x) = 8x + 7 and g(x) = square root x + 2, what is (fºg)(2)?
Answers
Answer:
\(8x + 7 =15 \\ gx + 2 =4 \\ \)
Mr. George is thirteenth from the top and twenty seventh from the bottom in the queue. How many persons are there in the queue
Answers
The number of persons in the line are 39.
According to the statement
We have given that the Mr. George is thirteenth from the top and twenty seventh from the bottom in the queue
And we have to find the number of persons in the queue.
So, For this purpose, we know that the
The given is that the position of the Mr. George is 27 from the last or bottom and
Mr. George is thirteenth from the top.
So, To find the total number of persons in the line we have to add the given numbers, here we have to find the number of persons in queue..
So he has skipped 12 numbers. 27th from bottom means it's 27+12=39 .
It means there are 39 persons in the line.
So, The number of persons in the line are 39.
Learn more about number of persons here
https://brainly.com/question/11408596
#SPJ4
A diagram of Joe's living room wall with a geometric design is shown. Joe painted the shaded triangle on the living room wall. What is the area in square feet of the shaded triangle that Joe painted?

Answers
Answer: the answer is 48
Step-by-step explanation:
Answer: 48
Step-by-step explanation: A triangles formula is base x height divided by 2, therefore we will do first 8 x 12 which equals 96, and divide by 2, giving us 48.
I need help filling in the blanks

Answers
Values of x for blanks 4 , 1 in inequality .
What in mathematics is an inequality number?
A relationship between two values in an algebraic statement that are not equal is shown by an inequality. One of the two variables on the two sides of the inequality can be represented by an inequality sign as greater than, greater than or equal to, less than, or equal to another value.
Despite the equals sign being substituted by an arrowhead, the formula 5x 4 > 2x + 3 resembles an equation. It serves as an illustration of inequity. This shows that the left half, 5x 4, is bigger than the right part, 2x + 3.
-3x/4 < 12/1
x < -16
Learn more about inequality
brainly.com/question/30231190
#SPJ1
Solve the problem. Round dollar amounts to the nearest cent. Use ordinary interest (360 days in a year) unless otherwise indicated. Chris Owens bought a new computer system. To pay for the system, he borrowed $3,290 from the credit union at 10(1/3)% interest for 110 days. Find the interest.
Answers
To find the interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days, we use the simple interest formula as follows:
Simple Interest = (P × R × T)/100Where:P = Principal or amount borrowedR = Rate of interest per annumT = Time in years or fraction of a year110 days ÷ 360 days = 0.3056 (time as a fraction of a year)The rate of interest, 10(1/3)% is equal to 10 + (1/3) percent = 10.33% per annum in decimal form = 0.1033Substituting the values we have into the formula,Simple Interest = (P × R × T)/100= (3,290 × 0.1033 × 0.3056)/100= $100.68 (rounded to the nearest cent)
Therefore, the interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days is $100.68.
A credit union loan is a type of personal loan that can be used for a variety of purposes. One of the most common reasons people take out credit union loans is to purchase big-ticket items like a new computer system. When you take out a loan, you must pay back the amount borrowed plus the interest charged by the lender. The interest rate is usually expressed as a percentage of the amount borrowed and is charged for a specific period of time known as the loan term. Simple interest is a method of calculating interest that is charged only on the principal amount borrowed.
It does not take into account the interest that has already been paid. Simple interest is calculated by multiplying the principal amount borrowed by the interest rate and the length of the loan term. The answer is more than 100 words.The interest of Chris Owens’ credit union loan of $3,290 at 10(1/3)% interest for 110 days is $100.68. Therefore, he would pay $3,290 + $100.68 = $3,390.68 in total to the credit union over the loan term. It is important to note that when rounding dollar amounts to the nearest cent, amounts that end in .50 or higher are rounded up to the next highest cent, while amounts that end in .49 or lower are rounded down to the next lowest cent. In this case, $100.6847 would be rounded up to $100.68. In conclusion, the interest charged on a loan can significantly increase the total amount that must be repaid, making it important for borrowers to understand how interest is calculated and the terms of their loan.
To know more about Chris Owens’ visit
https://brainly.com/question/11904608
#SPJ11
2p2 - 5p + 3
pliss anwered this for me
Answers
Answer:
2p²-5p+3 is the final answer as they aren't any like terms to collect in order to simply the solution further.
Step-by-step explanation:
Wishing you a splendiferous day,
stay salty...
3 1/5 as a equivalent decimal
Answers
Answer:
3.20 there is your answer
Frame zero, F0. is the fixed global frame. For each of
the cases below find T 1: 0
(a) F1 is rotated by an angle θ about zo.
(b) F1 is rotated by θ about xo.
(c) F1 is rotated by θ about yo.
Answers
(a) `T1:0 = [cos150 sin150 0 0; -sin150 cos150 0 0; 0 0 1 0; 0 0 0 1]`
(b) `T1:0 = [1 0 0 0; 0 cos150 sin150 0; 0 -sin150 cos150 0; 0 0 0 1]`
(c) `T1:0 = [cos150 0 -sin150 0; 0 1 0 0; sin150 0 cos150 0; 0 0 0 1]`
Given that Frame zero, F0 is the fixed global frame.
For each of the cases below find T1
Case (a)
F1 is rotated by an angle θ about zo.
Let O be the origin of the fixed frame F0, A be the origin of the frame F1 and α be the angle between the x-axis of the frame F0 and the projection of the x-axis of the frame F1 on the xy plane of the frame F0.
Let l, m, n be the direction cosines of the vector from O to A, expressed in F0.
The content-loaded frame zero F0 is the fixed global frame, which means that the vectors i, j, k representing the x, y, and z-axis of F0 are fixed and cannot be transformed.
Therefore, the transformation matrix T1:0
in this case is:
`T1:0 = [l1 m1 n1 0; l2 m2 n2 0; l3 m3 n3 0; 0 0 0 1]`
Case (b)
F1 is rotated by θ about xo.
Let β be the angle between the y-axis of F0 and the projection of the y-axis of F1 on the yz plane of F0.
Let γ be the angle between the z-axis of F0 and the projection of the z-axis of F1 on the zx plane of F0.
The transformation matrix T1:0
in this case is given by:
`T1:0 = [1 0 0 0; 0 cosθ sinθ 0; 0 -sinθ cosθ 0; 0 0 0 1]`
Case (c)
F1 is rotated by θ about yo.
Let β be the angle between the y-axis of F0 and the projection of the y-axis of F1 on the yz plane of F0.
Let γ be the angle between the z-axis of F0 and the projection of the z-axis of F1 on the zx plane of F0.
The transformation matrix T1:0
in this case is given by:
`T1:0 = [cosθ 0 -sinθ 0; 0 1 0 0; sinθ 0 cosθ 0; 0 0 0 1]`
Thus, the transformation matrix T1:0
for the three cases (a), (b), and (c) are given as follows:
(a) `T1:0 = [cosθ sinθ 0 0; -sinθ cosθ 0 0; 0 0 1 0; 0 0 0 1]`
(b) `T1:0 = [1 0 0 0; 0 cosθ sinθ 0; 0 -sinθ cosθ 0; 0 0 0 1]`
(c) `T1:0 = [cosθ 0 -sinθ 0; 0 1 0 0; sinθ 0 cosθ 0; 0 0 0 1]`
Given θ = 150,
T1:0 for the three cases are:
(a) `T1:0 = [cos150 sin150 0 0; -sin150 cos150 0 0; 0 0 1 0; 0 0 0 1]`
(b) `T1:0 = [1 0 0 0; 0 cos150 sin150 0; 0 -sin150 cos150 0; 0 0 0 1]`
(c) `T1:0 = [cos150 0 -sin150 0; 0 1 0 0; sin150 0 cos150 0; 0 0 0 1]`
Learn more about transformation matrix from this link:
https://brainly.com/question/31505232
#SPJ11
the probability of serena serving an ace n tennis is 0.15, and the probability that she double faults is 0.25. what is the probability that serena does not serve an ace or a double fault?
Answers
The probability that Serena does not serve an ace or a double fault is 0.63..
Addition rule of probability applies to the calculation of probability for one or another event happen. These events are either mutually exclusive or not .
We have following information,
The probability of Serena serving an ace in tennis (p) = 0.15
Probability that she double faults(q) = 0.25
The probability of Serena not serving an ace in tennis = 1 -p = 1 - 0.15 = 0.85
let A and B be two events Serena not serving an ace and she double faults respectively.
Events A and B are not mutually exclusive events .
i.e, P(A ∩ B ) =/ 0
when Serna not serving an ace implies that either it is double faults or not and both have equally likely chance.
So, the probability of intersection of event A and B = 0.85/2 = 0.47
Adding Rule for probabilities is
P(A or B ) = P(A) + P(B) - P(A ∩ B)
The probability that Serena does not serve an ace or a double fault = 0.85 + 0.25 - 0.47
= 1.10 - 0.47 = 0.63...
Hence, the probability that Serena does not serve an ace or double fault is 0.63..
To learn more about Probability, refer:
https://brainly.com/question/13604758
#SPJ4
Can someone please tell what is the right answer and why it’s righ btw it’s not B because I did it and got it wrong
Answers
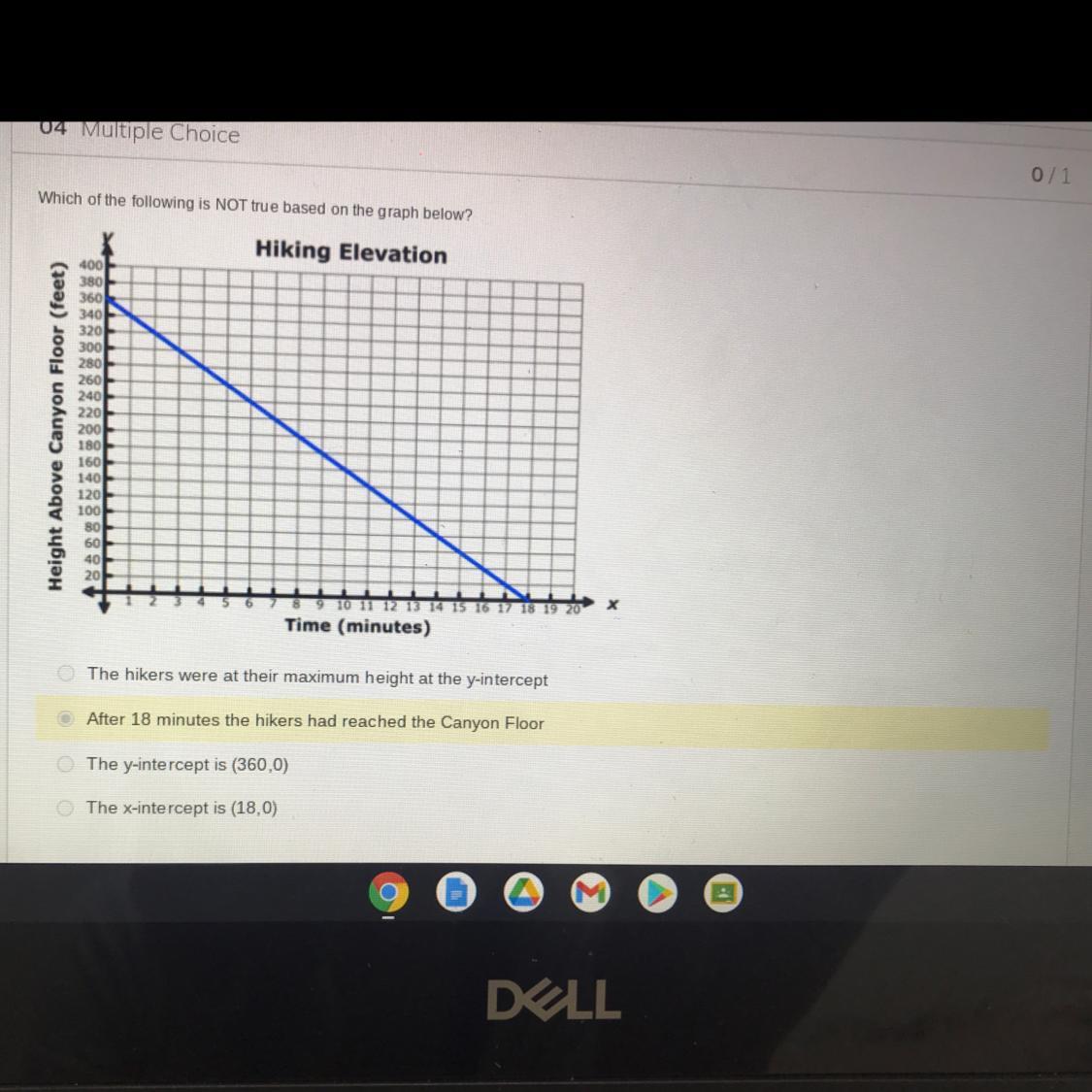
It is (0,360) lol
I am attaching a picture of the question as you can see my teacher has already answered it but she wants me to show how she got the answer

Answers
Surface area of a square pyramid:
\(\begin{gathered} SA=B+\frac{1}{2}p\cdot s \\ \\ B=\text{area of the base} \\ p=\text{perimeter of the base} \\ s=\text{slant height} \end{gathered}\)To find the surface area of the given pyramid as you don't have the length of the slant height, use the height of the pyramid and the radius of the base to form a right triangle and find the slant height:
Pythagorean theorem for the right triangle above:
\(\begin{gathered} s^2=h^2+(\frac{1}{2}b)^2 \\ \\ s=\sqrt[]{h^2+(\frac{1}{2}b)^2} \\ \\ s=\sqrt[]{(12in)^2+(\frac{1}{2}\cdot18in)^2} \\ \\ s=\sqrt[]{(12in)^2+(9in)^2} \\ \\ s=\sqrt[]{144in^2+81in^2} \\ \\ s=\sqrt[]{225in^2} \\ \\ s=15in \end{gathered}\)Perimeter of the base is:
\(\begin{gathered} p=4b \\ p=4\cdot18in \\ p=72in \end{gathered}\)Area of the square base:
\(\begin{gathered} B=b^2 \\ B=(18in)^2 \\ B=324in^2 \end{gathered}\)Then, the surface area of the given pyramid is
\(\begin{gathered} SA=324in^2+\frac{1}{2}\cdot72in\cdot15in \\ \\ SA=324in^2+540in^2 \\ SA=864in^2 \end{gathered}\)

a new trendy restaurant is growing exponentially. after being open for 11 months the restaurant was serving an average of 310 customers a day. by month 15, the restaurant was serving about 456 customers a day. write an exponential function n(t) that models average number of customers, n, after t months of being open. if necessary, round any values to four decimal places (do not round on intermediate steps). write your answer in the form a(b)t
Answers
the exponential function is n(t) =n° (1+r)∧t, where t is the power refers the time in months after opening and n denotes average customer.
what means growing exponentially?when the rate of increases is occurred very rapidly. In this question, the trendy restaurant has earned reputation.
How will be the exponential function?Given, average number of customers after 11 months of opening = n(11) =310
average number of customers after 15 months of opening= n(15) =456
during this 4 month increases of customer =456 -310 =146
increasing rate of customer per month = 146/4 = 36.5
now increasing rate in percentages = 36.5 %
exponential growth rate, r= 0.365
let, n° is the initial number of customer while opening at t=0 month
now, the exponential function n(t) that model's average number of customers, n after t months of being open will be
n(t) = n° ( 1+r)∧t
we are given that after 11 months of opening average customer n(11) = 310
now, 310 = n° (1+ 0.365)∧11
n° = 10
hence, the exponential function = n(t) = 10(1+r)∧t
to learn more about exponential growth function visit:
https://brainly.com/question/2456547
#SPJ4
a group of 90 students is to be split at random into 3 classes of equal size. all partitions are equally likely. joe and jane are members of the 90-student group. find the probability that joe and jane end up in the same class.
Answers
The probability that joe and jane end up in the same class is 0.3258 .
In the question ,
it is given that
90 students is to be split into 3 equal size classes , so ,
the three classes will have 30 students each .
let these classes be Class A , Class B and Class C .
Let Joe and Jane be in Class A .
the total number of ways of selecting 30 students for class A from 90 students is C(90,30) .
Since , we have fixed Joe and Jane in Class A , the remaining 28 spots of class A can be filled by remaining 88 students in C(88,28) ways ,
So , the probability that Joe and Jane end up in the same class is
= C(88,28)/C(90,30) .
Since there are three classes ,
the required probability is 3*C(88,28)/C(90,30) .
= 3×\(\frac{88!}{28!*60!}\)×\(\frac{60!*30!}{90!}\)
= 29/89
= 0.3258
Therefore , the probability that joe and jane end up in the same class is 0.3258 .
Learn more about Probability here
https://brainly.com/question/8885214
#SPJ1
Can you provide the solution for this exercise?
Let u(w) = −(b − w)c. What restrictions on w, b, and c are required to ensure that u(w) is strictly increasing and strictly concave? Show that under those restrictions, u(w) displays increasing absolute risk aversion.
Answers
under the restrictions that c is negative to ensure strict concavity, the utility function u(w) = -(b - w)c displays increasing absolute risk aversion.
To ensure that u(w) is strictly increasing, we need the derivative of u(w) with respect to w to be positive for all values of w. Taking the derivative, we have du(w)/dw = -c. For u(w) to be strictly increasing, -c must be positive, which implies c must be negative.
To ensure that u(w) is strictly concave, we need the second derivative of u(w) with respect to w to be negative for all values of w. Taking the second derivative, we have d²u(w)/dw² = 0. Since the second derivative is constant and negative, u(w) is strictly concave.
Now, let's examine the concept of increasing absolute risk aversion. If a utility function u(w) exhibits increasing absolute risk aversion, it means that as wealth (w) increases, the individual becomes more risk-averse.
In the given utility function u(w) = -(b - w)c, when c is negative (as required for strict concavity), the absolute risk aversion increases as wealth (w) increases. This is because the negative sign implies that the utility function is concave, indicating that the individual becomes more risk-averse as wealth increases.
Learn more about utility function here:
https://brainly.com/question/31498128
#SPJ11
im struggling with this :D i need help!

Answers
Answer:
not a real number
Step-by-step explanation:
any negative number under a square root sign, except for 0, isn't real
On evaluating the given roots,
(a) \($-(\sqrt[3]{8}) = -2$\)
(b) \($\sqrt[4]{-81}$\) is not a real number
(a) \($-(\sqrt[3]{8})$\):
The cube root of 8 is the number that, when raised to the power of 3, equals 8. In this case, the cube root of 8 is 2, because \(2^3 = 8\).
Since we have a negative sign in front of the cube root, the result will be the negative value of the cube root of 8.
Therefore, \($-(\sqrt[3]{8}) = -2$\).
(b) \($\sqrt[4]{-81}$\):
The fourth root of a number is the number that, when raised to the power of 4, equals the given number.
In this case, we are looking for the fourth root of -81.
However, the fourth root of a negative number is not a real number. This is because raising a positive number to an even power (in this case, 4) will always result in a positive value, and there is no real number that, when raised to the power of 4, gives a negative result.
Therefore, the fourth root of -81 is not a real number.
To know more about roots, refer here:
https://brainly.com/question/12105008
#SPJ2
*XTRA PTS* can someone please explain how to find the domain and the range of a coordinate/set of relations
Answers
Answer:
Domain: X coordinates
Range: Y coordinates
Step-by-step explanation:
The domain is the set of all first elements of ordered pairs (x-coordinates). The range is the set of all second elements of ordered pairs (y-coordinates). Only the elements "used" by the relation or function constitute the range. Domain: all x-values that are to be used (independent values).The range is the set of all second elements of ordered pairs (y-coordinates). Only the elements "used" by the relation or function constitute the range. Domain: all x-values that are to be used (independent values). Range: all y-values that are used (dependent values).
a 5 pound bag of apples costs $4.50, and an 8 pound bag of the same type of apples costs $7.52. greg found the unit price between the cost and weight for each bag of apples. what is the difference between the unit prices?
Answers
Answer:
Step-by-step explanation: $3.02
3 pounds difference
for numbers 19 and 20 you have to solve for the missing angle.

Answers
Answer:19. 17 degrees
20. 49 degrees
Step-by-step explanation:
Because of the postulate 50+?=67
So ?=17
And 20.
94+?=143
So
?=49
(Edit)I though you only meant 19 and 20
21. X=8
22. X=12
23.x=8
24.x=7
Marisol is making a rectangular wooden frame. She wants the length of the frame to be no more than 12 inches. She has less than 30 inches of wood to use. Which system of inequalities represents the possible length, l, and the possible width, w, that her frame could have?
l ≤ 12
2l + 2w < 30
l > 12
2l + 2w < 30
l ≤ 12
l + w < 30
l > 12
l + w < 30
Answers
The system of inequalities represents the possible length, l, and the possible width, w, that her frame could have is l ≤ 12 and 2l + 2w < 30
How to determine the system of inequalities represents the possible length, l, and the possible width, w, that her frame could have?The given parameters are
Length = Not more than 12 inches
Perimeter = Less than 30 inches
"Not more than" means less than or equal to
So, we have
l ≤ 12
The perimeter of a rectangle is
P = 2l + 2w
So, we have
2l + 2w = Less than 30 inches
"Less than" is represented with <
So, we have
2l + 2w < 30
Hence, the system of inequalities represents the possible length, l, and the possible width, w, that her frame could have is l ≤ 12 and 2l + 2w < 30
Read more about system of inequalities at
https://brainly.com/question/9290436
#SPJ1
Answer:
a. I ≤ 12
2l + 2w < 30
Step-by-step explanation:
i got it right on edge.

a farmer is tilling a rectangular field that is 72 yards long and 65 yards wide. what is the distance between opposite corners of the farmer's field?
Answers
The distance between opposite corners of the farmer's rectangular field is 97 yards.
The distance between opposite corners of a rectangular field can be calculated using the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
In this case, the opposite corners of the rectangular field form the two shorter sides of a right triangle, and the distance between them is the hypotenuse.
To apply the Pythagorean theorem, we can label the length of the field (72 yards) as one side, and the width of the field (65 yards) as the other side. The distance between the opposite corners (the hypotenuse) can then be calculated as follows:
Distance between opposite corners = √(length² + width²)
= √(72² + 65²)
= √(5184 + 4225)
= √9409
= 97
To learn more about rectangle click on,
https://brainly.com/question/16530331
#SPJ4
How many solutions do the following linear equations have?

Answers
The following linear equations have no solution.
What is linear equation?
Since each term in a linear equation has an exponent of 1, an algebraic equation may always be graphed as a straight line. It is known as a "linear equation" because of this.
A linear equation is one that has a maximum degree of 1.
Given,
y=x/2+4 and y=x/2+8
The basic form is y=mx+c.
In this equation m is the slope.
Here both lines have the same slope here, m=1/2 but distinct y-intercepts, it is simple to determine whether the given equation has no solution.
When a problem has no solution, it indicates that the two lines are parallel and never cross.
To learn more about linear equation from the given link
https://brainly.com/question/2030026
#SPJ1
if the arithmetic mean of 5 and c is 11,what is the value of c?
Answers
Answer:
c = 17
Step-by-step explanation:
(c + 5) : 2 = 11
c + 5 = 22
c = 17
If the arithmetic mean of 5 and c is 11, the value of c is 17.
What is the interpretation of average?Arithmetic mean is the best central measure available for representing the values of a data set. It is also called average of the values of the considered data set.
It serves as predicted value(in case no other information of the data is available) of that data set.
Average provides ill information in case of skewed data.
If the arithmetic mean of 5 and c is 11, then the value of c.
(c + 5) : 2 = 11
c + 5 = 22
c = 17
Hence, the value of c is 17.
Learn more about arithmetic here:
brainly.com/question/14753192
#SPJ2
