Find the mean for this list of numbers 75 41 49 78 31 26 79 1 89 95 94 3 4 33 88 Mean = = Find the mode for this list of numbers 51 15 25 46 76 13 99 34 87 15 54 5 94 7 38 Mode =
Answers
The mean for this list of numbers is 52.4 and the mode of the given list is 15.
Apart from the mode and median, the mean is one of the measures of central tendency in statistics. The mean is just the average of the values in a given set. It denotes an equal distribution of values for a particular data set.
The three most popular measures of central tendency are the mean, median, and mode. To determine the mean, add the total values in a datasheet and divide the result by the total number of values. Mode is the number in the list that is repeated the most amount of times.
Mean = (sum of all observations divided by total number of observations)
Sum of total observations = 75 + 41 + 49 + 78 + 31 + 26 + 79 + 1 + 89 + 95 + 94 + 3 + 4 + 33 + 88 = 786
Total number of observations = 15
Mean = 786 / 15
= 52.4
For mode, we consider the frequency of the number. In this list, all numbers have frequency of 1 except 15 which has frequency of 2, hence mode is 2.
To know more about mean and mode:
https://brainly.com/question/6813742
#SPJ4
Related Questions
cho tam giác ABC cân tại A trung tuyến AM.Biết BC=6cm,AM=4cm .Tính độ dài các cạnh AB và AC
Answers
Vì tam giác ABC cân tại A (gt) mà AM là đg trung tuyến nên AM đồng thời là đg cao của t/giác đó:
AM là trung tuyến của t/giác ABC nên M là trung điểm BC:
=> BM =BC/2 =6:2=3(cm)
Xét tam giác AMB vuông tại M
AB^2 =AM^2+BM^2 ( theo định lý Py-ta -go)
58.21 + ( -139.58 ) Do I do KCO?
Answers
Answer:
2136
Step-by-step explanation:
Is anyone in the 9th grade learning bout Multiplying Polynomials and and learning boutFOIL (First,Outside,Inside,Last)
Answers
Answer:
lol I'm a senior, you'll have to do the foil method for the rest of high school and college
The midpoint of AB is (-2,0). If the coordinates of A are (-6,8), what are the
coordinates of B
Answers
Answer:
coordinate of B(2,-8)
Answer:
(4,-8)
Step-by-step explanation:
The stem-and-leaf plot displays the distances that a heavy ball was thrown in feet.
2 0, 2, 5
3 1, 3, 4
4 1, 1, 5
5 0, 6
6 7
Key: 3|1 means 3.1
What is the mean, and what does it tell you in terms of the problem?
Answers
The heavy ball was hurled an average distance of 3.85 feet, according to the mean.
How can the mean of a data set with a stem-and-leaf plot be calculated?List out all the data values that are represented on the stem-and-leaf plot, add up all the values, then divide by the total number of values that were represented on the stem-and-leaf plot to obtain the mean of the data set.
Using the key and the stem-and-leaf plot above, the following data points are depicted:
2.0, 2.1, 2.4, 3.1, 3.2, 3.6, 4.1, 4.3, 4.7, 5.1, 5.1, 6.5
Mean = [2.0 + 2.1 + 2.4 + 3.1 + 3.2 + 3.6 + 4.1 + 4.3 + 4.7 + 5.1 + 5.1 + 6.5]/12
Mean = 46.2/12
Mean = 3.85 feet
Therefore, the heavy ball was hurled at an average distance of 3.85 feet, according to the mean.
Know more about the mean of data on:
brainly.com/question/11015069
#SPJ1
Correct question:
The stem-and-leaf plot displays the distances from that a heavy ball was thrown in feet.
2 0, 1, 4
3 1, 2, 6
4 1, 3, 7
5 1, 1
6 5
Key: 3|2 means 3.
What is the mean, and what does it tell you in terms of the problem?
Use a proportion to convert the measurement.
10 yards =_______meters
Answers
9.144 meters are in 10 yards.
Answer:
9.144
Step-by-step explanation:
Convert Yards to Meters calculator.
HELP ASAP PLEASEEEEE
100 POINTS
An equation is shown: x2 + 4x + 4 = 0
What are the x intercepts? Show your work using a method of your choice.
What is an alternate method you could use to find the x intercepts (other than the method you used)?
What is the vertex? Is it a minimum or maximum? How do you know by looking at the equation?
What steps would you take to graph using the information you have already calculated? How would you use symmetry to help you graph?
Answers
The y-intercept is (0, 4).
An alternate method to find the x-intercepts is to factor the quadratic equation.
The vertex is (-2, 0).
The graph of the equation is illustrated below.
One of the most common types of equations is a quadratic equation, which is an equation of the form ax² + bx + c = 0. In this case, we have the equation x² + 4x + 4 = 0, and we need to find the x-intercepts.
To find the x-intercepts, we can use the quadratic formula, which is given by:
x = (-b ± √(b² - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation. In this case, a = 1, b = 4, and c = 4, so we can substitute these values into the formula:
x = (-4 ± √(4² - 4(1)(4))) / 2(1) x = (-4 ± √(0)) / 2 x = -2
Therefore, the x-intercept is -2. We can check this by plugging in x = -2 into the equation and verifying that it equals zero:
(-2)² + 4(-2) + 4 = 0
In this case, we can see that the equation can be factored as:
(x + 2)² = 0
Taking the square root of both sides, we get:
x + 2 = 0
x = -2
This gives us the same x-intercept as before.
To find the vertex of the parabola represented by the equation, we can use the formula:
x = -b / 2a
and then substitute this value of x into the equation to find the y-coordinate of the vertex. In this case, we have:
x = -4 / 2(1) x = -2
Substituting x = -2 into the equation, we get:
(-2)² + 4(-2) + 4 = 0
Since the coefficient of x² is positive (i.e., a = 1 > 0), the parabola opens upwards and the vertex is a minimum.
To graph the parabola, we can plot the vertex at (-2, 0) and use the x-intercept we found earlier at (-2, 0). Since the equation is symmetric about the vertical line through the vertex, we know that there is another point on the graph that is the same distance from the vertex but on the other side of the line. Therefore, we can plot the point (-3, 0) as well. We can also find the y-intercept by setting x = 0 in the equation:
0² + 4(0) + 4 = 4
Using this information, we can sketch the parabola by connecting the points (-3, 0), (-2, 0), and (0, 4), and noting that the parabola is symmetric about the line x = -2.
To know more about equation here
https://brainly.com/question/10413253
#SPJ1

What are the tax consequences to Euclid from the following independent events? In your computations, do not round intermediate division. If required, round the per share answer to two decimal places. Round all other answers to the nearest dollar. a. Euclid bought 500 shares of common stock five years ago for $50,000. This year, Euclid receives 20 shares of common stock as a nontaxable stock dividend. As a result of the stock dividend, Euclid's per share basis is $ X. b. Assume instead that Euclid received a nontaxable preferred stock dividend of 20 shares. The preferred stock has a fair market value of $5,000, and the common stock, on which the preferred is distributed, has a fair market value of $75,000. After the receipt of the stock dividend, the basis of the preferred stock is $ X, and the basis of the common stock is Φ
Answers
Euclid receives 20 shares of common stock as a nontaxable stock dividend.The basis of the common stock remains the same as in scenario a, which is $96.15 per share.
To calculate the per share basis, we divide the original purchase cost by the total number of shares (including the dividend shares). In scenario b, Euclid receives a nontaxable preferred stock dividend of 20 shares. The preferred stock has a fair market value of $5,000, and the common stock, on which the preferred is distributed, has a fair market value of $75,000.
The tax consequences involve determining the new basis of the preferred stock and the common stock after the dividend. a. To find the per share basis of Euclid's common stock after receiving the stock dividend, we divide the original purchase cost by the total number of shares. The original purchase cost was $50,000 for 500 shares, which means the per share basis was $50,000/500 = $100. After receiving 20 additional shares as a dividend, the total number of shares becomes 500 + 20 = 520.
Therefore, the new per share basis is $50,000/520 = $96.15. b. In this scenario, Euclid receives a preferred stock dividend of 20 shares. The preferred stock has a fair market value of $5,000, and the common stock has a fair market value of $75,000. To determine the new basis of the preferred stock, we consider its fair market value.
Since the preferred stock dividend is nontaxable, its basis is equal to the fair market value, which is $5,000.
Learn more about shares here: brainly.com/question/32277750
#SPJ11
Which of the following is equivalent to (27/y^6)^-1/3
Pls help

Answers
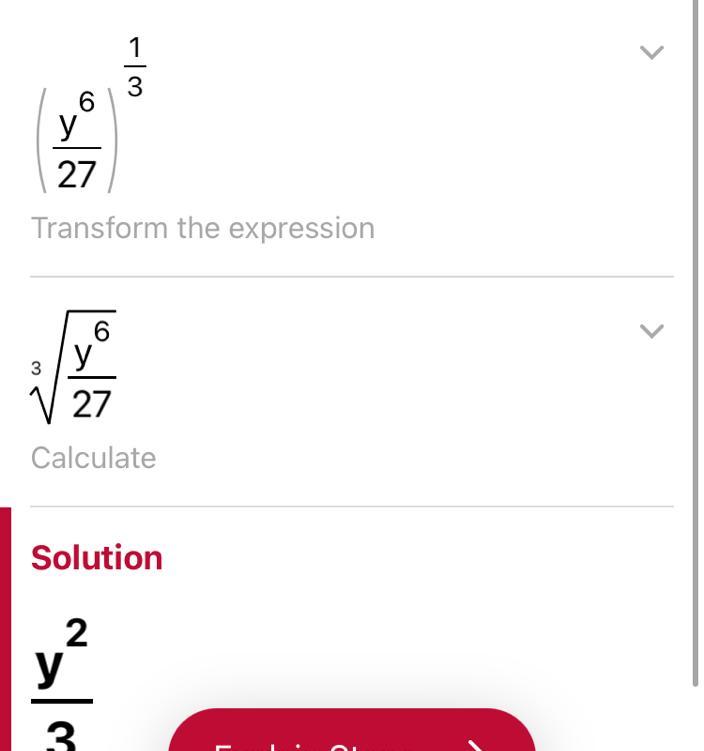
Write an equation to determine the unknown side. Then solve the equation. Simplify your answer. Round to the nearest tenth, if necessary.
Show your work.
A right triangle is shown. The hypotenuse is labeled 12, one leg is labeled 4, and the other leg is labeled x.
Answers

The y-intercept of a line has the same value as its gradient. If this line cuts the curve y = \(x^{3}\) – 2\(x^{2}\) – 3x – 8 at x = 3, find the equation of the line.
Select one:
a. 2x − y + 2 = 0
b. 2x + y + 2 = 0
c. 2x + y − 2 = 0
d. None of these
Answers
Answer:
B. 2x+y+2+=0
Step-by-step explanation:
Given: x=3
First: you substitute for x in y=x^3-2x^2-3x-8
y=(3)^3-2(3)^2-3(3)-8
y=-8
Now all you have to do is plug y in each of the answers until you get 3 for x.
A. 2x-(-8)+2=0
2x+10=0
2x=-10
x=-5
B. 2x+(-8)+2=0
2x-6=0
2x=6
x=3
C. 2x+(-8)-2=0
2x-10=0
2x=10
x=5
Find the sum.
eleven and eight hundredths added to two and thirty-five hundredths
The sum is ?
Answers
Answer:
16.43
Step-by-step explanation:
Answer:
Step-by-step explanation:
here is the answer i hope this helps

Solve the equation.
-3x + 1 + 10x = x + 4
O x=1/2
O x=12 /2
O x = 12
O x = 18
Answers
Answer:
a) x=1/2
Step-by-step explanation:
Plug In
-3 (1/2) + 1 + 10 (1/2) = 1/2 + 4
:)
What is the percent if 200 is the total and 150 is the part?
Answers
Answer:
75%
Step-by-step explanation:
75% of 200 is 150
Answer:
75% since \(50 + 50 + 50 = 150\) which is \(3\) quarters of \(200\)
Please mark brainliest.
Without any programs, form a polynomial function of degree 2 with zero points x = 1 and x = 3 and whose graph passes through the point (5, 4).
BALIIIISS AND BALIIS
Answers
Answer:
\(y= \frac12 x^2 -2x +\frac32\)
Step-by-step explanation:
From the two zeroes, you can tell that the polynomial factors as \(y= A(x-1)(x-3)\). You have still one degree of freedom (determining how wide the parabola is. You can determine it with the other condition:
\(4 = A(5-1)(5-3) \rightarrow 4= A(4)(2) \rightarrow A= \frac12\)
Your function is \(y= \frac12 (x-1)(x-3) = \frac12 x^2 -2x +\frac32\)
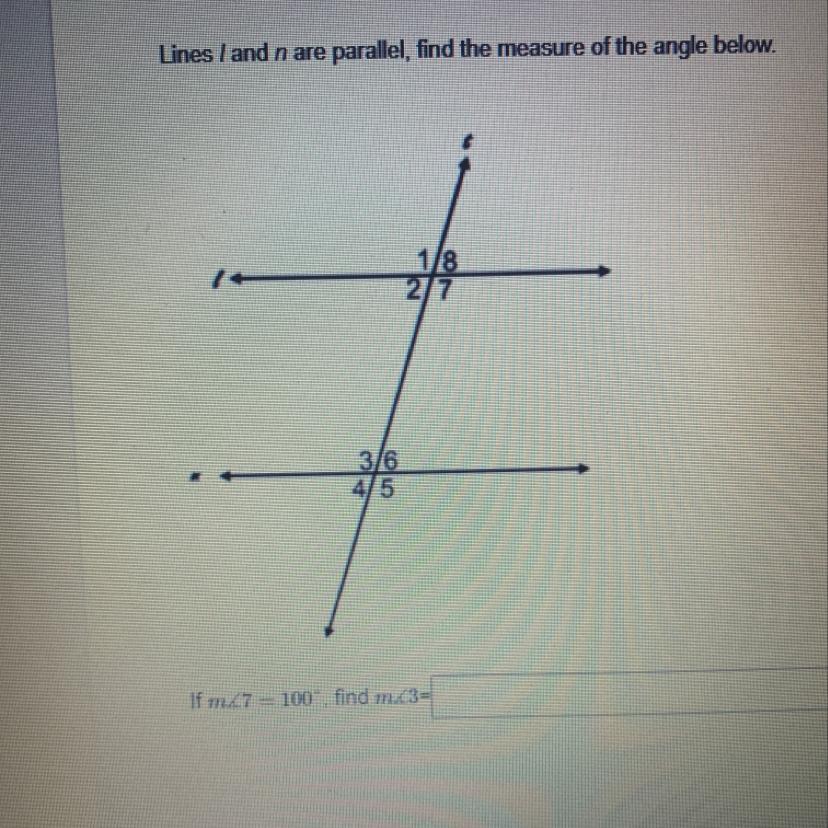
If m7 is 100 find m3
Answers
Answer:
m3 is 100 degrees
Step-by-step explanation:
In this case, angle 7 is congruent to angle 5 because both their angles are located on the same place in different lines. Another rule you need to know is that angles across from each other are equal. So, if angle 5 is 100 degrees, then angle 3 is also 100 degrees because they are across from each other.
A town has a population of 5000 and grows at 3. 5% every year. What will be the population after 15 years, to the nearest whole number?.
Answers
Answer:
26,2500
Step-by-step explanation:
please assist with helping in the image below!!

Answers
Write the expression in standard form a+bi: (8-i)/(2+i)
Answers
Answer:
The expression (8-i)/(2+i) in standard form is, 3 - 2i
Step-by-step explanation:
The expression is,
(8-i)/(2+i)
writing in standard form,
\((8-i)/(2+i)\\\)
Multiplying and dividing by 2+i,
\(((8-i)/(2+i))(2-i)/(2-i)\\(8-i)(2-i)/((2+i)(2-i))\\(16-8i-2i-1)/(4-2i+2i+1)\\(15-10i)/5\\5(3-2i)/5\\=3-2i\)
Hence we get, in standard form, 3 - 2i
The expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
To write the expression (8-i)/(2+i) in standard form a+bi, we need to eliminate the imaginary denominator. We can do this by multiplying the numerator and denominator by the conjugate of the denominator.
The conjugate of 2+i is 2-i. So, we multiply the numerator and denominator by 2-i:
(8-i)/(2+i) * (2-i)/(2-i)
Using the distributive property, we can expand the numerator and denominator:
(8(2) + 8(-i) - i(2) - i(-i)) / (2(2) + 2(i) + i(2) + i(i))
Simplifying further:
(16 - 8i - 2i + i^2) / (4 + 2i + 2i + i^2)
Since i^2 is equal to -1, we can substitute -1 for i^2:
(16 - 8i - 2i + (-1)) / (4 + 2i + 2i + (-1))
Combining like terms:
(15 - 10i) / (3 + 4i)
Therefore, the expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
Learn more:About complex numbers here:
https://brainly.com/question/20566728
#SPJ11
The following data show the frequency of rainy days in a year less than 0.01 inch 165 days 0.01 -1 inch 90 days 1.01 - 5 inches 60 days 5.01 -10 inches 40 days more than 10 inches 10 days Find the mode.
Answers
The mode of a dataset is the value that appears most frequently. In this case, we need to find the interval of rainfall that occurs most frequently.
From the given data, we can see that the interval "less than 0.01 inch" has the highest frequency with 165 days. Therefore, the mode of this dataset is "less than 0.01 inch"
Effective communication is crucial in all aspects of life, including personal relationships, business, education, and social interactions. Good communication skills allow individuals to express their thoughts and feelings clearly, listen actively, and respond appropriately. In personal relationships, effective communication fosters mutual understanding, trust, and respect.
In the business world, it is essential for building strong relationships with clients, customers, and colleagues, and for achieving goals and objectives. Good communication also plays a vital role in education, where it facilitates the transfer of knowledge and information from teachers to students.
Moreover, effective communication skills enable individuals to engage in social interactions and build meaningful connections with others. Therefore, it is essential to develop good communication skills to succeed in all aspects of life.
Learn more about dataset here:
https://brainly.com/question/26468794
#SPJ11
A line passes through the points (-4, 7) and (5, -8). What is the slope of the line?
Answers
Answer:
slope={-8-7}/{5--4)=-15/9=-5/3
we use - × -=+
Suppose that 14 bluebirds and 11 robins are trying out for a choir that will have 7 members. How many ways can this choir be formed if it must have more bluebirds than robins?.
Answers
The number of ways this choir be formed if it must have more bluebirds than robins is 3111740
Total number of bluebirds = 14 bluebirds
Total number of robins = 11 robins
The members of the choir = 7 members
The possible combinations are
7 bluebirds = \(14C_7\) = 3432
6 bluebirds and 1 robin = \(14C_6\) × \(11C_1\) = 33033
5 bluebirds and 2 robins = \(14C_5\) × \(11C_2\) = 110110
4 bluebirds and 3 robins = \(14C_4\) × \(11C_3\) = 165165
Total combinations = 3432 + 33033 + 110110 + 165165
= 311740
Hence, the number of way this choir be formed if it must have more bluebirds than robins is 3111740
Learn more about combinations here
brainly.com/question/28720645
#SPJ4
Find the directional derivative of the function at the given point in the direction of the vector v.
f(x, y) = 7 e^(x) sin y, (0, π/3), v = <-5,12>
Duf(0, π/3) = ??
Answers
The directional derivative of the function at the given point in the direction of the vector v are as follows :
\(\[D_{\mathbf{u}} f(\mathbf{a}) = \nabla f(\mathbf{a}) \cdot \mathbf{u}\]\)
Where:
- \(\(D_{\mathbf{u}} f(\mathbf{a})\) represents the directional derivative of the function \(f\) at the point \(\mathbf{a}\) in the direction of the vector \(\mathbf{u}\).\)
- \(\(\nabla f(\mathbf{a})\) represents the gradient of \(f\) at the point \(\mathbf{a}\).\)
- \(\(\cdot\) represents the dot product between the gradient and the vector \(\mathbf{u}\).\)
Now, let's substitute the values into the formula:
Given function: \(\(f(x, y) = 7e^x \sin y\)\)
Point: \(\((0, \frac{\pi}{3})\)\)
Vector: \(\(\mathbf{v} = \begin{bmatrix} -5 \\ 12 \end{bmatrix}\)\)
Gradient of \(\(f\)\) at the point \(\((0, \frac{\pi}{3})\):\)
\(\(\nabla f(0, \frac{\pi}{3}) = \begin{bmatrix} \frac{\partial f}{\partial x} (0, \frac{\pi}{3}) \\ \frac{\partial f}{\partial y} (0, \frac{\pi}{3}) \end{bmatrix}\)\)
To find the partial derivatives, we differentiate \(\(f\)\) with respect to \(\(x\)\) and \(\(y\)\) separately:
\(\(\frac{\partial f}{\partial x} = 7e^x \sin y\)\)
\(\(\frac{\partial f}{\partial y} = 7e^x \cos y\)\)
Substituting the values \(\((0, \frac{\pi}{3})\)\) into the partial derivatives:
\(\(\frac{\partial f}{\partial x} (0, \frac{\pi}{3}) = 7e^0 \sin \frac{\pi}{3} = \frac{7\sqrt{3}}{2}\)\)
\(\(\frac{\partial f}{\partial y} (0, \frac{\pi}{3}) = 7e^0 \cos \frac{\pi}{3} = \frac{7}{2}\)\)
Now, calculating the dot product between the gradient and the vector \(\(\mathbf{v}\)):
\(\(\nabla f(0, \frac{\pi}{3}) \cdot \mathbf{v} = \begin{bmatrix} \frac{7\sqrt{3}}{2} \\ \frac{7}{2} \end{bmatrix} \cdot \begin{bmatrix} -5 \\ 12 \end{bmatrix}\)\)
Using the dot product formula:
\(\(\nabla f(0, \frac{\pi}{3}) \cdot \mathbf{v} = \left(\frac{7\sqrt{3}}{2} \cdot -5\right) + \left(\frac{7}{2} \cdot 12\right)\)\)
Simplifying:
\(\(\nabla f(0, \frac{\pi}{3}) \cdot \mathbf{v} = -\frac{35\sqrt{3}}{2} + \frac{84}{2} = -\frac{35\sqrt{3}}{2} + 42\)\)
So, the directional derivative \(\(D_{\mathbf{u}} f(0 \frac{\pi}{3})\) in the direction of the vector \(\mathbf{v} = \begin{bmatrix} -5 \\ 12 \end{bmatrix}\) is \(-\frac{35\sqrt{3}}{2} + 42\).\)
To know more about derivative visit-
brainly.com/question/31422048
#SPJ11
Givien f (x) = -3x-1, solve for x when f(x) =-10
Answers
Answer:
x = 3
Step-by-step explanation:
Since both have f(x), the substitution method can be used.
1. f(x) = -3x - 1
2. f(x) = -10
Therefore,
-3x - 1 = -10
Flip to positive to calculate more easily since all are negative (although, this is optional.)
3x + 1 = 10
3x + 1 - 1 = 10 - 1 (to make one side x and other side number)
3x = 9
x = 3
Hope this helped! ^^
Consider the function. f(x) = x2 - 9, x > 3 (a) Find the inverse function of f. f-1(x) =....
Answers
the inverse function of f(x) = x^2 - 9, x > 3 is f^(-1)(x) = √(x + 9).
To find the inverse function of f(x) = x^2 - 9, x > 3, we can follow these steps:
Step 1: Replace f(x) with y: y = x^2 - 9.
Step 2: Swap x and y: x = y^2 - 9.
Step 3: Solve for y in terms of x. Rearrange the equation:
x = y^2 - 9
x + 9 = y^2
±√(x + 9) = y
Since we are looking for the inverse function, we choose the positive square root to ensure a one-to-one correspondence between x and y.
Step 4: Replace y with f^(-1)(x): f^(-1)(x) = √(x + 9).
to know more about function visit:
brainly.com/question/30721594
#SPJ11
Jessica is bringing cupcakes to school for her birthday. She is placing them in a rectangular box that can fit 4 more cupcakes long that it can wide. They will not all fit in the box, so she is also bringing a bag that can hold 12 cupcakes. The amount of cupcakes she is bringing can be represented as x(x + 4) + 12. Solve for the number of cupcakes wide and long the box will hold. Part A) What does x represent?
Answers
Answer:
the amount of cupcakes
Step-by-step explanation:
you said the amount of cupcakes can be represented by
Prove algebraically that the square of any odd number is always 1 more than a multiple of 8.
Note: Let n stand for any integer in your working
Answers
Answer: For odd n, [4n(n+1) + 1] = [4(n+1)n + 1
Step-by-step explanation: the term 4*(n+1) is always a multiple of 8, and so is [4(n+1) * n] . Thus the square of odd is yet again 1 more than some multiple of 8.
The school band needs to raise more than $16,000 to buy new uniforms. They have already raised $4,000. The need to raise the remaining amount of money over the next 6 months. Which inequality represents the amount of money, m, the school band must raise next month to purchase the uniforms?
6m + 4,000 > 16,000
6m + 4,000 <16,000
6m - 4,000 > 16,000
6m - 4,000 < 16,000
Answers
Answer:
B
Step-by-step explanation:
use function notation (with the appropriate functions above) to represent the area of a regular pentagon whose perimeter is 140 cm.
Answers
However, we need to substitute a with s since that is the value we have calculated. Therefore, we get \(A(s) = (1/4)(5 + sqrt(5))s^2.\) This is the function notation that represents the area of a regular pentagon whose perimeter is 140 cm.
Let's consider that s be the length of a side of the regular pentagon.
The perimeter of the regular pentagon will be 5s. Therefore, we have the equation:5s = 140s = 28 cm
Also,
we have the formula for the area of a regular pentagon as:
\($A=\frac{1}{4}(5 +\sqrt{5})a^{2}$,\)
where a is the length of a side of the pentagon.
In order to represent the area of a regular pentagon whose perimeter is 140 cm, we need to substitute a with s, which we have already calculated.
Therefore, we have:\(A(s) = $\frac{1}{{4}(5 +\sqrt{5})s^{2}}$\)
Now, we have successfully used function notation (with the appropriate functions above) to represent the area of a regular pentagon whose perimeter is 140 cm.
The area of a regular pentagon can be represented using function notation (with the appropriate functions above). The first step is to calculate the length of a side of the regular pentagon by dividing the perimeter by 5, since there are 5 sides in a pentagon.
In this case, we are given that the perimeter is 140 cm, so we get 5s = 140, which simplifies to s = 28 cm. We can now use the formula for the area of a regular pentagon, which is\(A = (1/4)(5 + sqrt(5))a^2\), where a is the length of a side of the pentagon.
However, we need to substitute a with s since that is the value we have calculated. Therefore, we get\(A(s) = (1/4)(5 + sqrt(5))s^2.\) This is the function notation that represents the area of a regular pentagon whose perimeter is 140 cm.
To know more about notation visit:
https://brainly.com/question/29132451
#SPJ11
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11