Answers
Answer:
AB=8cm
Step-by-step explanation:
Since ABC is a right angled triangle,
Using pythagoras theorem,
h²=p²+b²
or, BC²=AC²+AB²
or, 17²=15²+AB²
or, 289=225+AB²
or, 289-225=AB²
or, AB² = 64
so, AB=8 cm
Related Questions
5y + 10x = 0
y = - 3x
Plz help me the photo is the directions for the problem

Answers

researchers wanted to see which species of lizard (a, b, or c) is most likely to survive a bacterial infection. so they infected a total of 38 lizards and recorded how many survived after 48 hours. of the 15 species b lizards, 40% survived. for those that were species c, one more survived than died. and of the 24 lizards that died, one-third of them were species a. a. create a contingency table to display this data. (3pt) b. what proportion of the lizards in this study were either species b or c? (1pt) c. what is the probability that a species b lizard in this study did not survive? (1pt) d. are survival and being species c independent events for these lizards? justify your answer. (3pt)
Answers
a. The contingency table for the given data is attached file below.
b. The proportion of lizards that were either species A or B is 0.605.
c. The probability that a species C lizard in this study did not survive is 0.4667.
a.
The contingency table for the given data is attached file below.
b.
The proportion of lizards that were either species A or B can be calculated as:
P(A or B) = (15+8)/(15+8+6+9+4)
P(A or B) = 23/38
P(A or B) = 0.605
c.
The probability that a species C lizard in this study did not survive can be calculated as:
P(Not survive| C) = 7/15
= 0.4667
Learn more about probability here:
brainly.com/question/11234923
#SPJ4

Find the midpoint of a segment with the given endpoints.
W(-1, 1), 0(5, -5) =
Answers
Answer:
(2,-2)
Step-by-step explanation:
(5+(-1))/2=4/2=2
(-5+1)/=-4/2=-2
The Phillips curve describes the relationship between... a. The output gap and potential GDP. O b. The money supply and interest rates. C. The unemployment rate and the rate of change of wages. O d. A
Answers
The Phillips curve describes the relationship between the unemployment rate and the rate of change of wages. Option C is the correct option.
What is Phillips curve?
The relationship between the rate of inflation and the unemployment rate is represented by the Phillips curve. The analysis of wage inflation and unemployment in the United Kingdom from 1861 to 1957 by A. W. H. Phillips, despite having forerunners, is a significant development in the field of macroeconomics. When unemployment was high, wages rose slowly; when unemployment was low, wages rose quickly, according to Phillips' research.
According to Phillips' hypothesis, as the unemployment rate declines, the labor market becomes more competitive and firms are forced to raise wages more quickly in order to recruit qualified workers. The pressure decreased as unemployment rates rose. The average relationship between wage behavior and unemployment over the course of the business cycle was represented by Phillips' "curve."
To learn more about curves, click on the below link:
https://brainly.com/question/29432628
#SPJ1
Analysis of variance is used to test for equality of several population? means. standard deviations. proportions. variances.
Answers
Analysis of variance is used to test for equality of several population means.
ANOVA could also be utilized to predict the dependent variable of even more with around 2 categories and seems to be compared to the general population extra influential throughout this circumstance.
Throughout addition, ANOVA variants typically include covariates that encourage somebody to manipulate numerically for confounding factors as well as to recognize interactions wherein the factor progressives the implications of some other factor.
ANOVA (Analysis of Variance) was developed by Ronald Fisher.
ANOVA means the Analysis of Variance, is collection of statistical models & linked estimation processes, like variation among & between groups. It is used in analyzing differences among various means.
Therefore, Analysis of variance is used to test for equality of several population means.
Learn more about the ANOVA here:
https://brainly.com/question/23638404
#SPJ4
A survey conducted on a reasonably random sample of 203 undergraduates asked, among many other questions, about the number of exclusive relationships these students have been in. The histogram below shows the distribution of the data from this sample. The sample average is 3.2 with a standard deviation of 1.97. Estimate the average number of exclusive relationships Duke students have been in using a 90% confidence interval and interpret this interval in context. Check any conditions required for in- ference, and note any assumptions you must make as you proceed with your calculations and conclusions.
Answers
The average number of exclusive relationships Duke students have been in is between 2.972 and 3.428.
How to find the average number?Since the sample is reasonably random and the sample size is large enough (n > 30),Standard Error (SE) = standard deviation / sqrt(n) = 1.97 / sqrt(203) ≈ 0.138Using a t-distribution table or calculator, the critical value for a 90% confidence interval with 202 degrees of freedom is approximately 1.652.Calculate the margin of error
Margin of Error (ME) = critical value * standard error ≈ 1.652 * 0.138 ≈ 0.228Calculate the confidence interval
Lower bound: average number - margin of error = 3.2 - 0.228 ≈ 2.972
Upper bound: average number + margin of error = 3.2 + 0.228 ≈ 3.428
So, we can estimate with 90% confidence that the average number of exclusive relationships Duke students have been in is between 2.972 and 3.428.
Learn more about average number
brainly.com/question/16956746
#SPJ11
I NEED AN ANSWER ASAP PLEASE

Answers
Step-by-step explanation:
the correct answer is option a 6a-7
Write an algebraic expression for the word phrase.
10 times the product of g and h.
a. 10 (g+h)
b. 10 (g-h)
c. 10 (g/h)
d. 10gh
Answers
The answer is D) 10gh
Answer: I think the correct answer would be d
Step-by-step explanation:
determine whether the given value is a statistic or a parameter. a health and fitness club surveys 40
Answers
Any value calculated from this survey would be considered a statistic.
To determine whether the given value is a statistic or a parameter, consider the following:
A statistic is a numerical value calculated from a sample of the population, while a parameter is a numerical value that describes a characteristic of the entire population.
In this case, the health and fitness club surveys 40 members. This is a sample of the population, not the entire population.
Know more about statistic here:
https://brainly.com/question/31577270
#SPJ11
What is the common differenec in 7, 6, 5, 4,...
Answers
Answer:
d = - 1
Step-by-step explanation:
The common difference d between consecutive terms is
6 - 7 = 5 - 6 = 4 - 5 = - 1
Answer:
Step-by-step explanation:
Solve the following inequality. Graph the solution.
8a-30> 66
What is the solution? Select the correct choice below and fill in the answer box within your choice.
(Type an integer or a decimal.)
A. az
B. as
OC. a>
D. a<
Answers
The solution to the given Inequality is a > 12 and the graph is as attached.
What is the Solution to the Inequality?
We are given the Inequality as;
8a - 30 > 66
Now, use addition property of equality to add 30 to both sides to get;
8a - 30 + 30 > 66 + 30
8a > 96
Now, use division property of equality to divide both sides by 8 to get;
8a/8 > 96/8
a > 12
The graph of this is as attached.
Read more about Inequality Solution at; https://brainly.com/question/25275758
#SPJ1

Solve the equation.
–3x + 1 + 10x = x + 4
x = x equals StartFraction one-half EndFraction
x = x equals StartFraction 5 Over 6 EndFraction
x = 12
x = 18
Answers
The solution to this equation –3x + 1 + 10x = x + 4 include the following: A. x = 1/2.
How to create a list of steps and determine the solution to the equation?In order to create a list of steps and determine the solution to the equation, we would have to rearrange the variables and constants, and then collect like terms as follows;
–3x + 1 + 10x = x + 4
-3x + 10x - x = 4 - 1
6x = 3
By dividing both sides of the equation by 6, we have the following:
6x = 3
x = 3/6
x = 1/2
In conclusion, we can reasonably infer and logically deduce that solution to this equation –3x + 1 + 10x = x + 4 is 1/2 or 0.5.
Read more on solution and equation here: brainly.com/question/25858757
#SPJ1
Complete Question:
Solve the equation.
–3x + 1 + 10x = x + 4
x = 1/2
x = 5/6
x = 12
x = 18
what are the common factors of 20 and 30
A. 1,2,5,10
B. 1,2,10
C. 1,10
D. 1,5,10
Answers
Answer:
D.
Step-by-step explanation:
Its D. Bruh
initially 5 grams of salt are dissolved in 20 liters of water. brine with a concentration of 2 grams per liter is added at a rate of 3 liters a minute. the tank is mixed well and is drained at 3 liters a minute. how long does the process have to continue until there are 20 grams of salt in the tank?
Answers
The process has to continue for approximately 2.86 minutes until there are 20 grams of salt in the tank.
We can use a mass balance approach to solve this problem. Let's start by calculating the amount of salt in the tank at any given time. We know that initially there are 5 grams of salt in 20 liters of water, so the concentration of salt is:
c1 = 5 g / 20 L = 0.25 g/L
As brine with a concentration of 2 grams per liter is added at a rate of 3 liters a minute, the concentration of salt in the tank increases at a rate of:
dc/dt = 2 g/L * 3 L/min = 6 g/min
At the same time, the tank is being drained at 3 liters a minute, so the volume of the tank remains constant. This means that the total amount of salt in the tank is changing at a rate of:
dm/dt = dc/dt * V = (6 g/min) * (20 L) = 120 g/min
We want to know how long the process has to continue until there are 20 grams of salt in the tank, which means we need to solve for the time t when the total amount of salt in the tank reaches 20 grams:
m = 5 g + (6 g/min) * t - (3 L/min) * t * (0.25 g/L) = 20 g
Simplifying this equation, we get:
6t - 0.75t = 15
5.25t = 15
t = 2.86 minutes
Therefore, the process has to continue for approximately 2.86 minutes until there are 20 grams of salt in the tank.
To know more about mass balance approach click here:
brainly.com/question/14301365
#SPJ4
1/2 (2y-6) = 24
1/4 (4-y) = 10 + 24
2 (2y-3) = 4y-6
1/3 (6y-9) = 24 - 3
I think they’re linear equations but I don’t know what to do. The directions say to solve if possible??
Answers
Find formulas for the quadratic functions described below. Write your final answer in standard form. a) ...passing through the point (1,12) and whose x-intercepts are (−2,0) and (3,0). b) ...whose vertex is (3,−9) and which is passing through the point (−1,15).
Answers
The quadratic function passing through the point (1,12) and whose x-intercepts are (−2,0) and (3,0) is f(x) = 6x² - 6x - 36, The quadratic function whose vertex is (3,−9) and which is passing through the point (−1,15) is f(x) = -¼x² + (3/2)x - (9/4).
Formula for the quadratic function passing through the point (1,12) and whose x-intercepts are (−2,0) and (3,0) can be obtained as follows:
Using the x-intercepts to get the factors of the quadratic function: f(x) = a(x + 2)(x - 3).
Since the graph passes through (1, 12), we can substitute these coordinates to get a value for the coefficient a:12 = a(1 + 2)(1 - 3)12 = -6a6 = aTherefore, the formula for the quadratic function is:f(x) = 6(x + 2)(x - 3).
The answer is = 6(x + 2)(x - 3)To write this in standard form, we need to multiply out the brackets:f(x) = 6(x² - x - 6)f(x) = 6x² - 6x - 36.
The final answer in standard form is f(x) = 6x² - 6x - 36.b) The formula for the quadratic function whose vertex is (3,−9) and which is passing through the point (−1,15) can be obtained as follows:
Using the vertex form of a quadratic function:f(x) = a(x - h)² + k, where (h, k) is the vertex of the parabola.Substitute the coordinates of the vertex to get:f(x) = a(x - 3)² - 9We still need to find the value of a.
To do this, we can use the point (-1, 15) that the parabola passes through:15 = a(-1 - 3)² - 915 = 16a24a = -6a = -¼Substitute a into the equation:f(x) = -¼(x - 3)² - 9.
The answer f(x) = -¼(x - 3)² - 9.
To write this in standard form, we need to multiply out the brackets and simplify:f(x) = -¼(x² - 6x + 9) - 9f(x) = -¼x² + (3/2)x - (9/4)The final answer in standard form is f(x) = -¼x² + (3/2)x - (9/4).
In conclusion, the quadratic function passing through the point (1,12) and whose x-intercepts are (−2,0) and (3,0) is f(x) = 6x² - 6x - 36, whereas, the quadratic function whose vertex is (3,−9) and which is passing through the point (−1,15) is f(x) = -¼x² + (3/2)x - (9/4).
To know more about quadratic function visit:
brainly.com/question/27958964
#SPJ11
PLEASE HELP ME! I will mark you as BRAINLIEST if you answer this correctly.

Answers
Answer:
0.92
Step-by-step explanation:
Each year, the value declines. This eliminates choices A and D.
The decline from 33000 to 30360 is slightly less than 10%, so the multiplier from one year to the next is slightly more than 1 -10% = 90%. The only choice in range is ...
0.92 . . . . the third listed choice
The quotient of a number w and five is at most four.
Answers
Answer:
b =345
Step-by-step explanation:
The solution is w ≤ 20
The inequality equation is w ≤ 20
What is an Inequality Equation?Inequalities are the mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
In an inequality, the two expressions are not necessarily equal which is indicated by the symbols: >, <, ≤ or ≥.
Given data ,
Let the inequality equation be represented as A
Now , the value of A is
Let the number be w
A = quotient of a number w and five is at most four
Substituting the values in the equation , we get
w / 5 ≤ 4 be equation (1)
Multiply by 5 on both sides of the equation , we get
w ≤ ( 4 x 5 )
w ≤ 20
Therefore , the value of A is w ≤ 20
Hence , the inequality equation is w ≤ 20
To learn more about inequality equations click :
https://brainly.com/question/11713066
#SPJ2
Assume the given general functional form; what is Y in the following linear regression? Y=α0+α1×1+α2×2+ε error term/residual intercept dependent variable independent variable
Answers
Y in represents the following in this linear regression Y = α₀+α₁X+α₂X₂+ε: C. dependent variable.
What is a regression line?In Mathematics and Geometry, a regression line is a statistical line that best describes the behavior of a data set. This ultimately implies that, a regression line simply refers to a line which best fits a set of data.
In Mathematics and Geometry, the general functional form of a linear regression can be modeled by this mathematical equation;
Y = α₀+α₁X+α₂X₂+ε
Where:
Y represent the dependent variable.x represent the independent variable.ε represent the error term or residualα₀ represent the intercept or initial value.In conclusion, Y represent the dependent variable or response variable in a linear regression.
Read more on linear regression here: brainly.com/question/16793283
#SPJ1
there are 2 senators from each of tahe 50 states. we wish to make a 3 senator committe in which no two how many ways can ewe choose a senator from a chosen state
Answers
There are 3 ways to select a senator from a state if you wish to make a 3-senator committee in which no two senators are from the same state.
There are two senators from each of the 50 states, we wish to create a committee of three senators so that no two senators are from the same state.
Therefore, there are three different ways to choose a senator from a particular state, because we have to pick one out of two senators to ensure that no two senators are from the same state.For example, if we choose a senator from the state of New York, we can pick 1 senator from New York and then select 2 senators from the remaining 98 senators, giving us 298 ways to pick 2 senators.Therefore, the total number of ways to choose a 3-senator committee is: 2 C 98 + 3 = 2,941 ways.
To learn more about “senator” refer to the https://brainly.com/question/25132339
#SPJ11
Help ASAP will give 20 points!!!!!
use six unit multipliers to convert 33 cubic feet to cubic centimeters
Answers
Converting 33 cubic feet to cubic centimeters would give 934454. 4 cubic centimeters
How to determine the conversionIt is important to note that conversion of units requires the appropriate equivalent values
For
I cubic foot is equivalent to 28316. 8 cubic centimeters
But we were given
33 cubic feet for the conversion
If 1 cubic foot = 28316. 8 cubic centimeters
Then 33 cubic feet = x
Cross multiply, we get
x = 28316. 8 × 33
x = 934454. 4 cubic centimeters
Thus, converting 33 cubic feet to cubic centimeters would give 934454. 4 cubic centimeters
Learn more about conversion factor here:
https://brainly.com/question/17748772
#SPJ1
Algo (Inferences About the Difference Between Two Population Means: Sigmas Unknown) Question 4 of 13 Hint(s) The U.S. Department of Transportation provides the number of miles that residents of the 75 largest metropolitan areas travel per day in a car. Suppose that for a random sample of 70 Buffalo residents the mean is 22.5 miles a day and the standard deviation is 8.5 miles a day, and for an independent random sample of 40 Boston residents the mean is 18.2 miles a day and the standard deviation is 7.1 miles a day. Round your answers to one decimal place. a. What is the point estimate of the difference between the mean number of miles that Buffalo residents travel per day and the mean number of miles that Boston residents travel per day? O b. What is the 95% confidence interval for the difference between the two population means? to
Answers
The point estimate of the difference between the mean number of miles that Buffalo residents travel per day and the mean number of miles that Boston residents travel per day is 4.3 miles/day. The 95% confidence interval for the difference between the two population means is (2.08, 6.52) miles/day.
a)
The point estimate of the difference between the mean number of miles that Buffalo residents travel per day and the mean number of miles that Boston residents travel per day can be calculated as:
Point estimate = Mean of Buffalo residents - Mean of Boston residents
Point estimate = 22.5 miles/day - 18.2 miles/day
Point estimate ≈ 4.3 miles/day
Therefore, the point estimate of the difference between the mean number of miles that Buffalo residents travel per day and the mean number of miles that Boston residents travel per day is 4.3 miles/day.
b)
To calculate the 95% confidence interval for the difference between the two population means, we can use the formula:
Confidence interval = (Point estimate) ± (Critical value) * (Standard error)
The critical value depends on the desired confidence level and the sample size. Since the sample sizes are relatively large (70 and 40), we can approximate the critical value using a Z-distribution.
For a 95% confidence level, the critical value for a two-tailed test is approximately 1.96.
The standard error can be calculated as:
Standard error = sqrt((s1^2 / n1) + (s2^2 / n2))
where s1 and s2 are the sample standard deviations, and n1 and n2 are the sample sizes.
Standard error = sqrt((8.5^2 / 70) + (7.1^2 / 40))
Standard error ≈ 1.1307
Now, we can calculate the confidence interval:
Confidence interval = 4.3 ± 1.96 * 1.1307
Confidence interval ≈ (2.08, 6.52)
Therefore, the 95% confidence interval for the difference between the two population means is (2.08, 6.52) miles/day.
To learn more about mean: https://brainly.com/question/1136789
#SPJ11
-4(10-a)=36 what the steps
Answers
Hey there!☺
\(Answer:\boxed{a=19}\)
\(Explanation:\)
\(-4(10-a)=36\) Equation
−4(10 − a) = 36 Simplify both sides
(−4)(10) + (−4)(−a) = 36 Distribute
−40 + 4a = 36
4a − 40 = 36
4a - 40 + 40 = 36 + 40 Add 40 to both sides
4a = 76
4a/4 = 76/4 Divide both sides by 4
76/4 = 19 Simplify 76/4
a = 19
Hope this helps!
Ayuden por favor, no entiendo este problema

Answers
We will get that the angle theta is:
θ = β/2
How to find the value of theta?Remember that the sum of the interior angles of any triangle must be equal to 180°.
Now, looking at the triangle in the left, we can see that the top angle is equal to:
180 - 2α
The right angle is equal to:
180 - 2β
And the left angle is α
Then we can write:
α + (180 - 2α) + (180 - 2β) = 180
-α - 2β = -180
α = 180 - 2β
Now we can go to the other triangle, where theta is, and write:
α + β + 2θ = 180
Replacing what we found above, we get:
180 - 2β + β + 2θ = 180
-β + 2θ = 0
θ = β/2
That is the best simplification we can get with the given diagram.
Learn more about interior angles at:
https://brainly.com/question/24966296
#SPJ1
What is the coefficient of the third term in the binomial expansion of (a + b)6? 1 15 20 90
Answers
Answer: 15
Step-by-step explanation:
(r+1)th term of \((a+b)^n\) is given by:-
\(T_{r+1}=\ ^nC_r(a)^{n-r}b^r\)
For \((a+b)^6\) , n= 6
\(T_3=T_{2+1}=\ ^6C_2(a)^{6-2}(b)^2\\\\\)
\(=\ \dfrac{6!}{4!2!}a^4b^2\ \ \ [^nC_r=\dfrac{n!}{r!(n-r)!}]\\\\=\dfrac{6\times5\times4!}{4!\times2}a^4b^2\\\\=3\times5a^4b^2\\\\ =15a^4b^2\)
Hence, the coefficient of the third term in the binomial expansion of \((a+b)^6\) is 15.
Answer:
15
Step-by-step explanation:
Theoretical Probability and Random Processes. If you could please provide a detailed answer I will be sure to upvote. Thank you in advanced. 14. Ascertain in the following cases whether or not F is the joint distribution function of some pair (X, Y) of random variables. If your conclusion is affirmative, find the distribution functions of X and Y separately. 1-e-x-y if x,y0, F(x,y) 0 otherwise. 1-e-x=xe-y if0x y, F(x,y)= 1-e-y-ye-y if0yx, 0 otherwise. (a) (b)
Answers
1. the distribution function of X is \(F_X(x)\) = 1 - \(e^{-x\) for x ≥ 0, and the distribution function of Y is \(F_Y(y)\) = 1 for y ≥ 0.
2. The function F(x, y) is not the joint distribution function of any pair (X, Y) of random variables.
Let's analyze each case separately:
(a) F(x, y) = 1 - \(e^{-x - y\) if x, y ≥ 0, and F(x, y) = 0 otherwise.
To determine if F is the joint distribution function of some pair (X, Y) of random variables, we need to check if F satisfies the properties of a distribution function:
1. Non-negativity: F(x, y) ≥ 0 for all (x, y).
2. Monotonicity: F(x, y) is non-decreasing in both x and y.
3. Right-continuity: F(x, y) is right-continuous in both x and y.
4. Marginal distribution: The marginal distribution functions, \(F_X(x)\) and \(F_Y(y)\), can be obtained by integrating F(x, y) over the respective variables.
In this case, the function F(x, y) satisfies the properties of a distribution function:
1. Non-negativity: F(x, y) = 1 - \(e^{-x - y\) ≥ 0 for all x, y ≥ 0.
2. Monotonicity: The partial derivatives of F(x, y) with respect to x and y are non-negative for x, y ≥ 0, which implies that F(x, y) is non-decreasing in both x and y.
3. Right-continuity: The function F(x, y) is continuous for all x, y ≥ 0.
4. Marginal distribution: To find the marginal distribution functions, we can integrate F(x, y) over the respective variables.
Let's find the distribution functions of X and Y separately:
\(F_X(x)\) = ∫[0 to ∞] F(x, y) dy
= ∫[0 to ∞] (1 - \(e^{-x - y\)) dy
= [y - \(e^{-x - y\)]|[0 to ∞]
= ∞ - (0 - \(e^{-x - 0\))
= 1 - e\(e^{-x\)
\(F_Y(y)\) = ∫[0 to ∞] F(x, y) dx
= ∫[0 to ∞] (1 - \(e^{-x - y\)) dx
= [x - \(e^{-x - y\)]|[0 to ∞]
= ∞ - (0 - \(e^{-\infty - y\))
= 1
Therefore, the distribution function of X is \(F_X(x)\) = 1 - \(e^{-x\) for x ≥ 0, and the distribution function of Y is \(F_Y(y)\) = 1 for y ≥ 0.
(b) F(x, y) = 1 - \(e^{-x\) = x \(e^{ - y\) if 0 ≤ x ≤ y, and F(x, y) = 0 otherwise.
Let's analyze this case using the same criteria:
1. Non-negativity: F(x, y) = 1 - \(e^{-x\) = x \(e^{- y\) ≥ 0 for 0 ≤ x ≤ y.
2. Monotonicity: The partial derivatives of F(x, y) with respect to x and y are positive for 0 ≤ x ≤ y, indicating that F(x, y) is increasing in both x and y.
3. Right-continuity: F(x, y) is continuous for 0 ≤ x ≤ y.
4. Marginal distribution: We need to find the marginal distribution functions \(F_X(x)\) and \(F_Y(y)\) by integrating F(x, y) over the respective variables.
Let's find the distribution functions of X and Y separately:
\(F_X(x)\) = ∫[x to ∞] F(x, y) dy
= ∫[x to ∞] (1 - \(e^{-x\)) dy
= (y - \(e^{-x\) y)|[x to ∞]
= ∞ - (x - \(e^{-x\) x)
= 1 - x \(e^{-x\) for x ≥ 0
\(F_Y(y)\) = ∫[0 to y] F(x, y) dx
= ∫[0 to y] (1 - \(e^{-x\) y \(e^{- y\)) dx
= (x -\(e^{-x\) x \(e^{- y\))|[0 to y]
= y -\(e^{- y\) y \(e^{- y\)
= y(1 - \(e^{ - y\)) for y ≥ 0
Therefore, the distribution function of X is F_X(x) = 1 - x \(e^{-x\) for x ≥ 0, and the distribution function of Y is \(F_Y(y)\) = y(1 - \(e^{- y\)) for y ≥ 0.
Learn more about distribution function here
https://brainly.com/question/30402457
#SPJ4
help please thank you
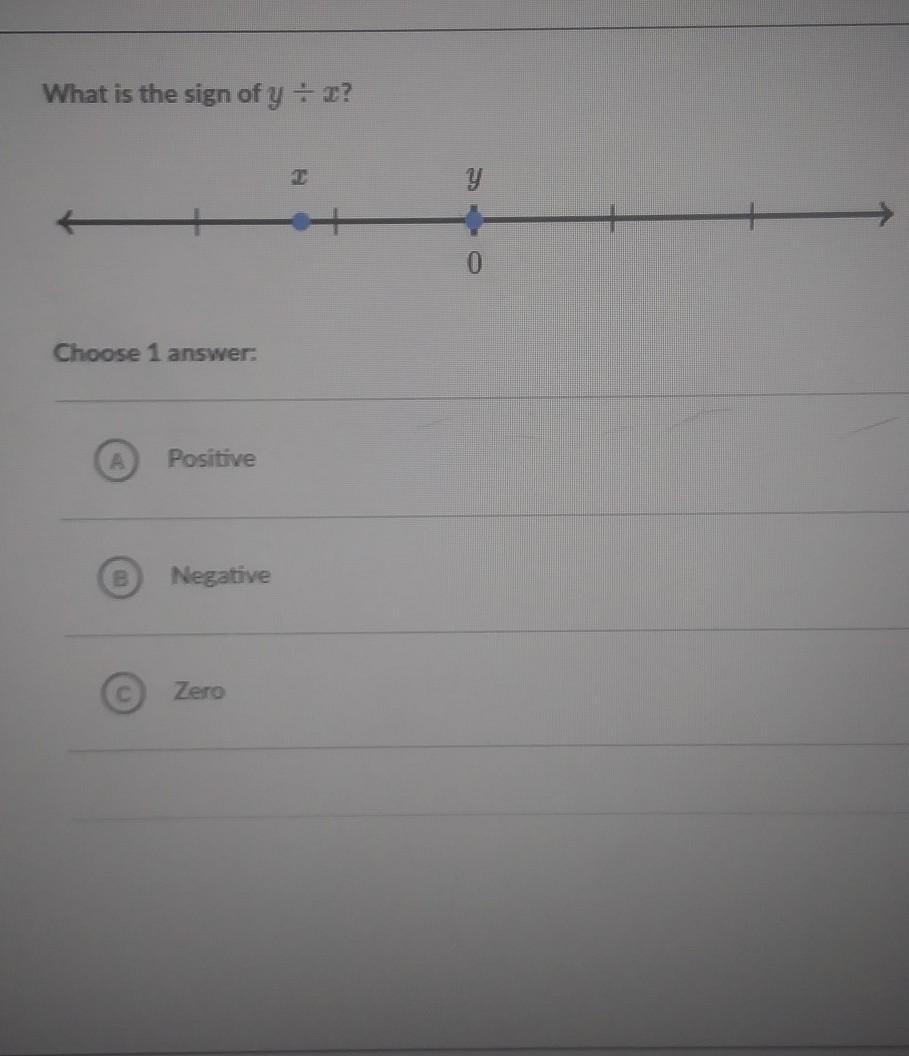
Answers
Answer:
Negative:)
Step-by-step explanation:
Kevin spent $14.00 of the $25.00 in her wallet. Which decimal represents the fraction of the $25.00 Kevin spent?
Answers
Answer:
0.56
Step-by-step explanation:
14/25 = 14×4/25×4
=56/100
=0.56
Select the correct answer.
Using synthetic division, find (2x + 4x³ + 2x² + 8x + 8) + (x + 2).
O A. 2x3 + 2x + 4
OB.
2x4 + 2x² + 4x
OC. 2x3 + 2x + 4 +
I
OD.
2x3 + 2x² + 4
1
+ 2

Answers
The synthetic division of the polynomial, (2x⁴ + 4x³ + 2x² + 8x + 8) / (x + 2) = 2x³ + 2x + 4.
Division of the polynomialThe division of the polynomial is determined as follows;
(2x⁴ + 4x³ + 2x² + 8x + 8) / (x + 2)
2x³ + 2x + 4
-------------------------
x + 2 √(2x⁴ + 4x³ + 2x² + 8x + 8)
- (2x⁴ + 4x³)
-------------------------------------
2x² + 8x + 8
- (2x² + 4x)
------------------------
4x + 8
- (4x + 8)
-------------------
0
Thus, the synthetic division of the polynomial, (2x⁴ + 4x³ + 2x² + 8x + 8) / (x + 2) = 2x³ + 2x + 4.
Learn more about synthetic division here: https://brainly.com/question/24662212
#SPJ1
Jennie has a jar containing 800 mL of wax that she uses to make candles for her school project. She uses 50 mL of wax from the jar to make one candle.
The function A(n)=800−50n represents the amount of wax left in the jar after making n candles.
What is the domain of the function A(n) in this context?
Answers
The domain of the function A(n) which represents the amount of wax left in the jar after making candles is; n = {n: 0<= n <= 16}.
What is the Domain of the function given in which case 800mL of wax is used to make candles according to the function?According to the task content, it follows that tge function given to represent the use of wax to make candles is;
A(n)=800−50n
Hence, since the domain of a function is the set of all possible values of n, it follows that the possible values of n spans from the least to the highest as follows;
When none of the wax is used for candles;
800 = 800 -50n.
0 = -50n
n = 0.
When all of the wax is used for candles;
0 = 800 - 50n
-800 = -50n
n = 16.
Read more on domain of a function;
https://brainly.com/question/1942755
#SPJ1
