Find the Inverse f(x) = 5x3+ 5 1-6 f(x) = 10x 3 - 6 f(x) = 3x - 11 (x) = 2+1 f(x) = log2 (x+1) - 3 $(1) 5x $(x) =5/*+1 f(x) =(x + 2)2-5
Answers
The inverse function is f^(-1)(x) = -2 ± sqrt(x + 5).
To find the inverse of a function, we need to interchange the roles of x and y and solve for y.
For f(x) = 5x^3 + 5:
Interchanging x and y: x = 5y^3 + 5
Solving for y:
5y^3 = x - 5
y^3 = (x - 5) / 5
y = ((x - 5) / 5)^(1/3)
So, the inverse function is f^(-1)(x) = ((x - 5) / 5)^(1/3).
For f(x) = 10x^3 - 6:
Interchanging x and y: x = 10y^3 - 6
Solving for y:
10y^3 = x + 6
y^3 = (x + 6) / 10
y = ((x + 6) / 10)^(1/3)
So, the inverse function is f^(-1)(x) = ((x + 6) / 10)^(1/3).
For f(x) = 3x - 11:
Interchanging x and y: x = 3y - 11
Solving for y:
3y = x + 11
y = (x + 11) / 3
So, the inverse function is f^(-1)(x) = (x + 11) / 3.
For f(x) = 2^(x + 1) - 3:
Interchanging x and y: x = 2^(y + 1) - 3
Solving for y:
2^(y + 1) = x + 3
y + 1 = log2(x + 3)
y = log2(x + 3) - 1
So, the inverse function is f^(-1)(x) = log2(x + 3) - 1.
For f(x) = (x + 2)^2 - 5:
Interchanging x and y: x = (y + 2)^2 - 5
Solving for y:
x = y^2 + 4y + 4 - 5
x = y^2 + 4y - 1
Rearranging the equation: y^2 + 4y - (x + 1) = 0
Using the quadratic formula, we can solve for y:
y = (-4 ± sqrt(16 + 4(x + 1))) / 2
y = (-4 ± sqrt(4x + 20)) / 2
Simplifying further: y = -2 ± sqrt(x + 5)
So, the inverse function is f^(-1)(x) = -2 ± sqrt(x + 5).
Learn more about inverse function at https://brainly.com/question/13671128
#SPJ11
Related Questions
(t+8)^3
i want you to solve this
Answers
\(( {t + 8})^{3} = {t}^{3} + 3 \times ({t})^{2} \times( 8) + 3 \times (t) \times ( {8})^{2} + {8}^{3} \\ \)
So :
\( ({t + 8})^{3} = {t}^{3} + 24 {t}^{2} + 192t + 512\)
5. Find mZFOE
35
55
70
110
(1 point)
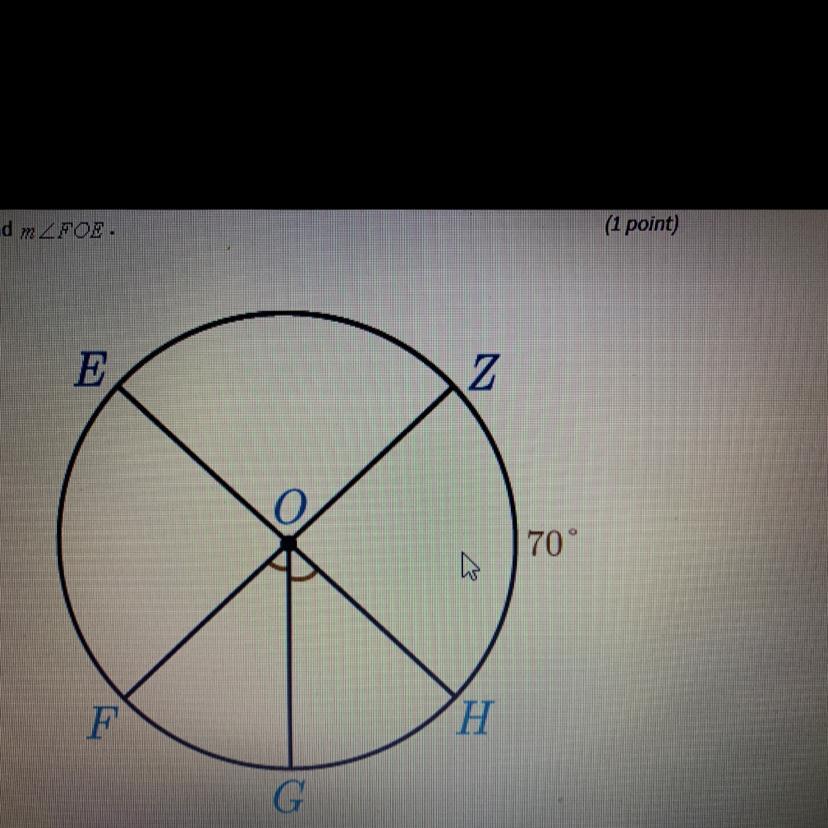
Answers
Answer:
your answer to this question is 35
Which of the following is a degenerate circle?
O A. x++y2 = -1
O B. x+y=2
O c. x² + y2 = 1
O D. (x – 4)+ (x - 2)2 = 0

Answers
I need help on these!

Answers
Three points that are solutions to the system are:
(0, -9)
(3, -5)
(4, -4)
b.
Three points that are solutions to the system are:
(3, 2)
(2, 1)
(1, 0)
The gradient of the curve y = ax² + bx at the point (3, 3) is 4. Find the value of a and the value of b.
Answers
The curve passes through the point (3, 3), so \(y=3\) when \(x=3\). Then
\(y = ax^2 + bx \implies 3 = 9a + 3b \implies 3a + b = 1\)
The tangent line to the curve at (3, 3) has gradient \(\frac{dy}{dx}\) at \(x=3\). Compute the derivative.
\(y = ax^2 + bx \implies \dfrac{dy}{dx} = 2ax + b\)
Then when \(x=3\), the gradient is 4, so
\(2ax + b = 4 \implies 6a+b=4\)
Solve for \(a\) and \(b\). Eliminating \(b\), we find
\((6a+b) - (3a+b) = 4-1 \implies 3a = 3 \implies \boxed{a=1}\)
and it follows that
\(3 + b = 1 \implies \boxed{b = -2}\)
Mrs. Stokes solved the equation shown below. Select the correct justification for each step shown.
-3(8x-2)=9-21x Original equation
8x-2=-3+7x
8x+1=7x
1=-x
-1=x
Answers
Answer:
Below in bold
Step-by-step explanation:
-3(8x - 2) = 9 - 21x
~Divide -3 to everything
8x - 2 = -3 + 7x
~Add 3 to both sides
8x + 1 = 7x
~Subtract 8x to both sides
1 = -x
~Divide -1 to both sides
-1 = x
Note that this isn't the most used way to solve equations because you would typically use distribution to simplify the left side.
Best of Luck!
Below in bold
Step-by-step explanation:
-3(8x - 2) = 9 - 21x
~Divide -3 to everything
8x - 2 = -3 + 7x
~Add 3 to both sides
8x + 1 = 7x
~Subtract 8x to both sides
1 = -x
~Divide -1 to both sides
-1 = x
Note that this isn't the most used way to solve equations because you would typically use distribution to simplify the left side.
Best of Luck!
In statistics, if a p-value is less than an alpha set at 0.05, is it considered significant or not?
Answers
A p-value less than 0.05 is considered significant because it indicates strong evidence against the null hypothesis.
A p-value is a measure of the strength of evidence against a null hypothesis. It tells you the probability of getting a test statistic as extreme as the one you observed, assuming the null hypothesis is true.
Now, to answer your question, if a p-value is less than an alpha set at 0.05, it is considered significant. This means that there is less than a 5% chance that the observed effect is due to random chance or error.
In other words, the evidence is strong enough to reject the null hypothesis and support the alternative hypothesis.
To better understand this concept, let's consider an example. Suppose we want to test whether a new drug is effective in treating a certain condition.
The null hypothesis is that the drug has no effect, while the alternative hypothesis is that it does have an effect. We conduct a clinical trial with a sample size of 100 patients and find that 60 of them show improvement after taking the drug.
We calculate a p-value of 0.02, which is less than our alpha of 0.05. This means that there is strong evidence to reject the null hypothesis and conclude that the drug is indeed effective.
To know more about p-value here.
https://brainly.com/question/30461126
#SPJ4
What type of solution does this equation have? *
4x + 8 = 4x + 8
no solution
one solution
infinite many solutions
Answers
Answer:
Infinite solutions
Step-by-step explanation:
4x + 8 = 4x +8
Both sides are exactly the same, so there are infinite solutions.
The formula for the area of a circle is A= πr² . Solve the equation for r . If the area of a circle is 78.5 cm² , what is the radius? Use 3.14 for π .
Answers
The radius of the circle with an area of 78.5 cm² is 5 cm.
To solve the equation A = πr² for r, we need to isolate the variable r on one side of the equation. Let's do the calculations:
A = πr²
78.5 = 3.14r²
To solve for r, we need to divide both sides of the equation by π:
78.5/3.14 = r²
Simplifying the left side of the equation gives us:
25 = r²
To find the value of r, we can take the square root of both sides of the equation:
√25 = √(r²)
5 = r
Therefore, the radius of the circle with an area of 78.5 cm² is 5 cm.
To know more about area click-
http://brainly.com/question/16519513
#SPJ11
with steps please
A student uses a clinometer to measure the angle of elevation of a sign that marks the point on a tower that is 45 m above the ground. The angle of elevation is 32° and the student holds the clinometer 1.3 m above the ground. He then measures the angle of elevation of the top of the tower as 47º. Sketch and label a diagram to represent the information in the problem. Determine the height of the tower to the nearest tenth of a metre
Answers
Answer: \(75\ m\)
Step-by-step explanation:
Given
The tower is 45 m high and Clinometer is set at 1.3 m above the ground
From the figure, we can write
\(\Rightarrow \tan 32^{\circ}=\dfrac{43.7}{x}\\\\\Rightarrow x=\dfrac{43.7}{\tan 32^{\circ}}\\\\\Rightarrow x=69.93\ m\)
Similarly, for \(\triangle ACD\)
\(\Rightarrow \tan 47^{\circ}=\dfrac{43.7+y}{x}\\\\\Rightarrow 69.93\times \tan 47^{\circ}=43.7+y\\\\\Rightarrow 74.99=43.7+y\\\Rightarrow y=31.29\ m\)
Height of the tower is \(43.7+31.29\approx 75\ m\)

Simplify by using the laws of indices: 3(112 m^11 n^-2) ÷ (672 m^3 n^2)
Answers
Answer:
(m^8)/(2n^4)
Step-by-step explanation:
The relevant laws of indices are ...
(a^b)/(a^c) = a^(b-c)a^-b = 1/a^b__
Simplifying the given expression using these rules gives ...
\(3\dfrac{112m^{11}n^{-2}}{672m^3n^2}=\dfrac{336}{672}m^{11-3}n^{-2-2}=\boxed{\dfrac{m^8}{2n^4}}\)
2
A math teacher observed that as the number of hours students studied their multiplication facts increased, the
number of errors the students made on their multiplication tests decreased. Which scatterplot could support this
teacher's observation?
F
G
Number of Errors
Number of Errors
10
0
y
10
0
Multiplication Tests
12 3 4
Study Time (hours)
Multiplication Tests
1 2 3 4
Study Time (hours)
5
H
J
Number of Errors
Number of Errors
10
2
10
Multiplication Tests
2
●
0 1 2 3 4
Study Time (hours)
Multiplication Tests
●
0 1 2 3 4
Study Time (hours)
5
Answers
A scatterplot that shows the number of hours studied on the x-axis and the number of errors on the y-axis would best support the teacher's observation.
What is error in math?Error in math is an incorrect answer to a mathematical equation or problem. It can be caused by a variety of factors, such as inaccurate calculations, misreading instructions, or not understanding the problem. Error in math can be frustrating and can lead to poor grades, but it can also be an opportunity for learning and growth. With the proper guidance and understanding, students can learn from their mistakes and become better mathematicians.
The scatterplot would likely show a negative correlation, with the number of errors decreasing as the number of hours studied increases. This indicates that as students study more, their performance on multiplication tests improves. It could also show an outlier or two, which could indicate that some students are able to learn multiplication facts more quickly than others.
To know more about error click-
https://brainly.com/question/28001423
#SPJ1
4x - 3 = 2x + 7
what’s the value of x
Answers
Answer:
x = 5
Step-by-step explanation:
4x - 3 = 2x + 7
Add 3 to both sides.
4x = 2x + 10
Subract 2x from both sides.
2x = 10
Divide both by 2.
Final Answer: 5
If you wanted to check your answer, you can plug in 5 from the x's
4(5) - 3 = 2(5) + 7
17 = 17
Answer: X = 5
Step-by-step explanation: The target should be to reduce the equations to having either one term or polynomial on each side, starting with the right side. First, start with subtracting 2x from each side. Then, add three to both sides. Finally, divide both sides. You can also double-check the answer by substituting.
4x - 3 = 2x + 7
2x - 3 = 7 (Subtracted 2x)
2x = 10 (Added 3 to both sides)
10/2 (Divide both sides)
X = 5
4(5) - 3 = 2(5) + 7
17 = 17
The graph of a line has slope 3/2 and passes through the point (-2, 4). Which point is on this line?
(0, 7)
(1, 6)
(2, 11)
(4, 1)
Answers
Answer:
(2, 11)
Step-by-step explanation:
Answer:
(1, 6)
Step-by-step explanation:
Define a relation R on Z as xRy if and only if x^2+y^2 is even. Prove R is an equivalence relation. Describe its equivalence classes.
Answers
A relation R on Z is an equivalence relation if and only if it is reflexive, symmetric, and transitive. Specifically, in this case, xRy if and only if x^2+y^2 is even.
Reflexive: for any x in Z, x^2+x^2 is even, thus xRx. So, R is reflexive.
Symmetric: for any x,y in Z, if xRy, then x^2+y^2 is even, which implies y^2+x^2 is even, thus yRx. So, R is symmetric.
Transitive: for any x,y,z in Z, if xRy and yRz, then x^2+y^2 and y^2+z^2 are both even, thus x^2+z^2 is even, thus xRz. So, R is transitive.
Therefore, R is an equivalence relation.
To describe the equivalence classes, we need to find all the integers that are related to a given integer x under the relation R.
Let [x] denote the equivalence class of x.
For any integer x, we can observe that xR0 if and only if x^2 is even, which occurs when x is even.
Therefore, every even integer is related to 0 under R, and we have:[x] = {y in Z: xRy} = {x + 2k: k in Z}, for any even integer x.
Similarly, for any odd integer x, we can observe that xR1 if and only if x^2 is odd, which occurs when x is odd. Therefore, every odd integer is related to 1 under R, and we have:[x] = {y in Z: xRy} = {x + 2k: k in Z}, for any odd integer x.
In summary, the equivalence classes of R are of the form {x + 2k: k in Z}, where x is an integer and the parity of x determines whether the class contains all even or odd integers.
Learn more about equivalence class and equivalence relation here, https://brainly.com/question/15286301
#SPJ11
pls help gsoehehsjbsgshsjbsfeoanevshksnevehwknsbdgsknwbsgdindvegshsn

Answers
Answer:
a) 5.9
b) 4.2
Step-by-step explanation:
Plot the data points on the number line (see attached).
Part (a)
\(\begin{aligned}\textsf{Distance between Ben and Kloee} & = \sf \left| Ben - Kloee \right|\\& = \sf \left|-2.65-3\frac{1}{4}\right|\\& = \sf \left|-2.65-3.25\right|\\& = \sf \left|-5.9\right|\\& = \sf 5.9\end{aligned}\)
Part (b)
\(\begin{aligned}\textsf{Distance between Middle school and Football field} & = \sf \left| Middle\:school-Football\:field\right|\\& = \sf \left| 1.5-5.7\right|\\& = \sf \left| -4.2 \right|\\& = \sf 4.2\end{aligned}\)

0.9-8.8+11+2.6 es tarea de matemáticas
Answers
Resolviendo las sumas y restas de la expresión podemos ver que:
0.9-8.8+11+2.6 = 5.7
¿Como resolver la expresión en la imagen?
Tenemos un problema que involucra sumas y restas, tenemos que resolver la siguiente expresión:
0.9-8.8+11+2.6
Vamos a hacerlo de izquierda a derecha, lo primero que debemos resolver es:
0.9 - 8.8 = -7.9
reemplazar esto nos da:
-7.9+11+2.6
Lo siguiente que debemos resolver es:
-7.9 +11 = 3.1
Reemplazando eso obtenemos:
3.1 + 2.6 = 5.7
ese es el resultado de la expresion.
Entonces podemos concluir que:
0.9-8.8+11+2.6 = 5.7
Sí quieres aprender más sobre expresiones matematicas puedes leer:
https://brainly.com/question/723406
#SPJ1
Find the limit, if it exists, or show that the limit does not exist. lim(,)→(0,0) 2 2 4
Answers
The limit does not exist.
What is a limit?A limit in mathematics is the value that a function approaches when its input approaches some value. Limits are used to define continuity, derivatives, and integrals in calculus and mathematical analysis.In order for such a limit to occur, the fraction \(\frac{x^{2} }{x^{2} +y^{2} }\) must be comparable to the same value \(L\), regardless of the way we take to get there \((0,0)\).
Try approaching \((0,0)\) along the x-axis.
This means setting \(y=0\) and finding the limit \(lim_{x-0} \frac{x^{2} }{x^{2} +y^{2} }\).
We obtain:
\(lim_{x-0,y=0}\frac{x^{2} }{x^{2} +y^{2} } =lim_{y=0}}\frac{x^{2} }{x^{2} +0 }\\=lim_{x-0}} \frac{x^{2} }{x^{2} } \\\\=lim_{x-0}}1\\=1\)
Now evaluate approaching \((0,0)\) along the y-axis.
This means setting \(x=0\) and finding the limit \(lim_{y-0} \frac{x^{2} }{x^{2} +y^{2} }\).
\(lim_{y-0,x-0} \frac{x^{2} }{x^{2} +y^{2} } =lim_{y-0} \frac{0}{0+y^{2} } \\=lim_{y-0} \frac{0}{y^{2} } \\=lim_{y-0} 0\\=0\)
Approaching the origin via these two methods results in distinct limits.
\(lim_{x-0,y-0} \frac{x^{2} }{x^{2} +y^{2} }\) ≠ \(lim_{y-0,x-0}\frac{x^{2} }{x^{2} +y^{2} }\)
Therefore the limit does not exist.
Know more about limits here:
https://brainly.com/question/1521191
#SPJ4
The correct question is given below:
Find the limit, if it exists, or show that the limit does not exist.
\(lim_{(x,y) -(0,0)} \frac{x^{2} }{x^{2} +y^{2} }\)
What is the slope of the graph of this function in decimal form?
(6,1) (-6,-5)
Answers
Answer:
slope = 0.5
Step-by-step explanation:
\(slope=\frac{-5-1}{-6-6} =\frac{-6}{-12} =\frac{1}{2} =0.5\)
Hope this helps
The slope of the graph through points (6,1) and (-6,-5) is 0.5.
What is the slope of the graph?The slope formula can be expressed as:
\(Slope (m) = \frac{y_2 - y_1}{x_2 - x_1}\)
Given the coordinates of the points through which the graph passes through:
Point 1 ( 6,1 )
x₁ = 6
y₁ = 1
Point 2( -6,-5 )
x₂ = -6
y₂ = -5
Plug the coordinates into the slope formula and simplify.
\(Slope (m) = \frac{y_2 - y_1}{x_2 - x_1}\\\\Slope (m) = \frac{-5 - 1}{-6 - 6}\\\\Slope (m) = \frac{-6}{-12}\\\\Slope (m) = \frac{1}{2}\\\\Slope (m) = 0.5\)
Therefore, the slope of the line is 0.5.
Learn more about slope formula here: brainly.com/question/24578307
#SPJ3
You owe $1,032.56 on a credit card with an 11.25% APR. The minimum due is $67.00
and you pay it at the beginning of the month. How much interest is accrued by the end of the month?
Answers
Interest accrued at the end of the month is $1.41.
What is the interest on credit card?Credit cards impose interest on any sums that you don't pay by the due date each month. Interest accrues everyday when you hold a balance from month to month based on the so-called Daily Periodic Rate (DPR). DPR is only another term for your daily interest charge.
Step 1: Make the initial payment of $882 ($1,032 - $150).
Step 2: $882 times 1.00938 is $890.27
Step 3: Pay $1,032 multiplied by 1.00938 ($1,041.68) at the conclusion.
Step 4. $1,041.68 - $150= $891.68
The interest for the first month is $1.41.
To learn more about interest on credit card from given link
https://brainly.com/question/24267737
#SPJ9
Please help please. P

Answers
the answer is b, 7/25
1, 3, 4, 7, 11, 18, ,
What is the pattern?
Answers
Answer:
I think its Fibonacci numbers.
Answer:
29
Step-by-step explanation:
1+3=4, 3+4=7, 7+11=18, so 18+11 = 29
I NEED HELP, WHAT IS THE ANSWER !!!!!!!!!!

Answers
Step-by-step explanation:
Hey there!
From the given figure;
Measure of angle V + measure of angle W = measure of angle VUF {exterior angle is equal to the sum of opposite interior angles}
Therefore, angle VUF= 94°.
Hope it helps!
Answer:
<V + <W = < VUF
94 = < VUF
Step-by-step explanation:
The exterior angle is equal to the sum of the opposite interior angles
<V + <W = < VUF
71+ 23 = < VUF
94 = < VUF
The price of a plain bowl plus the price
of
extra ingredients equals $

Answers
Answer:3,13
Step-by-step explanation:the price of the bowl is 10$ then you add 3 extra ingredients for a dollar each 10+3=13
Answer:
3,13
Step-by-step explanation:
use the power series 1 1 x = [infinity] (−1)nxn n = 0 , |x| < 1 to find a power series for the function, centered at 0. f(x) = ln(x4 1)
Answers
The power series representation for f(x) = ln(x^4 + 1), centered at 0, is:
f(x) = x^4 - x^8/2 + x^12/3 - x^16/4 + ..
To find a power series representation for the function f(x) = ln(x^4 + 1), we can start by using the logarithmic identity ln(1 + u) = u - (u^2)/2 + (u^3)/3 - (u^4)/4 + ..., valid for |u| < 1.
In this case, have u = x^4, so we can substitute it into the logarithmic identity:
ln(x^4 + 1) = x^4 - (x^4)^2/2 + (x^4)^3/3 - (x^4)^4/4 + ...
Simplifying the terms, we get:
ln(x^4 + 1) = x^4 - x^8/2 + x^12/3 - x^16/4 + ...
Now, we have expressed ln(x^4 + 1) as a power series centered at 0. The coefficients of the series are the coefficients of the powers of x^4: 1, -1/2, 1/3, -1/4, and so on.
Therefore, the power series representation for f(x) = ln(x^4 + 1), centered at 0, is:
f(x) = x^4 - x^8/2 + x^12/3 - x^16/4 + ...
Learn more about power series here:
https://brainly.com/question/29896893
#SPJ11
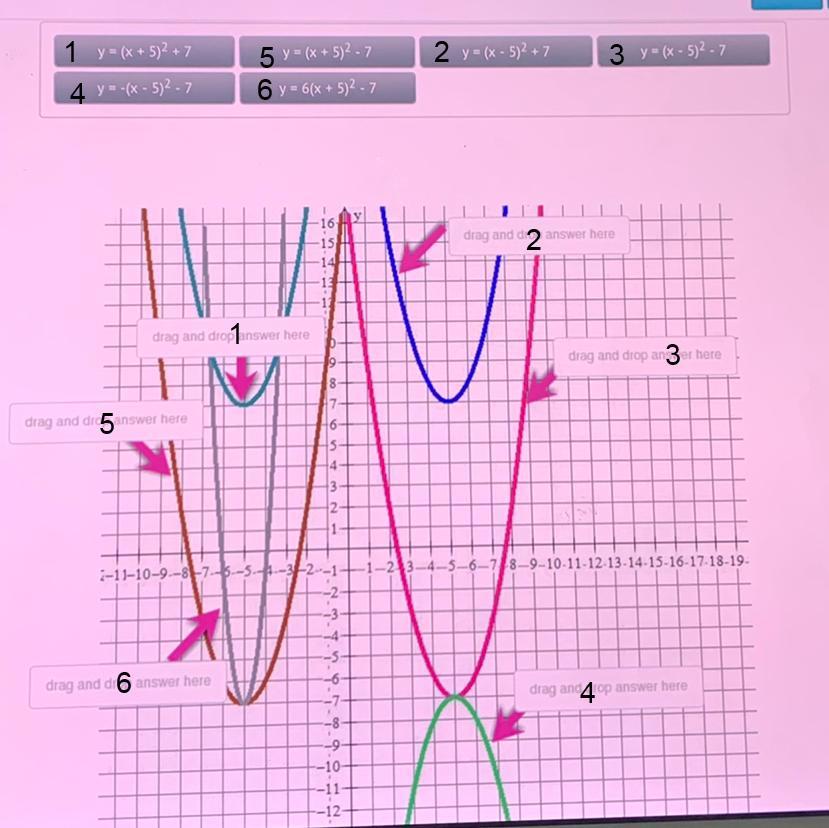
in the some important for of the image below about , some have more details available when you click on them Drag and drop each corresponding area it identities in the image

Answers
Vertex Form of a quadratic equation
A quadratic equation has the vertex form:
\(y=a(x-h)^2+k\)Where (h,k) is the vertex of the parabola and a is the leading coefficient.
If a is positive, the parabola is concave up, if a is negative, the parabola is concave down.
We'll identify each graph with a number so we can relate them with their corresponding equation.
Graph 1. Has the vertex at (-5,7) and opens up. The equation of this parabola (for a=1) is:
\(y=(x+5)^2+7\)Graph 2 has the vertex at (5,7) and opens up. The equation is:
\(y=(x-5)^2+7\)Graph 3 has the vertex at (5,-7) and opens up. The equation is
\(y=(x-5)^2-7\)Graph 4 has the vertex at (5,-7) and opens down. The equation is
\(y=-(x-5)^2-7\)Graph 5 has the vertex at (-5,-7) and opens up. The equation is
\(y=(x+5)^2-7\)Finally, graph 6 has the same vertex as graph 5 and opens up also, but it grows much faster than that one. The difference is that the leading factor is greater than one. This corresponds to the equation
\(y=6(x+5)^2-7\)The image below shows the correspondence between the graphs and their equations labeled with numbers.
you are dealt a hand of three cards, one at a time. find the probability that your cards are all face cards.
Answers
The probability that your cards are all face cards are,
The first club you get is the third card dealt P = 0.145Your cards are all black \(P_{all are black}\) = 0.116You get no hearts \(P_{no heart}\) = 0.413You have at least one red card \(P_{at least one red}\) = 0.884We know that Total number of cars is 52 .
26 red and 26 is black.
13 are hearts ,
13 are diamonds,
13 are clubs,
13 are spades.
(a) The first club you get is the third card dealt,
Probability P (first club get is the third card dealt) = P(Non-club x Non club x club)
So,
P = \(\frac{39}{52} * \frac{38}{51} * \frac{13}{50}\)
P = 0.145
(b) Your cards are all black,
\(P_{all are black}\) = \(\frac{26}{52} *\frac{25}{51} *\frac{24}{50}\)
\(P_{all are black}\) = 0.116
(c) You get no hearts,
\(P_{no heart}\) = \(\frac{39}{52} *\frac{38}{51} *\frac{37}{50}\)
\(P_{no heart}\) = 0.413
(d) You have at least one red card,
\(P_{at least one red}\) = 1 - \(P_{no red}\)
\(P_{no red}\) = \(\frac{26}{52} *\frac{25}{51} *\frac{24}{50}\)
\(P_{no red}\) = 0.116
\(P_{at least one red}\) = 1 - 0.116
\(P_{at least one red}\) = 0.884
Therefore,
The probability that your cards are all face cards are,
The first club you get is the third card dealt P = 0.145Your cards are all black \(P_{all are black}\) = 0.116You get no hearts \(P_{no heart}\) = 0.413You have at least one red card \(P_{at least one red}\) = 0.884To learn more about Probability visit :
brainly.com/question/12995031
#SPJ4
(PLEASE HELP, ONLY ANSWER IF YOU KNOW) what is the surface area of this design 10in 10in 5 in 5in 8in 2in

Answers
Answer:
C. 440 in²Step-by-step explanation:
Area of top and bottom faces:
2(10*10) = 200 in²Area of front and back faces:
2(10*10 - 8*5) = 2(100 - 40) = 2(60) = 120 in²Area of left and right faces:
2(10*10 - 8*5) = 2(100 - 40) = 2(60) = 120 in²Total surface area:
S = 200 + 120*2 = 440 in²Correct choice is C
Answer the following. a) Find h b) Find x

Answers
Answer:
a) h = 15
b) x = 4
Step-by-step explanation:
a) set up a proportion:
5 = h
8 24
cross-multiply:
8h = 120
h = 15
b) x + 5 = x + 5 + 15
5x + 1 5x + 1 + 35
cross-multiply:
(x + 5)(5x + 36) = (5x + 1)(x + 20)
5\(x^{2}\) + 61x + 180 = 5\(x^{2}\) + 101x + 20
180 = 40x + 20
160 = 40x
x = 4
a uniformly charged thin rod lies along the x axis from x = 0 to x = +[infinity].
Answers
In this scenario, we have a uniformly charged thin rod extending along the x-axis from the origin (x = 0) to positive infinity (x = +∞).
The term "uniformly charged" means that the charge is distributed evenly throughout the entire length of the rod.
To analyze this situation, we can consider the following steps: 1. Determine the linear charge density (λ) of the rod. Since the rod is uniformly charged, λ remains constant along its entire length. λ is usually given in units of charge per length (e.g., coulombs per meter).
2. To find the electric field at a particular point along or outside the rod, we can break the rod into infinitesimally small segments (dx) and consider the contribution of the electric field (dE) from each of these segments.
3. Calculate the electric field (dE) produced by each segment at the desired point using Coulomb's equations , considering the linear charge density (λ) and distance between the segment and the point.
4. Integrate the electric field contributions (dE) from all segments along the entire length of the rod (from x = 0 to x = +∞) to find the total electric field (E) at the point of interest.
By following these steps, you can analyze the electric field and related properties of a uniformly charged thin rod extending along the x-axis from x = 0 to x = +∞.
To know more about equation click here
brainly.com/question/649785
#SPJ11