Find the functional value.
f(0) if f(x) = x - 3x^2
Answers
Answer:
I hate to break it to you but it's 0.
Related Questions
what's the z-score for the lowest FinalGrade for Freshman

Answers
The z-score for the lowest final grade for a freshmen is given as follows:
Z = -1.83.
How to calculate the z-score?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The parameters for this problem are given as follows:
\(\mu = 74.38, \sigma = 4.445, X = 66.25\)
Hence the z-score for the lowest final grade for a freshmen is obtained as follows:
Z = (66.25 - 74.38)/4.445
Z = -1.83.
More can be learned about z-scores at https://brainly.com/question/25800303
#SPJ1
If the temperature in Texas dropped 35 degrees in 7 hours on Tuesday. What is the change over time?
Answers
Answer:
5 degrees every hour.
Step-by-step explanation:
35/7=5
Answer: 5
Step-by-step explanation:
35 degrees / 7 hours = 5 degrees per hour
What exactly is the rule of this? (in words)
7.5 x 1000 = 7500
5.9 x 10 = 59
9.4 x 100 = 940
8.3 / 1000 = 0.0083
6.5 / 10 = 0.65
6.6 / 100 = 0.066
/ means divided by
x means multiply
Answers
Answer:
the rule is scientific notation. if you are multiplying, move the decimal point over the amount of zeros to the right. if dividing, move the decimal point over to the left for the number of zeros there are.
Step-by-step explanation:
In △JKL , if m∠ J < 90° , then ∠K and ∠L are _____
Answers
Both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
In triangle JKL, if angle J is less than 90 degrees, then angle K and angle L are both acute angles.
An acute angle is defined as an angle that measures less than 90 degrees. Since angle J is given to be less than 90 degrees, it is an acute angle.
In a triangle, the sum of the interior angles is always 180 degrees. Therefore, if angle J is less than 90 degrees, the sum of angles K and L must be greater than 90 degrees in order to satisfy the condition that the angles of a triangle add up to 180 degrees.
Hence, both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
For more questions on triangle
https://brainly.com/question/1058720
#SPJ8
the value of x in the solution to the system x+y=10 and x-y=4
Answers
Answer:
x = 7; y = 3
Step-by-step explanation:
I used the Trial and Error Method and found that x = 7 and y = 3
=> 7 + 3 = 10
=> 10 = 10. ✔
=> 7 - 3 = 4
=> 4 = 4. ✔
Therefore, x = 7 and y = 3
Hoped this helped.
What is the common difference in the arithmetic sequence 30, 27, 24, 21, 18, ...? a. -1 c. 3 b. -3 d. 30 Please select the best answer from the choices provided
Answers
Answer:
b. -3
Step-by-step explanation:
30 - 3 = 27
27 - 3 = 24
24 - 3 = 21....
The gross weekly sales at a certain super market are a Gaussian random with mean $2200 and standard deviation $230. Assume that the sales from week to week are independent.
A) Find the probability that the gross sales over the next two weeks exceed $5000.
B) Find the probability that the gross weekly sales exceed $2000 in at least 2 of the next 3 weeks.
Answers
Answer:
A) P(Z > 5000) = 0.0322
B) P( Y = 2 or 3) ≅ 0.9032
Step-by-step explanation:
From the given information;
Suppose the sales for the first week are denoted by X and the sales for the second week are denoted by Y.
Then;
X & Y are independent and they follow a normal distribution.
i.e.
\(XY \sim N(\mu,\sigma^2)\)
\(XY \sim N(2200,230^2)\)
If we set Z to be equal to X+Y
Then, \(Z \sim N(2 \times 2200,2 \times 230^2)\) since two normal distribution appears normal
\(Z \sim N(4400,105800)\)
So;
\(P(Z > 5000) = 1 - P( Z< \dfrac{x = \mu}{\sqrt{\sigma}})\)
\(P(Z > 5000) = 1 - P( Z< \dfrac{5000-4400}{\sqrt{105800}})\)
\(P(Z > 5000) = 1 - P( Z< \dfrac{600}{325.2691})\)
\(P(Z > 5000) = 1 - P( Z< 1.844626495)\)
\(P(Z > 5000) = 1 - P( Z< 1.85)\)
From the Z - tables;
P(Z > 5000) = 1 - 0.9678
P(Z > 5000) = 0.0322
B)
Let Y be the random variable that obeys the Binomial distribution.
Y represents the numbers of weeks in the next 3 weeks where the gross weekly sales exceed $2000
Thus;
\(Y \sim Bin(3,p)\)
where;
\(p = 1 - P( Z < \dfrac{2000-2200}{230})\)
\(p = 1 - P( Z < \dfrac{-200}{230})\)
p = 1 - P( Z < - 0.869565)
From the Z - tables;
p = 1 - 0.1924
p = 0.8076
Now;
P(Y ≥ 2) = P(Y = 2) + P( Y =3 )
Using the formula
\(P(X = r ) = ^nC_r \times p^r \times q ^{n-r}\)
\(P( Y = 2 \ or \ 3) =^ 3C_2 \times 0.8076^2 \times ( 1- 0.8076) ^ {3-2} + ^ 3C_3 \times 0.8076^3 \times ( 1- 0.8076) ^ {3-3}\)
\(P( Y = 2 \ or \ 3) =\dfrac{3!}{2!(3-2)!} \times 0.8076^2 \times ( 0.1924) ^ 1 + \dfrac{3!}{3!(3-3)!}\times 0.8076^3 \times ( 0.1924) ^ {0}\)
\(P( Y = 2 \ or \ 3) =0.3764600911 +0.526731063\)
P( Y = 2 or 3) = 0.9031911541
P( Y = 2 or 3) ≅ 0.9032
Solve the system of linear equations using substitution. Use a pencil and paper. Which expression would be easier to substitute into the other equation, in order to solve this problem? Explain your reasoning.
x=4y-9
x+4y=3
Answers
Answer:
(- 3, 1.5)
--------------------------
Given system:
x = 4y - 9x + 4y = 3The first expression is ready to be substituted as no further operation is required to simplify it.
4y - 9 + 4y = 38y - 9 = 38y = 12y = 12/8y = 1.5Find x:
x = 4*1.5 - 9x = 6 - 9x = - 3tanx(1+cos2x)=sin2x prove the identity
Answers
Using double angle identity, we are able to prove tan(x)(1 + cos(2x)) = sin(2x).
What is the prove of the given identity?To prove the identity tan(x)(1 + cos(2x)) = sin(2x), we can start by using trigonometric identities to simplify both sides of the equation.
Starting with the left-hand side (LHS):
tan(x)(1 + cos(2x))
We know that tan(x) = sin(x) / cos(x) and that cos(2x) = cos²(x) - sin²(x). Substituting these values, we get:
LHS = (sin(x) / cos(x))(1 + cos²(x) - sin²(x))
Next, we can simplify the expression by expanding and combining like terms:
LHS = sin(x) / cos(x) + sin(x)cos²(x) / cos(x) - sin³(x) / cos(x)
Simplifying further:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
Now, let's work on the right-hand side (RHS):
sin(2x)
Using the double angle identity for sine, sin(2x) = 2sin(x)cos(x).
Now, let's compare the LHS and RHS expressions:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
RHS = 2sin(x)cos(x)
To prove the identity, we need to show that the LHS expression is equal to the RHS expression. We can combine the terms on the LHS to get a common denominator:
LHS = [sin(x) - sin³(x) + sin(x)cos²(x)] / cos(x)
Now, using the identity sin²(x) = 1 - cos²(x), we can rewrite the numerator:
LHS = [sin(x) - sin³(x) + sin(x)(1 - sin²(x))] / cos(x)
= [sin(x) - sin³(x) + sin(x) - sin³(x)] / cos(x)
= 2sin(x) - 2sin³(x) / cos(x)
Now, using the identity 2sin(x) = sin(2x), we can simplify further:
LHS = sin(2x) - 2sin³(x) / cos(x)
Comparing this with the RHS expression, we see that LHS = RHS, proving the identity.
Learn more on trigonometric identity here;
https://brainly.com/question/24496175
#SPJ1
This is a question I need help with

Answers
Answer:
55
Step-by-step explanation:
180=35+90+m∠3
Ok Billy needs 90 lbs of garden soil to landscape a building. In the company storage area, he finds 2 cases holding 24 3/4 soil each, and a third case holding 19 3/8 lb. How much gardening does Bill still need in oder to do the job?
Answers
Answer:
1/3
Step-by-step explanation:
All of the points in the picture are on the same line,
(6, 10)
(0,8)
(4.b)
(2.2)
1. Find the slope of the line. One
swer only:

Answers
Answer:
m=2
Step-by-step explanation:
use points (2,2) and (6,10)
(find y of slope)10-2=8
(find x of slope)6-2=4
8/4=2
Rylon Corporation manufactures Brute and Chanelle perfumes. The raw materials needed to manufacture each type of perfume can be purchased for $3 per pound. Processing 1 lb of raw material requires 1 hour of laboratory time. Each pound of processed raw material yields 3 oz of Regular Brute Perfume and 4 oz of Chanelle perfume. Regular Brute can be sold for $7/oz and Regular Chanelle for $6/oz. Rylon also has the option of further processing Regular Brute and Regular Chanelle to produce Luxury Brute, sold at $18/oz, and Luxury Chanelle, sold at $14/oz. Each ounce of Regular Brute processed further requires an additional 3 hours of laboratory time and $4 processing cost and yields 1 oz of Luxury Brute. Each ounce of Regular Chanelle processed further requires an additional 2 hours of laboratory time and $4 processing cost and yields 1 oz of Luxury Chanelle. Each year, Rylon has 6,000 hours of laboratory time available and can purchase up to 4,000 lb of raw material. Question : what is the simplex algorithm (manual table ) to find a solution to the linear programming problem given above
Answers
Convert the problem to standard form and write the initial tableau with slack variables:
Maximize
\(Z = 7*3 + 6*4 + 18*5 + 14*6 - 3*1 - 3*2 - 4*5 - 4*6\)
Subject to:
\(x1 + x2 + s1 = 4000\\x3 - (1/3)*1 + (1/3)*5 = 0\\x4 - (1/3)*2 + (1/2)*6 = 0\\x3*1 + 3*2 + 3*3 + 3*4 + 3*5 + 2*6 + s2 = 6000\)
All variables are non-negative.
Tableau
x1 x2 x3 x4 x5 x6 s1 s2 b
Z -3 -3 7 6 18 14 0 0 0
s1 1 1 0 0 0 0 1 0 4000
s2 3 3 3 3 3 2 0 1 6000
x5 0 0 1 0 1/3 0 0 0 0
x6 0 0 0 1 0 1/2 0 0 0
The basic variables are s1, s2, x5, and x6.
Step 1: Choose entering variable. The most positive coefficient in objective row is 18, corresponding to x5. x5 enters the basis.
Step 2: Choose the leaving variable. The minimum ratio of right-hand side to coefficient of x5 is 12000/(1/3) = 36000,
corresponding to s1. s1 leaves the basis.
Step 3: Perform, pivot operation to make x5 the basic variable for s1. Divide, pivot row by 1/3 and subtract appropriate multiples of the pivot row from other rows to make other entries in column 5 zero.
x1 x2 x3 x4 x5 x6 s1 s2 b
Z -3 -3 7 6 18 14 0 0 0
x5 0 0 1 0 1/3 0 0 0 0
s2 3 3 3 3 2 2/3 2/3 0 1/3 24000
x3 1 0 1/3 0 1/3 0 -1/3 0 0
x4 0 1 0 1/3 0 1/2 -1/6 0 0
The basic variables are x5, x3, x4, and s2.
Step 4: Choose the entering variable. The most positive coefficient in the objective row is 7, corresponding to x3. x3 enters the basis.
Step 5: Determine the leaving variable. The right-hand side's minimum ratio to the coefficient of x3 is 0, indicating that x3 can be increased without bound. This implies that the optimal solution is unbounded and that there is no finite optimal value for the problem.
As a result, the simplex algorithm demonstrates that the given linear programming problem lacks a feasible solution. This means that it is not possible to meet all of the constraints at the same time.
For more question on simplex algorithm click on
https://brainly.com/question/29554333
#SPJ4
Simplify (6x ^ 2 + 11x - 3) + (2x ^ 2 - 17x - 4) . (1 point)
1 ) 8x ^ 2 + 6x - 1
2) 8x ^ 2 - 6x - 7
3 ) 8x ^ 2 + 6x + 1
4 ) 8x ^ 2 - 6x + 7
Answers
Answer:
2) 8x^2 -6x-7 hope this helps
A previous survey of Washington residents showed that 18% of residents accessed a state park within the last 12 months. This year, the state would like to re-administer the survey, but wants to be sure the Margin of Error in their new study will be at most 4%. Assuming they believe the previous survey's results were reliable, how many samples should they take to ensure their Margin of Error is at most 4% if they plan to analyze the data using a 95% confidence interval
Answers
Using the z-distribution for the margin of error, it is found that 355 samples should be taken.
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which z is the z-score that has a p-value of \(\frac{1+\alpha}{2}\).
The margin of error is given by:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
The estimate is of 18%, hence \(\pi = 0.18\).
95% confidence, hence \(\alpha = 0.95\), z is the value of Z that has a p-value of \(\frac{1+0.95}{2} = 0.975\), so \(z = 1.96\).
The minimum sample size is n for which M = 0.04, hence:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
\(0.04 = 1.96\sqrt{\frac{0.18(0.82)}{n}}\)
\(0.04\sqrt{n} = 1.96\sqrt{0.18(0.82)}\)
\(\sqrt{n} = \frac{1.96\sqrt{0.18(0.82)}}{0.04}\)
\((\sqrt{n})^2 = \left(\frac{1.96\sqrt{0.18(0.82)}}{0.04}\right)^2\)
\(n = 354.4\)
Rounding up, 355 samples should be taken.
A similar problem is given at https://brainly.com/question/14936818
I am a multiple of 2 , 5 and 7. The sum of my three digits is 10 . I am not 280.
Answers
The multiple of 2, 5, and 7, such that the sum of the 3 digits is 10 is:
630
How to find the number?We want to find a number that is a multiple of 2, 5 and 7, such that the sum of the 3 digits is 10. (such that the number is not 280)
So our number N is of the form:
N = a*(2*5*7)
Where a is an integer.
N = a*70
Here we just need to find the value of a such that the sum of the 3 digits of the outcome is equal to 10.
For example, if a = 2 then:
N = 2*70 = 140
The sum gives 1 + 4 + 0 = 5
Now we jut need to keep trying values of a.
Eventually, we will get to:
if a = 9 then:
N = 9*70 = 630
The sum gives: 6 + 3 + 0 = 10
So this is our number.
Learn more about multiples:
https://brainly.com/question/251701
#SPJ1
Hannah owes $20 to her mom. Then, she borrows $15 more from her mom. What is Hannah's "balance'' now?
Answers
Answer:
-$35.00
Step-by-step explanation: I think
In a study of the effect of college student employment on academic performance, the following summary statistics for GPA were reported for a sample of students who worked and for a sample of students who did not work. The samples were selected at random from working and nonworking students at a university. (Use a statistical computer package to calculate the P-value. Use μemployed − μnot employed. Round your test statistic to two decimal places, your df down to the nearest whole number, and your P-value to three decimal places.)
Sample Size Mean GPA Standard Deviation
Students Who
Are Employed 172 3.22 0.475
Students Who
Are Not Employed 116 3.33 0.524
t =
df =
P =
Does this information support the hypothesis that for students at this university, those who are not employed have a higher mean GPA than those who are employed? Use a significance level of 0.05.
Answers
Answer:
Step-by-step explanation:
This is a test of 2 independent groups. The population standard deviations are not known. Let μemployed(μ1) be the sample mean of students who are employed and μnot employed(μ2) be the sample mean of students who are not employed
The random variable is μ1 - μ2 = difference in the mean of the employed and unemployed students.
We would set up the hypothesis.
The null hypothesis is
H0 : μ1 = μ2 H0 : μ1 - μ2 = 0
The alternative hypothesis is
H1 : μ1 < μ2 H1 : μ1 - μ2 < 0
Since sample standard deviation is known, we would determine the test statistic by using the t test. The formula is
(μ1 - μ2)/√(s1²/n1 + s2²/n2)
From the information given,
μ1 = 3.22
μ2 = 3.33
s1 = 0.475
s2 = 0.524
n1 = 172
n2 = 116
t = (3.22 - 3.33)/√(0.475²/172 + 0.524²/116)
t = - 1.81
The formula for determining the degree of freedom is
df = [s1²/n1 + s2²/n2]²/(1/n1 - 1)(s1²/n1)² + (1/n2 - 1)(s2²/n2)²
df = [0.475²/172 + 0.524²/116]²/[(1/172 - 1)(0.475²/172)² + (1/116 - 1)(0.524²/116)²] = 0.00001353363/0.00000005878
df = 230
We would determine the probability value from the t test calculator. It becomes
p value = 0.036
Since alpha, 0.05 > than the p value, 0.036, then we would reject the null hypothesis.
Therefore, at a 5% significant level, this information support the hypothesis that for students at this university, those who are not employed have a higher mean GPA than those who are employed
A college basketball player makes 80% of his freethrows. Over the course of the season he will attempt 100 freethrows. Assuming free throw attempts are independent, the probability that the number of free throws he makes exceeds 80 is approximately:____________.
A) 0.2000
B) 0.2266
C) 0.5000
D) 0.7734
Answers
Answer:
The probability that the number of free throws he makes exceeds 80 is approximately 0.50
Step-by-step explanation:
According to the given data we have the following:
P(Make a Throw) = 0.80%
n=100
Binomial distribution:
mean: np = 0.80*100= 80
hence, standard deviation=√np(1-p)=√80*0.20=4
Therefore, to calculate the probability that the number of free throws he makes exceeds 80 we would have to make the following calculation:
P(X>80)= 1- P(X<80)
You could calculate this value via a normal distributionapproximation:
P(Z<(80-80)/4)=1-P(Z<0)=1-50=0.50
The probability that the number of free throws he makes exceeds 80 is approximately 0.50
The probability that the number of free throws he makes exceeds 80 is approximately 0.5000.
Given that,
A college basketball player makes 80% of his free throws.
Over the course of the season, he will attempt 100 free throws.
Assuming free throw attempts are independent.
We have to determine,
The probability that the number of free throws he makes exceeds 80 is.
According to the question,
P(Make a Throw) = 80% = 0.80
number of free throws n = 100
Binomial distribution:
Mean: \(n \times p = 0.80 \times 100 = 80\)
Then, The standard deviation is determined by using the formula;
\(= \sqrt{np(1-p)} \\\\=\sqrt{80\times (1-0.80)}\\\\= \sqrt{80 \times 0.20 } \\\\= \sqrt{16} \\\\= 4\)
Therefore,
To calculate the probability that the number of free throws he makes exceeds 80 we would have to make the following calculation:
\(P(X>80)= 1- P(X<80)\)
To calculate this value via a normal distribution approximation:
\(P(Z<\dfrac{80-80}{4})=1-P(Z<0)=1-0.50=0.5000\)
Hence, The probability that the number of free throws he makes exceeds 80 is approximately 0.5000.
To know more about Probability click the link given below.
https://brainly.com/question/21586810
Consider two boxes, one containing 3 blue and 2 red marbles, the other contains 3 blue and 5 red marbles. A box is selected at random (i.e. 50:50 chance of selecting either box), and a marble is drawn from it at random. Part a) What is the probability that the selected marble is blue? Do NOT round your answer. Create a variable pB that stores the value of this probability. That is, write your answer as
pb =
Answers
Probability of getting a marble is 0.3.
Probability is a branch of math which deals with finding out the likelihood of the occurrence of an event. measures the chance of an event happening and is equal to the number of favorable events divided by the total number of events. The value of probability ranges between 0 and 1, where 0 denotes uncertainty and 1 denotes certainty.
Two boxes Probability of selecting either of the box = 0.5
Box A contains: 3 blue and 2 red marbles. So, probability of selecting blue marbles,
let p(B1) = [3C1/5C1 ]= 0.6*0.5 = 0.3 (As Probability of selecting box 1 is 50:50 )
Box contains : 3 blue and 5 red marbles,
let p(B2) = [3C2/5C2] = 0.6*0.5 = 0.3 ( As the probability of selecting box 2 is also 50:50 )
So, the final probability of getting a blue ball is 0.3.
To learn more about probability :
https://brainly.com/question/30356024
#SPJ4
Probability of getting a marble is 0.3.
Probability is a branch of math which deals with finding out the likelihood of the occurrence of an event. measures the chance of an event happening and is equal to the number of favorable events divided by the total number of events. The value of probability ranges between 0 and 1, where 0 denotes uncertainty and 1 denotes certainty.
Two boxes Probability of selecting either of the box = 0.5
Box A contains: 3 blue and 2 red marbles. So, probability of selecting blue marbles,
let p(B1) = [3C1/5C1 ]= 0.6*0.5 = 0.3 (As Probability of selecting box 1 is 50:50 )
Box contains : 3 blue and 5 red marbles,
let p(B2) = [3C2/5C2] = 0.6*0.5 = 0.3 ( As the probability of selecting box 2 is also 50:50 )
So, the final probability of getting a blue ball is 0.3.
To learn more about probability :
brainly.com/question/29381779
#SPJ4
The points A, B and C have position vectors a, b, c, referred to an origin O. i. Given that the point X lies on AB produced so that AB : BX = 2 : 1, find x, the position vector of X, in terms of a and b. ii. If Y lies on BC, between B and C so that BY : Y C = 1 : 3, find y, the position vector of Y, in terms of a and b iii. Given that Z is the midpoint of AC, Calculate the ratio XY : Y Z.
Answers
i. The position vector of X is 2b - a.
ii. The position vector of Y is (3b + c)/4.
iii. The ratio XY : Y Z is \(|(2b - a) - ((3b + c)/4)|/|((3b + c)/4) - (a + c)/2|\). Simplifying this expression will give us the final ratio.
i. To find the position vector x of point X, we can use the concept of vector addition. Since AB : BX = 2 : 1, we can express AB as a vector from A to B, which is given by (b - a). To find BX, we can use the fact that BX is twice as long as AB, so BX = 2 * (b - a). Adding this to the vector AB will give us the position vector of X: x = a + 2 * (b - a) = 2b - a.
ii. Similar to the previous part, we can express BC as a vector from B to C, which is given by (c - b). Since BY : YC = 1 : 3, we can find BY by dividing the vector BC into four equal parts and taking one part, so BY = (1/4) * (c - b). Adding this to the vector BY will give us the position vector of Y: y = b + (1/4) * (c - b) = (3b + c)/4.
iii. Z is the midpoint of AC, so we can find Z by taking the average of the vectors a and c: z = (a + c)/2. The ratio XY : YZ can be calculated by finding the lengths of the vectors XY and YZ and taking their ratio. Since XY = |x - y| and YZ = |y - z|, we have XY : YZ = |x - y|/|y - z|. Plugging in the values of x, y, and z we found earlier, we get XY : YZ =\(|(2b - a) - ((3b + c)/4)|/|((3b + c)/4) - (a + c)/2|\).
For more such questions on vector
https://brainly.com/question/15519257
#SPJ8
A factory packed 85 teddy bears into large boxes for delivery to a toy store. Each large box held 9 teddy bears. The remaining bears was packed into a small box. How many teddy bears were packed in the small box. what i am asking is what the remainder for this question.
Answers
Answer:
9.4
Step-by-step explanation:
85/9=9.4...
I put ... at end because it continues forever the 4s I hoped I helped
If 6 is an element in the domain of f(x) = (8x-16)/2, what is the corresponding element in the range?
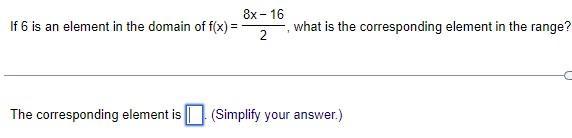
Answers
If 6 is an element in the domain of f(x) = (8x - 16)/2, the corresponding element in the range include the following: [16].
What is a domain?In Mathematics, a domain is the set of all real numbers for which a particular function is defined.
What is a range?In Mathematics, a range can be defined as the set of all real numbers that connects with the elements of a domain.
Based on the information provided, we have the following function rule:
Function, f(x) = y = (8x - 16)/2
When the domain x = 6, the range (y) of this function is given by;
Range, y = (8(6) - 16)/2
Range, y = (48 - 16)/2
Range, y = 32/2
Range, y = 16.
Read more on range here: https://brainly.com/question/16678516
#SPJ1
16
Find the exact value of x
X =
30
Do the side lengths form a Pythagorean triple?
O Yes
O No
Answers
The exact value of x is √1156 and it follows the Pythagorean triple
Finding the exact value of xFrom the question, we have the following parameters that can be used in our computation:
Legs of the right triangle = 16 and 30
Using the pythagoras theorem, we have
Hypotenuse^2 = the sum of the squares of the other lengths
So, we have
x^2 = 16^2 + 30^2
When evaluated, we have
x^2 = 1156
This gives
x = √1156
Hence, the exact value is √1156
Read more about pythagoras theorem at
https://brainly.com/question/231802
#SPJ1
Convert: 112 meters = ______ centimeters
11,200 cm
1,120 cm
1.12 cm
112,000 cm
Answers
Answer:
11,200
Step-by-step explanation:
You can look up "Meters to Centimeters" and that should help you in the future
Answer:
11,200
Step-by-step explanation:
Use the unit circle to evaluate the followingHow do I solve this ?

Answers
So we want to evaluate:
\(\tan (\frac{2\pi}{3})\)For this, we might convert 2pi/3 to degrees.
This, is to make the graph more understandable.
Remember that:
\(\pi=180\)So we could make the following ratio:
\(\begin{gathered} \pi=180 \\ \frac{2\pi}{3}=x \end{gathered}\)Solving for x:
\(\begin{gathered} x=\frac{\frac{2\pi}{3}\cdot180}{\pi} \\ \\ x=\frac{120\pi}{\pi}=120 \end{gathered}\)Therefore, x=120°. Now, we could graph:
So,
\(\tan (120)=\frac{\sin120}{\cos120}=\frac{\sin 60}{-\cos 60}=\frac{\frac{\sqrt[]{3}}{2}}{-\frac{1}{2}}=-\sqrt[]{3}\)
Suppose Allan is going to build a playlist that contains 14 songs. In how many ways can Allan arrange the 14 songs on the playlist?
Allan can arrange the 14 songs on the playlist in
different ways.
Answers
Answer:
Step-by-step explanation:
14!=8.71782912x10^10
14!=14x13x12x11x10x9x8x7x6x5x4x3x2x1
Hello, I was wondering if you could help me with this question: Step 8 - simplify

Answers
In this prooof, we need to complete the 8th step to simplify the expression.
We are given:
\((1+d^2)+(e^2+1)=d^2-2de+e^2\)Combining like terms on the left-hand side, we get
\(2+d^2+e^2=d^2-2de+e^2\)Subtracting the d squared term from each side, we have:
\(2+e^2=-2de+e^2\)Next, we subtract the e squared term from each side:
\(2=-2de\)Finally, we divide by -2 on each side:
\(-1=de\)Since d represents the slope of line AB and e represents the lope of line BC, we show that the slopes multiplied together give us -1.
During a review game, Mr. Pai's class correctly answered 65 questions on the first try. If there were 75 questions in the game, at what rate were questions answered correctly on the first try? Express your answer as a decimal. Round to the nearest thousandth.
A. 0.087
B. 0.867
C. 0.133
D. 1.154

Answers
Using the concept of ratio, the rate at which questions were answered correctly is 0.867 which is option B
What is RateRate can be defined as comparing two or more ratio with a standard value.
The rate of correct answer can be calculated using the ratio between the number of correct answers to numbers of questions answered.
The rate is given as;
rate = 65 / 75
rate = 0.867
The rate of correct answers is 0.867
Learn more on rates here;
https://brainly.com/question/843074
#SPJ1
If a ^-1/2 = x, where a > 0, what is a in terms of x?
a. √x
b. -√x
c. 1/x^2
d. -1/x^2
Answers
9514 1404 393
Answer:
c. 1/x^2
Step-by-step explanation:
You want to solve for a:
1/√a = x
1/a = x^2 . . . . . square both sides
1/x^2 = a . . . . . multiply both sides by a/x^2
Answer:
14743
Step-by-step explanation:
B. the business world and its industries control those in poverty
C. that the place is polluted and depressing