Find the function f given that the slope of the tangent line at any point (x, f(x)) is f '(x) and that the graph of f passes through the given point.f '(x) = 4(2x − 9)^3 (5, 11/2)
Answers
Answer:
\(f(x)=\frac{1}{2}(2x-9)^4+5\)Explanation:
Given f'(x) defined below:
\(f^{\prime}(x)=4(2x-9)^3_{}\)First, integrate f'(x) to find f(x).
\(\int f^{\prime}(x)=\int 4(2x-9)^3dx=4\int (2x-9)^3dx\)Let u = 2x-9
\(u=2x-9\implies du=2dx\implies dx=\frac{du}{2}\)Thus:
\(\begin{gathered} f(u)=4\int u^3\frac{du}{2}=\frac{4}{2}\int u^3du=\frac{2u^4}{4}=\frac{1}{2}u^4+C \\ \implies f(u)=\frac{1}{2}u^4+C \end{gathered}\)Replace u=2x-9.
\(f(x)=\frac{1}{2}(2x-9)^4+C\)Next, using the point (5,11/2), we find the value of C, the constant of integration.
At (5, 11/2)
\(\begin{gathered} x=5,f(x)=\frac{11}{2} \\ f(x)=\frac{1}{2}(2x-9)^4+C \\ \frac{11}{2}=\frac{1}{2}(2\lbrack5\rbrack-9)^4+C \\ \frac{11}{2}=\frac{1}{2}(10-9)^4+C \\ \frac{11}{2}=\frac{1}{2}(1)^4+C \\ \frac{11}{2}=\frac{1}{2}+C \\ C=\frac{11}{2}-\frac{1}{2}=\frac{10}{2}=5 \end{gathered}\)Therefore, the function f(x) is:
\(f(x)=\frac{1}{2}(2x-9)^4+5\)Related Questions
pls help!!!!!!!!!!!1
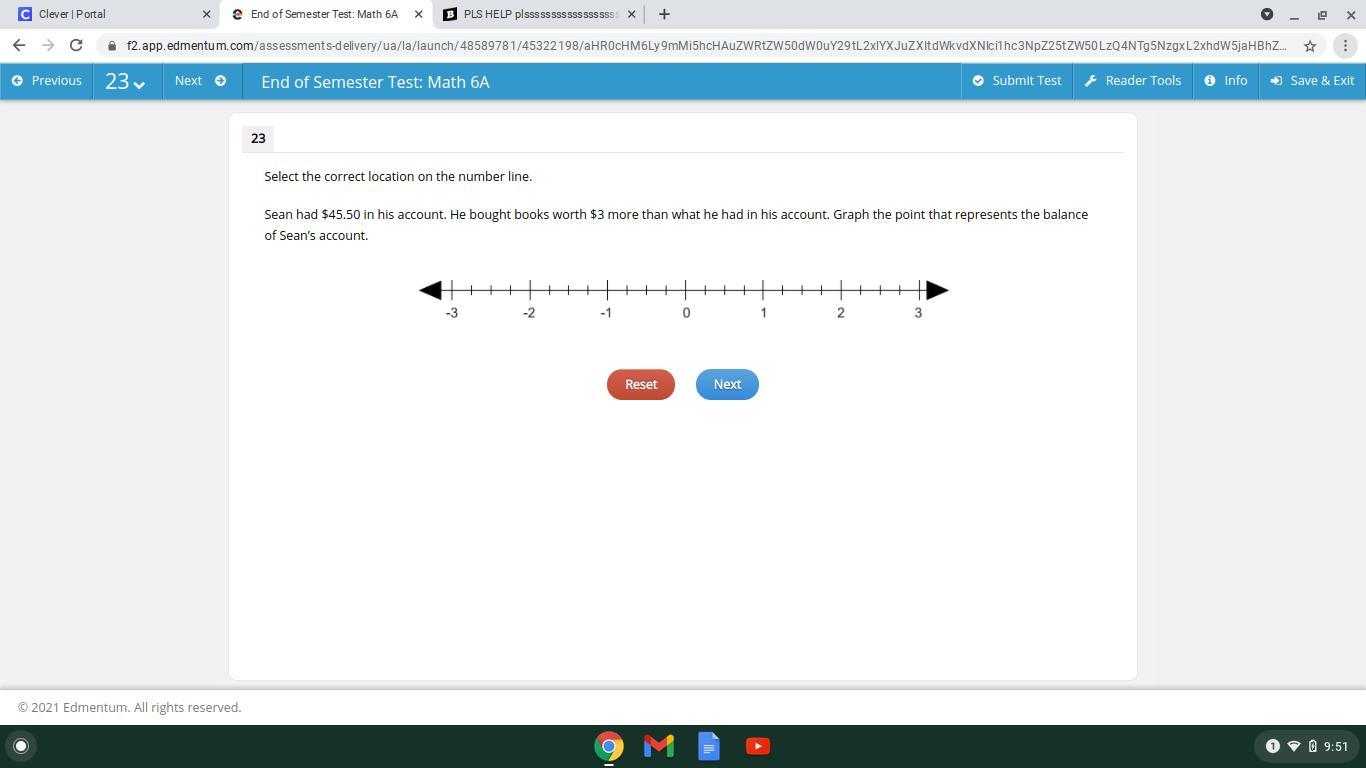
Answers
Answer:lol it's -3
Step-by-step explanation: it's 3 because you had dirt 45.50 in your account and then you have to get books and those books will cost $3 more which means that you don't have that money since it indicates that in the problem which means that it would be -3 because you don't have the money so that's why I think it's negative 3.
Sarah's fish tank holds 32 litters of water. Sarah uses a 4 liter container to fill the tank. how many times will Sarah need to fill the 4 liter container in order to fill the fish tank.
Answers
Answer:
8 times,
Step-by-step explanation:
4 x 8 is 32
We need help with this math problem so we can be done for today
Answers
Given:
Initial amount is : $75.
Deposits amount every month is: $25
Total amount is after m months
\(=75+25m\)after m month account balance is $(75+25m).
help with this please

Answers
Step-by-step explanation:
I cannot do this table nicely here, but it is totally simple : the first number in brackets is the input, the second number the corresponding output.
you can do this easily and faster than in here.
it is not a function, because e.g. the input values -2 and 4 have more than 1 output value assigned (in different offered pairs, sure, but the whole group of ordered pairs defines the relationship).
-2 has 6 and 8
4 has 6 and 15
to be a function, each input value can have only one associated output value.
How do you do letter b?

Answers
Answer: 175
Step-by-step explanation:
\(g(35)= \int\limits^{35}_0 {f(x)} \, dx =\int\limits^{30}_0 {f(x)} \, dx +\int\limits^{35}_{30} {f(x)} \, dx\)
= 137.5 + 37.5
= 175
Answer:
g(35) = 137.5
Step-by-step explanation:
g(35) = g(30) + [g(35) - g(30)]
g(35) = 100 + 5(15)/2
g(35) = 137.5
How many gallons of a 60% antifreeze solution must be mixed with 70 gallons of 20% antifreeze to get a misture that is 50% antifreeze? Use the she-step method
Answers
Answer:
210 gaL 60 % Antifreeze IIStep-by-step explanation:
In the problem, there are two types of antifreeze
antifreeze I and
antifreeze II
antifreeeze I 20 ----70 gal
Antifreeze II 60 ----- x gal
Total 50 ---------------- (70 + x ) gal
20*70+60*x=50(70+x)
1400+60x=3500+50x
60x-50x=3500-1400
10x=2100
x= 210
x=210 gaL 60 % Antifreeze II
If (he)={(0,1),(2,3),(-4,1)}, find h^-1(x)
Answers
The given function is
\(h(x) = \{ (0,1), (2,3), (-4, 1) \}\)
The inverse function is
\(h^{-1}(x) = \{ (1,0), (3,2), (1,-4)\}\)
To get the inverse, we swap each x and y coordinate.
The rule is \((x,y) \to (y,x)\)
So that's why the point (0,1) becomes (1,0) for instance.
One by one, without spaces, Ivan wrote the numbers from 1 to 100. Which digit is in the 100th place?
Answers
What’s the lateral area of this

Answers
Answer:
240 in²
Step-by-step explanation:
You want the lateral area of a triangular prism with triangular base having sides 6 in, 8 in, and 10 in, and a distance between them of 10 in.
Lateral areaThe lateral area of a triangular prism is the area of the three rectangular faces. The width of those faces is the "height" of the prism, given as 10 in. The total length of those faces is the perimeter of the base:
6 in + 8 in + 10 in = 24 in
The lateral area is ...
A = LW = (24 in)(10 in) = 240 in²
<95141404393>
8. The loudness of a sound depends on_____. A. The width of the wave B. The brightness of the wave C. The length of a sound wave D. The wave height or amplitude
Answers
Answer:
D
Step-by-step explanation:
loudness depends on the amplitude or height of the sound waves
For each value of U determine whether it is a solution to 35>24+u

Answers
35 > 24 + u
If u = 10. 35 > 24 + 10, true
If u = 6. 35 > 24 + 6, true
If u = 14. 35 > 24 + 14, false
If u = 11. 35 > 24 + 11, false
1
4
(
8
−
6
x
+
12
)
?
1
4
(
8
−
6
x
+
12
)
?
A.
7
2
x
7
2
x
B.
−
13
2
x
−
13
2
x
C.
−
6
x
+
14
−
6
x
+
14
D.
−
3
2
x
+
5
Answers
The equivalent expression is 5 - 3x/2. Option D
What are algebraic expressions?Algebraic expressions are described as expressions that are made up of variables, their coefficients, factors and constants.
these algebraic expressions are also composed of mathematical operations. These operations includes;
BracketParenthesesSubtractionMultiplicationDivisionAdditionFrom the information given, we have that;
1/ 4(8 - 6x + 12)
expand the bracket, we have;
Add the like terms
1/4(20 - 6x)
now, multiply the values, we have;
20 - 6x/4
Divide by the denominator
5 - 3x/2
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1
The complete question:
Simply the expression:
1/ 4(8 - 6x + 12)
Prove all the relation of quadric polynomial.
Kindly need help!!!
Answers
\({\large{\textsf{\textbf{\underline{\underline{Solution :}}}}}}\)
Let \(\alpha\) and \(\beta\) be the two zeroes of P(x) = \(\sf {a}^{2} + bx + c\)
• A polynomial is always equal to it's factors, also the constant "k" is not equal to zero
\( \tt \sf {a}^{2} + bx + c = k(x - \alpha )(x - \beta )\)
• Using distributive property
\(\tt \sf {a}^{2} + bx + c = k \bigg( {x}^{2} - \beta x - \alpha x + \alpha \beta \bigg)\)
\(\tt \sf {a}^{2} + bx + c = k {x}^{2} -k (\beta x )- k(\alpha x )+k( \alpha \beta )\)
• Taking common
\(\tt \sf {a}^{2} + bx + c = k {x}^{2} -kx (\beta + \alpha)+k( \alpha \beta ) - - (1)\)
• Equating coefficients of like terms
\( \sf \: a = k - - (2)\)
\( \sf b = - k( \alpha + \beta ) - - (3)\)
\( \sf c = k \alpha \beta - - (4)\)
★ From 3
\( \sf b = - k( \alpha + \beta ) - - (3)\)
★ From 2 we have a = k so we have -
\( \sf b = - a( \alpha + \beta ) \)
\(\sf - \dfrac{b}{a} = ( \alpha + \beta ) \)
\(\sf \therefore \boxed {{ \red{( \alpha + \beta ) = - \dfrac{b}{a} } }}\)
• Sum of zeros = \(- \dfrac{b}{a}\)
★ From 4
\( \sf c = k \alpha \beta - - (4)\)
★ From 2 we have a = k so we have -
\( \sf c = a \: \alpha \: \beta\)
\(\sf \dfrac{c}{a} = \alpha \beta\)
\(\sf \therefore \boxed {{ \red{( \alpha \beta ) = \dfrac{c}{a} } }}\)
• Product of zeros = \( \dfrac{c}{a}\)
Also,
★ From 1
\(\tt \sf {a}^{2} + bx + c = k {x}^{2} -kx (\beta + \alpha)+k( \alpha \beta ) - - (1)\)
\(\tt \sf {a}^{2} + bx + c = k \bigg( {x}^{2} -x ( \alpha + \beta ) + ( \alpha \beta \bigg) \)
• Now just put S instead of sum of zeroes and P instead of product of zeroes
\( \tt \sf {a}^{2} + bx + c = k \bigg( {x}^{2} -x ( S ) + ( P \bigg) \)
\(\tt \sf{a}^{2} + bx + c = \boxed{ \red{ \sf \tt k \bigg( {x}^{2} - Sx + ( P \bigg ) }}\)
\(\rule{280pt}{2pt}\)
Find the volume of each composite figure to the nearest whole number.

Answers
The volume of the composite figure in this problem is given as follows:
76 ft³.
How to obtain the volume of a rectangular prism?The volume of a rectangular prism, with dimensions defined as length, width and height, is given by the multiplication of these three defined dimensions, according to the equation presented as follows:
Volume = length x width x height.
The figure in this problem is composed by two prisms, with dimensions given as follows:
2 ft, 6 ft and 3 ft.2 ft, 4 ft and 8 - 3 = 5 ft.Hence the volume is given as follows:
2 x 6 x 3 + 2 x 4 x 5 = 76 ft³.
A similar problem about the volume of rectangular prisms is presented at brainly.com/question/22070273
#SPJ1
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
Solve for x.
37°
8 cm
x = [?] cm
X
Round to the nearest hundredth.
X
![Solve for x.378 cmx = [?] cmXRound to the nearest hundredth.X](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/5r3s734YNpMZhrSKBRqrQYrII2vYUjgx.png)
Answers
The measure of side length x in the right triangle is approximately 6.03 cm.
What is the measure of side length x?The figure in the image is a right triangle having one of its interior angle at 90 degrees.
From the figure:
Angle θ = 37 degrees
Adjacent to angle θ = 8 cm
Opposite to angle θ = x
To solve for the missing side length x, we use the trigonometric ratio.
Note that: tangent = opposite / adjacent
Hence:
tan( θ ) = opposite / adjacent
Plug in the given values and solve for x:
tan( 37 ) = x / 8
x = tan( 37 ) × 8
x = 6.03 cm
Therefore, the value of x is 6.03 cm.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Z = { x:x is an integer, x ≥ - 3 and x ≤ + 3}
Answers
Answer:
If this is asking for the set:
Z = {-3, -2, -1, 0, 1, 2, 3}
Step-by-step explanation:
Z is the set of all integers and it appears that you are being asked for the values in the set Z that are within the range: -3 ≤x ≤ 3
Optimal Chapter-Flight Fare If exactly 212 people sign up for a charter flight, Leisure World Travel Agency charges $292/person. However, if
more than 212 people sign up for the flight (assume this is the case), then each fare is reduced by $1 for each additional person. Determine how
many passengers will result in a maximum revenue for the travel agency. Hint: Let x denote the number of passengers above 212. Show that the
revenue function R is given by R(x) = (212+x)(292-x).
passengers
What is the maximum revenue?
$
What would be the fare per passenger in this case?
dollars per passenger
Answers
Answer:
Dollars per passenger would be $252.
The maximum revenue is $63,404.
Step-by-step explanation:
Let's define the number of passengers above 212 as x.
The revenue function is given by R(x) = (212 + x)(292 - x).
We can expand and simplify the revenue function:
\(R(x) = 212 * 292 + 212 * (-x) + x * 292 + x * (-x)\)
= \(61804 - 212x + 292x - x^2\)
= \(-x^2 + 80x + 61804\)
The revenue function is a quadratic function in the form\(R(x) = -x^2 + 80x + 61804\), representing a downward-opening parabola.
To find the x-coordinate of the vertex (which gives the number of passengers for maximum revenue), use the formula \(x = -b/2a\), where \(a = -1\) and \(b = 80\).
\(x=\frac{-80}{2*(-1)}\)
\(= \frac{80}{2}\)
\(= 40\)
Therefore, the number of passengers above 212 for maximum revenue is 40.
Substitute x = 40 into the revenue function to find the maximum revenue:
\(R(x) = -(40)^2 + 80(40) + 61804\)
\(= -1600 + 3200 + 61804\)
\(= 61804 + 1600\)
\(= 63404\)
Hence, the maximum revenue is $63,404.
To determine the fare per passenger, subtract x from the base fare of $292:
Fare per passenger = Base fare - x
\(= 292 - 40\)
\(= 252\) Dollars per passenger.
The left and right page numbers of an open book are two consecutive integers whose sum is 533. Find the page numbers
Answers
Answer:
The page numbers are 266 and 267
Step-by-step explanation:
I divided 533 by 2
Then get 266.5
Then guessed and checked which pages around that value added up to 533
and you get pages 266 and 267
Which number is equal to 6^3?
A. 18
B. 36
C. 216
D. 666
Answers
Answer:
C. 216
Step-by-step explanation:
6³ = 6 x 6 x 6
6 x 6 = 36
36 x 6 = 180 + 36
180 + 36 = 216
hope this helps
6•6=36
36•6=216
Whats -20x 50????????????
Answers
Answer:
-1,000
Step-by-step explanation:
Answer:
The answer is -1000
Step-by-step explanation:
Hope this helps!
1) Find the perimeter of the composite figure.
A) 23.5
B) 42.9
C) 46.9
D) 31.9
2) Find the area of the composite figure.
A) 64.25
B) 42.95
C) 39.5
D) 103.5

Answers
1) The perimeter of the composite figure is 31.9
2) The area of the composite figure is 64.25
What is perimeter?
The complete length of a shape's edge serves as its perimeter in geometric terms. Adding the lengths of all the sides and edges that surround a form yields its perimeter. It is calculated using linear length units such centimeters, meters, inches, and feet.
There are 2 shapes: half circle and right triangle
diameter of half circle ,d=10
radius, r=d/2 = 10/2 = 5
Perimeter of half circle = π r = 3.14 * 5 = 15.7
In the right triangle,
base = 5, line perpendicular to base = 10
hypotenuse² = squares of other 2 sides added
= 5² + 10²
= 25 +100
= 125
hypotenuse = ± √125 = ±11.18
consider positive for length
hypotenuse = 11.18
The perimeter of the composite figure
= Perimeter of half circle +base of right triangle + hypotenuse of right triangle
=15.7 + 5 + 11.18
= 31.9
Area of half circle = 0.5*π *r² = 0.5*3.14*5² = 39.25
Area of right triangle = 0.5*base * height
= 0.5*5*10
= 25
The area of the composite figure
=Area of half circle + Area of right triangle
= 39.25 + 25
= 64.25
To learn more about the perimeter form the link:
https://brainly.com/question/19819849
#SPJ1
Marco budgets $1,600 a month for expenses.
According to the graph, how much does he pay
for his credit card, groceries, and rent?
$1,008
$908
$1,142
$1,029
Answers
Marco pays $1008 for for his credit card, groceries, and rent.
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity.
Given that Marco budgets $1,600 a month for expenses.
According to the graph he pays 4% of credit card
Now let us find 4% of 1600
4/100×1600
0.04×1600
$64 Marco pays for credit card.
From graph, he pays 17% for groceries
17% of 1600
17/100×1600
0.17×1600=$272
$272 Marco pays for Groceries.
From graph, he pays 42% for rent
42/100×1600
0.42×1600=672
$672 Marco pays for Rent.
Hence, Marco pays $1008 for for his credit card, groceries, and rent.
To learn more on Percentage click:
brainly.com/question/28269290
#SPJ1
Name the image of R(1, 2) after a 270 rotation about (0, - 2)
Answers
The image after a 270 rotation is (4, -3)
How to determine the image after rotation about a point?
If the point of rotation is not the origin, the steps are as follows:
1. Subtract the point of rotation off each vertex point of
the shape
2. Rotate as you would around the origin
3. Add the point of rotation back to each vertex point of
the shape
Given: R(1, 2) after a 270 rotation about (0, - 2)
step1: (1-0, 2-(-2)) = (1, 4)
step 2: For rotation about the origin through 270°, the image is (y, -x). Thus, (1, 4) => (4, -1)
step 3: (4, -1) => (4+0, -1+(-2) ) = (4, -3)
Therefore, the image of R(1, 2) after a 270 rotation about (0, - 2) is (4, -3)
Learn more about rotation on:
brainly.com/question/29321467
#SPJ1
1 3/4 divided by 1/2-1 1/2 to the 3rd
Answers
Answer:
-7/4
1/8
Step-by-step explanation:
1. If the problem is; (1 3/4) / (1/2 - 1 1/2)^(3)
(a). Convert to improper fractions;
(7/4) / (1/2 - 3/2)^3
(b). Simplify;
(7/4) / (-2/2)^3
(7/4) / (-1)^3
(7/4) / (-1)
-7/4
2. If the problem is; ((1 3/4) / (1/2)) - (1 1/2)^3
(a). Convert to improper fractions;
((7/4)/ (1/2)) - (3/2)^3
(b). Simplify;
((7/4)/ (1/2)) - (3/2)^3
((7/4)*(2/1)) - (27/8)
(7/2) - (27/8)
(28/8) - (27/8)
1/8
The interest on an investment varies directly as the rate of interest. If the interest is $48 when the interest rate is 10%, find the interest when the rate is 4.3%
Answers
Answer:
48×4.3=184 and that is the easy way how to do it
Is 3/7 closet to 0, 1/2 or 1
Answers
Answer:
1/2
Step-by-step explanation:
if you divide them you get about 42 and after you round it,it's closer to 50%
Answer:
1/2 is closest to 0
Step-by-step explanation:
Keith 1,342 cupcake rounds to 1,300 and joe 1,347 cupcake rounds to 1,350 who round to the nearest hundred?
Answers
Answer:
Keith
Step-by-step explanation:
When you are rounding to the nearest hundred it would NOT include a tens or ones value. So in this case 1,300 would be correct.
Hope that helps and have a great day!
Find the LCD for the following pair of fractions.
1/8
and
7/9
The least common denominator is
Answers
Answer:
The least common denominator is 72.
Step-by-step explanation:
8 = 2³
9 = 3²
Since the two denominators have no common factors, the LCD is their product.
LCD = 8 × 9 = 72
The least common denominator is 72.
Recall that with base-ten blocks: 1 long 10 units, 1 flat 10 longs, and 1 block 10 flats. What is the fewest number of multibase blocks that can be used to represent the corresponding numeral in the given base?
a. 20 longs in base seven
b. 10 longs in base three
Answers
a. The answer is: The fewest number of multibase blocks required to represent 20 longs in base seven is 2 flats.
b. The answer is: The fewest number of multibase blocks required to represent 10 longs in base three is 3 flats and 1 unit.
a. To represent 20 longs in base seven, we need to find the fewest number of multibase blocks required.
In base seven, we have the following conversions:
1 long = 1 unit
1 flat = 10 units
1 block = 10 flats
To represent 20 longs, we can use 2 flats (each flat representing 10 units) and 0 units since there are no remaining units.
So, the fewest number of multibase blocks required would be 2 flats.
Therefore, the answer is: The fewest number of multibase blocks required to represent 20 longs in base seven is 2 flats.
b. To represent 10 longs in base three, we need to find the fewest number of multibase blocks required.
In base three, we have the following conversions:
1 long = 1 unit
1 flat = 3 units
1 block = 3 flats
To represent 10 longs, we can use 3 flats (each flat representing 3 units) and 1 unit since there is one remaining unit.
So, the fewest number of multibase blocks required would be 3 flats and 1 unit.
Therefore, the answer is: The fewest number of multibase blocks required to represent 10 longs in base three is 3 flats and 1 unit.
for such more question on fewest number
https://brainly.com/question/859564
#SPJ8