Find the following Taylor expansions about x = a for each of the following functions and their associated radii of convergence. (a) f(x) = e^{5x}, a = 0. (b) f(x) = sin(πx), a =1.
Answers
(a) The Taylor series expansion of f(x) = e^{5x} about x = 0 is Σ(n=0 to ∞) [(5^n)/(n!)]x^n, with radius of convergence = ∞.
(b) The Taylor series expansion of f(x) = sin(πx) about x = 1 is Σ(n=0 to ∞) (-1)^n π^(2n+1)/(2n+1)!^(2n+1), with radius of convergence = 1.
(a) To find the Taylor series expansion of e^{5x} about x = 0, we can use the formula for the Taylor series of e^x, substituting 5x for x, to get:
e^{5x} = Σ(n=0 to ∞) [(5x)^n/n!] = Σ(n=0 to ∞) [(5^n)/(n!)]x^n
The radius of convergence of this series is ∞, because the ratio of consecutive terms is (5x)/(n+1), which approaches 0 as n approaches infinity for any finite x.
(b) To find the Taylor series expansion of sin(πx) about x = 1, we can use the formula for the Taylor series of sin(x), substituting π(x-1) for x, to get:
sin(πx) = Σ(n=0 to ∞) (-1)^n π^(2n+1)/(2n+1)!^(2n+1)
The radius of convergence of this series is 1, because the ratio of consecutive terms is π(x-1)/(2n+1), which approaches π as n approaches infinity for x = 1, and is greater than π for x > 1, causing the series to diverge.
To know more about Taylor series click here:
https://brainly.com/question/29733106
#SPJ11
Related Questions
expression z divide by 5 then add 3
Answers
Answer:
x
5
Step-by-step explanation:
First choose a variable to represent the number,
Let's call it
x
We need to divide that number by
5
x
÷
5
or
x
5
is how you write it as an expression.
for what values of t can 10x^2+tx+8 be written as the product of two binomials
I NEED ASAP
Answers
We can write the quadratic expression 10x^2 + tx + 8 as:
10x^2 + tx + 8 = 10x^2 + (a+b)x + ab
where a and b are constants that we want to determine, and (a+b)x is the middle term in the quadratic expression.
We can factor 10 as 25 and 8 as 22*2, so we have:
10x^2 + tx + 8 = (2x + c)(5x + d)
where c and d are the constants that we need to determine.
Expanding the right-hand side of this equation, we get:
(2x + c)(5x + d) = 10x^2 + (2d+5c)x + cd
Comparing this to the original expression, we see that:
2d + 5c = t
cd = 8
We can use these equations to solve for c and d in terms of t:
c = (t - 2d)/5
d = 8/c
Substituting d in terms of c in the first equation, we get:
2(8/c) + 5c = t
Multiplying through by c, we get a quadratic equation in c:
16 + 5c^2 = tc
We want this equation to have real solutions for c, so the discriminant must be non-negative:
25t^2 - 80 >= 0
Solving this inequality for t, we get:
t <= -8/5 or t >= 8/5
Therefore, the quadratic expression 10x^2 + tx + 8 can be written as the product of two binomials for all values of t less than or equal to -8/5 or greater than or equal to 8/5.
Can someone please help me asap I’ll mark brainlist!!?!?

Answers
Answer:
32/13
Step-by-step explanation:
2 6/13
2(13)=26
26+6=32
32/13
Answer:
32/13
Step-by-step explanation:
13x2=26
26+6=32
Denominator stays the same
ABC company has just purchased a life truck that has a useful life of 5 years. The engineer estimates that maintenance costs for the truck during the first year will be $2,000. As the truck ages, maintenance costs are expected to increase at a rate of $300 per year over the remaining life. Assume that the maintenance costs occur at the end of each year. The firm wants to set up a maintenance account that earns 10% interest per year. All future maintenance expenses will be paid out of this account. How much does the firm have to deposit in the account now? $9,640.11
$11,500.00
$9,920.21
$9,127.02
Answers
The amount the firm needs to deposit in the account now is 9,640.11. Given that the company has purchased a life truck with a useful life of 5 years, the maintenance costs for the truck during the first year are 2,000.
Also, maintenance costs are expected to increase at a rate of 300 per year over the remaining life, which is for four years. Assume that the maintenance costs occur at the end of each year.
The future maintenance costs for the truck can be calculated as shown below:
Year 1:\($2,000Year 2: $2,300Year 3: $2,600Year 4: $2,900Year 5: $3,200\)The maintenance account that earns 10% interest per year has to be set up, and all future maintenance expenses will be paid out of this account. The future value of the maintenance costs, i.e., the amount that the firm needs to deposit now to earn 10% interest and pay the maintenance costs over the next four years is given by:
\(PV = [C/(1 + i)] + [C/(1 + i)²] + [C/(1 + i)³] + [C/(1 + i)⁴] + [(C + FV)/(1 + i)⁵]\),where PV is the present value of the future maintenance costs, C is the annual maintenance cost, i is the interest rate per year, FV is the future value of the maintenance costs at the end of year 5, which is $3,200, and 5 is the total number of years, which is
5.Substituting the given values in the above equation:
\(PV = [2,000/(1 + 0.1)] + [2,300/(1 + 0.1)²] + [2,600/(1 + 0.1)³] + [2,900/(1 + 0.1)⁴] + [(3,200 + 3,200)/(1 + 0.1)⁵] = 9,640.11\)Therefore, the firm needs to deposit 9,640.11 in the account now. Hence, option (A) is the correct answer.
To know more about amount visit:
https://brainly.com/question/32453941
#SPJ11
what central idea about mathematical instruction does the author express in passage 1?
Answers
An all-night study session can help you catch up on school assignments. The only way to become a straight-A student is efficient study habits.
Most students pseudo-work and end up wasting valuable time.
The correct option is (C)
This is based on an article about pseudo-working which is something that students do where they read for long hours and appear very serious in reading when in fact they do not focus on the reading and therefore end up not grasping much.
The author was trying to express that most students do this and that it is simply a waste of time which could have been spent actually studying.
The correct option is (C).
Learn more about Article at:
https://brainly.com/question/14172780
#SPJ4
The given question is incomplete, complete question is:
What central idea about studying does the author express in Passage 1?
A Straight-A students know how to work harder than other students.
B The only way to become a straight-A student is efficient study habits.
C Most students pseudo-work and end up wasting valuable time.
D An all-night study session can help you catch up on school assignments.
Prof. Okamoto selects 3 different students to report on 3 different current events. If there are 25 students in the class, in how
many ways can Professor Okamoto make the selection?
2. Consider the following.
(a) In how many different ways can a player select a diamond and a spade from a deck of 52 bridge cards?
(b) In how many different ways can a player select one card of each suit from a bridge deck?
3. Perform the computation.
P(60, 3')
4. Is the following pair of sets equal?
A = {9, 18, 27, 36}
B = (x | x is a multiple of 9}
Yes, the sets are equal.
No, the sets are not equal.
Answers
There are 2,300 ways for Professor Okamoto to make the selection. There are 169 different ways to select a diamond and a spade from a deck of 52 bridge cards.
1. To select 3 different students out of 25, we can use the combination formula. The number of ways to select 3 students from a set of 25 is given by:
C(25, 3) = 25! / (3!(25-3)!) = 25! / (3!22!) = (25 * 24 * 23) / (3 * 2 * 1) = 25 * 4 * 23 = 2,300.
Therefore, there are 2,300 ways for Professor Okamoto to make the selection.
2. (a) To select a diamond and a spade from a deck of 52 bridge cards, we can use the multiplication principle. There are 13 diamonds and 13 spades in a deck, so the number of ways to select one diamond and one spade is:
13 * 13 = 169.
Therefore, there are 169 different ways to select a diamond and a spade from a deck of 52 bridge cards.
(b) To select one card of each suit from a bridge deck, we can again use the multiplication principle. There are 13 cards in each suit (diamonds, spades, hearts, and clubs), so the number of ways to select one card from each suit is:
13 * 13 * 13 * 13 = 28,561.
Therefore, there are 28,561 different ways to select one card of each suit from a bridge deck.
3. P(60, 3) represents the number of permutations of 60 objects taken 3 at a time. The formula for permutations is:
P(n, r) = n! / (n - r)!
Using this formula, we can calculate:
P(60, 3) = 60! / (60 - 3)! = 60! / 57! = 60 * 59 * 58 = 205,320.
Therefore, P(60, 3) is equal to 205,320.
4. The sets A and B are not equal. Set A contains the elements {9, 18, 27, 36}, while set B represents the set of all multiples of 9. Since set B includes all multiples of 9, it would also include numbers like 45, 54, 63, and so on, which are not present in set A. Therefore, the sets A and B are not equal.
To learn more about permutations click here:
brainly.com/question/31769573
#SPJ11
There are 2,300 ways for Professor Okamoto to make the selection. There are 169 different ways to select a diamond and a spade from a deck of 52 bridge cards.
1. To select 3 different students out of 25, we can use the combination formula. The number of ways to select 3 students from a set of 25 is given by:
C(25, 3) = 25! / (3!(25-3)!) = 25! / (3!22!) = (25 * 24 * 23) / (3 * 2 * 1) = 25 * 4 * 23 = 2,300.
Therefore, there are 2,300 ways for Professor Okamoto to make the selection.
2. (a) To select a diamond and a spade from a deck of 52 bridge cards, we can use the multiplication principle. There are 13 diamonds and 13 spades in a deck, so the number of ways to select one diamond and one spade is:
13 * 13 = 169.
Therefore, there are 169 different ways to select a diamond and a spade from a deck of 52 bridge cards.
(b) To select one card of each suit from a bridge deck, we can again use the multiplication principle. There are 13 cards in each suit (diamonds, spades, hearts, and clubs), so the number of ways to select one card from each suit is:
13 * 13 * 13 * 13 = 28,561.
Therefore, there are 28,561 different ways to select one card of each suit from a bridge deck.
3. P(60, 3) represents the number of permutations of 60 objects taken 3 at a time. The formula for permutations is:
P(n, r) = n! / (n - r)!
Using this formula, we can calculate:
P(60, 3) = 60! / (60 - 3)! = 60! / 57! = 60 * 59 * 58 = 205,320.
Therefore, P(60, 3) is equal to 205,320.
4. The sets A and B are not equal. Set A contains the elements {9, 18, 27, 36}, while set B represents the set of all multiples of 9. Since set B includes all multiples of 9, it would also include numbers like 45, 54, 63, and so on, which are not present in set A. Therefore, the sets A and B are not equal.
To learn more about permutations click here: brainly.com/question/31769573
#SPJ11
A researcher interviews 6 widows about their marriages and notices how many cats are wandering around. Is there a significant relationship between the number of times an old widow was married and the number of cats the old lady owns? ( You don't need to do the math to calculate it - the Pearson r is given).
Times Married: 1 1 2 2 3 3
Cats Owned: 3 2 4 5 5 6
Pearson r = +.91
Write up the conclusion for this study in APA format and be sure to include the r2.
Answers
There is a significant relationship between the number of cats she owns and the number of times an old widow was married (r = +0.91, p < 0.05, r² = 0.82).
Given, the Pearson correlation coefficient of +0.91,
There appears to be a strong +ve correlation between the number of cats she owns and the number of times an old widow was married.
It suggests that the more times a widow was married,the more cats she tends to own.
Approximately 82% of the variance in the number of cats owned can be explained by the number of times a widow was married is indicated by the coefficient of determination (r²).
Hence, we can say that there is a significant relationship between the number of cats she owns and the number of times an old widow was married (r = +0.91, p < 0.05, r² = 0.82).
Learn more about Pearson correlation coefficient here,
https://brainly.com/question/31801929
#SPJ4
Need help!
Hey does anybody mind helping me with this question? It’s in the picture also tysm if u answer I will mark u Brainly back!!! Have a great day everyone

Answers
Answer:
8/11
Step-by-step explanation:
2 2/3+3 2/3
2+3 + 2/3+2/3
5 + 4/3
5 + 1 1/3
6 1/3
The third one is your answer, also thank you. I hope you have a great day as well.
comeplete using distributive property (x+2x+3x)(x+4)
Answers
Answer:
6x^2 + 24x
Step-by-step explanation:
Help!!! can someone answer these, Thank You!

Answers
Use the Pythagorean Theorem to find the missing length. Round your answer to the
nearest tenth.

Answers
In this triangle it is clear that the unknown side x is the hypotenuse of both the triangles that are being formed . So , let us take any one of the triangles and with it's length let us find the length of their hypotenuse which is side x .
= 5² + 5² = x² ( according to the pythagorean theorem the square on the hypotenuse will be equal to the sum of the squares on the other two legs )
= 25 + 25 = x²
= 50 = x²
= 7.0710678119 = x
But they have given that we have to round it off to the nearest tenths , so ;
= 7.0710678119 will be equal to = 7.10
= 7.1 = x
Therefore , the length of the unknown side x = 7.1 .
If the nth term of a sequence is
12n - 6 what is the 8th term?
Answers
Answer:
i think the answer is 90
Step-by-step explanation:
i hope this helped you have a nice day :)
you are going to a 4-year college in 4 years that will cost $14,895.00 yr. your parents expect you to pay 5% of the total cost. 3. how much do you need to pay for each year of attending?
Answers
According to the given data total cost of attending college would be $744.75.
If the total cost of attending the 4-year college is $14,895.00 per year and your parents expect you to pay 5% of the total cost, you would need to calculate 5% of $14,895.00 for each year.
To calculate the amount you need to pay for each year, you can use the following formula:
Payment per year = (Percentage to pay / 100) * Total cost per year
Let's calculate it:
Payment per year = (5 / 100) * $14,895.00
Payment per year = 0.05 * $14,895.00
Payment per year = $744.75
Therefore, you would need to pay $744.75 for each year of attending the college.
Learn more about data:https://brainly.com/question/179886
#SPJ11
PLZ HELP 100 POINTS AND DONT BE MEAN

Answers
Answer:
Full drum 80 dollars
one lid missing
earn 10 dollars less
Step-by-step explanation:
We need to find the surface area
SA = 2 pi r^2 + 2 pi rh
The diameter is 2 so the radius = 2/2 =1
SA = 2 * pi * 1^2 + 2 * pi * 1 * 3
= 2 pi + 6pi
= 8pi
Using pi = 3.14
SA = 8 *3.14 = 25.12 ft^2
We get 3.18 per ft^2
25.12 * 3.18 =79.88
To the nearest dollar
80 dollars
If one of the lids is missing
SA = pi r^2 + 2 pi rh
pi + 6pi
7 pi
Using pi = 3.14
SA = 7 *3.14 = 21.98 ft^2
We get 3.18 per ft^2
21.98 * 3.18 =69.90
To the nearest dollar
70
The difference is 10 dollars
Answer:
\(\Huge \boxed{\mathrm{a) \ \$ \ 80}} \\\\\\\\ \Huge \boxed{\mathrm{b) \ \$ \ 10}}\)
\(\rule[225]{225}{2}\)
Step-by-step explanation:
Surface area of the cylinder :
2πr² + 2πrh
The diameter is 2 ft, so the radius is 1 ft.
⇒ 2π(1)² + 2π(1)(3)
⇒ 8π ≈ 25.13
$3.18 is getting payed per square foot.
⇒ 25.13 × 3.18
⇒ 79.9221171073 ≈ 80
If the lid was missing:
πr² + 2πrh
π(1)² + 2π(1)(3)
7π ≈ 21.99
$3.18 is getting payed per square foot.
⇒ 21.99 × 3.18
⇒ 69.9318524689 ≈ 70
The difference :
80 - 70 = 10
$10 less if the lid is missing.
\(\rule[225]{225}{2}\)
Find the surface area of the composite solid.

Answers
The area of the composite solid in the image given is: 399.6 m².
What is the Surface Area of a Composite Solid?The surface are of the composite solid = area of the 3 triangular face of the top solid + area of the triangular base of the bottom solid + 3(area of rectangular face of the bottom solid).
Area of the 3 triangular face of the top solid = 3(1/2bh) = 3(1/2 × 8 × 7) = 84 m²
Area of the triangular base of the bottom solid = 1/2bh = 1/2 × 8 × 6.9 = 27.6 m²
3(area of rectangular face of the bottom solid) = 3(length × width) = 3(12 × 8) = 288 m²
Surface area of the solid = 84 + 27.6 + 288 = 399.6 m²
Learn more about surface area of composite solids on:
https://brainly.com/question/17065613
#SPJ1
Find the value of each variable. Write your answer in simplest radical form.

Answers
Hopefully you understand

A project under consideration has a 10-year projected life. The initial investment for the project is estimated to have a mean of $10,000 and a standard deviation of $1,000. The annual receipts are independent, with each year’s expected return having a mean of $1,800 and a standard deviation of $200. MARR is 12 percent. Assuming that initial investment and annual receipts are independent and normally distributed, estimate the probability that the present worth is negative using NORM.INV function in excel.
Answers
This value represents the present worth below which the probability is 0.5, indicating a negative present worth.
To estimate the probability that the present worth is negative using the NORM.INV function in Excel,
we need to calculate the present worth of the project and then determine the corresponding probability using the normal distribution.
The present worth of the project can be calculated by finding the sum of the present values of the annual receipts over the 10-year period, minus the initial investment. The present value of each annual receipt can be calculated by discounting it back to the present using the minimum attractive rate of return (MARR).
Using the given information, the present value of the initial investment is $10,000. The present value of each annual receipt is calculated by dividing the expected return of $1,800 by \((1+MARR)^t\),
where t is the year. We then sum up these present values for each year.
We can use the NORM.INV function in Excel to estimate the probability of a negative present worth. The function requires the probability value, mean, and standard deviation as inputs.
Since we have a mean and standard deviation for the present worth,
we can calculate the corresponding probability of a negative present worth using NORM.INV.
This value represents the present worth below which the probability is 0.5. By using the NORM.INV function,
we can estimate the probability that the present worth is negative based on the given data and assumptions.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ4
evaluate ∫30(4f(t)−6g(t)) dt given that ∫150f(t) dt=−7, ∫30f(t) dt=−8, ∫150g(t) dt=4, and ∫30g(t) dt=8
Answers
The evaluation of ∫30(4f(t) - 6g(t)) dt given that ∫150f(t) dt = -7, ∫30f(t) dt = -8, ∫150g(t) dt = 4, and ∫30g(t) dt = 8 is -80.
Given that ∫150f(t) dt = -7, ∫30f(t) dt = -8, ∫150g(t) dt = 4, and ∫30g(t) dt = 8.
Let us evaluate ∫30(4f(t) - 6g(t)) dt.
Therefore,∫30(4f(t) - 6g(t)) dt = ∫30(4f(t) dt - 6g(t) dt) = 4 ∫30f(t) dt - 6 ∫30g(t) dt
Now, using the given values in the question we can say that,∫30(4f(t) - 6g(t)) dt = 4 ∫30f(t) dt - 6 ∫30g(t) dt = 4 (-8) - 6(8) = -32 - 48 = -80
Therefore, the evaluation of ∫30(4f(t) - 6g(t)) dt given that ∫150f(t) dt = -7, ∫30f(t) dt = -8, ∫150g(t) dt = 4, and ∫30g(t) dt = 8 is -80.
Note: The given integrals ∫150f(t) dt, ∫30f(t) dt, ∫150g(t) dt, and ∫30g(t) dt are only intermediate steps in order to evaluate the final integral.
Know more about integrals here,
https://brainly.com/question/31433890
#SPJ11
A circle has a circumference of 7{,}8507,8507, comma, 850 units. What is the radius of the circle?
Use 3. 14 for pi and enter your answer as a decimal
Answers
7,850 = 2 * 3.14 * r
Now, we'll solve for r:
7,850 = 6.28 * r
r = 7,850 / 6.28
r ≈ 1,250
So, the radius of the circle is approximately 1,250 units.
The measures of two complementary angles are described by the expressions (11x−11)° and (16x−7)°. Find the measures of the angles.I know complementary when their measures add to 90 degrees. but I'm not to sure where to plug the numbers in
Answers
Given:
\((11x-11)^{\circ}and(16x-7)^{\circ}\text{ forms an complementary angles.}\)\(\begin{gathered} 11x-11+16x-7=90 \\ 27x-18=90 \\ 27x=90+18 \\ 27x=108 \\ x=\frac{108}{27} \\ x=4 \end{gathered}\)what is 20×0+2983-0÷176+827-9 equal .
Answers
We are asked to evaluate:
20×0+2983-0÷176+827-9
We use the order of operations where the products and divisions are performed first, and additions and subtractions LAST.
20 x 0 = 0
0 divided by 176 ia zero as well = 0
therefore now that multiplications and divisions are taken care of, we evaluate the additions and subtractions:
0 + 2983 - 0 + 827 - 9 = 3801
So please type 3801 as the answer.
can you show me exactly were to plot these?
Answers
1. Find the length of each leg.
R
Q
30⁰
4
60%
P

Answers
Answer:
QP = 2
QR = 2√3
Step-by-step explanation:
This is a special right triangle with angle measures as follows:
30° - 60° - 90°
And side lengths represented with:
x - x√3 - 2x respectively to angle measures.
The side length that sees angle measure 90, hypotenuse, is given as 4 so the legs would be:
2 and 2√3
Solve: x2=925 A x=35 B x=−35 C x=325 and x=−325 D x=35 and x=−35
THE ANSWER IS D
Answers
Answer:
D? i prob got it wrong
Step-by-step explanation:
Answer:
well thx for the answer
Step-by-step explanation:
....................

Answers
Answer:
2/6
Step-by-step explanation:
Determine the minimum sample size required when you want to be onfident that the sample mean is within one unit of the population mean and 13.8 assume the population is normally distributed.
Answers
The minimum sample size required when you want to be 99% confident that the sample mean is within one unit of the population mean and σ = 13.8 is 1268
Given: To find the minimum sample size, confidence level = 99%, standard deviation = 13.8, and one unit population mean. [Normally distributed]
Solving the given question:
We know that the formula for Margin of error is:
Margin of error = z-score * (standard deviation) / root (sample size)
E = z * σ / √(n), where
E = Margin of error
z = z-score
n = Sample size
σ = standard deviation
Therefore, sample size = ( z – score * standard deviation / margin of error)²
n = ( z * σ / E )²
First, calculate the z-score for the 99% confidence level.
From the normal distribution curve, the area under 99% confidence level is given as:
Area under 99% confidence level = (1 + confidence level) / 2 = (1 + 0.99) / 2 = 0.995
From the z-score table, we find the value of z with the corresponding area of 0.995
We find the value of the z-score corresponding to 0.995 is 2.58
Also given sample mean is one unit of the population. So the margin of error is 1
E = 1
And given Standard deviation = 13.8
σ = 13.8
Putting the values in the given formula of sample size n =
n = (2.58 * 13.8 / 1 )²
n = 1267.64
n = 1268
Hence the minimum sample size required when you want to be 99% confident that the sample mean is within one unit of the population mean and σ = 13.8 is 1268
Know more about “normal distribution” here: https://brainly.com/question/15103234
#SPJ4
Disclaimer: Determine the minimum sample size required when you want to be 99% confident that the sample mean is within one unit of the population mean and G = 13.8. Assume the population is normally distributed. A 99% confidence level requires a sample size of (Round up to the nearest whole number as needed )
Solve using the quadratic formula: 5x2 + 5x = -5
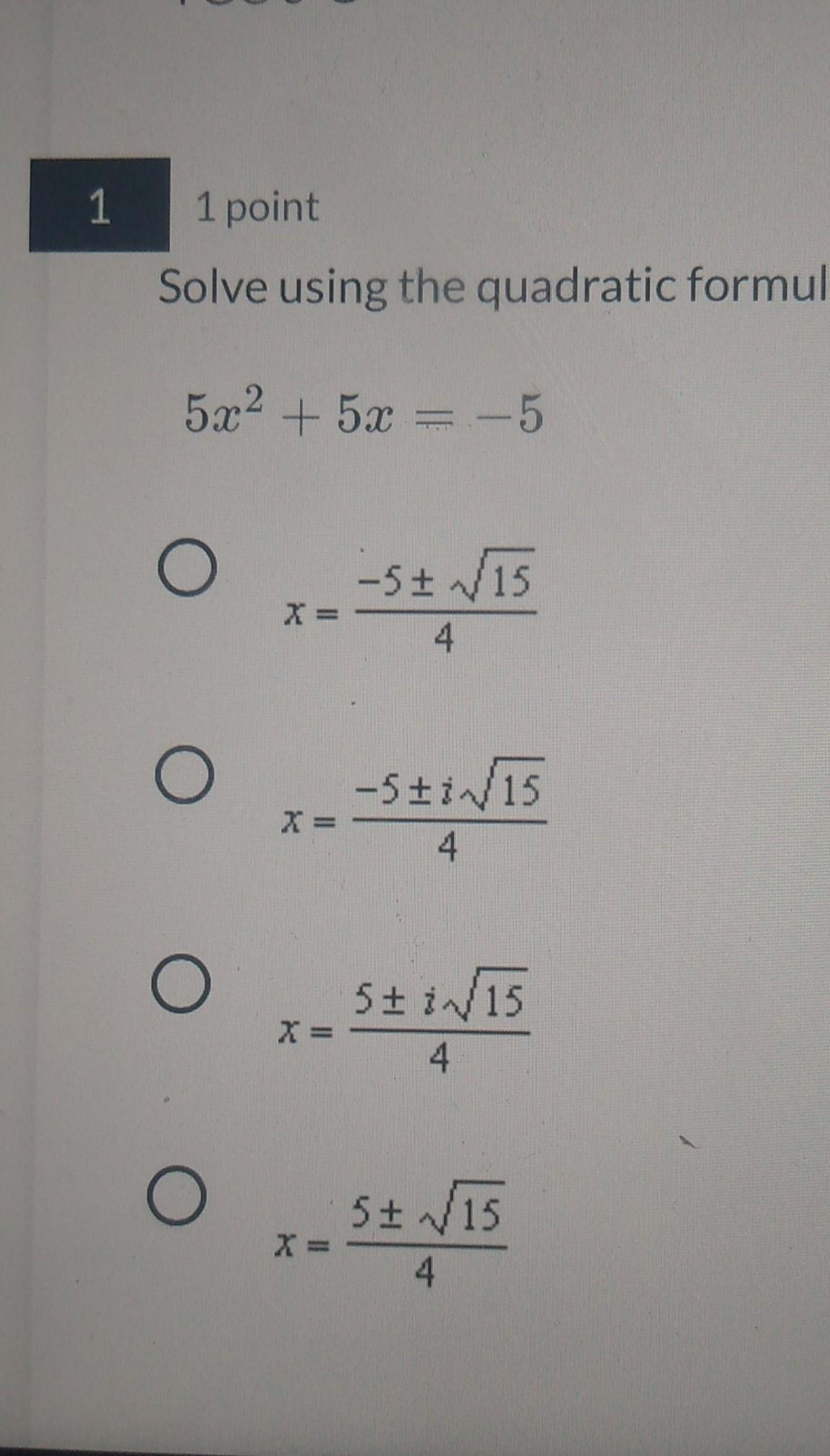
Answers
The second option is the correct one.
Because includes -5 and ( i ) in it
the average of 8 girls is 15 and the average of 6 girls is 13 find the average of the other two girls with equal age
Answers
Answer:
21
Step-by-step explanation:
Since the girls have the same age, let their age be x.
Then, their average is
\(\frac{x+x}{2} = \frac{2x}{2} = x\)
Let \(S_{i}\) denote the age of 'i' girls.
Then, \(S_{8} = S_{6} + x + x - eq(1)\)
Also, we have,
\(\frac{S_{8}}{8} =15 - eq(2)\)
\(\frac{S_{6}}{6} =13 - eq(3)\)
Then eq(2):
(from eq(1) and eq(3))
\(\frac{S_{6} + 2x}{8} =15\\\\\frac{13*6 + 2x}{8} = 15\\\\78+2x = 120\\\\2x = 120-78\\\\x = 21\)
The average of the other two girls with equal age is 21
A correlation coefficient of \( -0.84 \) between the variables "impulsivity" and "hours spent viewing TV" indicates A weak relationship \& the more impulsive, the less TV viewing A strong refationship
Answers
The correlation coefficient of -0.84 between the variables "impulsivity" and "hours spent viewing TV" indicates a strong relationship, suggesting that the more impulsive an individual is, the less time they spend viewing TV.
What does a correlation coefficient of -0.84 indicate about the relationship between impulsivity and hours spent viewing TV?The correlation coefficient measures the strength and direction of the linear relationship between two variables. In this case, a correlation coefficient of -0.84 indicates a strong negative relationship between impulsivity and hours spent viewing TV.
The negative sign indicates an inverse relationship, meaning that as one variable (impulsivity) increases, the other variable (hours spent viewing TV) decreases.
The magnitude of -0.84 indicates a relatively strong relationship. Since the correlation coefficient is close to -1, it suggests that there is a strong tendency for individuals with higher levels of impulsivity to spend less time viewing TV.
Conversely, those with lower levels of impulsivity tend to spend more time watching TV.
Learn more about correlation coefficient
brainly.com/question/29978658
#SPJ11
1. Vocabulary Explain how to isolate the variable in the equation
-1/2n+7=15. Lesson 5-2
M
CH
Answers
The Variable of equation -1/2n + 7 = 15 is 'n' .
Variable Isolation :Isolating a variable means rearranging an algebraic equation so that a different variable is on its own.
Given equation,
-1/2n + 7 = 15
Variable :
A variable is an alphabet or term that represents an unknown number or unknown value or unknown quantity.
The variables are specially used in the case of algebraic expression or algebra.
So, Variable of above equation = 'n'
To learn more about Variable visit :
https://brainly.com/question/14706863
#SPJ9