Find the first four nonzero terms of the Taylor series about 0 for the function f(x) =√1-3x. Note that you may want to find these in a manner other than by direct differentiation of the function.
Answers
To find the first four nonzero terms of the Taylor series about 0 for the function f(x) = √(1-3x), we can use the binomial series expansion method. This is because the given function has a form similar to (1 + kx)^n, where n is a rational number.
In our case, n = 1/2 and k = -3, so we have f(x) = (1 - 3x)^(1/2). The binomial series expansion formula is:
(1 + kx)^n = 1 + n(kx) + [n(n-1)/2!](kx)^2 + [n(n-1)(n-2)/3!](kx)^3 + ...
Now, we plug in the values n = 1/2 and k = -3 into the formula:
(1 - 3x)^(1/2) = 1 + (1/2)(-3x) + [(1/2)(1/2-1)/2!](-3x)^2 + [(1/2)(1/2-1)(1/2-2)/3!](-3x)^3 + ...
Simplify the terms:
= 1 - (3/2)x + (3/8)x^2 - (1/16)x^3 + ...
So, the first four nonzero terms of the Taylor series about 0 for the function f(x) = √(1-3x) are: 1 - (3/2)x + (3/8)x^2 - (1/16)x^3. What is binomial series: The binomial series enables us to apply the binomial theorem when k is not a positive integer.What is the binomial theorem: The binomial theorem (or binomial expansion) in elementary algebra describes the algebraic expansion of binomial powers.The binomial theorem states that for some a,b∈R and some k ∈Z+ ,(a+b)k=∑n=0k(kn)ak−nbn. The binomial series allows us to use the binomial theorem for instances when k is not a positive integer.What is Binomial Expansion: An expression that has been raised to any finite power can be expanded using the binomial theorem. A useful expansion technique with applications in probability, probability theory, and algebra is the binomial theorem. A binomial expression is an algebraic expression with two terms that are not the same.
Learn More About binomial theorem: https://brainly.com/question/22233145
#SPJ11
Related Questions
using only words solve 8x+3=27 step by step
Answers
Answer:
X=3
Step-by-step explanation:
Subtract 3 from both sides
Simplify 27-3 to 24
Divide both sides by 8
Simplify 24/8 to 3
Step-by-step explanation:
Your goal is to isolate x, so your first step is to subtract by 3 on both sides. That leaves you with the equation 8x=24. Divide by 8 on both sides (since x is being mutliplied b 8) and you get x=3
plz answer the picture below fast and correctly!

Answers
Answer:
a) BOC = 80⁰
b) COD = 60⁰
Step-by-step explanation:
..................
Answer:
BOC is 80 and COD is 60
Step-by-step explanation:
If DOF is 120 you subtract 40 from it because of of AOB then COD is the remaining of 180
A company had returns of 5%, 10%, -15%, 20%, -12%, 22%, 8% in
the last few years. Compute the arithmetic average return,
geometric average return, variance, and standard deviation of
returns.
Refer to
Answers
Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
Given, Returns of the company for the last few years are 5%, 10%, -15%, 20%, -12%, 22%, 8%
Arithmetic Average return:
Arithmetic Average return = (sum of all returns) / (total number of returns)
Arithmetic Average return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Therefore, the arithmetic average return of the company is 2.57%.
Geometric average return:
Geometric average return = [(1+R1) * (1+R2) * (1+R3) * …….. * (1+Rn)]1/n - 1
Geometric average return = [(1.05) * (1.1) * (0.85) * (1.2) * (0.88) * (1.22) * (1.08)]1/7 - 1= 0.13
Therefore, the geometric average return of the company is 13%.
Variance:
Variance = (sum of (return - mean return)2) / (total number of returns)
Mean return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Variance = [(5-2.57)2 + (10-2.57)2 + (-15-2.57)2 + (20-2.57)2 + (-12-2.57)2 + (22-2.57)2 + (8-2.57)2] / 7= 392.12 / 7= 56
Therefore, the variance of the company is 56.
Standard Deviation:
Standard Deviation = Square root of Variance
Standard Deviation = √56= 7.48
Therefore, the standard deviation of the company is 7.48%.
Thus, Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
To know more about arithmetic average return, click here
https://brainly.com/question/28562900
#SPJ11
Violet rents a bike in a city she is visiting. She pays an initial fee of $2.50 plus $3.75 per hour she rents the bike. Which equation can be used to find y, the total cost of renting a bike, if x represents the number of hours Violet rents the bike?
Answers
Answer: y = 3.75x + 2.50
Step-by-step explanation:
The equation that can be used to find y, the total cost of renting a bike, if x represents the number of hours Violet rents the bike is:
y = 3.75x + 2.50
Explanation:
Violet pays an initial fee of $2.50, which is a fixed cost that does not depend on the number of hours she rents the bike. Additionally, she pays $3.75 per hour she rents the bike, which is a variable cost that depends on the number of hours. Therefore, the total cost of renting a bike (y) can be expressed as the sum of the fixed cost ($2.50) and the variable cost ($3.75x), which gives the equation:
I need help and show work

Answers
=-7
since it’s two negatives , you’re just adding them
5. ¿Cuál es la expresión algebraica que representa el área de la siguiente figura?
A) 5x + 15
B) 5x + 3
C) 5 + 3x
D) 5x – 15

Answers
A) 5x + 15
Explanation:
5x is the area of the green square (5•x)
15 is the area of the orange rectangle (5 •3 =15)
To have the total area you have to sum the areas of the two figures: 5x + 15
a parabola opening up or down has vertex (-3,2) and passes through (-7, 2/3) . write its equation in vertex form.
Answers
The equation of the parabola in vertex form is y = (-1/12)(x + 3)^2 + 2, which opens downwards since the leading coefficient is negative.
The equation of the given parabola in vertex form is y = a(x + 3)^2 + 2, where a is a constant that depends on whether the parabola opens up or down.
To determine the value of a, we can use the fact that the parabola passes through (-7, 2/3). Substituting these values into the equation, we get:
2/3 = a(-7 + 3)^2 + 2
2/3 = 16a + 2
16a = -4/3
a = -1/12
Therefore, the equation of the parabola in vertex form is
y = (-1/12)(x + 3)^2 + 2.
The vertex form of a parabola is y = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. In this case, we are given that the vertex is (-3, 2), so we can write the equation as y = a(x + 3)^2 + 2.
To find the value of a, we use the fact that the parabola passes through (-7, 2/3). Substituting these values into the equation, we get 2/3 = a(-7 + 3)^2 + 2. Simplifying this equation, we get 2/3 = 16a + 2, which we can solve for a to get a = -1/12.
Therefore, the final equation of the parabola in vertex form is y = (-1/12)(x + 3)^2 + 2, which opens downwards since the leading coefficient is negative.
Learn more about parabola:
brainly.com/question/31142122
#SPJ11
Jane needs $20 to buy her radio. She has saved $15.
What percent of the cost of the radio has she saved?
A. 35%
B. 60%
C. 70%
D. 75%
E. 80%
Answers
Answer:
the answer is d
Step-by-step explanation:
\( \frac{15}{20} \times 100 = 75\)
If the average salary of a computer programmer is $71, 800 with a standard deviation of
13,000, approximately (choose answer) of the programmers make over $97, 800.
Answers
The given average salary is $71,800, with a standard deviation of $13,000.
To find the number of standard deviations above the mean that corresponds to the salary of $97,800, we can use the formula:
Number of standard deviations = (Salary - Mean) / Standard Deviation
Number of standard deviations = ($97,800 - $71,800) / $13,000
Number of standard deviations = $26,000 / $13,000
Number of standard deviations = 2
According to the empirical rule (also known as the 68-95-99.7 rule), approximately 95% of the data falls within two standard deviations of the mean in a normal distribution. This means that approximately 95% of computer programmers make less than $97,800.
Therefore, the approximate percentage of computer programmers who make over $97,800 is (100% - 95%) = 5%.
Approximately 1.5% of computer programmers make over $97,800.
Explanation:The average salary of computer programmers is $71,800 with a standard deviation of $13,000. To determine the percentage of programmers making over $97,800, we need to find the area under the normal distribution curve to the right of this value.
Using the z-score formula, we can find the z-score corresponding to $97,800: z = (x - μ) / σ = (97800 - 71800) / 13000 ≈ 2.145.
Looking up the z-score in a standard normal distribution table, we find that approximately 1.5% of programmers make over $97,800.
Learn more about average salary here:https://brainly.com/question/33849741
#SPJ11
A shoe store uses a 60% markup for all of the shoes it sells. What would be the selling price of a pair of shoes that has a wholesale cost of $55? i need the answer RN!!!!!!!
Answers
Answer: $88
x/55 is the same as 60%/1005 so 55 x 60 / 100 = 33 which is the mark up then add 55 and 33 to get the total price
Answer:
Price of shoes after markup is $88
Step-by-step explanation:
$55 + %60 markup or
55 x .60 = $33
55 + $33= $88
HELP!!!! THANK YOU ...........

Answers
Answer:
Using trigonometric ratio
sin(0)=opposite/hypotenise
sin(A)=BC/BA
sin(A)= 6/7
A=arcsin(6/7)
A=58.997°
A=59.00°
----------------------
Hope it helps...
Have a great day!!!
6. Inverse distance weighting: What is it for? Why is it better than just an average? (5)
Answers
Inverse distance weighting is a useful tool for estimating values at unsampled locations in geostatistics. Another advantage of inverse distance weighting is that it allows for the incorporation of multiple variables into the estimation process.
Inverse distance weighting is a method used in geostatistics to estimate values at unsampled locations based on values at surrounding sample locations. It works by assigning weights to the sample points based on their proximity to the unsampled point. The closer a sample point is to the unsampled point, the higher its weight. The weights are then used to calculate a weighted average of the sample values, which is used as the estimate for the unsampled location.
The benefit of inverse distance weighting over a simple average is that it takes into account the spatial variability of the data. A simple average treats all sample points equally, regardless of their distance from the unsampled point. This can lead to inaccurate estimates if there is a high degree of spatial variability in the data. In contrast, inverse distance weighting gives more weight to sample points that are closer to the unsampled point, which is likely to provide a more accurate estimate.
Another advantage of inverse distance weighting is that it allows for the incorporation of multiple variables into the estimation process. For example, if there are two variables of interest (e.g., temperature and precipitation), inverse distance weighting can be used to estimate values for both variables simultaneously. This is not possible with a simple average.
Overall, inverse distance weighting is a useful tool for estimating values at unsampled locations in geostatistics. Its ability to account for spatial variability and incorporate multiple variables makes it a powerful technique for analyzing spatial data.
for more questions on variables
https://brainly.com/question/29058061
#SPJ11
Can you solve 17+4x<9
Answers
Answer:
x<-2
Step-by-step explanation:
17+4x<9
4x<-8
x<-2
The solution is:
↬ x < -2Work/explanation:
Recall that the process for solving an inequality is the same as the process for solving an equation (a linear equation in one variable).
Make sure that all constants are on the right:
\(\bf{4x < 9-17}\)
\(\bf{4x < -8}\)
Divide each side by 4:
\(\bf{x < -2}\)
Hence, x < -2How to find the Length of a triangle

Answers
Answer:
10
Step-by-step explanation:
it us a right triangle so we can use the equation
a^2 + b^2 = c^2
6^2 + 8^2 = c^2
36 + 64 = c^2
100 = c^2
10 = c
on a given planet, the weight of an object varies directly with the mass of the object. suppose the am object whole mass is 5 kg weighs 15 N. Find the weight of an object while mass is 2 kg
Answers
The weight of an object with a mass of 2 kg would be 6 N on this planet, assuming the direct variation relationship holds.According to the given information, the weight of an object varies directly with its mass.
This implies that there is a constant of proportionality between weight and mass. Let's denote this constant as k.
From the given data, we have:
Mass = 5 kg
Weight = 15 N
Using the direct variation equation, we can write:
Weight = k * Mass
Substituting the given values, we have:
15 N = k * 5 kg
To find the value of k, we divide both sides of the equation by 5 kg:
k = 15 N / 5 kg = 3 N/kg
Now that we know the constant of proportionality, we can find the weight of an object with a mass of 2 kg:
Weight = k * Mass = 3 N/kg * 2 kg = 6 N.
For such more questions on Weight:
https://brainly.com/question/25973294
#SPJ11
what happens when the multiplicity of a real root is even
a. the graph crosses the y-axis
b. the graph crosses the x-axis
c. the graph is tangent to the y-axis
d. the graph is tangent to the x-axis
Answers
When the multiplicity of a real root is even, the graph of the function neither crosses nor is tangent to the x-axis. The correct answer is (c) the graph is tangent to the y-axis.
When a real root has an even multiplicity, it means that the corresponding factor appears multiple times in the factored form of the polynomial. In terms of the graph of the function, this means that the graph touches the x-axis at that root but does not cross it.
Since the graph touches the x-axis without crossing it, it remains on one side of the axis. This behavior indicates that the graph is tangent to the x-axis at the root with even multiplicity.
However, the graph can still intersect or cross the y-axis at a different point depending on other factors or terms in the polynomial. Therefore, option (a) "the graph crosses the y-axis" may or may not be true depending on the overall behavior of the function. The statement in option (b) "the graph crosses the x-axis" is incorrect for an even multiplicity root. Option (d) "the graph is tangent to the x-axis" is also incorrect for an even multiplicity root. Hence, option (c) "the graph is tangent to the y-axis" is the correct choice.
for such more question on tangent
https://brainly.com/question/31133853
#SPJ8
Find the Fourier transform of the given function f(x) = xe- ²x 0
Answers
To find the Fourier transform of the function\(f(x) = x * e^(-x^2),\) we can use the standard formula for the Fourier transform of a function g(x):
F(w) = ∫[from -∞ to ∞] g(x) * \(e^(-iwx) dx\)
In this case, g(x) = x * \(e^(-x^2)\)Plugging it into the Fourier transform formula, we get:
F(w) = ∫[from -∞ to ∞] \((x * e^(-x^2)) * e^(-iwx) dx\)
To evaluate this integral, we can use integration by parts. Let's define u = x and dv = \(e^(-x^2) * e^(-iwx)\) dx. Then, we can find du and v as follows:
du = dx
v = ∫ \(e^(-x^2) * e^(-iwx) dx\)
To evaluate v, we can recognize it as the Fourier transform of the Gaussian function. The Fourier transform of e^(-x^2) is given by:
F(w) = √π * \(e^(-w^2/4)\)
Now, applying integration by parts, we have:
∫(\(x * e^(-x^2)) * e^(-iwx) dx\)= uv - ∫v * du
= x * ∫ \(e^(-x^2) * e^(-iwx) dx\)- ∫ (∫ \(e^(-x^2) * e^(-iwx) dx) dx\)
Simplifying, we get:
∫(x * \(e^(-x^2)) * e^(-iwx) dx\)= x * (√π * \(e^(-w^2/4))\)- ∫ (√π * \(e^(-w^2/4)) dx\)
The second term on the right-hand side is simply √π * F(w), where F(w) is the Fourier transform of \(e^(-x^2)\) Therefore, we have:
(x * \(e^(-x^2))\)* \(e^(-iwx)\) dx = x * (√π *\(e^(-w^2/4)\)) - √π * F(w)
Hence, the Fourier transform of f(x) = x * \(e^(-x^2)\) is given by:
F(w) = x * (√π * \(e^(-w^2/4))\)- √π * F(w)
Please note that the Fourier transform of f(x) involves the Gaussian function, and it may not have a simple closed-form expression.
Learn more about Fourier transform here:
https://brainly.com/question/30398544
#SPJ11
I need help on this hurry please

Answers
Answer:
x=70
Step-by-step explanation:
sum is angles of a Pentagon=540°
x°+138°+2x°+80°+112°=540°
3x°+330°=540°
3x°=540°-330°
3x°=210°
3x°/3°=210°/3°
x=70
hope this is helpful
For the following right triangle, find the side length x.
X
9
12

Answers
Answer:
it's the square root of 63 and I'd assume rounding to the tenth but I dont know how ur teacher does it.
Step-by-step explanation:
find a calculator if u have one then solve for the square root of 63. this method is called the pythagorean theorem that i used
How do you solve this? Please help!

Answers
Answer:
b
Step-by-step explanation:
u can use the ration method
15:15+36
20:6x-7
then cross multiply
and x =12.5
Answer:
x = 12.5
Step-by-step explanation:
The large outer triangle and the small inner triangle are similar, thus the ratio of their corresponding sides are equal, that is
\(\frac{20}{6x-7}\) = \(\frac{15}{15+36}\) = \(\frac{15}{51}\) ( cross- multiply )
15(6x - 7) = 1020 ( divide both sides by 15 )
6x - 7 = 68 ( add 7 to both sides )
6x = 75 ( divide both sides by 6 )
x = 12.5
The quadratic functions f(x) and g(x) are described in the table. x f(x) g(x) −2 4 64 −1 1 49 0 0 36 1 1 25 2 4 16 3 9 9 4 16 4 5 25 1 6 36 0 In which direction and by how many units should f(x) be shifted to match g(x)? Left by 18 units Right by 18 units Left by 6 units Right by 6 units
Answers
Right by 6 units should f(x) be shifted to match g(x).
What is the quadratic functions?A quadratic function is a type of mathematical function that can be represented by an equation in the form of ax^2 + bx + c, where x is a variable, a, b, and c are coefficients, and a ≠ 0. Quadratic functions are commonly used in various fields including physics, engineering, and finance, to model various real-world phenomena.
Learn more about quadratic function in brainly.com/question/18958913
#SPJ1
I need help with this ( but I need to send another picture that has the answers )
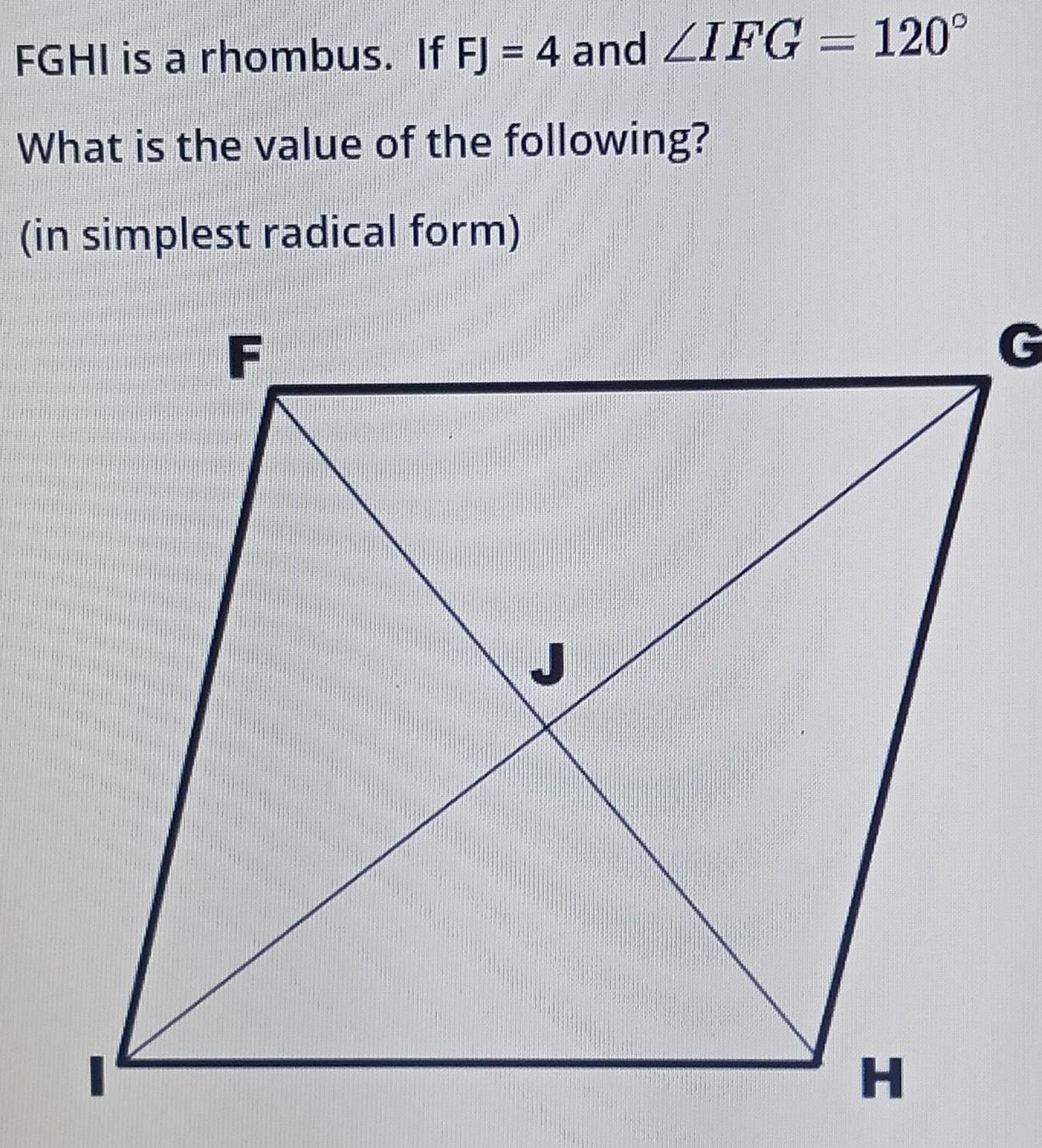

Answers
Step 1:
Draw the figure
The diagonals of a rhombus bisect each other,
therefore
FJ = JH
this implies that
JH = 4.
Opposite angles of a rhombus are equal, so
The diagonals of a rhombus bisect the interior angles.
Therefore,
\(\text{ angle JHG = }\frac{120^0}{2}=60^0\)The diagonals of a rhombus are perpendicular
\(\begin{gathered} Hence, \\ \cos 60^0=\frac{4}{GH} \\ \Rightarrow GH=\frac{4}{\cos60^0}=\frac{4}{\frac{1}{2}}=4\times2=8 \end{gathered}\)GH = 8 (b)
Also,
Using the Pythagorean rule,
\(\begin{gathered} JG^2+4^2=GH^2 \\ \Rightarrow JG^2+16=8^2 \\ \Rightarrow JG=\sqrt[]{64-16}=\sqrt[]{48}=4\sqrt[]{3}=6.928\text{ } \\ \text{right choice is C} \end{gathered}\)FH = FJ + JH
this implies that
FH = 4 + 4 = 8
FH = 8
right choice B
The diagonals of a rhombus bisect the interior angles.
therefore
\(\begin{gathered} angle\text{ JFG = }\frac{angle\text{ IFG}}{2}=\frac{120^0}{2}=60^0 \\ \text{ right choice is h} \end{gathered}\)Sum of the interior angles of a rhombus is 360degrees.
And opposite interior angles of a polygon are congruent.
Therefore
\(2(\text{angle FGH) +2(angle IFG) = 360degr}ees\)\(\begin{gathered} \text{this implies that} \\ 2(\text{angle FGH) = 360 - 2(angle IFG)} \\ \Rightarrow\text{angle FGH = 180 -angle IFG = 180 - 120= }60^0 \\ \text{ right choice is h} \end{gathered}\)\(\begin{gathered} \text{ but }FGJ\text{ = }\frac{FGH}{2}\text{ (diagonals bisect interior angles)} \\ \Rightarrow\text{FGJ =}\frac{60^0}{2}=30^0 \\ \text{right choice is j} \end{gathered}\)Also,
\(\begin{gathered} \(\begin{gathered} \text{JGH}=\text{ }\frac{FGH}{2}=\frac{60}{2}=30^0 \\ right\text{ choice is j} \end{gathered}\)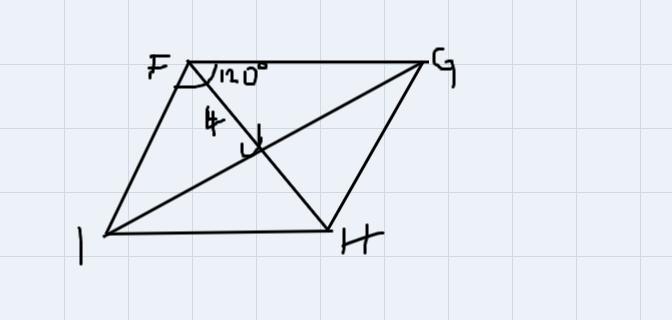
4 the time between arrivals of buses follows an exponential distribution, with a mean of 60 minutes. a what is the probability that exactly four buses will arrive during the next 2 hours? b that at least two buses will arrive during the next 2 hours? c that no buses will arrive during the next 2 hours? d a bus has just arrived. what is the probability that it will be between 30 and 90 minutes before the next bus arrives?
Answers
A)The probability of exactly four buses arriving in the next 2 hours is\($P(X=4)=e^{\wedge}(-2)\left(2^{\wedge} 4 / 4 !\right)=0.090$\) ≈ 0.090.
B) The probability of at least two buses arriving in the next 2 hours is =0.865
C) The probability of no buses arriving in the next 2 hours is =0.135
d) The probability that it will be between 30 and 90 minutes before the next bus arrives is ,0.185
a) Let \($X$\) be the number of buses that arrive in a 2-hour period. Since the time between arrivals of buses follows an exponential distribution with a mean of 60 minutes, the arrival rate λ is given by\($\lambda=1 / 60$\) 0 buses per minute.
Therefore, the number of buses that arrive in a 2-hour period is a Poisson distribution with parameter \(\mu=\lambda t=(1 / 60) \times 120=2$.\). Thus, X has a Poisson distribution with parameter μ = 2.
The probability of exactly four buses arriving in the next 2 hours is\($P(X=4)=e^{\wedge}(-2)\left(2^{\wedge} 4 / 4 !\right)=0.090$\) ≈ 0.090.
b) The probability of at least two buses arriving in the next 2 hours is
\($P(X \geq 2)=1-P(X=0)-P(X=1)=1-e^{\wedge}(-2)\left(2^{\wedge} 0 / 0 !\right)-e^{\wedge}(-2)\left(2^{\wedge} 1 / 1 !\right)=0.865$.\)
c) The probability of no buses arriving in the next 2 hours is
\(P(X=0)=$ $e^{\wedge}(-2)\left(2^{\wedge} 0 / 0 !\right)=0.135$\)
d) Let Y be the time between the first and second bus arrivals. Then Y follows an exponential distribution with a mean of 60 minutes. We want to find the probability that \($30 \leq Y \leq 90$\).
This is equivalent to finding \(P(Y \leq$ $90)-P(Y \leq 30)$,\), which is equal to F(90) - F(30), where F is the cumulative distribution function of the exponential distribution with \($\lambda=1 / 60$\)
Therefore, the probability that it will be between 30 and 90 minutes before the next bus arrives is\(F(90)-F(30)=\left(1-e^{\wedge}(-90 / 60)\right)-(1$ $\left.e^{\wedge}(-30 / 60)\right)=e^{\wedge}(-1.5)-e^{\wedge}(-0.5)=0.185$\)
Learn more about probability
https://brainly.com/question/30034780
#SPJ4
A boat takes 3.8 hours to travel 23.53 km down a river, then 6 hours to return. How fast is the river flowing
Answers
To determine how fast the river is flowing, we can use the concept of relative velocity.
This is because the boat is traveling both downstream and upstream, which means its speed is affected by the speed of the river.Let the speed of the boat be B and the speed of the river be R. Then, when traveling downstream, the boat's effective speed is:B + RAnd when traveling upstream, the boat's effective speed is:B - RWe know that the boat takes 3.8 hours to travel 23.53 km downstream.
This means that the boat's effective speed downstream is:23.53 km / 3.8 hours = 6.187 km/hour So we can write: B + R = 6.187 km/hour Similarly, we know that the boat takes 6 hours to travel the same distance upstream. This means that the boat's effective speed upstream is:23.53 km / 6 hours = 3.922 km/hour So we can write :B - R = 3.922 km/hour Now we have two equations with two unknowns (B and R). We can solve for R by adding the two equations.
To know more about velocity visit:
https://brainly.com/question/18084516
#SPJ11
Will give brainliest screenshot Will give brainliest screenshot Will give brainliest screenshot Will give brainliest screenshot attached

Answers
Answer:
one 5 and 2 ones hope this will help u
Answer:
One and five should be the answer.
Chloe ordered cards by the box from a company. She ordered 14 boxes, but 3 of the boxes were damaged when they arrived. The company charged her c dollars per box. The cost of the damaged boxes was subtracted from the total cost. Which expression represents the amount of money Chloe owes?
Answers
The expression which represents the amount of money Chloe owes is
amount = 14c - 3c. where 'c' is the cost per box.
What is a linear equation in one variable?
A linear equation is a one-variable equation of a straight line. The variable's only power is 1. Linear equations in one variable with the form an x + b = 0 are solved using basic algebraic operations.
Chloe ordered 14 boxes and per box 'c' dollars charged
Hence the total amount of money she has to pay is $14c
But 3 of the boxes are damaged so their price will be deducted from the total amount she was supposed to pay:
Now equation will become,
amount = 14c - 3c.
Hence, the expression which represents the amount of money Chloe owes is
amount = 14c - 3c. where 'c' is the cost per box.
To learn more about linear equations in one variable, visit:
https://brainly.com/question/85774
#SPJ4
What is the focus of the parabola y = 10x??
Answers
Answer:
The foci of y=10x would be y-x=1 I do exams and quizzes if your interested :)Can I have help on this?

Answers
Answer:
—4.5 and 0
Step-by-step explanation:
when x=—4.5 and x=0 y is included in the domain.
Graph the following rational functions by finding their
asymptotes & zeros.
x^3+3x-18 divided by 4x-4
Answers
The rational function given is f(x) = (x³+ 3x - 18) / (4x - 4). By analyzing its numerator and denominator, we can determine the asymptotes and zeros of the function.
To find the asymptotes of the given rational function, we examine the behavior of the function as x approaches positive or negative infinity. First, let's simplify the function by factoring the numerator and denominator. The numerator can be factored as (x - 2)(x² + 2x + 9), while the denominator is 4(x - 1).
The zeros of the function are the values of x for which the numerator equals zero. Setting (x - 2)(x² + 2x + 9) = 0, we find that x = 2 is a zero.
To determine the vertical asymptote, we set the denominator equal to zero and solve for x. Setting 4(x - 1) = 0 gives x = 1. Therefore, x = 1 is the vertical asymptote of the function.
With these findings, we can plot the graph of the rational function. The function has a vertical asymptote at x = 1, and it crosses the x-axis at x = 2, representing the zero of the function. The behavior of the function near the asymptote and zero can be further analyzed by examining the sign changes of the numerator and denominator in those regions.
Learn more about denominator here: https://brainly.com/question/15007690
#SPJ11
The complete question is:
Graph the rational function f(x) = (x³ + 3x - 18) / (4x - 4) by finding its asymptotes and zeros."
Gagu is paid £1200 per month.
He is going to get a 4% increase in the amount of money he is paid.
Work out how much Gagu will be paid per month after the increase.
Answers
Answer:
£1248
Step-by-step explanation:
1200x4%
=£48
1200+48=£1248
Gagu will be paid £1248 after the increase.
The amount Gagu paid per month after the 4% increment is £1248
What is the method to calculate x% increment?If there is x% increment in y then the increment will be (x/100)*y and the new amount after x% increment will be now y + (x*y)/100
Given that Gagu is paid £1200 per month. He is going to get a 4% increase in the amount of money he is paid.
Initial payment = £1200
4% increment = 4% of initial pay = 4(1200)/ 100 = £ 48
After increment new payment = Initial payment + 4% increment = 1200+48
= £1248
Therefore, The amount Gagu paid per month after the increase is £1248
Also, Learn more about the percentage increment from the link below:
https://brainly.com/question/27758670
#SPJ5