Find the equation of a line that passes through the points (6,7) and (8,3).
Leave your answer in the form
y = mx + c
Answers
Answer:
y=-2x+19
Step-by-step explanation:
For lines like these, the slope is always defined as "the change in y over the change in x" or, in equation form: m= \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\).
Now we have,
m= 3-7/8-6
m=-2. Since m=-2, the equation is y=-2x+b.
To find b, think about what your (x,y) points mean:
(6,7). When x of the line is 6, y of the line must be 7.
(8,3). When x of the line is 8, y of the line must be 3.
Substitute them to the equation y=-2x+b.
You can use either (x,y) point you want..the answer will be the same:
(6,7). y=mx+b or 7=-2 × 6+b, or solving for b: b=7-(-2)(6). b=19.
(8,3). y=mx+b or 3=-2 × 8+b, or solving for b: b=3-(-2)(8). b=19.
So, the equation of the line that passes through the points
(6,7) and (8,3) is y=-2x+19.
Related Questions
WHAT’S THE PERIMETER?????

Answers
Answer:
38
Step-by-step explanation:
10+10=20
4+4=8
3+3=6
4+6+8+20=38
The dimensions of a rectangular building
are 150 feet X 100 feet. Calculate the total
area of the building.
Answers
So the area is 15000 because 150 x 100 = 15000
please answer quickly

Answers
1a. 10. 24
1b. 125/243
2a. 0. 0048
2b. 32/3125
3a. 0. 64
3b. 0. 0031
4a. 2/5
4b. 48. 735
5a. 2. 36
5b. 1. 39
How to determine the values
1a. Given the values
(2/5)^2/(1/2)^6
Multiply both the numerator and denominator by the powers
⇒ \(\frac{\frac{4}{25} }{\frac{1}{64} }\)
To find the common ration, multiply thus;
⇒ \(\frac{4}{25}\) × \(\frac{64}{1}\)
⇒ \(\frac{256}{25}\)
= 10. 24
1b. (5/7)^2 × (5/7)^1
= \(\frac{25}{49}\) × \(\frac{5}{7}\)
= \(\frac{125}{343}\)
= 125/243
2a. 0. 6^1 × 0. 2^3
= 0. 6 × 0. 008
= 0. 0048
2b. (2/5)^3 × (2/5)^2
= \(\frac{8}{125}\) × \(\frac{4}{25}\)
= \(\frac{32}{3125}\)
= 32/ 3125
3a. 1^99 - 0. 6^2
= 1 - 0. 36
= 0. 64
3b. (0. 2 ) ^1 × (1/8)^2
= 0. 2 × 1/64
= 0. 2 × 0. 016
= 0. 0031
4a. (1/2)^2/ (5/8)^1
= \(\frac{\frac{1}{4} }{\frac{5}{8} }\)
Take the inverse of the denominator
= \(\frac{1}{4}\) × \(\frac{8}{5}\)
= 2/5
4b. 7^2 - 0. 5^3
= 49 - 0. 125
= 48. 875
5a. 3^1 - 0. 8 ^2
= 3 - 0. 64
= 2. 36
5b. 0. 7^2 + 0. 9^1
= 0. 49 + 0. 9
= 1. 39
Learn more about index notation here:
https://brainly.com/question/10339517
#SPJ1
Which construction is shown in the figure below?

Answers
Answer:
C
Step-by-step explanation:
Perpendicular bisector of line segment AB
does the equator cross the northen or southern part of south america south america is mostly located
Answers
Answer:
It crosses the northern part of south America! The equator is an imaginary line around the middle of a planet or other celestial body. It is halfway between the North Pole and the South Pole
Step-by-step explanation:
Answer:
Step-by-step explanation:
Please look up "equator" on the internet. You'll see that the equator passes through the South American country Ecuador. Ecuador is in the northern part of South America and the equator crosses mainly that part of the continent.
35 less than a number m is -72 help me please!

Answers
Answer:
m=-37
Step-by-step explanation:
m-35=-72
m=-37
(Please make me brainliest!)
Classify each as Polynomial or Not a Polynomial.
1.) 9x-^3 - 2y
2.) 2x^2 - 4√x
3.) 2x 2/3 - 4y
4.) 20x^2
5.) w/2 + 7
6.) 4y/2x
7.) -20x^2 + y
Answers
Not a Polynomial
Not a Polynomial
Polynomial
Not a Polynomial
Not a Polynomial
Polynomial
I need help with this 1

Answers
a). Exact volume of cylinder is equal to 4224 cm³
b). Exact volume of the cone is equal to 1408 cm³
c). The approximate volume of the cone is equal to 1406.7 cm³
How to evaluate for the volume of the cylinder and cone
a). volume of the cylinder = 22/7 × (8cm)² × 21cm
volume of the cylinder = 22 × 64 cm² × 3 cm
exact volume of the cylinder = 4224 cm³
b). volume of the cone = 1/3 × 22/7 × (8cm)² × 21cm
exact volume of the cone = 22 × 64 cm² × 1 cm
exact volume of the cone = 1408 cm³
c). using the approximate vale of π = 3.14
approximate volume of the cone = 1/3 × 3.14 × (8cm)² × 21cm
approximate volume of the cone = 3.14 × 64 cm² × 7 cm
approximate volume of the cone = 1406.7 cm³
Therefore, the Exact volume of the cylinder and cone are 4224 cm³ and 1408 cm³ respectively. While the approximate volume of the cone is equal to 1406.7 cm³
Read more about volume here:https://brainly.com/question/24259805
#SPJ1
Approximate the value of each irrational expression. Use 22/7 as a rational approximation for pi.
2pi
5pi + 1
Pi to the second power
Answers
Answer:
pi=22/7
2pi=44/7
5pi+1=110/7+1=117/7
pi to the second power=22/7 times 22/7=484/49
Hope this helps, but I don't know.
Answer:
hi
Step-by-step explanation:
When looking at a graph, explain how you would know two variables were not proportional.
Answers
Answer:
a straight line that does not go through the origin.
Which side lengths do not form a right triangle?
a. 5, 12, 13
b. 10, 24, 28
c. 15, 36, 39
d. 50, 120, 130
Answers
Answer:
B.
Step-by-step explanation:
28 is not a multiple of 13.
Find the minimum distance from the point (8, 0, 9) to the plane x - y + z = 4. (Hint: To simplify the computations, minimize the square of the distance.)
Answers
Given:A point is (8, 0, 9) and Plane equation is x - y + z = 4. The minimum distance from the point (8, 0, 9) to the plane x - y + z = 4.We know that the shortest distance from a point to a plane is along the perpendicular.
Let the point P(8, 0, 9) and the plane is x - y + z = 4. Then a normal vector n to the plane is given by the coefficients of x, y and z of the plane equation, i.e., n = (1, -1, 1).Therefore, the equation of the plane can be written as (r - a).n = 4, where r = (x, y, z) and a = (0, 0, 4) is any point on the plane.Substituting the values, we have (r - a).n
\(= ((x-8), y, (z-9)).(1, -1, 1) = (x-8) - y + (z-9) = 4So, (x-8) - y + (z-9) = 4x - y + z - 21 = 0\)
Now, the distance from the point P to the plane can be given by:Distance d = |(P - a).n| / |n|where |n| = \(√(1^2 + (-1)^2 + 1^2) = √3Then, d = |(8, 0, 9) - (0, 0, 4)).(1, -1, 1)| / √3= |(8, 0, 5)).(1, -1, 1)| / √3= |8(1) + 0(-1) + 5(1)| / √3= 13 /\)√3 Since the denominator √3 is less than 2, then the numerator is greater than 13*2=26. This means that d > 26. Hence the minimum distance from the point (8, 0, 9) to the plane x - y + z = 4 is greater than 26 or more than 100.
To know more about minimum visit:
https://brainly.com/question/21426575
#SPJ11
3) [4 pts] Calculate the pair-wise distance matrix (total number of changes) and the Neighbor-joining tree revising the matrix every time. [1 pt] How does this tree compare with the most parsimonious one? Evolution; BIOL:3172 Phylogeny Exercise. Name: Section: 3) [4 pts] Calculate the pair-wise distance matrix (total number of changes) and the Neighbor-Joining tree revising the matrix every time. [1 pt] How does this tree compare with the most parsimonious one?
Answers
The Neighbor-Joining tree generated using the pair-wise distance matrix may not be the most parsimonious one.
Let's start by calculating the pair-wise distance matrix, which represents the total number of changes between each pair of sequences. Each change can be a substitution, insertion, or deletion. Once we have the distance matrix, we can construct the Neighbor-Joining tree by iteratively joining the closest sequences.
The Neighbor-Joining tree is a commonly used method to infer phylogenetic relationships. However, it is important to note that it may not always represent the most parsimonious tree. The parsimony principle assumes that the tree with the fewest number of changes is the most likely tree. In other words, it seeks to minimize the total number of evolutionary changes required to explain the observed sequences.
The Neighbor-Joining tree, on the other hand, is based on the concept of minimizing the total branch length of the tree, which may not necessarily correspond to the fewest number of changes. Therefore, the Neighbor-Joining tree may differ from the most parsimonious tree in terms of the sequence of branching events or the number of changes required. It is always advisable to consider multiple methods and evaluate the support for different tree topologies to obtain a comprehensive understanding of the phylogenetic relationships.
Learn more about matrix here: brainly.com/question/28180105
#SPJ11
If S={a,b,c} with P(a)=2P(b)=3P(c), find P(a). 9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a). 10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a). 11. If E and F are two disjoint events in S with P(E)= 0.2 and P(F)=0.4, find P(E∪F),P(E
c
), and P(E∩F). 12. Why is it not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7? 13. If E and F are two disjoint events in S with P(E)= 0.4 and P(F)=0.3, find P(E∪F),P(F
c
),P(E∩F), P((E∪F)
c
), and P((E∩F)
c
). 14. Why is it not possible for S={a,b,c} with P(a)= 0.3,P(b)=0.4, and P(c)=0.5 ?
Answers
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a).
Since P(a), P(b), and P(c) are equal, we can let P(a) = P(b) = P(c) = x.
Then, we know that P(d) = P(e) = P(f) = 0.1.
The total probability of the sample space S is equal to 1. So, we can write the equation:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
Substituting the given values, we get:
3x + 0.1 + 0.1 + 0.1 = 1
3x + 0.3 = 1
3x = 1 - 0.3
3x = 0.7
Dividing both sides by 3, we find:
x = 0.7/3
So, P(a) = 0.233.
10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a).
Let P(a) = P(b) = P(c) = x. And let P(d) = P(e) = P(f) = y.
We also know that P(d) = 2P(a).
Using the equation for the total probability:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
We can substitute the given values:
3x + 3y = 1
We also know that P(d) = 2P(a):
y = 2x
Substituting this into the previous equation:
3x + 3(2x) = 1
3x + 6x = 1
9x = 1
Dividing both sides by 9, we find:
x = 1/9
So, P(a) = P(b) = P(c) = 1/9.
11. If E and F are two disjoint events in S with P(E)=0.2 and P(F)=0.4, find P(E∪F), P(Ec), and P(E∩F).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.2 + 0.4 = 0.6
The complement of E, Ec, is the event that consists of all outcomes in S that are not in E.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Ec) = 1 - P(E) = 1 - 0.2 = 0.8
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
12. It is not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7 because the sum of their probabilities would exceed 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for two events with probabilities that add up to more than 1 to be disjoint.
13. If E and F are two disjoint events in S with P(E)=0.4 and P(F)=0.3, find P(E∪F), P(Fc), P(E∩F), P((E∪F)c), and P((E∩F)c).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.4 + 0.3 = 0.7
The complement of F, Fc, is the event that consists of all outcomes in S that are not in F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Fc) = 1 - P(F)
= 1 - 0.3
= 0.7
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
The complement of the union of two events, (E∪F)c, is the event that consists of all outcomes in S that are not in the union of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∪F)c) = 1 - P(E∪F) = 1 - 0.7 = 0.3
The complement of the intersection of two events, (E∩F)c, is the event that consists of all outcomes in S that are not in the intersection of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∩F)c) = 1 - P(E∩F) = 1 - 0 = 1
14. It is not possible for S={a,b,c} with P(a)=0.3, P(b)=0.4, and P(c)=0.5 because the sum of their probabilities exceeds 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
someone please help im gonna fail

Answers
Answer:
The order will be 2, 3, 4 & 1
Answer:
Juana lee Ann Jackson ryne
Step-by-step explanation:
can i have brainly
HELP UR WORK FOR THIS and please explain with it thank you

Answers
Divide the amount of money she spent all together by the price of what it costs to get a refill which is $1.25
Jose can use the rule m(x)=10+3x to find m(x) , the amount of money he will have after a week of doing x additional hours of chores. Evaluate m(20), What does this mean?
Answers
Answer:
70
Step-by-step explanation:
Given:
m(x) = 10 + 3x
where,
m(x) = the amount of money he will have after a week of doing x additional hours of chores
x = additional hours of chores
Evaluate m(20), What does this mean?
m(x) = 10 + 3x
m(20) = 10 + 3(20)
= 10 + 60
= 70
m(20) = 70
m(20) means additional hours of chores is 20
porfavor ayudenme con esta radicacion no la entiendo√81 ∙ 49
Answers
Answer:
441
Step-by-step explanation:
sqrt81=9
9 x 49=441
Answer:
441
Step-by-step explanation:
√ 9 ^2 ⋅ 49
9 ⋅ 49 = 441
HEEEEEEEELLLLLLLLLLPPPPPPPPP!!!!!!!!!
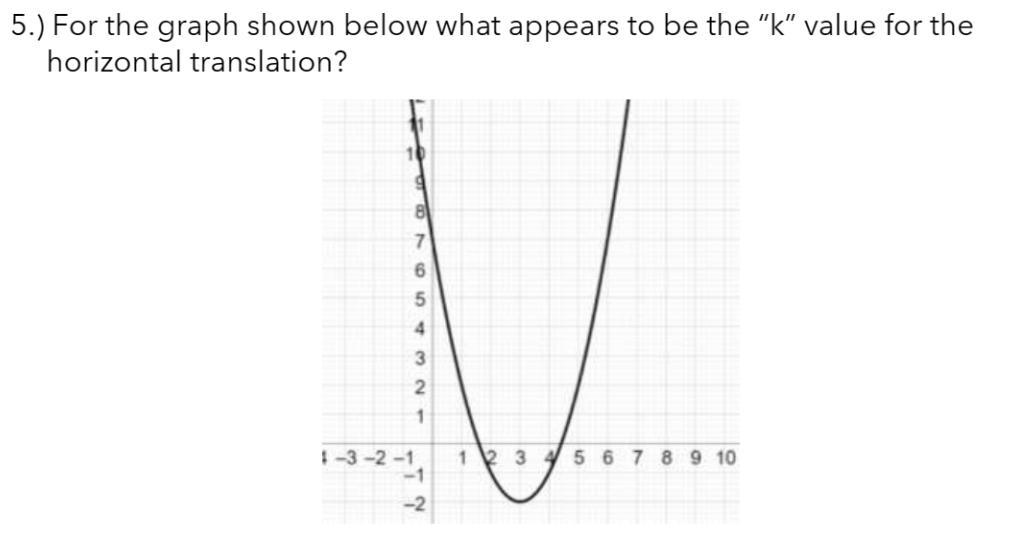
Answers
Answer:
The horizontal translation of the function is 3 units to the right (from the parent function). Therefore, we subtract 3 from the x-value of the function.
The equation of the graphed function in vertex form is:
\(\boxed{y = (x - 3)^2- 2}\)
Step-by-step explanation:
The given graph shows a parabola that opens upwards.
Therefore, the equation for this function is a quadratic equation with a positive leading coefficient.
The vertex of a parabola is the minimum point of a parabola that opens upwards, or the maximum point of a parabola that opens downwards.
From inspection of the given graph, the vertex of the function is (3, -2).
The parent function of a parabola that opens upwards is y = x². This has a vertex at (0, 0).
Therefore, given the vertex of the given function is (3, -2), the parent function has been translated 3 units right and 2 units down.
For a horizontal translation to the right, we subtract the number of units from the x-value of the function.
For a vertical translation down, we subtract the number of units from the function.
Therefore, a translation of 3 units right and 2 units down from the parent function y = x² is:
\(\boxed{y = (x - 3)^2- 2}\)
This function is written in vertex form.
To write the equation in standard form, expand the brackets and simplify:
\(\implies y=(x-3)(x-3)-2\)
\(\implies y=x^2-3x-3x+9-2\)
\(\implies y=x^2-6x+7\)
\(\hrulefill\)
Additional comments
The vertex form of a quadratic equation is y = a(x - h)² + k, where (h, k) is the vertex. Therefore, the "k" value refers to the y-value, which is the vertical translation from the parent function.
As your question refers to the "k" value for the horizontal translation, we assume that it is not referring to the k-value of the vertex form.
Which symbol creates a true sentence when x = 6?
12 ÷ x + 2x ____ 12 ÷ (x + 2x)
Responses
=
>
Answers
A symbol that creates a true sentence for x = 6 is '>' i.e.,
12 ÷ x + 2x > 1 2 ÷ (x + 2x)
In this question, we have been given a statement 12 ÷ x + 2x ____ 12 ÷ (x + 2x)
We need to select a correct symbol that would create a true sentence when x = 6.
Consider an expression 12 ÷ x + 2x for x = 6.
= 12 ÷ 6 + 2(6)
= 2 + 12
= 14 ...................(1)
Consider an expression 12 ÷ (x + 2x) for x = 6
= 12 ÷ (6 + 2(6))
= 12 ÷ (6 + 12)
= 12 ÷ 18
= 0.67 ...................(2)
From (1) and (2),
14 > 0.67
Therefore, a symbol that creates a true sentence for x = 6 is '>'
i.e., 12 ÷ x + 2x > 1 2 ÷ (x + 2x)
Learn more about an expression here:
https://brainly.com/question/1859113
#SPJ1
Halp. me. e-x-p-l-a-i-n how you got your answer

Answers
The linear equation that passes through the anchor points (-3, -38) and (8, 61) is:
y = 9*x - 11
How to find the equation of the line?
The general linear equation is written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
We know that for a line that passes through two points (x₁, y₁) and (x₂, y₂) can be written as:
a = (y₂ - y₁)/(x₂ - x₁)
Now, in this case we know that our line passes through the points (-3, -38) and (8, 61), then the slope will be:
a = (61 + 38)/(8 + 3) = 9
Replacing that we get:
y = 9*x + b
Now, using one of the points we can find the y-intercept, I will use (8, 61), replacing the values we get:
61 = 9*8 + b
61 = 72 + b
61 - 72 = b
-11 = b
The linear equation is:
y = 9*x - 11
Learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
Find the value of x.
44.8
37.5
17.5
22.0

Answers
Answer:
x = 17.5
Step-by-step explanation:
\( \frac{16}{10} = \frac{28}{x} \) (angle bisector theorem)
Cross multiply
16 × x = 28 × 10
16x = 280
Divide both sides by 16
x = 280/16
x = 17.5
A high school baseball player has a 0.267 batting average. In one game, he gets 8 at bats. What is the probability he will get at least 6 hits in the game
Answers
The probability that the high school baseball player will get at least 6 hits in the game is approximately 0.377, or 37.7%.
To calculate the probability that the high school baseball player will get at least 6 hits in the game, we can use the binomial distribution. The binomial distribution is appropriate here because each at-bat is independent, and there are only two outcomes (hit or no hit) for each at-bat.
The probability of getting a hit in a single at-bat is given by the batting average, which is 0.267. Therefore, the probability of not getting a hit in a single at-bat is 1 - 0.267 = 0.733.
We want to calculate the probability of getting at least 6 hits in 8 at-bats. This includes the probabilities of getting exactly 6, 7, and 8 hits. We can calculate these probabilities separately and sum them up.
To calculate the probability that the high school baseball player will get at least 6 hits in the game, let's use the binomial distribution.
P(X >= 6) = P(X = 6) + P(X = 7) + P(X = 8)
Where:
P(X = k) is the probability of getting exactly k hits
P(X >= 6) is the probability of getting at least 6 hits
X is the random variable representing the number of hits in the game
k is the number of hits
Let's calculate each probability:
\(P(X = 6) = C(8, 6) * (0.267^6) * (0.733^2)\\ = 28 * (0.267^6) * (0.733^2)\\ = 0.242\)
\(P(X = 7) = C(8, 7) * (0.267^7) * (0.733^1)\\ = 8 * (0.267^7) * (0.733^1)\\ = 0.123\)
\(P(X = 8) = C(8, 8) * (0.267^8) * (0.733^0)\\ = 1 * (0.267^8) * (0.733^0)\\ = 0.012\)
Now, let's sum up these probabilities:
P(X >= 6) = P(X = 6) + P(X = 7) + P(X = 8)
= 0.242 + 0.123 + 0.012
= 0.377
Therefore, the probability that the high school baseball player will get at least 6 hits in the game is approximately 0.377, or 37.7%.
Learn more about Probability at:
https://brainly.com/question/25839839
#SPJ4
How do you solve a differential equation with exponential equations?
Answers
To solve a differential equation with exponential equations, start by isolating the dependent variable and any coefficients that may exist on either side of the equation. Next, take the natural logarithm of both sides of the equation and use the properties of logarithms to simplify the equation. Solve for the dependent variable. Finally, take the exponential of both sides of the equation and simplify it to get the solution.
For example, consider the differential equation dy/dx = 2y.
Isolate the dependent variable to get y = dx/2.
Then, take the natural logarithm of both sides to get ln(y) = ln(dx/2).
Use the property ln(a/b) = ln(a) - ln(b) to get ln(y) = ln(dx) - ln(2).
Solve for ln(y) to get ln(y) = ln(dx) - ln(2).
Then, take the exponential of both sides to get \(y = e^{ln(dx) - ln(2)}\) and simplify to get the solution \(y = (dx/2) e^{ln(dx)}\).
Know more about Logarithm here :
https://brainly.com/question/30976287
#SPJ11
Please answer correctly !!!!! Will mark brainliest !!!!!!!!!!!

Answers
Answer:
9 degrees Celsius
Step-by-step explanation:
I graphed the function on the graph below to find the maximum of the parabola. The maximum is at (9,200), which means at 9 degrees Celsius, there are 200,000 fish.

The temperature at which there will be maximum number of fishes is given by the point (9, 200), is it is 9 degrees.
Given data:
To find the temperature that will result in the maximum number of fish, determine the x-value (temperature) at the vertex of the quadratic function.
The given function is P(x) = -2(x - 9)² + 200, where P(x) represents the fish population in thousands and x represents the water's temperature.
The general form of a quadratic function is y = a(x - h)² + k, where (h, k) represents the vertex of the parabola.
The vertex form of the function is P(x) = -2(x - 9)² + 200.
Comparing this to the general form, the vertex of the parabola is at the point (9, 200).
Hence, the temperature that will result in the maximum number of fish is 9 degrees (the x-value of the vertex).
To learn more about parabola click :
https://brainly.com/question/24042022
#SPJ2
How do I solve 8k-9(4K+4)
Answers
Answer:
-28k - 36
Step-by-step explanation:
8k - 9(4k+4)
distribute -9 into the ( )
8k - 36k -36
combine 8k and - 36k to get - 28k
-28k-36
hope this helps!!!
Genevieve is buying snacks at the concession stand.she bought 3 hamburgers and 2 order of fries.the fries cost 2.50$.she spent a total of 14.00 how much did a hamburger cost
Answers
Answer:
3$
Step-by-step explanation:
3h (hamburgers) + 2f (fries) = 14$
3h+2(2.5)=14
3h+5=14
3h=9
h=3
Find the solution to the following.Make sure you simplify. 1/2 + 2/5 , 1/2 - 2/5 , 1/2 ÷ 2/5 ,1/2 • 2/5
Answers
Answer:
9/10,1/10,1 1/4, and 1/5
If you know the rules of adding, subtracting, dividing, and multiplying decimals, you know what to do. If not, then I can show you if you'd like
A bee flies at 6 feet per second directly to a flowerbed from its hive. The bee stays at the flowerbed for 18 minutes, and then flies directly back to the hive at 4 feet per
second. It is away from the hive for a total of 20 minutes
a. What equation can you use to find the distance of the flowerbed from the hive?
b. How far is the flowerbed from the hive
Answers
Answer: T=x+y
T=600 ft
Step-by-step explanation:
T=Total distance
a. x=distance in feet/second traveled from hive to flowerbed
y=distance in feet/second traveled to hive
20*60=1200 seconds
18*60=1080 seconds
T=x+y ==> equation
b. x/6=y/4=60 seconds ==> 1 min
x/6=60
x=360 feet
y/4=60
y=240 feet
x+y=
360+240=600 ft
If 1 3/4 cups of cheese are needed for four
servings, how many cups of cheese are
needed for 10 servings?
Answers
Answer:
17 1/2
Step-by-step explanation:
make the 1 3/4 into completely quarters which would be 7/4 and then multiply by 10
\( \frac{7}{4} \times \frac{10}{1} \)
then multiply from across and simplify