Find the directional derivative of f(x,y,z)=z3−x2y
at the point (-3,-2,-4) in the direction of the vector v=⟨3,3,−5⟩
Answers
The directional derivative of the function f(x, y, z) at the point (-3, -2, -4) in the direction of the vector v = ⟨3, 3, -5⟩ is -36.
Given: A function f(x, y, z) = z³ - x²y and a vector v = ⟨3, 3, -5⟩.
The point at which the directional derivative needs to be calculated is (-3, -2, -4).
Required: Directional derivative of the function f(x, y, z) at the point (-3, -2, -4) in the direction of the vector v = ⟨3, 3, -5⟩.
Formula used:The directional derivative of a function f(x, y, z) at a point P(x₀, y₀, z₀) in the direction of the vector v = ⟨a, b, c⟩ is given by the formula:
Dᵥf(x₀, y₀, z₀) = ∇f(x₀, y₀, z₀)·v = afx + bfy + cfz.
where ∇f(x₀, y₀, z₀) is the gradient of the function f(x, y, z) at the point P(x₀, y₀, z₀).
Calculation:
Given function is f(x, y, z) = z³ - x²y
∴ fx = -2xy and fz = 3z²
∴ fy = -x² and
∇f(x, y, z) = ⟨-2xy, -x², 3z²⟩
At the point (-3, -2, -4), we have
∇f(-3, -2, -4) = ⟨12, -4, 48⟩
and v = ⟨3, 3, -5⟩.
∴ Dᵥf(-3, -2, -4) = ∇f(-3, -2, -4)·v
= (12)(3) + (-4)(3) + (48)(-5)
=-36
Hence, the directional derivative of the function f(x, y, z) at the point (-3, -2, -4) in the direction of the vector v = ⟨3, 3, -5⟩ is -36.
To know more about vector visit:
https://brainly.com/question/24256726
#SPJ11
Related Questions
Consider the following.
y = 2xe−x, y = 0, x = 2; about the y-axis
Set up an integral for the volume V of the solid obtained by rotating the region bounded by the given curve about the specified axis.
Answers
Volume of the solid obtained by rotating the region bounded by curve y = 2xe⁻ˣ, y = 0, x = 2 about y-axis is \($$V = \int_0^2 2\pi y \sqrt{2}\ dy$$\)
To apply the cylindrical shell method, we have to consider vertical cylinders, whose height is same as the height of the curve and whose radius is the perpendicular distance from the axis of rotation to a point on the curve.
Volume of each cylinder is given by formula:
\($$V_\text{cylinder} = 2\pi rh\Delta x$$\) where h the is height of cylinder and r is radius. To obtain the volume of the solid, we add the volume of all the cylindrical shells.
To set up the integral, we have to find the expression for r and h and since we are rotating about y-axis, we need to express x in terms of y. From the equation,
y = 2xe⁻ˣ, we have:\($$x = \frac{y}{2e^{-x}}$$\)
We can use the property that \(e^(-x)\) is the reciprocal of \(e^x\) to write:
\($${e^x} = \frac{1}{e^{-x}}$$\)
Substituting, we get: \($$x = \frac{y}{2}e^x$$\)
Next, we find the limits of integration. The curve y = 2xe⁻ˣ, y = 0, x = 2 encloses a region in the first quadrant.
To find the limits of integration, we need to solve for the two points of intersection of the curve with the axis of rotation. We get:
\($y = 2xe^{-x}\)
\(= 0$$x\)
\(= 0$ or $x\)
\(= 2$\)
Hence, we integrate from 0 to 2.To express r and h in terms of y, we draw a diagram of a typical cylindrical shell and the region being rotated:
From the diagram, we see that:
\($r = x\)
\(= \frac{y}{2}e^x\)
\(= \frac{y}{2}e^{\ln 2y}\)
\(= y \sqrt{2}$$h\)
=\(\Delta x\)
= \(dx$\)
Thus, the volume of each cylindrical shell is:
\($$dV = 2\pi rh\ dx\)
\(= 2\pi y \sqrt{2}\ dx$$\)
The total volume is obtained by integrating from 0 to 2: \($$V = \int_0^2 2\pi y \sqrt{2}\ dy$$\)
Volume of the solid obtained by rotating the region bounded by curve y = 2xe⁻ˣ, y = 0, x = 2 about y-axis.
To know more about volume of the solid, refer
https://brainly.com/question/20284914
#SPJ11
Geometry: complete this proof of theorem 14, ASAP!
(Theorem 14: if a transversal intersects two lines so that corresponding angles are congruent, then the lines are parallel.)

Answers
Answer:
1. Transversal y intersects lines m and n; <1 ~= <2 (Given)
2. <1 ~= <3 (Vertical Angles Theorem)
3. <2 ~= <3 (Transitive Property of Congruence)
4. m || n (Converse of Alternate Interior Angles Theorem)
Find the monthly house payments necessary to amortize 7.2% loan of 256.400 $ over 30 years.The payment size is $Round to the nearest cent
Answers
To amortize a loan of $256,400 with an interest rate of 7.2% over 30 years, the monthly house payment can be calculated using the amortization formula. The payment size is $1,758.70 (rounded to the nearest cent).
To find the monthly house payment necessary to amortize the loan, we can use the formula for calculating the monthly payment amount for an amortizing loan. The formula is given by:
Payment = (Loan Amount * Monthly Interest Rate) / (1 - (1 + Monthly Interest Rate)^(-Number of Payments))
First, we need to convert the annual interest rate to a monthly interest rate. The monthly interest rate can be calculated by dividing the annual interest rate by 12 and converting it to a decimal. In this case, the monthly interest rate is 7.2% / 12 = 0.006.
Next, we substitute the values into the formula. The loan amount is $256,400, the monthly interest rate is 0.006, and the number of payments is 30 years * 12 months = 360 months.
Plugging in these values into the formula, we have:
Payment = (256,400 * 0.006) / (1 - (1 + 0.006)^(-360))
Calculating this expression, we find that the monthly house payment necessary to amortize the loan is approximately $1,758.70 when rounded to the nearest cent.
Learn more about amortization formula here:
https://brainly.com/question/16554334
#SPJ11
The six measurements that follow are furnace temperatures recorded on successive batches in a semiconductor manufacturing process (units are degrees Fahrenheit): 953, 950, 948, 955, 951, 955. (a) Calculate the sample mean, sample variance, and sample standard deviation. (b) Find the range and median. How much could the largest temperature measurement increase without changing the median value
Answers
\(\textbf{(a) Sample Mean, Sample Variance, and Sample Standard Deviation:}\)
To calculate the sample mean, sample variance, and sample standard deviation, we'll use the following formulas:
Sample Mean:
\(\[\bar{x} = \frac{{\sum_{i=1}^{n} x_i}}{n}\]\)
Sample Variance:
\(\[s^2 = \frac{{\sum_{i=1}^{n} (x_i - \bar{x})^2}}{n-1}\]\)
Sample Standard Deviation:
\(\[s = \sqrt{s^2}\]\)
where:
\(\(\bar{x}\) = sample mean,\\\(x_i\) = individual temperature measurements,\\\(n\) = number of measurements,\\\(s^2\) = sample variance,\\\(s\) = sample standard deviation.\)
Given the temperature measurements: 953, 950, 948, 955, 951, 955, we can plug these values into the formulas to calculate the desired statistics.
Sample Mean:
\(\[\bar{x} = \frac{953 + 950 + 948 + 955 + 951 + 955}{6} = 952\]\)
Sample Variance:
\(\[s^2 = \frac{(953-952)^2 + (950-952)^2 + (948-952)^2 + (955-952)^2 + (951-952)^2 + (955-952)^2}{6-1} = 6\]\)
Sample Standard Deviation:
\(\[s = \sqrt{6} \\\\\approx 2.449\)
Therefore, the sample mean is 952, the sample variance is 6, and the sample standard deviation is approximately 2.449.
\(\textbf{(b) Range and Median:}\)
The range is the difference between the largest and smallest values in the data set. The median is the middle value when the data set is arranged in ascending order.
Range:
The largest temperature measurement is 955, and the smallest is 948. Therefore, the range is \(\(955 - 948 = 7\)\).
Median:
Arranging the data set in ascending order: 948, 950, 951, 953, 955, 955. The middle value is the average of the two middle numbers, which are 951 and 953. Thus, the median is \(\(\frac{(951 + 953)}{2}= 952\)\).
The largest temperature measurement could increase without changing the median value by any amount less than or equal to half the range (\(\frac{7}{2}\) = 3.5 degrees Fahrenheit). As long as the largest temperature remains below 955 + 3.5, the median will remain unchanged.
To know more about Average visit-
brainly.com/question/18029149
#SPJ11
Can anybody give me the answer for this.. I have no idea how to do it and it would really improve my grade

Answers
Step-by-step explanation:
The question is to combine the equations, so we should add them.
- 2x -4y = -26
+ - 3x -3y = - 12
(same signs add, different signs subtract)
-5x -7y = -38
(in the question there are two boxes at the side of the eqaution you should put (+)sign there as youre adding them)
If this question was supposed to be subtracted it would give a while different ans)
What is the length of AB

Answers
Answer:
12.64
Step-by-step explanation:
cos 53 = Adjacent side/Hypotenuse
cos 53 = Adjacent side/21
21 * cos 53 = (Adjacent side/21) * 21
21 cos 53 = Adjacent side
Adjacent side (AB) ≈ 12.64
can you guys help me? thank you
Write 4.9 x 10^9 m in standard notation.
Write 3.2 x 10^-5 in standard notation.
Answers
Answer:
4.9 x 10^9 = 4,900,000,000
3.2 x 10^-5 = 0.000032
Step-by-step explanation:
4.9 x 10^9 = 4,900,000,000: note the 9 places after the 4.
10^9 = 1,000,000,000; after substituting,
4.9 x 1,000,000,000 = 4,900,000,000
10^-5 = 0.00001
3.2 x 0.00001 = 0.000032
Nina can stitch 2/3 of dress in 4 hours. If represents the number of dresses and the represents the number of hours, which equation represents this proportional relationship?
Answers
Answer:
d :4h
Step-by-step explanation:
hope this helps (;
Theresa and Raul purchased a house 10 years ago for $200,000. They made a down payment of 20% of the purchase price and secured a 30 year conventional home mortgage at 6% per year compounded monthly on the unpaid balance. The house is now worth $380,000. How much equity do Teresa and Raul have in their house now (after making 120 monthly payments)? Please show all work.
2. Emon is securing a 7-year balloon mortgage for $280,000 to finance the purchase of his first home. The monthly payments are based on a 30 year amortization. If the interest rate is 2.9% per year compounded monthly, what will be his balloon payment at the end of the 7 years? Please show all work.
Answers
Theresa and Raul have approximately $264,875.60 in equity in their house after making 120 monthly payments. Emon’s balloon payment at the end of 7 years is approximately $190,347.68.
Let’s calculate the equity that Theresa and Raul have in their house now:
1. Initial purchase price: $200,000
Down payment: 20% of $200,000 = $40,000
Loan amount: $200,000 - $40,000 = $160,000
2. Monthly interest rate: 6% / 12 months = 0.06 / 12 = 0.005
Number of monthly payments: 30 years * 12 months = 360 months
To calculate the monthly payment, we can use the formula for a fixed-rate mortgage:
Monthly payment = P * r * (1 + r)^n / ((1 + r)^n – 1)
Where:
P = Loan amount = $160,000
R = Monthly interest rate = 0.005
N = Number of monthly payments = 360
Using this formula, we can calculate the monthly payment:
Monthly payment = $160,000 * 0.005 * (1 + 0.005)^360 / ((1 + 0.005)^360 – 1)
≈ $959.37
Now, let’s calculate the total amount paid over the 120 monthly payments:
Total amount paid = Monthly payment * Number of monthly payments
= $959.37 * 120
= $115,124.40
Finally, to calculate the equity, we subtract the total amount paid from the current house value:
Equity = Current house value – Total amount paid
= $380,000 - $115,124.40
= $264,875.60
Therefore, Theresa and Raul have approximately $264,875.60 in equity in their house now.
Now let’s calculate Emon’s balloon payment at the end of 7 years:
1. Loan amount: $280,000
2. Monthly interest rate: 2.9% / 12 months = 0.029 / 12 = 0.00242
Number of monthly payments: 7 years * 12 months = 84 months
To calculate the monthly payment, we can use the same formula as before:
Monthly payment = P * r * (1 + r)^n / ((1 + r)^n – 1)
Where:
P = Loan amount = $280,000
R = Monthly interest rate = 0.00242
N = Number of monthly payments = 360
Using this formula, we can calculate the monthly payment:
Monthly payment = $280,000 * 0.00242 * (1 + 0.00242)^84 / ((1 + 0.00242)^84 – 1)
≈ $1,125.32
Since the monthly payments are based on a 30-year amortization, at the end of 7 years, there will still be a remaining balance on the loan.
Remaining balance = Loan amount – (Monthly payment * Number of monthly payments)
= $280,000 – ($1,125.32 * 84)
≈ $190,347.68
Therefore, Emon’s balloon payment at the end of 7 years would be approximately $190,347.68.
Learn more about Loans here: brainly.com/question/29045243
SPJ11
Nandini makes 'halwa' one evening and divides it into four equal portions for her family of four. However, just as they are about to eat it, an unexpected guest arrives and Nandini has to now re-divide the halwa into five equal portions. By what percentage has each family member's share reduced due to this?
Answers
Answer:
5%
Step-by-step explanation:
We know that when there are four people, then each person gets 25% of the halwa. However, when the fifth person comes, they have everyone including the guest get 20% of the halwa. In this way, the original four people are losing 5% of their halwa in order for the fifth person to get his piece
he deepest point in a trench is 24,997 feet below sea level. Elevations below sea level are represented by negative numbers. Part 1 out of 3 Enter the elevation of the trench. The elevation of the trench is feet.
pleasee help will give branielest
Answers
The trench descends to a depth of -24,997 feet below sea level, representing its remarkable depth below the surface.
The trench reaches a staggering depth of 24,997 feet below sea level, making it the deepest point in the area.
With elevations below sea level indicated by negative numbers, this particular trench plunges deep into the ocean floor.
Its immense depth is a testament to the remarkable geological features that exist beneath the surface of our planet.
The negative elevation signifies the significant extent to which this trench descends below the average sea level, providing an awe-inspiring example of the Earth's dynamic and diverse topography.
This extreme depth underscores the mysterious and captivating nature of our planet's oceans and their hidden wonders.
for such more question on surface
https://brainly.com/question/27987869
#SPJ11
Question 1. How many things can be represented with: (0.25 Mark) A. 6 bits B. 8 bits C. 11 bits D. 23 bits
Answers
With 6 bits, a total of 64 different combinations and with 8 bits, a total of 256 and with 11 bits, a total of 2048 different things and with 23 bits, a total of 8,388,608 different things can be represented.
The number of things that can be represented with a given number of bits can be determined by calculating the total number of possible combinations. Each bit has two possible states: 0 or 1. Therefore, for each additional bit, the total number of combinations doubles.
A. With 6 bits, there are \(2^{6}\) = 64 different possible combinations.
B. With 8 bits, there are \(2^{8}\) = 256 different possible combinations.
C. With 11 bits, there are \(2^{11}\) = 2048 different possible combinations.
D. With 23 bits, there are \(2^{23}\) = 8,388,608 different possible combinations.
In binary representation, each combination of 0s and 1s corresponds to a unique value. Therefore, the number of things that can be represented with a certain number of bits corresponds to the total number of unique values that can be represented.
Learn more about combinations here:
brainly.com/question/13715183
#SPJ11
What is the range of function g? g(x) = sqrt(x - 1) + 2
ОА. у >2
ОВ. у < 2
ОC. у <1
OD. у >1

Answers
Answer:
Answer OA. y >2
Step-by-step explanation:
I took the quiz on k12
Help ASAP Question:
The Department of Transportation's salt and sand mixing sheds are in the shape of a cone. One of the sheds measures 50 ft
high and 40 ft in diameter. What is the approximate volume of this shed? Use 3.14 for pi, Round to the nearest whole
number
Answers
Answer:
HI 56
Step-by-step explanation:
Realize the logical function OUT using CMOS logic (Switch-Switch)
_ _ _
OUT = c + (AB)
student submitted image, transcription available below
Build the truth table and the corresponding diagram.
Answers
CMOS logic gates can be implemented using transistors where the input signal is applied to the gate terminal of MOSFET (Metal Oxide Semiconductor Field Effect Transistor) and output is taken from the drain terminal of MOSFET.
Given: Logical function OUT = c + AB using CMOS logic (Switch-Switch)
We need to draw the truth table and the corresponding diagram for the given logical function using CMOS logic.
CMOS (Complementary Metal Oxide Semiconductor) technology is used to implement digital circuits with high speed and high noise immunity. It is widely used in VLSI technology.
The given logical function using CMOS logic is as follows.
OUT = c + (AB)
CMOS logic gates can be implemented using transistors where the input signal is applied to the gate terminal of MOSFET (Metal Oxide Semiconductor Field Effect Transistor) and output is taken from the drain terminal of MOSFET.
In CMOS technology, MOSFETs are used in pairs to implement logic gates as shown below:
Truth table for the given logical function using CMOS logic (Switch-Switch):
The truth table can be obtained by following the below steps:
Let c= 0 (open switch) then the expression becomes OUT = AB
Let A = 0 and B = 0, then OUT = 0+0=0
Let A = 0 and B = 1, then OUT = 0+0=0
Let A = 1 and B = 0, then OUT = 0+0=0
Let A = 1 and B = 1, then OUT = 0+1=1
Let c= 1 (closed switch) then the expression becomes OUT = 1+AB
Let A = 0 and B = 0, then OUT = 1+0=1
Let A = 0 and B = 1, then OUT = 1+0=1
Let A = 1 and B = 0, then OUT = 1+0=1
Let A = 1 and B = 1, then OUT = 1+1=1
The truth table is as follows:
Diagram for the given logical function using CMOS logic (Switch-Switch):
The corresponding circuit diagram for the given logical function using CMOS logic is as follows:
Therefore, the diagram for the given logical function using CMOS logic is as shown above.
To know more about CMOS logic gates, visit:
https://brainly.com/question/31657348
#SPJ11
I need help here is the problem

Answers
Answer:
12.96pi
Step-by-step explanation:
area = r^2 *pi
= 3.6^2 * pi
= 12.96pi
Step-by-step explanation:
area of a circle is = π r²
π × (3.6)²
= π × 12.96
= 12.96π
Simplify each expression using the properties of exponents and match it to the correct answer
Answers
help simplify:px-1 .px+1
Answers
Answer:
Answer is 1
Step-by-step explanation:
Helppp show work for brisnly

Answers
Answer:
18
Step-by-step explanation:
3/4 x 24 = 18
Use the figure to decide the type of angle pair that describes ∠5 and ∠2.
alternate exterior angles
same-side interior angles
corresponding angles
alternate interior angles

Answers
The type of angle pair that describes ∠5 and ∠2 is B Same-side interior angles.
How to illustrate the information given?It should be noted that same-side interior angles simply means when two lines that are parallel are interested by a transversal line.
It should be noted that the same-side interior angles are supplementary. This implies that they will be equal to 180°.
In this case, the type of angle pair that describes ∠5 and ∠2 is Same-side interior angles.
Learn more about angle on:
brainly.com/question/25716982
#SPJ1
Seven times the twice of a number and 6 equals 4
Answers
Answer:
7(2a+6) = 4
and the answer is:
19/7
Step-by-step explanation:
7(2a+6) = 4
7*2a + 7*6 = 4
14a + 42 = 4
14a = 4 - 42
14a = -38
a = -38/14
a = -19/7
Classify the following triangle. check all that apply. A: Acute B: Right C: Obtuse D: Equilateral E: Scalene F: Isosceles
Answers
Answer:
i think it's b
Step-by-step explanation:
Answer:
You didn't give us a picture of the triangle. In order to classify what type of triangle it is.
Step-by-step explanation:
how to calculate percent error when theoretical value is zero
Answers
Calculating percent error when the theoretical value is zero requires a slightly modified approach. The percent error formula can be adapted by using the absolute value of the difference between the measured value and zero as the numerator, divided by zero itself, and multiplied by 100.
The percent error formula is typically used to quantify the difference between a measured value and a theoretical or accepted value. However, when the theoretical value is zero, division by zero is undefined, and the formula cannot be applied directly.
To overcome this, a modified approach can be used. Instead of using the theoretical value as the denominator, zero is used. The numerator of the formula remains the absolute value of the difference between the measured value and zero.
The resulting expression is then multiplied by 100 to obtain the percent error.
The formula for calculating percent error when the theoretical value is zero is:
Percent Error = |Measured Value - 0| / 0 * 100
It's important to note that in cases where the theoretical value is zero, the percent error may not provide a meaningful measure of accuracy or deviation. This is because dividing by zero introduces uncertainty and makes it challenging to interpret the result in the traditional sense of percent error.
To learn more about percent error visit:
brainly.com/question/30545034
#SPJ11
I NEED HELP PLS THIS IS DUE TOMORROW

Answers
Answer:
6x -10 = 5x+12 (vertically opposite angles)
6x-5x =12+10
x= 22
Step-by-step explanation:
Pls mark as brainliest
Answer:
\(5x + 12 = 6x - 10 \\ 5x - 6x = - 10 - 12 \\ - x = - 22 \\ x = 22\)
Evaluate the expression when r = 10.
16 - r - 3
Answers
Answer:
The answer is 3
Step-by-step explanation:
Because 16 - 10 is 6. Then you minus 3 which is then 3 brainliset pls
Answer: 3
Step-by-step explanation:
r=10
16-(10)-3
=6-3
=3
based on this regression model, each additional family member increases the predicted costs by how much?
Answers
For the linera regression equation with dependent variable is monthly expenses for medical care while his independent variable is number of family members. See the above Excel output.
a) The prediction equation is y = 110.47 + 16.83x.
b) Based on his model, each additional family member increases the predicted costs by 16.83 times.
Linear regression equation is used to predict the dependent variable value based on the value of one or more independent variables. We have y, the dependent variable as monthly expenses for medical care and x, the independent variable as number of family members. From the Excel output are present in above figure and we need to find the predicted regression equation. The prediction linear regression equation is written as
a) From the above data the prediction equation is y = 110.47 + 16.83x --(1)
where, y --> monthly expenses
x --> number of family members
b) Based on this model, with an unit increase in family member, the predicted cost increases by 16.83 times. Hence, the required value is 16.83.
For more information about linear regression equation, visit :
https://brainly.com/question/30401933
#SPJ4
Complete question:
Bob White is conducting research on monthly expenses for medical care, including over-the-counter medicine. His dependent variable is monthly expenses for medical care while his independent variable is number of family members. above is his Excel output.
a) What is the prediction equation?
(b) Based on his model, each additional family member increases the predicted costs by how much?

Quadrilateral WXYZ is a rectangle. Diagonals WY and ZX intersect at P. If PY=3x−5 and WP=2x+11, find the value of ZP.
ZP=43
ZP=25
ZP=16
ZP=66
Answers
Answer:
The right answer is ZP = 43
Step-by-step explanation:
I just took the quick check
Please help will give brainiest
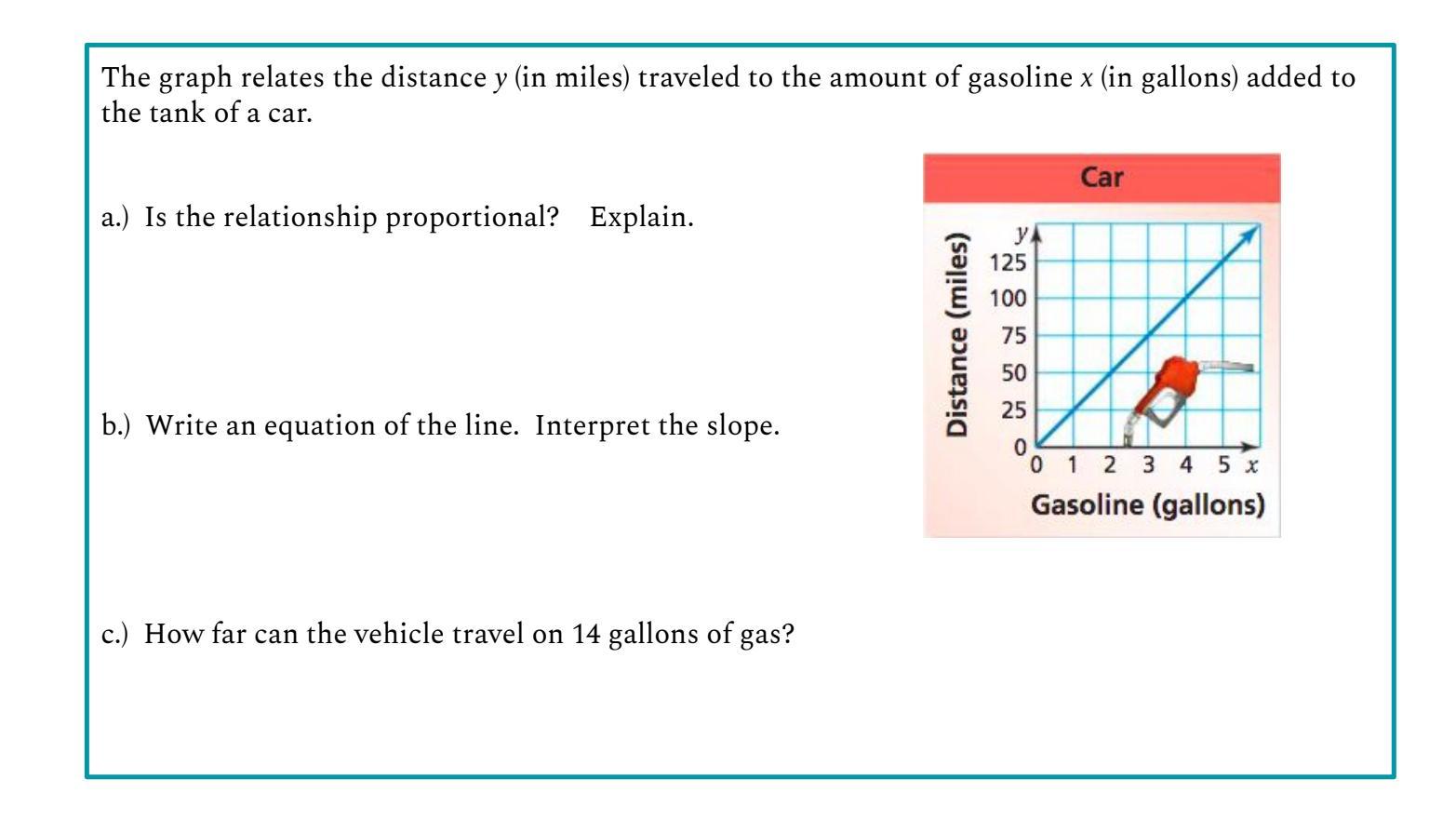
Answers
Answer:
a) Yes, the relationship is proportional.
b) \(y=25x\), slope is 25
c) 350 miles
Step-by-step explanation:
a) Proportional relationships are linear functions that pass through the origin.
b) Proportional relationships can be written as \(y=kx\), where \(k\) is a constant of proportionality. Substitute any point the line passes through to find this constant.
c) Substituting \(x=14\) into our function:
\(y=25x,\\y=25\cdot 14,\\y=\boxed{350}\)
What do you notice about the graph when it passess through a root of even multiplicity?
Answers
Please leave a thanks <3
If then find the second derivative, v" (t) = 2-1/4x^(3/2) v(t) = √√F-√t,
Answers
The second derivative is v''(t) = (3/4) (F-t)^(-7/4).
Given:
v(t) = √√(F-√t)
To find the second derivative v''(t), we first need to find the first derivative v'(t) of v(t):
v(t) = √√(F-√t)
v'(t) = d/dt [√√(F-√t)]
= d/dt [(F-t)^(1/4)]
= (1/4) (F-t)^(-3/4) (-1)
= (1/4) (F-t)^(-3/4)
Now, we can find the second derivative of v(t):
v'(t) = (1/4) (F-t)^(-3/4)
v''(t) = d/dt [(1/4) (F-t)^(-3/4)]
= (-3/4) (F-t)^(-7/4) (-1)
= (3/4) (F-t)^(-7/4)
Therefore, the second derivative is v''(t) = (3/4) (F-t)^(-7/4).
To know more about second derivative, click here
https://brainly.com/question/29005833
#SPJ11