Find the differential of the function. Z = e−4x cos(4πt)
Answers
The differential of the function Z is -4e⁻⁴ˣcos(4πt) - 4πsin(4πt)e⁻⁴ˣ
To find the differential function of Z = e⁻⁴ˣ cos(4πt), we will use the product rule of differentiation. The product rule states that the derivative of the product of two functions is equal to the first function multiplied by the derivative of the second function plus the second function multiplied by the derivative of the first function.
Let's apply the product rule to our function Z:
First, we differentiate the first function e⁻⁴ˣ with respect to x. The derivative of e⁻⁴ˣ is -4e⁻⁴ˣ.
Next, we differentiate the second function cos(4πt) with respect to t. The derivative of cos(4πt) is -4πsin(4πt).
Therefore, the differential function of Z is:
dZ/dt = -4e⁻⁴ˣcos(4πt) - 4πsin(4πt)e⁻⁴ˣ
To know more about differential function here
https://brainly.com/question/30074964
#SPJ4
Related Questions
The function h=−16t^2+1936 gives an object’s height h, in feet, at t seconds. When will the object be 912 feet above the ground?
Answers
next you can click 2nd trace then 5
which means the two will intersect at 8
(y=912 x=8)
meaning the object will be 912 feet above the ground at 8 seconds
What is the slope ? Simplify your answer and write it as a proper fraction

Answers
(0,80) (90,20)
Use Slope Formula m= (y1-y2)/(x1-x2)
90-80/20 = 1/2
Your slope is 1/2
Let P = 0.5 0.1 0.5 0.9 :] be the transition matrix for a Markov chain with two states. Let Xo = 0.5 0.5 be the initial state vector for the population. Find the steady state vector x. (Give the steady state vector as a probability vector.) X =
Answers
To find the steady state vector x, we must solve the equation xP = x, where P is the given transition matrix and x is the steady state vector.
P = | 0.5 0.1 |
| 0.5 0.9 |
Let x = (x1, x2). We have two equations:
1) 0.5x1 + 0.1x2 = x1
2) 0.5x1 + 0.9x2 = x2
Also, since x is a probability vector, we have:
3) x1 + x2 = 1
Now, we can solve the system of equations:
From equation (1): 0.5x1 = 0.1x2, so x1 = 0.2x2
Substitute x1 in equation (3): 0.2x2 + x2 = 1, which gives x2 = 1/1.2 = 5/6
Now, we can find x1: x1 = 0.2x2 = 0.2(5/6) = 1/6
Thus, the steady state vector x is (1/6, 5/6).
It is important to always be factually accurate, professional, and friendly, while being concise and avoiding extraneous amounts of detail. Typos and irrelevant parts of the question should be ignored. Here is the answer to the given student question:Let P = 0.5 0.1 0.5 0.9 :] be the transition matrix for a Markov chain with two states. Let Xo = 0.5 0.5 be the initial state vector for the population.
Find the steady state vector x. (Give the steady state vector as a probability vector.) X = [0.357 0.643]Explanation:Given transition matrix, P = 0.5 0.1 0.5 0.9Given initial state vector, Xo = 0.5 0.5The steady state vector x of the transition matrix P is given by X = [x1 x2] such that PX = X or (P-I)X=0 where I is the identity matrix of order 2.The matrix (P-I) is0.5-1 0.1 0.5 0.9-1which simplifies to-0.5 0.1 0.5 -0.1Applying R2→ R2+2R1 to the matrix (P-I), we get-0.5 0.1 0.0 -0.2Now, the equations are: -0.5x1 + 0.1x2 = 0.0, 0.5x1 - 0.2x2 = 0.0, and x1 + x2 = 1.Solving these equations, we get x1 = 0.357 and x2 = 0.643.Therefore, the steady state vector as a probability vector is X = [0.357 0.643].
Learn more about probability here: brainly.com/question/30034780
#SPJ11
If JL=17 and KL=14, what is LM?

Answers
Applying the leg rule, the length of LM is: 11.53 units
How to Apply the Leg Rule?The leg rule is applied when finding length of the legs or hypotenuse of a right triangle that has an altitude. It is given as:
Hypotenuse/leg = leg/part.
Given the following:
JL = 17 units (hypotenuse)KL = 14 units (leg)LM = ? (part)Plug in the values:
17/14= 14/LM
Cross multiply:
17(LM) = (14)(14)
17(LM) = 196
Divide both sides by 17
17(LM)/17 = 196/17
LM = 11.53 units
Learn more about the leg rule on:
https://brainly.com/question/26257841
#SPJ1
solve the 3 × 3 system shown below. enter the values of x, y, and z. x 2y – z = –3 (1) 2x – y z = 5 (2) x – y z = 4
Answers
The solution to the given system of equations is x = 2, y = -1, and z = 1.
What are the values of x, y, and z that solve the given system of equations?To solve the system of equations, we can use methods such as substitution or elimination. Here, we will use the method of elimination to find the values of x, y, and z.
First, let's eliminate the variable x by multiplying equation (1) by 2 and equation (3) by -1. This gives us:
2x + 4y - 2z = -6 (4)
-x + y - z = -4 (5)
Next, we can subtract equation (5) from equation (4) to eliminate the variable x:
5y - z = 2 (6)
Now, we have a system of two equations with two variables. Let's eliminate the variable z by multiplying equation (2) by 2 and equation (6) by 1. This gives us:
4x - 2y + 2z = 10 (7)
5y - z = 2 (8)
Adding equation (7) and equation (8), we can eliminate the variable z:
4x + 5y = 12 (9)
From equation (6), we can express z in terms of y:
z = 5y - 2 (10)
Now, we have a system of two equations with two variables again. Let's substitute equation (10) into equation (1):
x + 2y - (5y - 2) = -3
x - 3y + 2 = -3
x - 3y = -5 (11)
From equations (9) and (11), we can solve for x and y:
4x + 5y = 12 (9)
x - 3y = -5 (11)
By solving this system of equations, we find x = 2 and y = -1. Substituting these values into equation (10), we can solve for z:
z = 5(-1) - 2
z = -5 - 2
z = -7
Therefore, the solution to the given system of equations is x = 2, y = -1, and z = -7.
Learn more about: Equations,
brainly.com/question/29657983
#SPJ11
A student did an experiment to determine the number of letters recognized on an eye chart to see if it was affected by distance. What is the independent and dependent variable in this experiment?
Answers
Answer:
Independent variable: distance
Dependent variable: number of letters recognized on an eye chart
Step-by-step explanation:
Independent variables are stand-alone. This means that it does not depend on another variable but affects the dependent variable.
Dependent variables are dependent on another variable. When the independent variable changes, dependent variables are changed.
Since the hypothesis is that the distance affects the number of letters recognized,
the distance causes a change in the number of letters recognized not the other way around.
Thus, the dependent variable is the number of letters recognized on the eye chart while the independent variable is the distance.
Answer:
x and y
plz mark brainliest
Mark recorded the growth of a plant over 8 weeks. The equation y=0. 2x+2 represents the height y, in inches, after x weeks. How tall will the plant be after week 9?.
Answers
Answer:
3.8 inches
Step-by-step explanation:
y = 0.2x + 2 Substitute in 9 for x
y = 0.2(9) + 2
y = 1.8 + 2
y = 3.8
Nicloe bought a meal for $8 that has no sales tax she tips 20% what is the total amount including the tip
Answers
The normal curve with a mean of 0 and standard deviation of 1 is called ______________.
a. standard normal curve.
b. the emperical rule.
c. a random variable.
d. the z-value.
Answers
The normal curve with a mean of 0 and standard deviation of 1 is called (D) the z-value.
What is a standard score (z-value)?The z-score value indicates how many standard deviations you are from the mean. A z-score of 0 indicates that the data is on the mean. A positive z-score indicates that the raw score exceeds the mean average. For example, a z-score of +1 indicates that it is one standard deviation above the mean. The number of standard deviations by which the value of a raw score (that is, an observed value or data point) is above or below the mean value of what is being observed or measured is referred to as the standard score in statistics. Raw scores that are higher than the mean have positive standard scores, while those that are lower than the mean have negative standard scores.Therefore, the normal curve with a mean of 0 and standard deviation of 1 is called (D) the z-value.
Know more about standard scores here:
https://brainly.com/question/13579780
#SPJ4
It is known that 2x-3/x = x + 1 What is the value of x^2 -x + 3
Answers
The value of the equation x² - x + 3 is 37/9.
We have,
We can start by multiplying both sides of the equation by x:
2x - 3/x = x + 1
2x - 3 = x^2 + x
Rearranging and simplifying, we get:
x^2 - x + 3 = (2x - 3) + x^2
x^2 - x + 3 = x^2 + 2x - 3
-x + 3 = 2x - 3
5 = 3x
x = 5/3
Now we can substitute x into the equation x^2 - x + 3:
x^2 - x + 3 = (5/3)^2 - 5/3 + 3
x^2 - x + 3 = 25/9 - 15/9 + 27/9
x^2 - x + 3 = 37/9
Therefore,
The value of x² - x + 3 is 37/9.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
How much higher is -200 than 400 m?
Answers
Answer:
600m
Step-by-step explanation:
-200 + 200 = 0, 0 to 400 need 400, 400 + 200 = 600 i guess lol
Answer:
The answer is not greater because it is a negative. If you mean less than it is exactly 400 less than 400 m.
If 'a' and 'b' are two quantities (where a>b), represent their golden ratio algebraically. Illustrate the relationship between these quantities geometrically.
Answers
The golden ratio between quantities 'a' and 'b' can be represented algebraically as (a+b)/a = a/b = Φ. Geometrically, it is illustrated through the construction of a golden rectangle with sides in this ratio.
The golden ratio is a mathematical constant denoted by the Greek letter phi (Φ) and is approximately equal to 1.618. It is often represented algebraically as (a+b)/a = a/b = Φ.
To illustrate the relationship geometrically, we can use a geometric construction known as the golden rectangle. A golden rectangle is a rectangle that has the property that the ratio of its longer side to its shorter side is equal to the golden ratio.
Here's how we can construct a golden rectangle:
Start with a rectangle ABCD where AB is the longer side and BC is the shorter side.
Divide the longer side AB into two segments, AC and CB, such that the ratio of AB to AC is equal to the golden ratio (Φ). This means that AB/AC = Φ.
Draw a line segment DE parallel to AD and BC, where D is the intersection point of AC and DE.
Complete the rectangle DEFG by drawing lines through points E, F, and G parallel to AB and CD.
Now, we have a golden rectangle DEFG. The longer side EF is equal to AB, and the shorter side EG is equal to BC. The ratio of EF to EG is equal to the golden ratio (Φ). Geometrically, this illustrates the relationship between the two quantities (a and b) in the golden ratio.
It's worth noting that the golden ratio is found in various aspects of art, architecture, and nature. It is considered aesthetically pleasing and has been used in design principles to create visually harmonious compositions.
for such more question on golden ratio
https://brainly.com/question/2328454
#SPJ8
Subtract (4a2b - 3ab2 + 2ab + 5) and (2a2b + 3ab2 - 7ab). Choose the
difference.
2a4b2 - 5a2b2 + 5
2a 2b - 6ab2 + 9ab + 5
2a 2b - 6ab2 - 9ab + 5
2a2b - 5ab + 5
Answers
Answer:
2a2b-6ab2+9ab+5 is right answer
Find the area of the kite. Round to the nearest tenth.

Answers
The area of the kite is 90 sq.m.
Calculation
Area of the kite (quadrilateral) = \(\frac{product of their diagonal}{2}\) = \(\frac{pq}{2}\)
= \(\frac{12m*15m}{2}\) = \(\frac{180 sq.m}{2}\) = 90 sq.m.
What is the geometry of a kite?
The diagonals of every kite are orthodiagonal (at right angles), and when convex, they are tangential quadrilaterals (its sides are tangent to an inscribed circle). The quadrilaterals that are orthodiagonal and tangential are precisely convex kites. In addition to the squares, which are special examples of both right kites and rhombi, they also include the right kites, which have two opposite right angles, the rhombi, which have two diagonal axes of symmetry, and the squares.To learn more about kite geometry, refer to https://brainly.com/question/26870235
#SPJ1
Write out each step for converting 3 4/5 into an improper fraction (or a fraction greater than a whole).
1.
2.
3.
Answers
Answer:
19/5
Step-by-step explanation:
1. multiple 3 x 5= 15
2. add 15+4
3. put it over 5: 19/5
you would like to investigate whether smokers are more likely than non smokers to get lung cancer. you take the students in your class, select half at random and tell them to smoke a pack of cigarettes each day, and you tell the other half not to ever smoke. fifty years from now, you will analyze whether more smokers than non smokers get lung cancer. is this an experiment or an observational study? experiment observational study
Answers
An investigation whether smokers are more likely than non smokers to get lung cancer by grouping the class students into two groups is an example of experimental study.
Experimental Study: An experimental study is a study where the researcher has control over most of the variables. In contrast an observational study is a study where the researcher purely observes subject without controlling any variables. We have to investigate whether smokers are more likely than non-smokers to get lung cancer. Here the study is experimental study because the researcher/ we are trying to investigate the students of smokers and non-smokers. So, here control the members of the population that is students by randomly selecting them and dividing them in two groups (that is half -half) and provide one group cigarettes and not provide the other one. So, the above example of an experimental study. The following difficulties are come in study :
The results of the study are highly subjective due to possibilities of the human error.Experimental study is time consuming process with respect to its constraints.The participants i.e., experiment objects can be influenced by surroundings around them.Hence, the given problem is an example of experimental study.
For more information about experimental study, visit :
https://brainly.com/question/14393640
#SPJ4
After its first day of life, a baby blue whale started growing. It grew 47.075 inches. If the average baby grows at a rate of 1,5 inches a day, for how many days did the baby whale grow, to the nearest tenth of a day.
Answers
Answer:
31 days
Step-by-step explanation:
what i did is divided it
What type of correlation intensity exists between these two variables (weak, moderate, strong)?
Answers
Answer:
As a rule of thumb, a correlation greater than 0.75 is considered to be a “strong” correlation between two variables. However, this rule of thumb can vary from field to field. For example, a much lower correlation could be considered strong in a medical field compared to a technology field.
Step-by-step explanation:
in a certain population of fish, the lengths of the individual fish follow approximately a normal distribution with mean 54.0 mm and standard deviation 4.5 mm. we saw in example 4.3.1 that in this situation, 65.68% of the fish are between 51 and 60 mm long. suppose a random sample of four fish is chosen from the population. find the probability that
Answers
The probability that the average length of the four fish is between 51 and 60 mm is:
P(B) ≈ 0.658 .
Since the lengths of individual fish follow a normal distribution with mean 54.0 mm and standard deviation 4.5 mm, we can use the properties of the normal distribution to find the probabilities.
Let X be the length of a single fish. Then X follows a normal distribution with mean μ = 54.0 mm and standard deviation σ = 4.5 mm.
a) At least one fish in the sample is between 51 and 60 mm long:
Let A be the event that at least one fish in the sample is between 51 and 60 mm long. We want to find P(A).
The probability that a single fish is between 51 and 60 mm long is:
P(51 ≤ X ≤ 60) = P((51-54)/4.5 ≤ (X-54)/4.5 ≤ (60-54)/4.5) = P(-0.67 ≤ Z ≤ 1.11) ≈ 0.654
where Z is the standard normal variable.
Using the complement rule, the probability that none of the four fish are between 51 and 60 mm long is:
P(A') = P(no fish between 51 and 60 mm long) = (1 - 0.654)^4 ≈ 0.061
Therefore, the probability that at least one fish in the sample is between 51 and 60 mm long is:
P(A) = 1 - P(A') ≈ 0.939
b) The average length of the four fish is between 51 and 60 mm:
Let B be the event that the average length of the four fish is between 51 and 60 mm. We want to find P(B).
The distribution of the sample mean X is also normal with mean μ_X = μ = 54.0 mm and standard deviation σ_X = σ/√n = 4.5/√4 = 2.25 mm.
The probability that the average length of a sample of four fish is between 51 and 60 mm is:
P(51 ≤ X ≤ 60) = P((51-54)/(4.5/√4) ≤ (X -54)/(4.5/√4) ≤ (60-54)/(4.5/√4)) = P(-1.33 ≤ Z ≤ 0.89) ≈ 0.658
where Z is the standard normal variable.
Therefore, the probability that the average length of the four fish is between 51 and 60 mm is:
P(B) ≈ 0.658 .
Visit to know more about Probability:-
brainly.com/question/13604758
#SPJ11
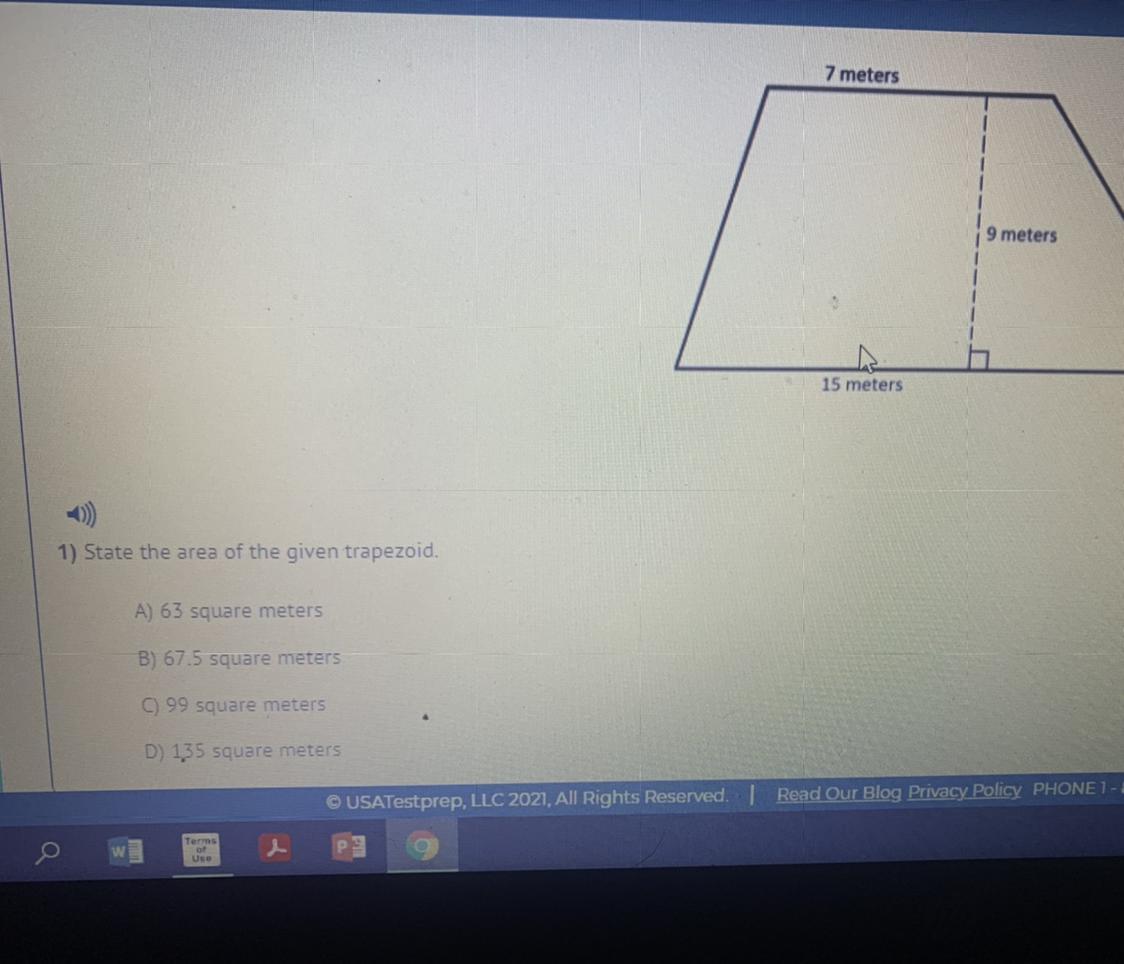
1) State the area of the given trapezoid.
7 meters
9 meters
15 meters
A) 63 square meters
B) 67.5 square meters
C) 99 square meters
D) 135 square meters
Answers
Answer:
a=99
Step-by-step explanation:
The answer is 99 square meters. I took this quiz, so I know the answers. I hope you get a good grade!!
Find the first four terms of the sequence represented by the expression -49 + 5n.
o-49, -54, -59,-64
-49, -44, -39, -34
o -49; -245; -1,225; -6,125
-44, -39, -34, -29
Answers
the first four terms of the sequence represented by the expression -49 + 5n are: -49, -44, -39, -34.
The expression -49 + 5n represents a sequence where each term is obtained by substituting different values for n and evaluating the expression.
Let's substitute the first four values of n (0, 1, 2, 3) into the expression to find the corresponding terms:
For n = 0:
-49 + 5(0) = -49 + 0 = -49
For n = 1:
-49 + 5(1) = -49 + 5 = -44
For n = 2:
-49 + 5(2) = -49 + 10 = -39
For n = 3:
-49 + 5(3) = -49 + 15 = -34
Therefore, the first four terms of the sequence represented by the expression -49 + 5n are:
-49, -44, -39, -34.
learn more about sequence here:
https://brainly.com/question/30262438
#SPJ11
What are the digits that repeat in the smallest sequence of repeating digits in the decimal equivalent of 2411?
Answers
Answer:
18
Step-by-step explanation:
A booster club paid for pizzas for an end of season party. They paid $13 for each pepperoni pizza and $11 for each plain pizza. The club bought a total of 18 pizzas for the party and paid a total of $212. Drag and drop the numbers to the boxes to create an equation which models this situation if x = the number of pepperoni pizzas and y = the number of plain pizzas bought.
Answers
Answer:
13x + 11y = 212
Step-by-step explanation:
total cost of purchasing an item = unit cost x total units purchased
total cost of purchasing pepperoni pizza = 13 × x = 13x
total cost of purchasing plain pizza = 11 × y = 11y
total cost of purchasing both items = total cost of purchasing pepperoni pizza + total cost of purchasing plain pizza
- 13x + 11y = 212
consider the following initial-value problem. y ′ 3y = e−3t, y(0) = 4 take the laplace transform of the differential equation and solve for ℒ{y}. (write your answer as a function of s.) ℒ{y} =
Answers
The Laplace transform to the initial-value problem is y(t) = (1/3) * e^(-3t).
To solve the given initial-value problem using Laplace transform, we'll apply the Laplace transform to both sides of the differential equation.
The Laplace transform of y' is denoted as ℒ{y'}.
Using the property of the Laplace transform, ℒ{y'} = sℒ{y} - y(0), where s is the Laplace variable and y(0) is the initial condition.
Applying the Laplace transform to the differential equation, we have:
ℒ{3y} = ℒ{e^(-3t)}
Using the linearity property of the Laplace transform and the table of Laplace transforms, we can find the transforms of each term:
3ℒ{y} = ℒ{e^(-3t)}
3ℒ{y} = 1/(s+3)
Now, we can solve for ℒ{y} by dividing both sides by 3:
ℒ{y} = 1/(3(s+3))
Therefore, the Laplace transform of y is ℒ{y} = 1/(3(s+3)).
To find the actual solution, we need to inverse Laplace transform the expression
ℒ{y} = 1/(3(s+3)).
Applying the inverse Laplace transform, we obtain the solution:
y(t) = (1/3) * e^(-3t)
Therefore, the actual answer to the initial-value problem is y(t) = (1/3) * e^(-3t).
Learn more about Initial-value Problem from the given link :
https://brainly.com/question/30402039
#SPJ11
4 , 15 , 30 , 49 , 72 , 99 , 130 what is the nth term would really appreciate help
Answers
Answer:
30 i think
Step-by-step explanation:
Factor this polynomial using the factor theorem.
x^2 + 6x+ 9

Answers
Answer:
(x+3)(x+3)
Step-by-step explanation:
I hopw this helps ;-)
what is the length of vw?

Answers
\( \frac{vz}{zy} = \frac{vw}{wx} \ \: \\ \\ \frac{16.5 }{27.5} = \frac{vw}{36} \)
so
vw= (16.5×36)÷27.5= 21.6
vw=21.6
I hope it helps
please mark brainliest ♡♡
At a certain point on a cliff-face, a rock-climber, Rob, observes the base of the cliff opposite to have an angle of depression of 60'. He also observes the top of the same cliff to have an angle of elevation of 40°. He knows that the distance from the base of the cliff he is climbing to the base of the opposite cliff is 110m. If the cliff that Rob is climbing is 30 m taller than other, find the height of the smaller cliff.
Answers
Answer:
283 m
Step-by-step explanation:
The tangent relation is useful for this.
Tan = Opposite/Adjacent
This tells us the distance from Rob's height to the ground on the other cliff is ...
tan(60°) = CB/CA
CB = CA·tan(60°) = 110·tan(60°)
Similarly, ...
tan(40°) = CD/CA
CD = CA·tan(40°) = 110·tan(40°)
Then the height of the smaller cliff is ...
BD = CB +CD = 110·(tan(60°) +tan(40°)) ≈ 282.8 m
The height of the smaller cliff is about 283 m.

If one item is chosen from m items, a second item is chosen from n items, and a third item is chosen from p items, the total number of three-item choices is?
Answers
If one item is chosen from m items, a second item is chosen from n items, and a third item is chosen from p items, the total number of three-item choices is MNP.
What is probability?
Probability can be regarded as a measure of the likelihood of an event that can take place.
It should be noted that Many events cannot be predicted with total certainty, hence , If one item is chosen from m items, a second item is chosen from n items, and a third item is chosen from p items, the total number of three-item choices is MNP.
Learn more about probability on:
https://brainly.com/question/24756209
#SPJ4
Find the slope and the y-intercept of the line.
- 9x+3y=-6
Answers
Answer:
slope is 3 and y intercept of -2
Step-by-step explanation: