Find the difference by subtracting the second polynomial from the first.(11m^(2)n^(5)-3m^(2)n^(3)+5mn-n ) and (-6m^(2)n^(5)+3m^(2)n^(5)+m+2n )
Answers
The difference between the two polynomials is 5m^(2)n^(5) - 3m^(2)n^(3) + 5mn + m + n.
To subtract the second polynomial from the first polynomial, we need to perform term-wise subtraction. Let's break down the process step by step:
The first polynomial is: 11m^(2)n^(5) - 3m^(2)n^(3) + 5mn - n.
The second polynomial is: -6m^(2)n^(5) + 3m^(2)n^(5) + m + 2n.
To subtract the second polynomial from the first, we need to change the signs of all terms in the second polynomial and then combine like terms.
First, let's change the signs of the terms in the second polynomial:
-(-6m^(2)n^(5) + 3m^(2)n^(5) + m + 2n) = 6m^(2)n^(5) - 3m^(2)n^(5) - m - 2n.
Now, we can combine like terms by adding or subtracting coefficients of similar monomials:
(11m^(2)n^(5) - 3m^(2)n^(3) + 5mn - n) - (6m^(2)n^(5) - 3m^(2)n^(5) - m - 2n)
= 11m^(2)n^(5) - 3m^(2)n^(3) + 5mn - n - 6m^(2)n^(5) + 3m^(2)n^(5) + m + 2n
= (11m^(2)n^(5) - 6m^(2)n^(5)) + (-3m^(2)n^(3) + 3m^(2)n^(5)) + (5mn + m) + (-n + 2n)
= 5m^(2)n^(5) - 3m^(2)n^(3) + 5mn + m + n.
Therefore, the difference between the two polynomials is 5m^(2)n^(5) - 3m^(2)n^(3) + 5mn + m + n.
In summary, to find the difference, we changed the signs of all terms in the second polynomial and then combined like terms with the first polynomial. The resulting polynomial is the difference between the two original polynomials.
For more such questions on polynomials , Visit:
https://brainly.com/question/4142886
#SPJ11
Related Questions
According to the historical data, the life expectancy in Argentina is equal to the life expectancy in Bolivia. A new study has been made to see whether this has changed. Records of 265 individuals from Argentina who died recently are selected at random. The 265 individuals lived an average of 74.8 years with a standard deviation of 4.1 years. Records of 300 individuals from Bolivia who died recently are selected at random and independently. The 300 individuals lived an average of 75.4 years with a standard deviation of 4.3 years. Assume that the population standard deviation of the life expectancy can be estimated by the sample standard deviations, since the samples that are used to compute them are quite large. At the 0.05 level of significance, is there enough evidence to support the claim that the life expectancy, μ1, in Argentina is not equal to the life expectancy, μ2, in Bolivia anymore? Perform a two-tailed test. Then fill in the table below.
Carry your intermediate computations to at least three decimal places and round your answers as specified in the table. (If necessary, consult a list of formulas.)
The null hypothesis: H sub 0:
The alternative hypothesis: H sub 1:
The type of test statistic:
The value of the test statistic:
The two critical values at the 0.05 level of significance:
Can we support the claim that the life expectancy in Argentina is not equal to the life expectancy in Bolivia? Yes or No
Answers
Answer:
Step-by-step explanation:
Hello!
The historical data suggests that the life expectancy in Argentina is equal to the life expectancy in Bolivia.
With the objective of testing if that it hasn't changed, the records of recently deceased people from Argentina and Bolivia were selected at random:
Group 1: Argentina
X₁: Years of life of a recently deceased Argentinian.
n₁= 265
X[bar]₁= 74.8 years
S₁= 4.1 years
Group 2: Bolivia
X₂: Years of life of a recently deceased Bolivian.
n₂= 300
X[bar]₂= 75.4 years
S₂= 4.3 years
The parameters of interest are the population means of the years of life of people in both countries:
H₀: μ₁ = μ₂
H₁: μ₁ ≠ μ₂
α: 0.05
The statistic to use is an approximate standard deviation, and since both samples are quite large, it is valid to use the sample standard deviations in place of the population standard deviations:
\(Z= \frac{(X[bar]_1-X[bar]_2)-(Mu_1-Mu_2)}{\sqrt{\frac{S^2_1}{n_1} +\frac{S_2^2}{n_2} } }\)≈N(0;1)
\(Z_{H_0}= \frac{(74.8-75.4)-(0)}{\sqrt{\frac{16.81}{265} +\frac{18.49}{300} } }= -2.54\)
The critical values for this test are:
\(Z_{\alpha /2}= Z_{0.025}= -1.96\)
\(Z_{1-\alpha /2}= Z_{0.0975}= 1.96\)
Using the critical value approach, the decision rule is:
If \(Z_{H_0}\) ≤ -1.96 or if \(Z_{H_0}\) ≥ 1.96, reject the null hypothesis.
If -1.96 < \(Z_{H_0}\) < 1.96, do not reject the null hypothesis.
\(Z_{H_0}\) ≤ -1.96 so the decision is to reject the null hypothesis.
So with a 5% significance level, there is enough evidence to reject the null hypothesis, you can conclude that the life expectancy in Argentina is different from the life expectancy in Bolivia.
I hope this helps!
this question is confusing to me please help..

Answers
Answer:
5
Step-by-step explanation:
First off find how many bowls and vases combined
12 bowls and 8 vases therefore 20
to find 1/4 of a number divide by 4
therefore, 20/4 is 5
Simplify (1/2)^4
1/10
1/8
1/4
Answers
Answer:
1/8
Step-by-step explanation:
\( \bigg( \frac{1}{2} \bigg)^{4} = \\ \\ = \frac{1}{8} \)
Ilya builds a slide that is 2.9 meters long. It is 1.5 meters above the ground. He wants to determine the distance from the bottom of the slide to the base of the ladder leading up to the slide. Which diagram represents this situation?
A triangle with side length 1.5 meters and hypotenuse 2.9 meters.
A triangle with side length 2.9 meters and hypotenuse 1.5 meters.
A triangle with side length 2.9 meters and hypotenuse 2.9 meters.
A triangle with side length 1.5 meters and hypotenuse 2.9 meters.
Answers
Answer:
the first one
Step-by-step explanation:
Answer:Option A is correct. (light blue color in the triangle choices)
In this triangle, the product of sin B and tan C is
90°
and the product of sin C and tan B is
Answers
In this triangle, the product of sin B and tan C is\(b^2/(ac)\) , and the product of sin C and tan B is \(c^2/(ab)\).
In a right-angled triangle ABC, where angle A is 90 degrees, we have the following side lengths:
AB = c (base)
BC = a (hypotenuse)
AC = b (perpendicular)
We need to calculate the products of sin B and tan C, and sin C and tan B.
First, let's calculate sin B and tan C:
sin(B) = opposite/hypotenuse = AC/BC = b/a
tan(C) = opposite/adjacent = AC/AB = b/c
The product of sin B and tan C is sin(B) * tan(C) = (b/a) * (b/c) = \(b^2\)/(ac).
Next, let's calculate sin C and tan B:
sin(C) = opposite/hypotenuse = AB/BC = c/a
tan(B) = opposite/adjacent = AB/AC = c/b
The product of sin C and tan B is sin(C) * tan(B) = (c/a) * (c/b) = \(c^2\)/(ab).
Therefore, in the given right-angled triangle ABC, the product of sin B and tan C is\(b^2\)/(ac), and the product of sin C and tan B is \(c^2\)/(ab).
These formulas hold true for any right-angled triangle, where the base is AB, the hypotenuse is BC, and the perpendicular is AC.
For more such information on: triangle
https://brainly.com/question/29869536
#SPJ8
The question probable may be:
In this triangle, the product of sin B and tan C is _____ , and the product of sin C and tan B is _______.

Find the 70th term of the following arithmetic sequence.
17, 20, 23, 26,
Answers
Answer:
Since it starts at 17 and is increasing by 3 each time, the 70th term will be:
17 + 3(70) =
17 + 210 =
227
In conclusion, 227 would be the 70th term in the sequence.
Step-by-step explanation:
Have a great rest of your day
#TheWizzer

Step-by-step explanation:
Tn = a + (n - 1)d
n = 70, a = 17, d = > 20 - 17 => 3
T_70 = 17 + (70 - 1)3
T_70 = 17 + 69•3
T_70 = 17 + 207
T_70 = 224
The capacity of a water tank is 10000 litres and there is 4800 litres of water. A water tap can fill 40 litres of water per minute and another tap can empty 25 litres of water per minute. If both the taps are opened together for 10 minutes, then how much water will be in the tank after 10 minutes?
Answers
The amount of water tank with water after 10 minutes will be 4950 liters.
To solve this problem, we need to keep track of the net flow of water into the tank over the course of 10 minutes. The tap filling water adds water to the tank, while the tap emptying water removes water from the tank.
Let's calculate the net flow rate of water per minute:
Flow rate = (filling tap flow rate) - (emptying tap flow rate)
Flow rate = 40 L/min - 25 L/min
Flow rate = 15 L/min
Now, we can calculate the net flow of water over 10 minutes:
Net flow of water = (flow rate) * (time)
Net flow of water = 15 L/min * 10 min
Net flow of water = 150 L
Therefore, over the course of 10 minutes, the net flow of water into the tank is 150 liters.
Initially, the tank had 4800 liters of water. Adding the net flow of water, we can determine the final amount of water in the tank:
Final amount of water = (initial amount of water) + (net flow of water)
Final amount of water = 4800 L + 150 L
Final amount of water = 4950 L
After 10 minutes, there will be 4950 liters of water in the tank.
for similar questions on water tank.
https://brainly.com/question/30723760
#SPJ8
The diameter of the circle below measures 7 cm,
What is the approximate area of the circle?
A. 14 cm2
B. 22 cm2
C. 38 cm2
D. 154 cm2
Answers
Answer: D
Step-by-step explanation:
Remember the formula -
\(A = \pi\) × \(r^{2}\)
π = 3.14
\(r^{2}\) = 7
7² = 49
3.14 x 49 = 153.94
A = π · r² = π · 72 ≈ 153.93804
153.93804 ⇒ 154 (rounded)
Your answer is D.
you are 6 1/2 feet below sea level. you swim towards the surface 2 2/3 feet. what is your new position the water?
Answers
Please help I need this will give 100 points please help

Answers
The solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Solving Inequality in a given domainGiven the inequality,
f(x²-2) < f(7x-8) over D₁ = (-∞, 2)
We need to find the values of x that satisfy this inequality.
Since we know that f is increasing over its domain, we can compare the values inside the function to determine the values of x that satisfy the inequality.
First, we can find the values of x that make the expressions inside the function equal:
x² - 2 = 7x - 8
Simplifying, we get:
x² - 7x + 6 = 0
Factoring, we get:
(x - 6)(x - 1) = 0
So the values of x that make the expressions inside the function equal are x = 6 and x = 1.
We can use these values to divide the domain (-∞, 2) into three intervals:
-∞ < x < 1, 1 < x < 6, and 6 < x < 2.
We can choose a test point in each interval and evaluate
f(x² - 2) and f(7x - 8) at that point. If f(x² - 2) < f(7x - 8) for that test point, then the inequality holds for that interval. Otherwise, it does not.
Let's choose -1, 3, and 7 as our test points.
When x = -1, we have:
f((-1)² - 2) = f(-1) < f(7(-1) - 8) = f(-15)
Since f is increasing, we know that f(-1) < f(-15), so the inequality holds for -∞ < x < 1.
When x = 3, we have:
f((3)² - 2) = f(7) < f(7(3) - 8) = f(13)
Since f is increasing, we know that f(7) < f(13), so the inequality holds for 1 < x < 6.
When x = 7, we have:
f((7)² - 2) = f(47) < f(7(7) - 8) = f(41)
Since f is increasing, we know that f(47) < f(41), so the inequality holds for 6 < x < 2.
Therefore, the solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Learn more about inequality here:
https://brainly.com/question/25944814
#SPJ1
What are the points of the image of the line in Q4 after the dilation?

Answers
Note that the coordinates of the point A' after rotating 90 degrees clockwise about the point (0,1) are (3, -4). (Option B)
How is this so ?To rotate a point 90 degrees clockwise about a given point,we can follow these steps -
Translate the coordinates of the given point so that the center of rotation is at the origin. In this case,we subtract the coordinates of the center (0,1) from the coordinates of point A (5,4) to get (-5, 3).
Perform the rotation by swapping the x and y coordinates and changing the sign of the new x coordinate. In this case,we swap the x and y coordinates of (-5, 3) to get (3, -5).
Translate the coordinates back to their original position by adding the coordinates of the center (0,1) to the result from step 2. In this case, we add (0,1) to (3, -5) to get (3, -4).
Therefore, the coordinates of the point A' after rotating 90 degrees clockwise about the point (0,1) are (3, -4).
Learn more about coordinates at:
https://brainly.com/question/17206319
#SPJ1
Find the slope of the line passing through the points (-4,6) and (3,6)
Slope:
Find the slope of the line passing through the points (-5,8) and (-5,-6)
Slope:
Answers
1. 0
2. Undefined
Explanation:
To find the slope of the two points, you first have to subtract the y1 from the y2 (6-6). Then, you do the same thing with the x1, and the x2 (3-(-4). Your slope is 0/7. 0/7 simplified is 0, since the 0 is the numerator, not the denominator.
Next, you can do the same thing with the second slopes. First is -6-8, which is the numerator, and then do -5-(-5), which is the denominator. Your answer comes out to -14/0. If the denominator is 0, the answer is will always be undefined.
Hope that helped!!
Required answer:
0Not DefinedDetailed explanation:
To find the slope of the line, given that it passes through two points, use the formula:
\(\bf{m=\dfrac{y_2-y_1}{x_2-x_1}}\)
Where:
m = slopePlug in the data:
\(\bf{m=\dfrac{6-6}{3-(-4)}=\dfrac{0}{3+4}=\dfrac{0}{7}=\boxed{\bf{0}}\)
- - - - - - - - - - - - - - - - - - - - - -
Given the pair of points: (-5,8) and (-5,-6), plug them into the slope formula:
\(\bf{m=\dfrac{y_2-y_1}{x_2-x_1}}\)
Evaluate:
\(\bf{m=\dfrac{-6-8}{-5(-5)}=\dfrac{-14}{-5+5}=\dfrac{-14}{0}=\boxed{\bf{Not\:De fined}}\)
- - - - - - - - - - - - - - - - - - - - - - -
An odometer shows that a car has traveled 41,00$ miles by January 1, 2020. The car travels 19,000 miles each year. Write an equation that represents the number y of miles on the car’s odometer x years after 2020.
Answers
The required equation for number of miles and years for the car is given as; y = 19000x + 41000
How to represent a linear equation?To represent a straight line on a graph consider two points namely x and y intercepts of the line. To find x-intercept put y = 0 and for y-intercept put x = 0. Then draw a line passing through these two points.
The parameters are;
Suppose the year 2020 represents x = 0.
The distance travelled per year can be taken as the slope of the linear equation. Thus, slope = 19000.
And, the distance travelled by January 1, 2020 is 41000.
This tells us that for x = 0, y = 41000.
The linear equation in slope intercept form is given as;
y = mx + c
where;
m is slope
c is y-intercept
Substitute the corresponding values in the above equation to obtain,
y = 19000x + c
At x = 0, y = 41000
41000 = (19000 × 0) + c
c = 41000
Now, the equation can be written as,
y = 19000x + 41000
Read more about Linear Equation at; https://brainly.com/question/28732353
#SPJ1
The following bar chart shows the distances run by Jay's family in a race.
Find the median distance in km.

Answers
The median of the distances is M = 6.5 kilometers
Given data ,
To find the median of a set of numbers, we arrange the numbers in ascending order and then locate the middle value. If there is an odd number of values, the median is the middle number. If there is an even number of values, the median is the average of the two middle numbers.
Arranging the given set of numbers in ascending order: {4, 5, 8, 11}
Since the set has an even number of values, the median is the average of the two middle numbers. In this case, the two middle numbers are 5 and 8. To find the average, we add these two numbers and divide by 2:
(5 + 8) / 2 = 13 / 2 = 6.5
Hence , the median of the given set {4, 5, 8, 11} is 6.5
To learn more about median click :
https://brainly.com/question/28687994
#SPJ1
Please show work and thank you

Answers
The value of the perpendicular side d = 8.66 inches.
What is the Pythagorean theorem?Pythagorean theorem states that in the right angle triangle the hypotenuse square is equal to the square of the sum of the other two sides.
Given that:-
Base = 5 in
Angle = 60
By using trigonometry property:-
\(tan\theta =\dfrac{d}{B}\\\\\)
d = B x tan60
d = 5 x tan60
d = 8.66 in
Hence the value of the perpendicular side d = 8.66 inches.
To know more about the Pythagorean theorem follow
https://brainly.com/question/343682
#SPJ1
Please help me!!!! How do I graph the equation ? I got the first three parts right. I will award brianieust and crown

Answers
i can help, but i need to know the equation.
is it in slope intercept form or something?
HURRY PLEASE?!
Determined to finish her milkshake before Diego, Lin now drinks her 12 ounce milkshake at a rate of 13 an ounce per second. Diego starts with his usual 20 ounce milkshake and drinks at the same rate as before, 23 an ounce per second.
Below is a graph of this system.
After how many seconds do both Diego and Lin have the same amount of milkshake left?
[ Select ]
How many ounces do both Diego and Lin have left of their milkshakes at that point?
[ Select ]

Answers
Answer: 24 seconds
4 ounces
Answer:
24 seconds and 4 ounces
Step-by-step explanation:
The point where both lines meet is the point where they are both equal.
The point where both lines meet is (24,4)
Since the x-axis represents seconds the x-coordinate will represent the number of seconds it takes for them to be equal which is 24.
Since the y-axis represents ounces the y-coordinate will represent the number of ounces they have when they are equal which is 4.
Westside Energy charges its electric customers a base rate of $8.00 per month, plus 12¢ per kilowatt-hour (kWh) for the first 300 kWh used and 4¢ per kWh for all usage over 300 kWh. Suppose a customer uses x kWh of electricity in one month. Express the monthly cost E as a piecewise defined function of x. (Assume E is measured in dollars.)

Answers
The linear function that gives the monthly cost E for x > 300 is given by:
E(x) = 44 + 0.04x.
What is a linear function?A linear function is modeled by:
y = mx + b
In which:
m is the slope, which is the rate of change, that is, by how much y changes when x changes by 1.b is the y-intercept, which is the value of y when x = 0, and can also be interpreted as the initial value of the function.When x > 300, we have that:
The base rate of $8.00 was paid.The 12 cents for each kWh up to 300 was paid.Hence the intercept is given by:
b = 8 + 0.12 x 300 = 44.
The slope is the cost per kWh of 4 cents, hence the function is:
E(x) = 44 + 0.04x.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Solve the following quadratic inequality x^2+x-6>0
Answers
Answer:
x < -3 or x > 2
Step-by-step explanation:
x² + x - 6 > 0
Convert the inequality to an equation.
x² + x - 6 = 0
Factor using the AC method and get:
(x - 2) (x + 3) = 0
If any individual factor on the left side of the equation is equal to 0, the entire expression will be equal to 0.
x - 2 = 0
x = 2
x + 3 = 0
x = -3
So, the solution is x < -3 or x > 2
Two more than four times a number is -10.
Answers
Answer:
Two more than four times -2 is -10.
Step-by-step explanation:
Solve the equations for x

Answers
Answer:
Step-by-step explanation:
5=cx-ax=x(c-a)
x(c-a)/5=1
(c-a)/5=1/x
x=5/(c-a)
Quickly Please!
Which equation has the solutions x = StartFraction 5 plus-or-minus 2 StartRoot 7 EndRoot Over 3 EndFraction?
3x2 – 5x + 7 = 0
3x2 – 5x – 1 = 0
3x2 – 10x + 6 = 0
3x2 – 10x – 1 = 0
Answers
Answer:
3x^2-10x+6=0
Step-by-step explanation:
3x^2-10x+6=0
Δ=10^2-4*3*6=100-72=28
V28=V4*7=2V7
x1=(10+2V7)/6=2(5+V7)/6=(5+V7)/3
x2=(5-V7)/3
Answer:
d
Step-by-step explanation:
edge
Chris's gross monthly earning is $3000. Calculate his net pay (take-home pay) by using the deductions below.
Federal Tax: 12%
State Tax: 3%
Local Tax: 1%
Social Security Tax: 6%
Medicare Tax: 6%
$3000
$2160
$840
$2200
Answers
3000=100%
x=12%
3000•12=100•x
x=360
2) calculate 3% of 3000
3000=100%
y=3%
3•3000=100y
y=90
3) calculate 1% of 3000
3000=100%
z=1%
3000•1=100z
z=30
4) calculate 6% of 3000
3000=100%
k=6%
3000•6=100k
k=180
5) now we need to add all this numbers to each other to see total money he has to spend in taxes (but we will take 180 twice because there where two 6%_s)
360+90+30+180+180=840
6) to calculate his take-home pay, we need to subtract 3000 by tax pay that we just calculated
3000-840=2160
FINALL ANAWER—his take home pay is $2160
Answer:
$2160
Step-by-step explanation:
federal tax = 12%of $3000
=12/100×3000
=12×30
=$360
state tax=3%of$3000
=3/100×3000
=3×30
=$90
local tax=1%of$3000
=1/100×3000
=1×30
=$30
social security tax=6%of$3000
=6/100×3000
=6×30=180
similarly, Medicare tax=180
add them all and subtract with monthly earning
$360+$90+$30+$180+$180=$840
$3000-$840=$2160
so total deduction is $2160
Kayla read 12 1/2 pages on Friday. she did 3/4 of her reading before dinner. how many pages did she read before dinner (equation)
Answers
Answer:
Number of pages Kayla read before dinner = \(9\frac{3}{8}\) pages
Step-by-step explanation:
Given:
Total number of pages Kayla read on Friday = \(12\frac{1}{2}\) = 25/2 pages
Number of pages Kayla read before dinner = [3/4][Total pages she read]
Find:
Number of pages Kayla read before dinner
Computation:
Number of pages Kayla read before dinner = [3/4][Total pages she read]
Number of pages Kayla read before dinner = [3/4][Number of pages Kayla read before dinner]
Number of pages Kayla read before dinner = [3/4][25/2]
Number of pages Kayla read before dinner = 75/8
Number of pages Kayla read before dinner = \(9\frac{3}{8}\) pages
Find the value of y. Round your answer to the nearest tenth
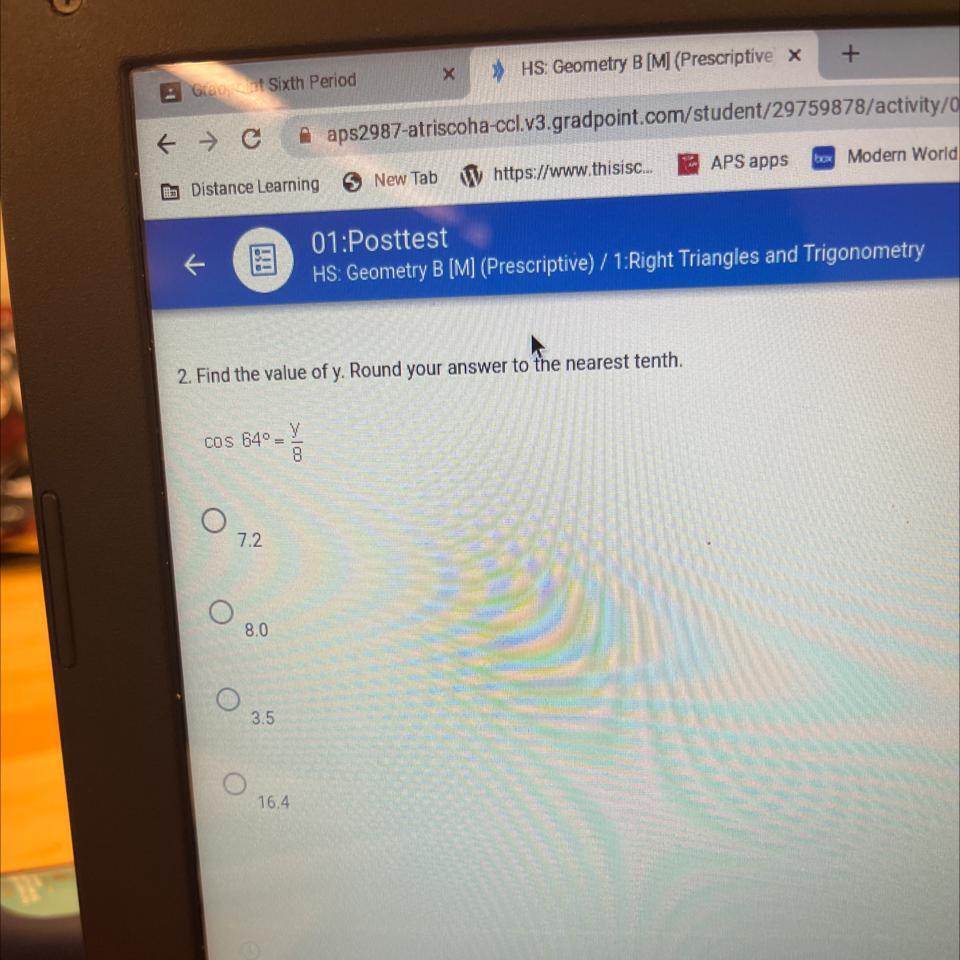
Answers
The value of y from the given expression is 3.5
Trigonometry equationsGiven the trigonometry equation below;
cos 64 = y/8
Cross multiply to have:
y = 8cos64
Simplify
y =8(0.438)
y = 3.506
Hence the value of y from the given expression is 3.5
Learn more on expression here: https://brainly.com/question/723406
#SPJ1
I need help with this ! Anything helps.

Answers
X=85
No.6
X=80
No.7
X=10
No.8
X=6
No.9
X= -9
No.10
X=29
No.11
X= -6
No.12
X= -7
Hope this helps
Help with this soon as possible.

Answers
The set of numbers that represent the domain of the function in the table of values given is: A. {-1, -2, -3}.
What is the Domain of a Function?A function has domain elements and corresponding range elements. All the x-values make up the set of elements that fall under the domain of the function while all the y-values make up the range of the function.
In the table of values given, all the set of numbers under x represent the domain of the function while all the set of numbers under y represent the range of the function.
Therefore, the set of numbers that represent the domain of the function in the table of values given is: A. {-1, -2, -3}.
Learn more about the domain of function on:
https://brainly.com/question/1369616
#SPJ1
Data from 2011 indicates that NYC has a total population of 8,244,910 people. The population of Queens is about 23.3% of the total population of NYC (population data is from 2011). Calculate this value for all 5 boroughs.
• Bronx has a population of 1,392,002. What is its percent of the total NYC population?
%
• Broklyn has a population of 2,532,645. What is its percent of the total NYC population?
%
• Manhattan has a population of 1,601,948.
What is its percent of the total NYC
population?
%
• Queens has a population of 2,247,848. What is its percent of the total NYC population?
27.26
%
• Staten Island has a population of 470,467.
What is its percent of the total NYC
population?
Answers
The appropriate percentage of the cities in NYC will be:
Bronx = 16.88%
Brooklyn = 30.72%
Manhattan = 19.43%
Queens = 27.26%
Staten Island = 5.71%
How to illustrate the information?NYC has a total population of 8,244,910 people.
Bronx has a population of 1,392,002, the percent of the total NYC population will be:
= 1,392,002 / 8,244,910 × 100
= 16.88%
Broklyn has a population of 2,532,645, its percent of the total NYC population will be:
= 2532645 / 8244910 × 100
= 30.72%
Manhattan has a population of 1,601,948, its percent of the total NYC population will be:
= 1601948 / 8244910 × 100
= 19.43%
Queens has a population of 2,247,848, its percent of the total NYC population will be:
= 2,247,848 / 8244910 × 100
= 27.26%
Staten Island has a population of 470,467, its percent of the total NYC population will be:
= 470467 / 8244910 × 100
= 5.71%
Learn more about percentages on:
brainly.com/question/24877689
#SPJ1
Solve (x+1)2 =13/4 using the square root property
Answers
Answer:
Starting with the equation:
(x + 1)^2 = 13/4
We can use the square root property, which states that if a^2 = b, then a is equal to the positive or negative square root of b.
Taking the square root of both sides, we get:
x + 1 = ±√(13/4)
Simplifying under the radical:
x + 1 = ±(√13)/2
Now we can solve for x by subtracting 1 from both sides:
x = -1 ± (√13)/2
Therefore, the solutions to the equation are:
x = -1 + (√13)/2 or x = -1 - (√13)/2
Step-by-step explanation:
Answer these two questions ASAP please, help is appreciated.


Answers
Answer:
B and A
Step-by-step explanation:
(A question needs two answers so the asker can have the brainliest option)
Best of luck