Find the cube of each semimajor axis length (A) by raising the value to the third power. Write your results in the table provided. Round all values to the nearest thousandth. Consult the math review if you need help with exponents

Nonnegativity conditions impose b. upper bounds on the decision variables in an optimization problem.  The correct answer is b. Upper bounds on the decision variables.

They ensure that the variables cannot take negative values and are typically used when the variables represent quantities that cannot be negative, such as quantities of goods or resources.

By setting an upper bound of zero or a positive value, the nonnegativity condition restricts the feasible region of the optimization problem to only include nonnegative values for the decision variables.

This is a common constraint in many optimization models to reflect real-world limitations or practical considerations.

for such more question on variables

https://brainly.com/question/19803308

#SPJ8

Answer:

w 2 x 6

Step-by-step explanation:

Considering the given probability distributions, distribution D is valid.

A probability distribution is valid if:

In this problem, only distribution D has a sum of 1, hence it is the only valid distribution.

More can be learned about probability distributions at brainly.com/question/23670007

#SPJ1

Answer:

Probability distribution D is shown. The probability of 1 is 0.2; 2 is 0.1; 3 is 0.1; 4 is 0.5; 5 is 0.1.

Step-by-step explanation:

The answer above is correct.

Answer:

a

Step-by-step explanation:

Answer:

no value of X so no answer

Step-by-step explanation:

Answer: try the US cellar field

Home plate is 400ft

Field fence height is 8ft

Angel of elevation is 0.85

Answer:

Part A-

Answer- f(x) is the profit made from selling 'x' number of salads.

Part B-

Question- Identify and interpret the key features of the function in the context of the situation you described in part A.

Answer-

End behavior- As 'x' approaches 25, f(x) approaches 20. As 'x' approaches 1, f(x) approaches 4.

Domain- 1, 4, 9, 16, 25

Range- 4, 8, 12, 16, 20

x and y- intercepts- None

Maximum- 20

Minimum- 4

Step-by-step explanation:

Mark as brainliest please :)

Answer:

D

Step-by-step explanation:

f(x)=x-14     g(x)=x^2+14

fog=f(g(x)

=f(x^2-+14)

=f(x^2+14)-14

fog(x)=x^2

The percentage of the variability does the model accounts for with the data is equals to the 40%.

We have an article in wear (1992, vol. 152, pp. 171-181), x = oil viscosity, y = wear volume and we have a table consists data values of x and y.

the simple linear regression model, is represented as

\(y = \beta_0 + \beta_1x \)

where,

\(\beta_0 \)

= intercept

\(\beta_1\)

= slope

The above shows all calculations of these variables.

Hence, required value is 40%.

For more information about percentage of the variability, visit :

#SPJ4

Answer:

14/3

Step-by-step explanation:

Flip the second fraction's numerator and denominator to get its reciprocal of 7/3. Then, you simply multiply it by 2, which equals 14/3.

Answer:

2/10 or 0.2

i dont know which tenths you wanted so i did both

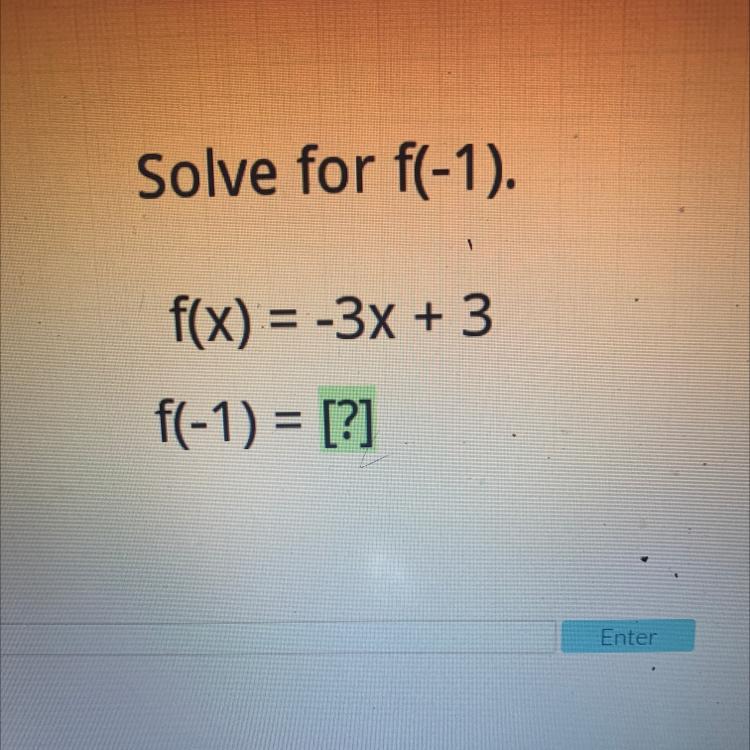
Answer:

Step-by-step explanation:

We know that the area of a triangle is given by :-

Let b be the base (in feet)  of the triangle .

it is given that  , The school wants the height of the triangle to be 6 feet.

Then, the area of triangle will be :-

           (1)

The area of the logo must be at most (less than or equal to) 15 square feet.

i.e. Area ≤ 15 square feet         (2)

Now, Substitute the value of A from (1) into (2) , we get

Divide both sides by 3  , we get

ANSWER

N = 11

EXPLANATION

Given:

3N + 5 = 38

Desired Outcome:

Value of N

Solve for N

Hence, the value of N is 11.

We are given the following equation and we must state the reason behind each of the steps taken to solve it:

In the first step after giving the equation 21 is being substracted from both sides of the equation. Remember that the substraction property of the equality states that any value substracted from one side of the equal sign must also be substracted from the other side. Therefore the reason behind this step is the substraction property.

Then the substractions on each side are performed. In the left side we get 21-21=0 so the constant term dissapears and on the right we obtain 21-15=6. This means that during this step only a simplification was performed.

In the following step a number 2 is multiplied to each side of the equal sign. Remember that the multiplication property of equality states that whatever is multiplied in one side of the equal sign must also be multiplied in the other side. Then the reason behind this step is the multiplication property of equality.

In the final step in the left side the 2 multiplying is simplified with the number 2 dividing and in the right side the product between -6 and 2 is performed. Then this step is also a simplification.

Then the reasons in order are:

- Substraction Property of Equality

- Simplifying

- Multiplication Property of Equality

- Simplifying

The efficiency of the Zumba class system is approximately 69.2%, and its utilization is approximately 54.5%.

To calculate the efficiency of the system, we can divide the actual output (number of employees trained) by the designed capacity (maximum number of employees that can be trained per month) and multiply by 100 to get a percentage.

Efficiency = (Actual Output / Designed Capacity) * 100

Efficiency = (600 / 850) * 100 = 70.6%

Therefore, the efficiency of the system is approximately 70.6%.

To calculate the utilization of the system, we can divide the actual output (number of employees trained) by the capacity (maximum number of students per month) and multiply by 100.

Utilization = (Actual Output / Capacity) * 100

Utilization = (600 / 1100) * 100 = 54.5%

Therefore, the utilization of the system is approximately 54.5%.

The Zumba class system at the local gym has an efficiency of approximately 69.2% and a utilization rate of approximately 54.5%. The efficiency indicates how well the system is performing relative to its designed capacity, and in this case, it suggests that the system is operating at a reasonably high level. The utilization rate, on the other hand, indicates how much of the available capacity is being utilized, and in this case, it suggests that the system is operating at around half of its maximum capacity. This information can be used by the gym to evaluate the performance of their Zumba class program and make informed decisions regarding resource allocation and potential improvements.

To know more about Efficiency, visit

https://brainly.com/question/15418098

#SPJ11

Answer:

stinkey monkey :3

The equivalent fraction to -5/25 will be -1/5. Since the value of both fractions is the same as a result represented as the equivalent fraction.

Fraction number consists of two parts, one is the top of the fraction number which is called the numerator and the second is the bottom of the fraction number which is called the denominator.

It is given that the expression is, -5/25.

We have to find the equivalent fraction for the given expression.

Equivalent fractions are two or more fractions that, although having various numerators and denominators, are all the same. 1/5, for instance, is equal to  -5/25. The fraction is always expressed in its simplest form, "one-fifth."

Thus, the equivalent fraction to -5/25 will be -1/5. Since the value of both fractions is the same as a result represented as the equivalent fraction.

Learn more about the fraction here:

brainly.com/question/1301963

#SPJ6

The probabilities are given as follows:

a) Square: 1/6.

b) Not the triangle: 43/48.

A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.

The total area of the figure is given as follows:

12 x 8 = 96 units². (rectangle).

The area of the square is given as follows:

4² = 16 units² (square of the side lengths).

Hence the probability of the square is given as follows:

p = 16/96

p = 1/6.

The area of the triangle is given as follows:

A = 0.5 x 4 x 5 = 10 units². (half the multiplication of the side lengths).

Hence the complement of the area of the triangle is of:

96 - 10 = 86 units².

And the probability of the complement is of:

86/96 = 43/48.

More can be learned about probability at https://brainly.com/question/24756209

#SPJ1

Answer:

6. k = 7/6

12. c = 2.06 if it wrong tell me because I'm not really sure

Answer:

12.56 mm²

Step-by-step explanation:

\(A=\pi r^{2}\)

Plug the given values into the area equation

\(A=3.14*2^{2}\\A=3.14*4\\A=12.56\)

Therefore, the area of the circle is 12.56 mm².

I hope this helps!

Step-by-step explanation:

We can use long division to divide the polynomial (4x³ - 6x² - 4x + 8) by the binomial (2x - 1).

2x² + 2x - 4

2x - 1 | 4x³ - 6x² - 4x + 8

- (4x³ - 2x²)

---------------

-4x² - 4x

+ ( -4x² + 2x )

--------------

-2x + 8

- (-2x + 1)

----------

7

Therefore, the quotient is 2x² + 2x - 4, and the remainder is 7.

We will solve as follows:

*First: We find out the value of the product:

Now, we find out from the other expressions:

*First:

[No]

*Second:

[Yes]

*Third:

[Yes]

*Fourth:

[No]

*Fifth:

[Yes]

The statement that f has a simple zero at z=0 and vanishes nowhere else in |z|≤1 implies that the function f is non-vanishing and has a derivative that does not vanish at z=0.

From this, we can use the Implicit Function Theorem which states that if f is holomorphic in a neighborhood of a point (a,b) and f(a,b)=0 and ∂f/∂y(a,b)≠0, then there exists an open neighborhood U of a and a unique holomorphic function g:U→R such that g(a)=b and (x,g(x)) is a solution of the equation f(x,y)=0 for all x in U.

In this case, since f(z) has a simple zero at z=0 and f'(0)≠0, by the Implicit Function Theorem, there exists an open neighborhood U of 0 and a unique holomorphic function h:U→C such that h(0)=0 and f(h(ϵ))=0 for all ϵ in U. Hence, fϵ(z) has a unique zero in |z|≤1.

Also, since f and g are holomorphic in a region containing the disc |z|≤1 and ϵ is continuous, it follows that fϵ is holomorphic in the same region. Thus, by the holomorphicity of fϵ and h, the mapping ϵ↦zϵ is continuous.

To learn more about the derivative, visit:

brainly.com/question/25324584

#SPJ4

The optimal values of these parameters are:

a. β₁ = 0

b. β₂ = 0

The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:

SSE = 382 + 681 + 382 + 18β1β2

Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.

Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0

Now, we need to find the partial derivative of SSE with respect to β1.

∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0

Therefore, we obtain the optimal value of β2 as 0.

Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0

Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.

Thus, the optimal values of β1 and β2 are 0 and 0, respectively.

Therefore, the answers are: a. β₁ = 0 b. β₂ = 0

Learn more about regression analysis at

https://brainly.com/question/31691955

#SPJ11

We can write every odd integer greater than four as the sum of integral power of 2 and a prime number. Therefore, there is no odd integer greater than four that cannot be written as the sum of integral power of 2 and a prime number.

Let the integer of interest be x. From provided details, x is an odd integer greater than 4. Therefore,

x = 2n + 1

where n ∈ N and n > 1

Also it cannot be written as the sum of an integral power of 2 and a prime number

2ᵃ + k ≠  x

where a is an integer and k is a prime number.

This prime cannot be 2 as x is odd.

Let us assume x = 2ᵃ + k.

2n + 1 = 2ᵃ + k

2n - 2ᵃ = k - 1

n - 2ᵃ⁻¹ = (k - 1)/ 2 6 8

n =  2ᵃ⁻¹ + (k -1)/2

This can be written as n =  2ᵃ + k

where a is an integer and k is 1, 3m or 3m - 1, where m ∈ {1, 2, 3, ...}

Considering n =  2ᵃ + 3m, thus n can be written as 3m + 1, when a = 0 and 3m + 2, when a = 1.

Considering n = 2ᵃ + 3m - 1, n can be written as 3m, when a = 0.

So in conclusion, n can be 3m, 3m + 1, 3m + 2, where m ∈ {1, 2, 3...}. So n can be any natural number. This does not contradict our assumption. So every odd integer greater than 4 that can be written as the sum of an integral power of 2 and a prime number.

To know more on integer

https://brainly.com/question/15483271

#SPJ4

gcd(40, 64) = 8, gcd(110, 68) = 2, and gcd(2021, 2023) = 1.
lcm(40, 64) = 320, lcm(35, 42) = 210, and lcm(2^2022 - 1, 2^2022 + 1) = 2^2022 - 1.
The value of 5152535455 modulo 7 is 4, and the value of 20192020202120222023 modulo 8 is 7.

To find the greatest common divisor (gcd) of two numbers, we determine the largest number that divides both of them without leaving a remainder. Thus, gcd(40, 64) = 8, gcd(110, 68) = 2, and gcd(2021, 2023) = 1.The least common multiple (lcm) of two numbers is the smallest number that is divisible by both of them. lcm(40, 64) = 320 because it is the smallest number that is divisible by both 40 and 64. Similarly, lcm(35, 42) = 210. The lcm of two consecutive odd numbers is their product. Hence, lcm(2^2022 - 1, 2^2022 + 1) = 2^2022 - 1.
To find the value of an expression modulo a number, we calculate the remainder when the expression is divided by that number. For the expression 5152535455, we can simplify the calculation by considering the congruence modulo 7. We can observe that each factor is congruent to 2 modulo 7, so their product is congruent to 2^5 ≡ 32 ≡ 4 modulo 7. Similarly, for the expression 20192020202120222023, each factor is congruent to 3 modulo 8. Multiplying them gives 3^5 ≡ 243 ≡ 7 modulo 8.
Therefore, the value of 5152535455 modulo 7 is 4, and the value of 20192020202120222023 modulo 8 is 7.

learn more about gcd here

https://brainly.com/question/30565465



#SPJ11

Answer:

14.73

Step-by-step explanation:

If this helped be sure to like and mark brainliest :)

For the two supplementary angles given, the value of x is 30. Two angles are called supplementary when their measures add up to 180 degrees.

If two angles are supplementary, their sum must equal 180 degrees. Supplementary angles are double of complementary angles.  So if m∠1=124° and

m∠2=(2x - 4)°, we can set up the equation:

124 + (2x - 4) = 180

Solving for x, we can isolate x by subtracting 124 from both sides:

2x - 4 = 56

Adding 4 to both sides:

2x = 60

Finally, dividing both sides by 2:

x = 30

So the value of x is 30

Learn more about angles here: brainly.com/question/25770607

#SPJ4

Answer:

C.) π/9

Step-by-step explanation:

√9/3 = 1

2π ≈ 6.28

The only value that is not between these two numbers is π/9 which is approximately 0.35.

Question 1

\(\sqrt{(3-8)^2 +(2-14)^2}=13\)

Question 2

\(\left(\frac{3+8}{2}, \frac{2+14}{2} \right)=(5.5, 8)\)

Question 3

\(M=\left(\frac{1+9}{2}, \frac{5+7}{2} \right)=(5, 6) \\ \\ N=\left(\frac{9+7}{2}, \frac{7+13}{2} \right)=(8, 10) \\ \\ MN=\sqrt{(8-5)^2 + (10-6)^2}=5\)