Find the area of the irregular figure.
6 in
7 in.
A = [? ]in.2
5 in.
12 in.
13 in
4 in
![Find The Area Of The Irregular Figure.6 In7 In.A = [? ]in.25 In.12 In.13 In4 In](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/OP0SKZQuKYeltq0DhEii0iLunPpXRojC.png)
Answers
Answer:
155 in
Step-by-step explanation:
Theres honestly no easy way to solve this except using a pencil and a notebook.
Anyways, heres how I did it:
6 times 7=42
17 times 5=85
7 times 4=28
42+85+28=155
Related Questions
A bag contains 3 gold marbles, 8 silver marbles, and 30 black marbles. Someone offers to play this game: You randomly select one marble from the bag. If it is gold, you win $3. If it is silver, you win $2. If it is black, you lose $1.
What is your expected value if you play this game?
Answers
Answer: To calculate the expected value, we need to multiply each possible outcome by its probability and then add up the results.
The probability of selecting a gold marble is 3/41, the probability of selecting a silver marble is 8/41, and the probability of selecting a black marble is 30/41.
The winnings/losses associated with each outcome are $3 for gold, $2 for silver, and -$1 for black.
Step-by-step explanation:
Therefore, the expected value can be calculated as follows:
(3/41) x $3 + (8/41) x $2 + (30/41) x (-$1)
= $0.073
The expected value is $0.073, which means that on average, you can expect to win $0.073 per game if you play this game many times.
Therefore, if you play this game, you can expect to win a small amount of money on average, but it is not a guaranteed win.
References:
Grinstead, C.M. and Snell, J.L. (2006). Introduction to Probability. American Mathematical Society.
"Expected Value," Investopedia, accessed May 14, 2023, https://www.investopedia.com/terms/e/expectedvalue.asp.
food is tight and you are given 98 oz. of bread every week. If you want to eat the same amount of bread every day, how many oz. should you eat each day?
Answers
Answer:
14 oz
Step-by-step explanation:
A week has 7 days and you need to ration your bread over them.
98 / 7 = 14
a company's sales in year 1 were $330,000 and in year 2 were $367,500. using year 1 as the base year, the percent change for year 2 compared to the base year is:
Answers
Percentage change in company's sales is 11%
What is percentage?
In arithmetic, a proportion may be a range or magnitude relation expressed as a fraction of a hundred. it's usually denoted victimisation the percentage sign, "%", d. A proportion may be a dimensionless number; it's no unit of measuring.
Main body:
According to the question:
company's sales in year 1 = $330,000
company's sales in year 2 =$367,500
Change = $ 367500 – 330000 = $ 37,500
Percentage change = $ 37500 / $ 330000 = 0.11
Percentage change = 11%
Hence ,Percentage change in company's sales is 11%.
to know more about , Percentage change , visit:
https://brainly.com/question/11712455
#SPJ1
50 Points! Multiple choice algebra graphing question. Which cube root function is represented by the graph? Photo attached. Thank you!

Answers
The cube root function represented by the graph is h(x) = ∛(x + 3) - 2.
Which cube root function is represented by the graph?The parent cube root function is f(x) = ∛x
If we translate the parent cube root function 3 units to the left, this means that we replace x with (x + 3) in the function.
This results in the new function g(x) = ∛(x + 3). So, for any input value of x, the output value of g(x) is the cube root of (x + 3).
Similarly, if we translate the parent cube root function 2 units down, this means that we subtract 2 from the function.
So, the new function h(x) = ∛(x + 3) - 2.
Read more about transformation at
https://brainly.com/question/1548871
#SPJ1
6. Determine the system of equations based on the following relationships and then solve
for the two integers.
a. Fourteen more than twice the first integer gives the second integer
b. The second integer increased by one is the square of the first integer
Answer: (-3,8) and (5,24)
Answers
The two pairs of integers that satisfy the given conditions are (-3, 8) and (5, 24).
To solve the system of equations, let's assign variables to the two integers. Let the first integer be represented by 'x' and the second integer by 'y'.
According to the given information:
a. Fourteen more than twice the first integer gives the second integer:
This can be expressed as: 2x + 14 = y
b. The second integer increased by one is the square of the first integer:
This can be expressed as: y + 1 = x^2
Now, we have a system of equations:
1) 2x + 14 = y
2) y + 1 = x^2
To solve this system, we can substitute the value of 'y' from equation 1) into equation 2):
2x + 14 + 1 = x^2
2x + 15 = x^2
Rearranging the equation, we have:
\(x^2 - 2x - 15 = 0\)
Factoring the quadratic equation, we get:
(x - 5)(x + 3) = 0
Setting each factor equal to zero:
x - 5 = 0 --> x = 5
x + 3 = 0 --> x = -3
Substituting the values of 'x' back into equation 1), we can find the corresponding values of 'y':
For x = 5:
2(5) + 14 = y
10 + 14 = y
y = 24
For x = -3:
2(-3) + 14 = y
-6 + 14 = y
y = 8
Therefore, the two pairs of integers that satisfy the given conditions are (-3, 8) and (5, 24).
for more such question on integers visit
https://brainly.com/question/929808
#SPJ8
If you have a statistical calculator or computer, use it to find the actual sample mean and sample standard deviation. Otherwise, use the values Σx = 2769 and Σx2 = 132,179 to compute the sample mean and sample standard deviation. (Round s to four decimal places.)
Answers
By using a statistical calculator, the actual sample mean and sample standard deviation are:
Actual sample mean = 46.1500.
Actual ample standard deviation = 8.6256.
How to calculate the sample mean for the set of data?In Mathematics and Geometry, the sample mean for any set of data can be calculated by using the following formula:
Mean = ∑x/(n - 1)
∑x represents the sum of all data values.(n - 1) represents the number of data contained in a sample.In Mathematics and Geometry, the sample standard deviation for any set of data can be calculated by using the following formula:
Standard deviation, δx = √(1/N × ∑(x - \(\bar{x}\))²)
x represents the observed values of a sample.\(\bar{x}\) is the mean value of the observations.N represents the total number of of observations.By using a statistical calculator, the actual sample mean and sample standard deviation are as follows;
Actual sample mean = 46.1500.
Actual ample standard deviation = 8.6256.
Read more on standard deviation here: brainly.com/question/14467769
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.


1. The proportion, p, of consumers who shop with coupons
is the ratio of the number, C, of consumers who use coupons
to the number, N, of consumers asked. Write an equation
for the proportion of consumers who shop with coupons.
Answers
The equation for the proportion, p, of consumers who shop with coupons is: p = C/N where C is the number of consumers who use coupons and N is the total number of consumers asked.
What is equation?An equation is a mathematical statement that indicates the equality of two expressions. It consists of two expressions separated by an equal sign (=). The expression on the left side of the equal sign is equivalent to the expression on the right side. Equations can have one or more variables, which are usually represented by letters such as x, y, or z. The goal in solving an equation is to determine the value(s) of the variable(s) that make the equation true. This involves manipulating the expressions on both sides of the equal sign using algebraic operations such as addition, subtraction, multiplication, and division, to isolate the variable on one side of the equation. Equations are used in many areas of mathematics and science to represent relationships between variables and to solve problems. They are also used in various fields such as engineering, physics, and economics to model real-world situations and make predictions based on mathematical analysis.
Here,
This equation represents the ratio of the number of consumers who use coupons to the total number of consumers. It is commonly used in statistics and market research to measure the prevalence of a certain behavior or preference among a population. By calculating the proportion of consumers who use coupons, businesses can make informed decisions about their pricing strategies, promotions, and advertising campaigns.
To know more about equation,
https://brainly.com/question/2228446
#SPJ9
When Makayla runs the 400 meter dash, her finishing times are normally distributed with a mean of 75 seconds and a standard deviation of 1.5 seconds. What is the probability that in a given race, her finishing time will be between 75 and 78 seconds, to the nearest thousandth?
Answers
The probability that in a given race, her finishing time will be between 75 and 78 seconds, using the normal distribution, is of:
0.4772 = 47.72%.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the obtained z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.The mean and the standard deviation for the finishing times are given as follows:
\(\mu = 75, \sigma = 1.5\)
The probability that in a given race, her finishing time will be between 75 and 78 seconds, is the p-value of Z when X = 78 subtracted by the p-value of Z when X = 75, hence:
X = 78:
Z = (78 - 75)/1.5
Z = 2
Z = 2 has a p-value of 0.9772.
X = 75:
Z = (75 - 75)/1.5
Z = 0
Z = 0 has a p-value of 0.5.
0.9772 - 0.5 = 0.4772 = 47.72%.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
The conditional statement below is true. If possible, write the biconditional statement.
If 2x = 18, then x = 9.
Answers
The biconditional statement for the given conditional statement would be:
2x = 18 if and only if x = 9.
The given conditional statement "If 2x = 18, then x = 9" can be represented symbolically as p → q, where p represents the statement "2x = 18" and q represents the statement "x = 9".
To form the biconditional statement, we need to determine if the converse of the conditional statement is also true. The converse of the original statement is "If x = 9, then 2x = 18". Let's evaluate the converse statement.
If x = 9, then substituting this value into the equation 2x = 18 gives us 2(9) = 18, which is indeed true. Therefore, the converse of the original statement is true.
Based on this, we can write the biconditional statement:
2x = 18 if and only if x = 9.
The biconditional statement implies that if 2x is equal to 18, then x must be equal to 9, and conversely, if x is equal to 9, then 2x is equal to 18. The biconditional statement asserts the equivalence between the two statements, indicating that they always hold true together.
In summary, the biconditional statement is a concise way of expressing that 2x = 18 if and only if x = 9, capturing the mutual implication between the two statements.
for such more question on conditional statement
https://brainly.com/question/27839142
#SPJ8
please answer quickly!!!

Answers
Answer:
\(c=20\)
Step-by-step explanation:
The diagonals of a rectangle always bisect each other. Therefore, we can set \(QT=ST\):
\(c=4c-60,\\-3c=-60,\\c=\fbox{20}\)
Please help me with this proof.

Answers
Answer:
See below
Step-by-step explanation:
For the second step, \(\angle T\cong\angle R\) by Alternate Interior Angles. The rest of the steps appear to be correct.
Of the respondents, 514 replied that America is doing about the right amount. What is the 95 % confidence interval for the proportion of all American adults who feel that America is doing about the right amount to protect the environment. g
Answers
Complete Question
In 2015 as part of the General Social Survey, 1127 randomly selected American adults responded to this question: “Some countries are doing more to protect the environment than other countries. In general, do you think that America is doing more than enough, about the right amount, or too little?” Of the respondents, 514 replied that America is doing about the right amount. What is the 95 % confidence interval for the proportion of all American adults who feel that America is doing about the right amount to protect the environment.
Answer:
The 95% confidence interval is \( 0.427 < p < 0.4852 \)
Step-by-step explanation:
From the question we are told that
The sample size is n = 1127
The number that America is doing the about the right amount is k = 514
Generally the sample proportion of the number that say america is doing about the right amount is mathematically represented as
\(\^ p = \frac{k}{n}\)
=> \(\^ p = \frac{514 }{ 1127}\)
=> \(\^ p = 0.4561\)
From the question we are told the confidence level is 95% , hence the level of significance is
\(\alpha = (100 - 95 ) \%\)
=> \(\alpha = 0.05\)
Generally from the normal distribution table the critical value of \(\frac{\alpha }{2}\) is
\(Z_{\frac{\alpha }{2} } = 1.96\)
Generally the margin of error is mathematically represented as
\(E = Z_{\frac{\alpha }{2} } * \sqrt{\frac{\^ p (1- \^ p)}{n} } \)
=> \(E = 1.96 * \sqrt{\frac{ 0.4561 (1- 0.4561)}{1127} } \)
=> \(E = 0.0291 \)
Generally 95% confidence interval is mathematically represented as
\(\^ p -E < p < \^ p +E\)
=> \( 0.4561 -0.0291 < p < 0.4561 +0.0291 \)
=> \( 0.427 < p < 0.4852 \)
Statistical data of breakdowns of computer XXX show that the duration for trouble-free operation of the machine can be described as a gamma distribution with a mean of 40 days and a standard deviation of 10 days. The computer is occasionally taken out for maintenance in order to insure operational condition at any time with a 95% probability.
1. How often should the computer be scheduled for maintenance? Should it be shorter or longer than the mean of 40 days?
2. Three XXX computers were acquired at the same time by an engineering consulting firm. The computers are operating under the same environment, workload, and regular maintenance schedule. The breakdown times between the computers, however, may be assumed to be statistically independent. What is the probability that at least one of the three machines will break down within the first scheduled maintenance time?
Answers
1. In this case, we want the reliability to be 95%, so the probability of not breaking down is 0.95.
2. Probability of no breakdowns = (reliability of a single machine)^3. Probability of at least one breakdown = 1 - Probability of no breakdowns
1. To determine how often the computer should be scheduled for maintenance, we need to consider the reliability and the desired level of operational condition. Since the duration for trouble-free operation follows a gamma distribution with a mean of 40 days, this means that, on average, the computer can operate for 40 days before a breakdown occurs.
To ensure operational condition with a 95% probability, we can calculate the maintenance interval using the concept of reliability. The reliability represents the probability that the machine will not break down within a certain time period. In this case, we want the reliability to be 95%, so the probability of not breaking down is 0.95.
Using the gamma distribution parameters, we can find the corresponding reliability for a specific time duration. By setting the reliability equation equal to 0.95 and solving for time, we can find the maintenance interval:
reliability = 0.95
time = maintenance interval
Using reliability and the gamma distribution parameters, we can calculate the maintenance interval.
2. To calculate the probability that at least one of the three machines will break down within the first scheduled maintenance time, we can use the complementary probability approach.
The probability that none of the machines will break down within the first scheduled maintenance time is given by the reliability of a single machine raised to the power of the number of machines:
Probability of no breakdowns = (reliability of a single machine)^3
Since the breakdown times between the machines are statistically independent, we can assume that the reliability of each machine is the same. Therefore, we can use the reliability calculated in the first part and substitute it into the formula:
Probability of at least one breakdown = 1 - Probability of no breakdowns
By calculating this expression, we can determine the probability that at least one of the three machines will break down within the first scheduled maintenance time.
For more such questions on Probability
https://brainly.com/question/23286309
#SPJ8
For question 30, state the domain and range of the function.

Answers
Step-by-step explanation:
normally a simple expression in x has no natural limitations.
but for fractions we have to pay attention, because we have to avoid results like .../0, as they are undefined.
so, 4x + 1 has no limitations, but x² - 1 must never be 0.
the only "bad cases" are
x² - 1 = 0
x² = 1
x = ±1
therefore, the domain (the definition of the valid values for x) is
x € R, x <> -1 and x <> 1
the range (the definition of valid values for y) is then any value between -infinity and +infinity.
simply because around x=-1 and x=+1 the tendency goes against - and + infinity.
i need help can someone help me right now!!!!!!

Answers
(a) | BD | bisects | AC | (reason : Given)
(b) |AD| ≅ |CD| (reason: |BD| is the perpendicular bisector of segment AC).
(c) ∠ABD ≅ ∠CBD (reason: | BD | bisects angle ABC)
(d) ∠A ≅ ∠ C (reason: complementary angles of a right triangle)
What is the complete proof of the congruent angles?Congruent angles are the angles that have equal measure. So all the angles that have equal measure will be called congruent angles.
From the first statement, we will complete the flow chart as follows;
line BD bisects line AC (reason : Given)
line AD is congruent to line CD (reason: line BD is the perpendicular bisector of segment AC)
Angle ABD is congruent to angle CBD (reason: line BD bisects angle ABC)
Angle A is congruent to angle C (reason: angle ABD = angle CBD, and both triangles ABD and CBD are right triangles).
Learn more about congruent angles here: https://brainly.com/question/28262429
#SPJ1
the value of the power 4⁴=
Answers
Answer:
256
Step-by-step explanation:
4⁴
= 4 × 4 × 4 × 4
= 16 × 16
= 256
Airline travelers should be ready to be more flexible as airlines once again cancel thousands of flights this summer. The Coalition for Airline Passengers Rights, Health, and Safety averages 400 calls a day to help stranded travelers deal with airlines (seattlepi.com, July 10, 2008). Suppose the hotline is staffed for 16 hours a day. a. Calculate the average number of calls in a one-hour interval; 30-minute interval; 15-minute interval. (Round your answers to 2 decimal places.) Interval Average Number of Calls 60-minute 30-minute 15-minute b. What is the probability of exactly 6 calls in a 15-minute interval? (Round your intermediate calculations and final answer to 4 decimal places.) Probability c. What is the probability of no calls in a 15-minute interval? (Round your intermediate calculations and final answer to 4 decimal places.) Probability d. What is the probability of at least two calls in a 15-minute interval? (Round your intermediate calculations and final answer to 4 decimal places.) Probability
Answers
The Coalition for Airline Passengers Rights, Health, and Safety averages 400 calls a day to help stranded travelers deal with airlines. The hotline is staffed for 16 hours a day.
To calculate the average number of calls in different time intervals and the probability of different events related to these calls.
Part 1:
a. 60-minute interval average number of calls: 400/16 = 25 calls
30-minute interval average number of calls: 25/2 = 12.5 calls
15-minute interval average number of calls: 12.5/2 = 6.25 calls
Part 2:
b. To find the probability of exactly 6 calls in a 15-minute interval, we can use the Poisson distribution formula. Let's assume that the average number of calls in a 15-minute interval is 6.25. Then, the probability of exactly 6 calls in a 15-minute interval is:
P(6 calls) = (e^-6.25)*(6.25^6)/6! = 0.0686
c. To find the probability of no calls in a 15-minute interval, we can use the Poisson distribution formula. Let's assume that the average number of calls in a 15-minute interval is 6.25. Then, the probability of no calls in a 15-minute interval is:
P(0 calls) = e^-6.25 = 0.0047
d. To find the probability of at least two calls in a 15-minute interval, we can use the cumulative distribution function of the Poisson distribution. Let's assume that the average number of calls in a 15-minute interval is 6.25. Then, the probability of at least two calls in a 15-minute interval is:
P(X >= 2) = 1 - P(0 calls) - P(1 call) = 1 - 0.0047 - (e^-6.25)*(6.25^1)/1! = 0.9906
Thus, the average number of calls in a 60-minute interval is 25, in a 30-minute interval is 12.5, and in a 15-minute interval is 6.25. The probability of exactly 6 calls in a 15-minute interval is 0.0686, the probability of no calls in a 15-minute interval is 0.0047, and the probability of at least two calls in a 15-minute interval is 0.9906.
Learn more about Probability here brainly.com/question/11234923
#SPJ4
The mapping diagram above ( does NOT represent or represent) a function since ( for each number or there is one number) in ( set A the out put, set B the input, set A the input, set B the output) where there ( is no mapping, is only one mapping, are multiple mapping), ( from set A the input, from set A output, to set B the output, to set B the input).

Answers
Remember that
The data set is a function if every element of the domain corresponds to exactly one element of the range
In this problem
the relationship between A and B does not represent a function, because
for one value of set A, there are two values of set B
example
set A ----> -4 -----------> correspond 3 and 2 values of set B
therefore
the answers are
does NOT represent a function
there is one number in set A
where there are multiple mapping
from set A the input, to set B the output
Solve y = ax² + c for x.
O x
x= ± √ay-c
O
O
x = ±₁
X=
X=
у-с
a
y
y + c
a

Answers
In the quadratic equation y = a\(x^{2}\) + c ,the value of x = ± \(\sqrt \frac{y-c}{a}\)
A quadratic equation is any equation containing one term wherein the unknown is squared and no term wherein it's far raised to a higher power.
A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax2 + bx + c = 0, in which a and b are the coefficients, x is the variable, and c is the constant term.
To find the value of x
Assuming \(a\neq o\)
First, subtract c from both the sides to get:
\(y-c=ax^{2}\)
then, divide both sides by \(a\) and transpose to get:
\(x^{2} =\frac{y-c}{a}\)
So, \(x\) must be a square root of \(\frac{y-c}{a}\) and we can deduce:
\(x=\) ± \(\sqrt \frac{y-c}{a}\)
Learn more about quadratic equations here brainly.com/question/1214333
#SPJ9
An urn contains 25 red marbles, 27 blue marbles, and 36 yellow marbles. One marble is to be chosen from the urn without looking. What is the probability of choosing a red marble?
Answers
Answer:
25/88
Step-by-step explanation:
25 red marbles, 27 blue marbles, and 36 yellow marbles. = 88 marbles
P(red) = number of red/total
= 25/88
Answer:
Dear user,
Answer to your query is provided below
Probability of choosing a red marble is 0.28 or (25/88)
Step-by-step explanation:
Total number of marbles = 88
Number of red marbles = 25
Probability = 25/88
Bianca can walk 5/6 of miles 1/3 of an hour. What is her walking speed,in miles per hours?
Answers
Answer:
Step-by-step explanation:
To find Bianca's walking speed, we need to divide the distance she walks by the time it takes her to walk that distance. We can do this by converting both the distance and time to the same unit of measure.
Since 1 hour is equal to 60 minutes, 1/3 of an hour is equal to 1/3 * 60 minutes = 20 minutes. Now that we have the distance in miles and the time in minutes, we can divide the distance by the time to find Bianca's walking speed.
5/6 of a mile is equal to 5/6 * 1 mile = 0.83 miles. So, Bianca's walking speed is 0.83 miles / 20 minutes = 0.0415 miles per minute. To convert this to miles per hour, we can multiply by the conversion factor of 60 minutes per hour. This gives us a walking speed of 0.0415 miles/minute * 60 minutes/hour = 2.49 miles per hour. So, Bianca's walking speed is 2.49 miles per hour.
Suppose that the lifetimes of a certain kind of light bulb are normally distributed with a standard deviation of 110 hours. If exactly 90% of the bulbs die before 930 hours, find the mean lifetime of the bulbs. Carry your intermediate computations to at least four decimal places.
Answers
Answer:
sorry bro
Step-by-step explanation:
i really need the points
Which number does not belong with the other three? Please explain

Answers
The number that does not belong with the other three is D. 10 x 9.2 ⁻¹³
Why is the number different from the others ?With the first three numbers, the base of the exponential that is being multiplied by the first number is 10. These numbers are:
2 . 8 x 10 ¹⁵4. 3 x 10 ⁻³⁰1. 05 x 10 ²⁸With the last number however, we see that the base of the exponential is 9. 2 and not 10 like the others. This is why 10 x 9 . 2 ⁻¹³ does not belong with the rest.
Find out more on numbers at https://brainly.com/question/28358811
#SPJ1
Instructions: Use the ratio of a 30-60-90 triangle to solve for the variables. Leave your answers as radicals in simplest form.
If you are using a screen-reader, please consult your instructor for assistance.
x=
y=
Answers
Using the ratio of the sides, we have:$x\sqrt{3} = 12\sqrt{3}$ (opposite the $60^{\circ}$ angle is 12$\sqrt{3}$)$x = 2\sqrt{3}\cdot6$ (the hypotenuse is $2x = 12\sqrt{3}$)Simplifying, we have:$x = 12\sqrt{3}$. Therefore $x=y=12\sqrt{3}$, which is our answer
In a 30-60-90 triangle, the sides have the ratio of $1: \sqrt{3}: 2$. Let's apply this to solve for the variables in the given problem.
Instructions: Use the ratio of a 30-60-90 triangle to solve for the variables. Leave your answers as radicals in simplest form. x=y=Let's first find the ratio of the sides in a 30-60-90 triangle.
Since the hypotenuse is always twice as long as the shorter leg, we can let $x$ be the shorter leg and $2x$ be the hypotenuse.
Thus, we have: Shorter leg: $x$Opposite the $60^{\circ}$ angle: $x\sqrt{3}$ Hypotenuse: $2x$
Now, let's apply this ratio to solve for the variables in the given problem. We know that $x = y$ since they are equal in the problem.
Using the ratio of the sides, we have:$x\sqrt{3} = 12\sqrt{3}$ (opposite the $60^{\circ}$ angle is 12$\sqrt{3}$)$x = 2\sqrt{3}\cdot6$ (the hypotenuse is $2x = 12\sqrt{3}$)Simplifying, we have:$x = 12\sqrt{3}$
Therefore, $x=y=12\sqrt{3}$, which is our answer.
For more such questions on ratio of the sides
https://brainly.com/question/31529028
#SPJ8
The Following to wait table shows the number of student of the school who have a cell phone and or part-time job:
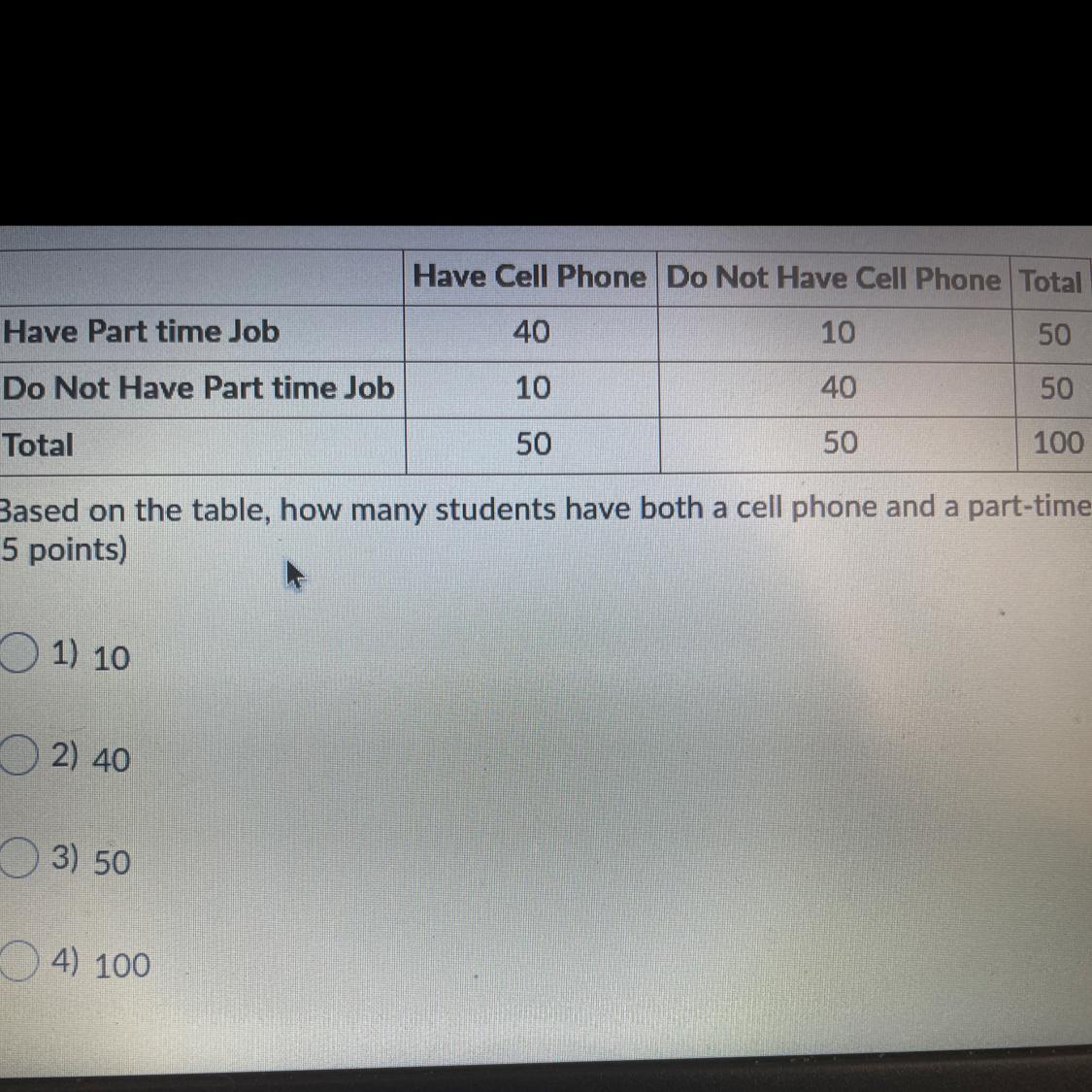
Answers
Explanation
in the column we have
-have cell phones
-do not have cell phones
-total
and
in the other side.
-have a part time job
-do not have part time job,
so to know the number of students whoh fit both conditions ( have a cell phone and have a part time job) we need to find the cell where both intersect each other
hence, the answer is
\(2)40\)I hope this helps you

Expand. Your answer should be a polynomial in standard form. (- 2h + 9)(9h - 2) = (9h - 2) =

Answers
Answer:18h^2+85h-18
Step-by-step explanation:
Answer:
−18h^2+85h−18
Step-by-step explanation:
The hourly median power (in decibels) of received radio signals transmitted between two cities
follows a lognormal distribution with parameter values u = 3.5 and o2 = 1.22.
(5 points) What is the 90th percentile of this distribution?
(5 points) What is the probability that received power for one of these radio signals is
less than 150 decibels?
(5 point) Consider a random sample of 10 radio signals. What is the probability that for
6 of these signals, the received power is less than 150 decibels?
Answers
Using the lognormal and the binomial distributions, it is found that:
The 90th percentile of this distribution is of 136 dB.There is a 0.9147 = 91.47% probability that received power for one of these radio signals is less than 150 decibels.There is a 0.0065 = 0.65% probability that for 6 of these signals, the received power is less than 150 decibels.In a lognormal distribution with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{\ln{X} - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X.In this problem:
The mean is of \(\mu = 3.5\).The standard deviation is of \(\sigma = \sqrt{1.22}\)Question 1:
The 90th percentile is X when Z has a p-value of 0.9, hence X when Z = 1.28.
\(Z = \frac{\ln{X} - \mu}{\sigma}\)
\(1.28 = \frac{\ln{X} - 3.5}{\sqrt{1.22}}\)
\(\ln{X} - 3.5 = 1.28\sqrt{1.22}\)
\(\ln{X} = 1.28\sqrt{1.22} + 3.5\)
\(e^{\ln{X}} = e^{1.28\sqrt{1.22} + 3.5}\)
\(X = 136\)
The 90th percentile of this distribution is of 136 dB.
Question 2:
The probability is the p-value of Z when X = 150, hence:
\(Z = \frac{\ln{X} - \mu}{\sigma}\)
\(Z = \frac{\ln{150} - 3.5}{\sqrt{1.22}}\)
\(Z = 1.37\)
\(Z = 1.37\) has a p-value of 0.9147.
There is a 0.9147 = 91.47% probability that received power for one of these radio signals is less than 150 decibels.
Question 3:
10 signals, hence, the binomial distribution is used.
Binomial probability distribution
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes. n is the number of trials. p is the probability of a success on a single trial.For this problem, we have that \(p = 0.9147, n = 10\), and we want to find P(X = 6), then:
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 6) = C_{10,6}.(0.9147)^{6}.(0.0853)^{4} = 0.0065\)
There is a 0.0065 = 0.65% probability that for 6 of these signals, the received power is less than 150 decibels.
You can learn more about the binomial distribution at https://brainly.com/question/24863377
In ΔQRS, the measure of ∠S=90°, SQ = 13 feet, and QR = 59 feet. Find the measure of ∠R to the nearest tenth of a degree.
Answers
Answer:12.7
Step-by-step explanation:
Answer:
it's 12.7 on delta math
Step-by-step explanation:
Anyone?? Help????
Please!!!

Answers
Answer:
625 (answer A)
Step-by-step explanation:
Sorry for no explanation I can't explain stuff I just do it.
HELP! SAS SSA ASA need in right places please

Answers
1-SSS
2-ASA
3-None