Find the angle measure indicated. Assume that lines which appear to betangent are tangent.114?

Answers
EXPLANATION
Applying the Angles in Circles Theorem we can assevere that the measure of the unknown angles is given by the difference between 360 (By the Sum of Interior Angles of a Quadrilateral Theorem) and the angle 114 with both right angles.
? = 360 -114 - 90 - 90
? = 66 degrees
The answer is 66 degrees
Related Questions
you and your friend are playing a number-guessing game. You ask your friend to think of a positive number, square the number, multiply the results by 2 and then add 3. your friend's final answer is 53.
Answers
Answer:
It is 5....
Step-by-step explanation:
Solve each system by substitution

Answers
-x - y = 9
x = -y - 9
-3(-y - 9) + y = 3
4y + 27 = 3
y = -6
x = -(-6) - 9
x = 6 - 9
x = -3
there are 750 spectator in the stadium of which 420 are women and the rest are men
Answers
Complete Question:
There are 750 spectator in the stadium of which 420 are women and the rest are men. What percent of the spectators are women?
Answer:
Percentage = 56%
Step-by-step explanation:
Given the following data;
Total number of people = 750
Number of women = 420
To find the percentage of women;
First of all, we would determine the number of male spectators (men);
Number of men = Total number of people - Number of women
Number of men = 750 - 420
Number of men = 330
Next, we find the percentage of women;
\( Percentage = \frac {420}{750} * 100 \)
\( Percentage = \frac {42}{75} * 100 \)
\( Percentage = 0.56 * 100 \)
Percentage = 56%
Therefore, the percentage of the spectators that are women is 56%.
A number cube is rolled three times. An outcome is represented by a string of the sort OEE (meaning an odd number on the first roll, an even number on the second roll, and an even number on the third roll). The outcomes are listed in the table below. Note that each outcome has the same probability.

Answers
The probability of occurrence for the events A, B and C is; 1/4.
What is the probability of occurrence of.the described events?For the first event A in which case, there's no odd number on the first two rolls, the possible events are; EEE and EEO. Consequently, the required probability is;
Event A = 2/8 = 1/4.
For the event B in which case, there's an even number on both the first and last rolls; the possible events are; EEE and EOE. Consequently, the required probability is;
Event B = 2/8 = 1/4.
For the event C in which case, there's an odd number on each of the first two rolls; the possible events are; OOO and OOE. Consequently, the required probability is;
Event C = 2/8 = 1/4.
Read more on probability;
https://brainly.com/question/251701
#SPJ1
Question 4
What is the solution of the equation? Prove your answer to be correct.
1/3(6z + 7.2) = 0.5(8z + 2) - 0.4
a. z = 0.8
b. z = 0.9
c. Z = 2.8
d. z = 3.6
Answers
The value of z in the equation 1/3(6z + 7.2) = 0.5(8z + 2) - 0.4 is z=0.9
How to solve the equation?
Remove parentheses from each side of the equation and combine similar phrases to make it simpler.To separate the variable term on one side of the equation, use addition or subtraction.To find the variable, use division or multiplication.The algebraic expression should often take one of the following forms: addition, subtraction, multiplication, or division.Bring the variable to the left and the remaining values to the right to determine the value of x. To determine the outcome, simplify the values.1/3(6z + 7.2) = 0.5(8z +2) -0.4
(6/3)z + 7.2/3 = (8/2)z + 2/2 - 0.4
2z + 2.4 = 4z + 1 - 0.4
2z - 4z = 0.6 - 2.4
-2z = -1.8
z= 0.9
Hence, the value of z in the equation 1/3(6z + 7.2) = 0.5(8z + 2) - 0.4 is z=0.9
To know more about equation check the below link:
https://brainly.com/question/26310043
#SPJ1
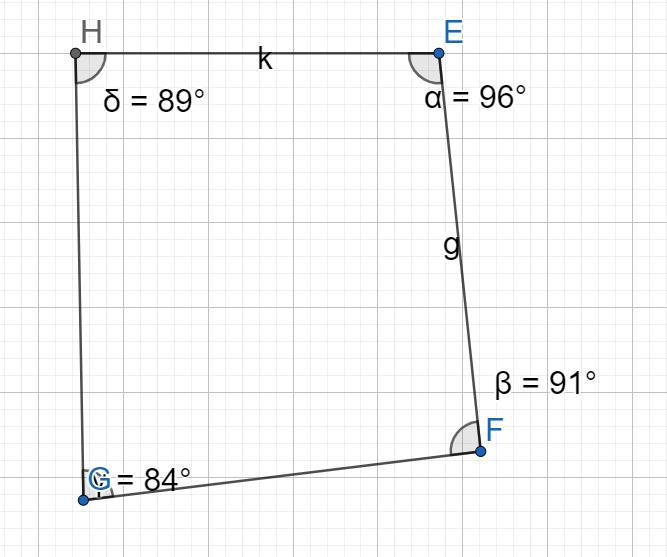
Choose ALL answers that describe the polygon EFGH ifmZE = 96°,m2F = 91°, mZG = 89°, m_H = 84°, and EF || GH.
Answers
Explanation
Lets first graph the figure:
A figure cannot be constructed with the given conditions because the alternate internal angles would not correspond in the parallels.
But assuming it can, it must be a trapezoid and therefore a quadrilateral.
Answer
Trapezoid.
Quadrilateral.
help me please!!!
..

Answers
Step-by-step explanation:
HERE,
as,it is a right angle triangle,
x=\(\tt{\sqrt{8^2+6^2} }\)
\(\tt{ x=\sqrt{64+36} }\)
\(\tt{ x=\sqrt{100} }\)
\(\tt{x=10km. }\)
The perimeter of a rectangle is 202 the length is 26 more than 4 times the width find the dimensions
Answers
Answer:
Width = xLength = 26 + 4xPerimeter
\(202 = x + x + 26 + 4x + 26 + 4x\\202-26-26=10x\\150=10x\\x=15\)
Therefore, the dimensions are
Width = x = 15Length = 26 + 4x = 26 + 4(15) = 86Complete the proportion of these similar figures.
Answers
Where are the figures, can you upload a Pic of the figures so that I can answer your question
Simplify and solve the equation

Answers
Answer:
y=6
Step-by-step explanation:
y+6 3
----- = ----
8 2
2(y+6)=8(3)
2y+12=24
2y=24-12
2y = 12
---- ----
2 2
therefore y=6
Answer:
it will be 6 im 100%
Step-by-step explanation:
y=6
Hunter surveyed 200 of the students in his school bout there favorite color. 66 student said their favorite color was blue. What % of the surveyed student said there color was blue?
Answers
___ ÷ 8 + 9 = 16
Find missing number
Answers
Answer:
56
Step-by-step explanation:
Answer: 56
Step-by-step explanation:
First, you can set up the problem algebraically like this:
\(\frac{x}{8}+9=16\)
Then, subtract 9 from both sides:
\(\frac{x}{8}+9=16\)
-9 -9
\(\frac{x}{8}=7\)
Finally, multiply both sides by 8 and you get:
\(\frac{x}{8}=7\)
×8 ×8
\(x=56\)
Therefore, the missing number is 56.
I hope this helps!
Human visual inspection of solder joints on printed circuit boards can be very subjective. Part of the problem stems from the numerous types of solder defects (e.g., pad non-wetting, knee visibility, voids) and even the degree to which a joint possesses one or more of these defects. Consequently, even highly trained inspectors can disagree on the disposition of a particular joint. In one batch of 10,000 joints, inspector A found742that were judged defective, inspector B found745such joints, and1145of the joints were judged defective by at least one of the inspectors. Suppose that one of the 10,000 joints is randomly selected.
(a) What is the probability that the selected joint was judged to be defective by neither of the two inspectors? (Enter your answer to four decimal places.)
(b) What is the probability that the selected joint was judged to be defective by inspector B but not by inspector A? (Enter your answer to four decimal places.)
Answers
Answer:
a
The probability that the selected joint was judged to be defective by neither of the two inspectors is \(P(A' n B' ) = 0.8855\)
b
The probability that the selected joint was judged to be defective by inspector B but not by inspector A is \(P(A' n B) =0.0403\)
Step-by-step explanation:
From the question we are told that
The sample size is \(n_s = 10000\)
The number of outcome for inspector A is \(n__{A}} = 742\)
The number of outcome for inspector B is \(n__{B}} = 745\)
The number of joints judged defective by both inspector is \(n(A u B) = 1145\)
The the probability that the selected joint was judged to be defective by neither of the two inspectors is mathematically represented as
\(P(A' n B' ) = 1 - P(A u B)\)
Now
\(P(A\ u \ B) = \frac{n(Au B)}{n_s }\)
substituting values
\(P(A\ u \ B) = \frac{1145}{ 10 000 }\)
So
\(P(A' n B' ) = 1 - \frac{1145}{10 000}\)
\(P(A' n B' ) = 0.8855\)
the probability that the selected joint was judged to be defective by inspector B but not by inspector A is mathematically represented as
\(P(A' n B) = P(A \ u \ B) -P(A)\)
Now
\(P(A) = \frac{n__{A}}{n_s}\)
substituting values
\(P(A) = \frac{742}{10 000}\)
So
\(P(A' n B) = \frac{1145}{10 000} - \frac{742}{10 000}\)
\(P(A' n B) =0.0403\)
NEED HELP ASAP 25 POINTS HELP A GIRL GET HER GEOMETRY GRADE UP

Answers
The angle measure of x, y and z are 104, 76 and 104 degrees respectively
Determining the angles in a parallelogramThe given. figure is a parallelogram with 4 interior angles. In a parallelogram, the sum of its adjacent angle is 180 degrees and its opposite angles are equal.
<A = <C
x = 104 degrees
For the measure of y:
x + y = 180
104 + y = 180
y = 180 - 104
y = 76 degrees
Since the sum of angles on a straight line is 180 degrees, hence;
y + z = 180
76 + z = 180
z = 104 degrees
Hence the measure of x, y and z are 104, 76 and 104 degrees respectively
Learn more on parallelograms here: https://brainly.com/question/14285697
#SPJ1
Consider two lines. Line A is given by the function f(x) = 4x - 9, while Line B contains the points (0,5) and (2.12).
Which statement is true?
A) Line A and Line B have the same slope.
B) Line A has a greater slope than Line B C)Line B has a greater slope than Line A.
D) Line A slope is less than the slope of Line B.
Answers
Answer:
line D
Step-by-step explanation:
ooo
Answer: B
Step-by-step explanation:
Given the points R(-8,2) and S(-1,6), use the distance formula to find RS.
Round your answer to the nearest hundredth.
Answers
Write a polynomial to this

Answers
The polynomial of degree 3 in factored form is calculated and of the form: y = x(x + 3)(x - 10) + 210
How to write the polynomialInformation given in the question include
degree 3
leading coefficient 1
x intercept (10, 0) and (-3, 0)
y intercept (0, -210)
The polynomial is written starting from the x intercept
x = 10, (x - 10)
x = -3, (x + 3)
(x + 10)(x - 10)
y = (x + 3)(x - 10)
for a polynomial of degree three and leading coefficient 1
y = x(x + 3)(x - 10)
for a y intercept (0, -210)
y = x(x + 3)(x - 10)
- 210 = 0
y = x(x + 3)(x - 10) + 210
The factored form of the polynomial is y = x(x + 3)(x - 10) + 210
Learn more about polynomial at:
https://brainly.com/question/4142886
#SPJ1
Use what you know about intersecting lines to label the missing and
picture below.
35°
X
type of angle pair:
zoom in
X =
OManeuvering the Middle LLC, 2016, 2022

Answers
Answer:
x = 145
Step-by-step explanation:
x and 35° lie on a straight line and are supplementary angles , sum to 180°
x + 35 = 180 ( subtract 35 from both sides )
x = 145
solve for a, 1/3 + a = 5/4
Answers
Answer:
\(a = \frac{11}{12}\)
Step-by-step explanation:
\(a = \frac{5}{4} - \frac{1}{3}\)
\(a = \frac{11}{12}\)
Answer:
\( \frac{1}{3} + a = \frac{5}{4} \)
\(a = \frac{5}{4} - \frac{1}{3} \)
\(a = \frac{15 - 4}{12} \)
\(a = \frac{11}{12} \)
You start at (0,-4). You move left 1 unit and right 4 units. where do you end?
Answers
If you start at (0,-4) and you move left 1 unit and right 4 units, you end at (3, -4)
Calculating the endpoint of the pointFrom the question, we have the following parameters that can be used in our computation:
Start = (0, -4)
Also, we have
You move left 1 unit and right 4 units
Mathematically, this can be expressed as
(x, y) = (x - 1 + 4, y)
Substitute the known values in the above equation, so, we have the following representation
Endpoint = (0 - 1 + 4, -4)
Evaluate the expression
Endpoint = (3, -4)
Hence, the endpoint is (3, -4)
Read more about transformation at
https://brainly.com/question/27224272
#SPJ1
need help asap please
Answers
Ali's strategy is essentially the same as Mary's strategy. Both strategies estimate the HST as 15% of the price. However, Mary's strategy involves taking half of 10% of the price.
How to explain the strategies usedMary suggests estimating the HST in Ontario as finding 10% of the price, taking half of this answer and adding the two. Ali proposes finding 10% of the price, then 5% of the price and adding the two answers.
Their strategies differ in the way they approach finding the estimate, but both methods can be used to arrive at the same result.
Learn more about price on
https://brainly.com/question/1153322
#SPJ1
The HST in Ontario is 13%, which can be estimated using 15%. Mary tells Ali that it can be estimated as: find 10% of the price, take a half of this answer and add the two. Ali tells Mary that he thinks they should find 10% of the price, then 5% of the price and add the two answers. Compare their strategies.
Help me thank y very much

Answers
Answer: 1/2
Step-by-step explanation:
Use rise over run. Up 1, over 2.
And so on. Find nice points on the graph to practice slope with!
create a system of equations that represents the situation below

Answers
Variables
• L: length of the rectangular garden, in ft
,• W: width of the rectangular garden, in ft
The perimeter of a rectangle is computed as follows:
\(P=2W+2L\)The perimeter of the rectangular garden is 72 ft, then:
\(72=2W+2L\text{ (eq. 1)}\)The width is 8 ft more than twice the length, then:
\(W=8+2L\text{ (eq. 2)}\)Equations 1 and 2 compose the system of equations.
50 PONTS
Complete the following statements:
< A corresponds to <
< B corresponds to <
< C corresponds to <
Side CA corresponds to side?
Side BC corresponds to side?
Side AB corresponds to side?

Answers
Answer:
Step-by-step explanation:
1. j
2. k
3. L
4. Lj
5. kL
6. jk
Expressed in simplest a + bi form, (7-3i) + (x - 2i)² - (4i + 2x²) is
Answers
Therefore, the expression (7-3i) + (x - 2i)² - (4i + 2x²) in the simplest a + bi form is: -2x² - 1 - (4x + 7i)
What are the different forms of linear equation?Linear Equation General Form Example
Slope intercept form y = mx + b y + 2x = 3
Point–slope form y – y1 = m(x – x1 ) y – 3 = 6(x – 2)
General Form Ax + By + C = 0 2x + 3y – 6 = 0
Intercept form x/a + y/b = 1 x/2 + y/3 = 1
As a Function f(x) instead of y f(x) = x + C f(x) = x + 3
The Identity Function f(x) = x f(x) = 3x
Constant Functions f(x) = C f(x) = 6
Let's start by expanding the square term (x - 2i)² using the formula for (a + b)²:
(x - 2i)² = x² - 4xi + 4i²
Note that i² = -1, so we can simplify this expression to:
(x - 2i)² = x² - 4xi - 4
Substituting this expression and the given values into the original expression, we get:
(7 - 3i) + (x² - 4xi - 4) - (4i + 2x²)
Grouping the real and imaginary terms, we get:
(7 - 4 - 2x²) + (-3i - 4i - 4x) + (x²)
Simplifying the real part, we get:
-2x² - 1
Simplifying the imaginary part, we get:
-7i - 4x
Learn more about Linear equations here:
brainly.com/question/11897796
#SPJ1
At a certain conference, three sessions were held at the same time period. The number of male and female
attendees at the three sessions was recorded, and the results are summarized below:
Male
Female
Session 1
Male 12
Female 8
Session 2
Male 18
Female 9
Session 3
Male 17
Female 5
a.) How many men attended the sessions?
b.) How many people attended Session 3?
c.) What is the sample size?
d.) If a random person is selected, what is the probability (to four decimal places) that the person is male?
e.) If a random person is selected, what is the probability (to four decimal places) that the person attended Session
3?
f.) If a random person is selected, what is the probability (to four decimal places) that the person is male and
attended Session 3?
Make sure to work out each problem not a multiple choice!!
Answers
Answer:
) The number of men who attended the sessions can be obtained by summing up the number of males in each session:
Total number of men = 12 + 18 + 17 = 47
Therefore, 47 men attended the sessions.
b) The number of people who attended Session 3 can be obtained by summing up the number of males and females in Session 3:
Total number of people in Session 3 = 17 (males) + 5 (females) = 22
Therefore, 22 people attended Session 3.
c) The sample size refers to the total number of attendees across all sessions. We can calculate it by summing up the number of males and females in each session:
Sample size = (12 + 8) + (18 + 9) + (17 + 5) = 69
Therefore, the sample size is 69.
d) To calculate the probability that a randomly selected person is male, we need to divide the number of males by the sample size:
Probability of selecting a male = Number of males / Sample size = 47 / 69 ≈ 0.6812
Therefore, the probability that a randomly selected person is male is approximately 0.6812 (rounded to four decimal places).
e) To calculate the probability that a randomly selected person attended Session 3, we need to divide the number of people who attended Session 3 by the sample size:
Probability of attending Session 3 = Number of people in Session 3 / Sample size = 22 / 69 ≈ 0.3188
Therefore, the probability that a randomly selected person attended Session 3 is approximately 0.3188 (rounded to four decimal places).
f) To calculate the probability that a randomly selected person is male and attended Session 3, we need to divide the number of males in Session 3 by the sample size:
Probability of being male and attending Session 3 = Number of males in Session 3 / Sample size = 17 / 69 ≈ 0.2464
Therefore, the probability that a randomly selected person is male and attended Session 3 is approximately 0.2464 (rounded to four decimal places).
On a map, 1 inch equals 20 miles. Of two cities are 3 inches apart on the map, how far are they actually apart?
Answers
Answer:
60 miles
Step-by-step explanation:
Since 1 inch on the map equals 20 miles, you just have to multiply 3 by 20.
3x20=60
1.Solve the LP model using the graphical method and Excel respectively. max==2x₂ + 3x₂ s.f. x₂ + 2x₂ ≤ 8 4x₁ 4x ≤ 12 X₁, X₂20

Answers
The solution of the LP model using the graphical method and MS Excel are;
Optimal solution is; x₁ = 4, and x₂ = 2, and the maximum value of the objective function is 14What is a LP model?The acronym LP stands for Linear Programming, which is a mathematical (modeling) method of optimizing a linear objective function based on a set constraints which are linear.
Graphical method:
The constraints on the graph are;
x₁ + 2·x₂ ≤ 8
4·x₁ ≤ 16
4·x₂ ≤ 12
The third constraint indicates; x₂ ≤ 3, which is the horizontal line, y = 3
The second constraint indicates; x₁ ≤ 4, which is the vertical line, x = 4
The first constraint indicates; x₂ ≤ 4 - (1/2)·x₁, which is a line with slope (-1/2), passing through the points (0, 4) and (8, 0)
The feasible region that satisfies all the constraints is shaded in the attached graph of the inequality, created with MS Excel
The maximising function indicates;
Point A (0, 0); z = 2 × 0 + 3 × 0 = 0
Point B (0, 3); z = 2 × 0 + 3 × 3 = 9
Point C (2, 3); z = 2 × 2 + 3 × 3 = 13
Point $ (4, 2); z = 2 × 4 + 3 × 2 = 14
Point E (4, 0); z = 2 × 4 + 3 × 0 = 8
The maximum value of z is 14, which is obtained at the point D(4, 2)
Excel Method;
The MS Excel Solver add-in can be used to solve the LP problem using the following steps;
Create a new spreadsheet in MS ExcelLabel column A1; Variables, B1: Coefficients, C1: Constraints 1, D1: Constraints 2, E1: Constraints 3, F1: RHSInput the variable names x₁ and x₂ in cells A₂ and A₃, respectivelyThe objective function coefficients 2 and 3 are entered into cells B2 and B3, respectivelyInput the constraint coefficients as follows; Input 1 in cell C2, 2 in cell D2, and 0 in cell E2 to represent the first constraint x₁ + 2·x₂ ≤ 8. Input 4 in cell C3, 0 in cell D3, and 0 in cell E3 to represent the second constraint 4·x₁ ≤ 16, and input 0 in cell C4, 4 in cell D4, and 0 in cell E4 to represent the third constraint, 4 × x₂ ≤ 12Input the right-hand side (RHS) coefficient in cells F2 to F4. Input 8 in cell F2, 16 in F3, and 12 in F4, to represent the RHS of the first second and third constraint respectivelySelect "Solver" in the "Data" tab at the top of the MS Excel window then click on "Solver" in the "Analysis" section. If the Solver is not visible, then it can be added using the "Add-ins" option in the "File" menu.Set the "Set Objective" field to cell B5 to compute the objective function in B5, set the "To" field to "Max", and set the "By Changing Variable Cells" field to cells A2:A3 (the location of the decision variables).Click the "Add" button in the "Constraints" section to add each of the three constraints. Set the "Cell Reference" field to the corresponding row in the "Constraints" section(C2:C4, D2:D4, and E2:E4, respectively), set the "Relation" field to "<=", and set the "Value" field to corresponding RHS value in column F (F2:F4).Close the "Add Constraint" window by clicking "OK", to return th the Solver Parameters window.Click "Solve" to solve the LP model. The solution once found, the solver will display the objective function value in cell B5, and the decision variable optimal values in cells A2:A3The optimal solution is obtained when x₁ = 4, x₂ = 2, and the maximum value of the objective function is 14, z = 2·x₁ + 3·x₂ = 14
Learn more in linear programming here: https://brainly.com/question/29750786
#SPJ1

Consider the following story:
Three men walk into a hotel and ask to share a room. The cost is going to be $270 for
the night. Each man puts in a $100 bill and they get 3 $10 bills in change. The bell boy
carries their luggage and they each decide to be generous and tip the bell boy their change.
The front desk realizes they miss-charged the men, so the bell boy takes a $20 bill change to
the room. The men realize that you can’t split the $20 bill evenly 3 ways so they add it onto
the tip. The bell boy is happy but then thinks to himself: ”If the room is $270 and they had
this extra $20 that’s only $290, where did the other $10 go?”
Explain what is wrong with the Bell Boy’s thoughts, and what is the correct math here.
Answers
Answer:
Step-by-step explanation:
The bell boy added $270 and $20 incorrectly. The $20 bill was something that was returned due to overcharching. On the other hand, $270 was the amount that they paid for their room. This only means that $20 should be deducted from $270 and that's the amount that they paid for their room while $30 and $20 are the amount that the bell boy received as a tip
Total money of the three men: 3($100) = $300
They paid $270 for the room: $300 - $270 = $30
Tip for the bell boy: $30 - $30 = $0
Amount overcharged to them: $0 + $20 = $20
Tip to the bell boy: $20 - $20 = $0
They were left with no more money from the original $300.
2. How can we solve for the degree of a polynomia which has more than one variable?
Answers
Answer:
To solve for the degree take the number that has the highest exponent. If they have equal exponents then see if you can simply further
Step-by-step explanation:
To solve for the degree take the number that has the highest exponent. If they have equal exponents then see if you can simply further