Find JOM (I WILL MARK BRAINLY)

It is true that the pond will be filled up after 13 hours of pumping at the same rate of sump pump.

A rate is a special ratio in which the two terms are in different units. For example, if a 12-ounce can of corn costs 69¢, the rate is 69¢ for 12 ounces. This is not a ratio of two like units, such as shirts. This is a ratio of two unlike units: cents and ounces.

Let the volume of the pond be x cubic unit

The rate of the pumping pipe is x/5 cubic unit/hour

The rate of the draining pipe = x/8cubic unit / hour.

after 13hours

The volume pumped into the pond =

x/5 × 8 = 13x/5 cubic unit

The volume of water drained =

x/8 × 13 = 13x/8 cubic unit.

Therefore the volume of water left =

13x /5 - 13x/8 = (104x - 65x)/40

= 39/40 of x

= 0.975 of x.

approximately to the nearest cubic units = 1 of x

Therefore it is true that the pond will be filled up after 13 minutes.

learn more about rate from

https://brainly.com/question/25793394

#SPJ1

Answer:

<D is congruent to <B

Step-by-step explanation:

They both have the 3 lines indicated on them

Answer:

Yes

Step-by-step explanation:

Answer:

1.58 *h=50.5 * 2.9

1.58 *h = 146.45

divide by 1.58

h=92.68987= 92.69

Step-by-step explanation:

The IRA (individual retirement account) of a 22-year-old college student, who deposits $55 into the account each month, will have a total balance at retirement. To calculate this, we need to consider the time period, the monthly deposit, and the annual percentage rate (APR).

The student plans on retiring at age 65, which means the IRA will have 65 - 22 = 43 years to grow. Since the student deposits $55 each month, we can calculate the total number of deposits over the 43-year period: 43 years * 12 months/year = 516 deposits.

To calculate the total balance at retirement, we need to consider the growth of the account due to the APR. The annual growth rate is 6%, which can be expressed as 0.06 in decimal form. To calculate the monthly growth rate, we divide the annual growth rate by 12: 0.06/12 = 0.005.

Using the formula for the future value of an ordinary annuity, we can calculate the total balance at retirement:
FV = PMT * [(1 + r)^n - 1] / r

Where:
FV = future value (total balance at retirement)
PMT = monthly deposit ($55)
r = monthly interest rate (0.005)
n = number of deposits (516)

Plugging in these values into the formula:
FV = 55 * [(1 + 0.005)^516 - 1] / 0.005

Calculating this equation, the IRA will contain $287,740.73 at retirement.

To know more about percentage , visit ;

https://brainly.in/question/10002322

#SPJ11

The total volume of Mountain Dew in this six-pack is approximately 212.058 cubic inches.

Assuming that each can in the six-pack of Mountain Dew is cylindrical in shape, we can use the formula for the volume of a cylinder to calculate the volume of each can, and then multiply that by the total number of cans in the pack.

The formula for the volume of a cylinder will be;

V = πr²h

where V is volume, r is radius (half the diameter), and h is height.

The radius of each can is 1.5 inches (half of 3 inches), and the height is 5 inches. So the volume of each can is;

V = π(1.5)²(5) = 35.343 cubic inches

To find the total volume of the six-pack, we need to multiply this by the number of cans;

Total volume = 35.343 cubic inches/can × 6 cans

= 212.058 cubic inches

Therefore, the total volume is  212.058 cubic inches.

To know more about cylinder here

https://brainly.com/question/16134180

#SPJ1

Answer:

いちまんいっせん

Step-by-step explanation:

Answer:

That is, 100 is just 百 hyaku, and 1000 is just 千 sen, but 10,000 is 一万 ichiman

and 11,000 is いちまんいっせん Ichiman Issen.

Answer:

x = 22, y = 12.

Step-by-step explanation:  

5x + 4 = 114                                  (opposite angles).

5x + 4 + 3x - 24 + 2y  = 180         (adjacent angles are supplementary)

From first equation:

5x = 110

x = 22.

Substituting for x in the second equation:

114 + 3(22) - 24 + 2y = 180

2y = 180 - 114 - 66 + 24

2y = 24

y = 12.

Answer:

33 sq units

Step-by-step explanation:

if you section it off into a rectangle and two triangles, the large rectangle that makes up most of the shape is 6x4 units or 24 sq units. each triangle is 3x3 units, so together they would make one 3x3 square. the 3x3 square would have an area of 9, and the answer is 24+9, or 33 sq units

(a) The limit of f(x) as x approaches 3 is  8/5

(b) The limit of f(x) as x approaches 3 is  8/7

To evaluate the limits in the given expressions, let's analyze them step by step:

(a) If lim(x→3) (x-3) = 5, find lim(x→3) f(x).

The given expression f(x) - 8/(x-3) suggests that f(x) is multiplied by 8/(x-3). Therefore, to find the limit of f(x), we can analyze the behavior of the expression 8/(x-3) as x approaches 3.

Since the denominator (x-3) approaches 0 as x approaches 3, we need to check the behavior of the numerator 8.

lim(x→3) (x-3) = 5 (given)

lim(x→3) 8/(x-3) = 8/5 (taking the reciprocal)

As x approaches 3, the expression 8/(x-3) approaches 8/5. Therefore, the limit of f(x) as x approaches 3 is:

lim(x→3) f(x) = lim(x→3) 8/(x-3) = 8/5

(b) If lim(x→3) (x-3) = 7, find lim(x→3) f(x).

Similarly, we analyze the given expression f(x) - 8/(x-3). Since f(x) is multiplied by 8/(x-3), we need to consider the behavior of 8/(x-3) as x approaches 3.

lim(x→3) (x-3) = 7 (given)

lim(x→3) 8/(x-3) = 8/7 (taking the reciprocal)

As x approaches 3, the expression 8/(x-3) approaches 8/7. Therefore, the limit of f(x) as x approaches 3 is:

lim(x→3) f(x) = lim(x→3) 8/(x-3) = 8/7

In summary:

(a) lim(x→3) f(x) = 8/5

(b) lim(x→3) f(x) = 8/7

Learn more about Denominator at

brainly.com/question/32621096

#SPJ4

The probability that he misses the train today is 0.135 or 13.5%.

P(Class runs late)=30%=0.30

P(Miss train ∣ Class runs late)=45%=0.45

General multiplication rule:

P(A and B)=P(A)×P(B ∣ A)

Using the general multiplication rule, we then obtain (and using that the student always catches his train if the class ends on time) :-

P( Miss train)=P( Miss train and Class runs late)=P(Class runs late)×P(Miss train ∣ Class runs late)

= 0.30×0.45

= 0.135

= or 13.5%.

So, the the probability that he misses the train today is 0.135 or 13.5%.

Learn more about Probability and multiplication rule here :-

https://brainly.com/question/11234923

#SPJ4

Answer:

x=0

Step-by-step explanation:

Subtract 1 from both sides

2x+1-1<1-1

Simplify the arithmetic

2x<1-1

Simplify the arithmetic

2x<0

Isolate the X

X=0

Answer:

0.976 or 97.6%

Step-by-step explanation:

To calculate the frequency of the recessive allele, we need to use the information provided about the frequency of the dominant trait.

Let's assume that the particular dominant trait is determined by a single gene with two alleles: the dominant allele (A) and the recessive allele (a).

Given that 45 out of 1,000 babies are born with the dominant trait, we can infer that the remaining babies (1,000 - 45 = 955) do not have the dominant trait and can be considered as the recessive trait carriers.

The frequency of the recessive allele (q) can be calculated using the Hardy-Weinberg equation:

q = sqrt((Recessive individuals) / (Total individuals))

In this case, the total number of individuals is 1,000, and the number of recessive individuals is 955.

q = sqrt(955 / 1,000)

Using a calculator, we can find the value:

q ≈ 0.976

Therefore, the frequency of the recessive allele is approximately 0.976 or 97.6%.

Answer:

\(X= 15\)

Step-by-step explanation:

Since the angles are equal the equation to solve would be:

\(3x + 20 = 5x - 50\)

you will subtract 3x from 5x and get 2x

\(20 = 2x -50\)

subtract 20 from 50 to get 30

\(2x= 30\)

divide each side by 2

\(\frac{2x}{2} = \frac{30}{2}\)

\(X= 15\)

Hope this helps

Answer:

Step-by-step explanation:

Adjust the parameters as needed, such as the step size (h) and the final x-value (xn), and run the code to obtain the solution for y(x).

The resulting plot will show the solution curve.

To solve the given set of differential equations using the Runge-Kutta method in MATLAB, we need to convert the second-order differential equations into a system of first-order differential equations.

Let's define new variables:

y = y(x)

z = dz/dx

Now, we have the following system of first-order differential equations:

dy/dx = z (1)

dz/dx = -k/(2y) (2)

To apply the Runge-Kutta method, we need to discretize the domain of x. Let's assume a step size h for the discretization. We'll start at x = 0 and proceed until x = infinite.

The general formula for the fourth-order Runge-Kutta method is as follows:

k₁ = h f(xn, yn, zn)

k₂ = h f(xn + h/2, yn + k₁/2, zn + l₁/2)

k₃ = h f(xn + h/2, yn + k₂/2, zn + l₂/2)

k₄ = h f(xn + h, yn + k₃, zn + l₃)

yn+1 = yn + (k₁ + 2k₂ + 2k₃ + k₄)/6

zn+1 = zn + (l₁ + 2l₂ + 2l₃ + l₄)/6

where f(x, y, z) represents the right-hand side of equations (1) and (2).

We can now write the MATLAB code to solve the differential equations using the Runge-Kutta method:

function [x, y, z] = rungeKuttaMethod()

   % Parameters

   k = 1;              % Constant k

   h = 0.01;           % Step size

   x0 = 0;             % Initial x

   xn = 10;            % Final x (adjust as needed)

   n = (xn - x0) / h;  % Number of steps

   % Initialize arrays

   x = zeros(1, n+1);

   y = zeros(1, n+1);

   z = zeros(1, n+1);

   % Initial conditions

   x(1) = x0;

   y(1) = 0;

   z(1) = 0;

   % Runge-Kutta method

   for i = 1:n

       k1 = h * f(x(i), y(i), z(i));

       l1 = h * g(x(i), y(i));

       k2 = h * f(x(i) + h/2, y(i) + k1/2, z(i) + l1/2);

       l2 = h * g(x(i) + h/2, y(i) + k1/2);

       k3 = h * f(x(i) + h/2, y(i) + k2/2, z(i) + l2/2);

       l3 = h * g(x(i) + h/2, y(i) + k2/2);

       k4 = h * f(x(i) + h, y(i) + k3, z(i) + l3);

       l4 = h * g(x(i) + h, y(i) + k3);

       y(i+1) = y(i) + (k1 + 2*k2 + 2*k3 + k4) / 6;

       z(i+1) = z(i) + (l1 + 2*l2 + 2*l3 + l4) / 6;

       x(i+1) = x(i) + h;

   end

   % Plotting

   plot(x, y);

   xlabel('x');

   ylabel('y');

   title('Solution y(x)');

end

function dydx = f(x, y, z)

   dydx = z;

end

function dzdx = g(x, y)

   dzdx = -k / (2*y);

end

% Call the function to solve the differential equations

[x, y, z] = rungeKuttaMethod();

Learn more about differential equations click;

https://brainly.com/question/32645495

#SPJ4

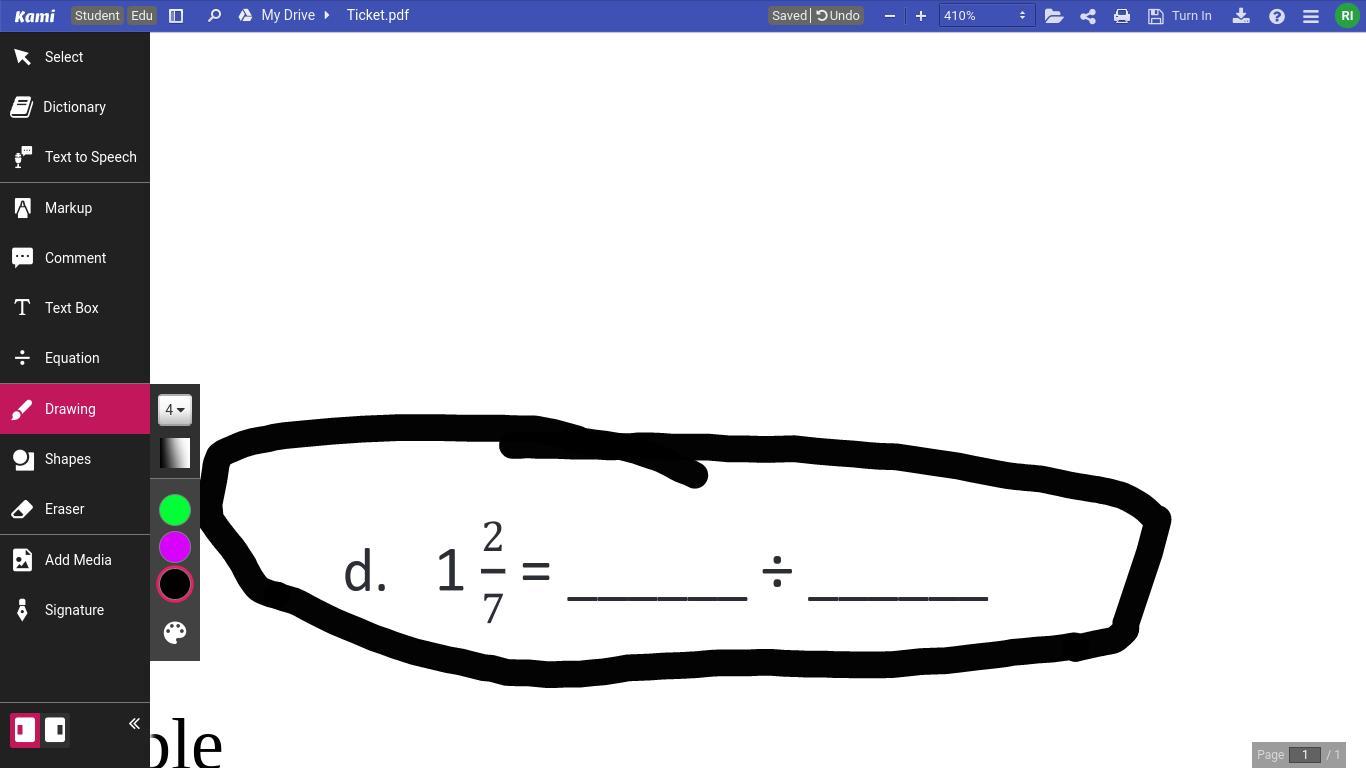
Answer:

Step-by-step explanation:

Volume of the pyramid:

Find base area:

Substitute value of the volume and find the height of the pyramid:

The boxes with h > 27 can fit the pyramid:

Area of base

Volume=1/3Area×Height

Height

So answers are

boxes of 28cm and 32cn

Answer:

No, -1 has two outputs

Step-by-step explanation:

Hope this helps!      :3

plz mark as brainliest!

Therefore, H(t) is increasing on the intervals (-∞, -1/\(\sqrt7\)) and (\(1/\sqrt7\), ∞) and decreasing on the interval (\(-1/\sqrt7\), \(1/\sqrt7\)).and There are no local or absolute maximum values for H(t).

To find the intervals on which the function H(t) is increasing or decreasing, we need to take the first derivative of H(t) and find its critical points.

a.) First derivative of H(t):

\(H'(t) = 12t^11 - 84/7t^13\)

\(= 12t^11(1 - 7t^2)/7t^2\)

The critical points are where H'(t) = 0 or H'(t) is undefined.

So, setting H'(t) = 0, we get:

\(12t^11(1 - 7t^2)/7t^2 = 0\)

\(t = 0\) or t = ±(\(1/\sqrt7\))

H'(t) is undefined at t = 0.

Now, we can use the first derivative test to determine the intervals on which H(t) is increasing or decreasing. We can do this by choosing test points between the critical points and checking whether the derivative is positive or negative at those points.

Test point: -1

\(H'(-1) = 12(-1)^11(1 - 7(-1)^2)/7(-1)^2 = -12/7 < 0\)

Test point: (-1/√7)

\(H'(-1/\sqrt7) = 12(-1/\sqrt7)^11(1 - 7(-1/\sqrt7)^2)/7(-1/\sqrt7)^2 = 12/7\sqrt7 > 0\)

Test point: (1/√7)

\(H'(1/\sqrt7) = 12(1/\sqrt7)^11(1 - 7(1/\sqrt7)^2)/7(1/\sqrt7)^2 = -12/7\sqrt7 < 0\)

Test point: 1

\(H'(1) = 12(1)^11(1 - 7(1)^2)/7(1)^2 = 5/7 > 0\)

Therefore, H(t) is increasing on the intervals (-∞, -1/√7) and (1/√7, ∞) and decreasing on the interval (-1/√7, 1/√7).

b.) To find the local and absolute extreme values of H(t), we need to check the critical points and the endpoints of the intervals.

Critical points:

\(H(-1/\sqrt7) \approx -0.3497\)

\(H(0) = 0\)

\(H(1/\sqrt7) \approx-0.3497\)

Endpoints:

H (-∞) = -∞

H (∞) = ∞

Since H (-∞) is negative and H (∞) is positive, there must be a global minimum at some point between -1/√7 and 1/√7. The function is symmetric about the y-axis, so the global minimum occurs at t = 0, which is also a local minimum. Therefore, the absolute minimum of H(t) is 0, which occurs at t = 0.

There are no local or absolute maximum values for H(t).

To know more about derivative visit:

https://brainly.com/question/23847661

#SPJ1

Answer:

5 5/9

Step-by-step explanation:

Answer:

I believe this is what they are asking on your problem.

The solution to the inequality graph is: (2/3, 16/3)

There are different types of inequalities such as:

Less than

Greater than

Less than or equal to

Greater than or equal to

Now, we are given the inequalities as:

y > 2x + 4

x + y ≤ 6

Now, the solution to both simultaneous inequalities will be the point at which both lines intersect each other and in this case the solution is:

(2/3, 16/3)

Read more about Inequality Graph at: https://brainly.com/question/11234618

#SPJ1

Complete question is:

This should be a smaller Scale. What is the solution to the graphed inequalities.

the answer is 87.75                  

Answer:

x = 34

Step-by-step explanation:

Just add 14 on both sides of the equal sign to get x = 34.

Hope this helps :)

Answer:

x = 34

Step-by-step explanation:

hope it helps a lot

that's the final answer

Answer:

2x+10=20 so x=5

Step-by-step explanation:

Answer:

y = 2x - 12

Step-by-step explanation:

(y-4)/(-4-4) = (x-8)/(4-8)

(y-4)/-8 = (x-8)/-4

y-4 = 2x - 16

y = 2x - 16 + 4

y = 2x - 12

Answer:

\(1\frac{3}{20}\)

Step-by-step explanation:

'23' fits into '20' one time. So, '1' would be the whole number. We would be left over with  '\(\frac{3}{20}\)'  as the remainder, so  '\(\frac{3}{20}\)' would be the fraction of the mixed number.  

Put them together, and you get: \(1\frac{3}{20}\)

The fraction is already in it's simplest form.

Brainilest Appreciated.

The solution for mixed fraction of number 23 / 20 is,

⇒ 23/20 = 1 3/20

We have to given that,

A number is,

⇒ 23 / 20

We can divide it for the mixed fraction as,

⇒ 23 / 20

20 ) 23 ( 1

    - 20

  --------------

          3

Therefore, It can be written as,

⇒ 23 / 20 = 1 3/20

Thus, The solution for mixed fraction of number 23 / 20 is,

⇒ 23/20 = 1 3/20

Learn more about the divide visit:

https://brainly.com/question/28119824

#SPJ6