Mathematics High School

Find g(1) if g(x) = x 2 + 1.

Answers

Answer 1

Answer:

g(x) = x^2 + 1

if x=1

g(1) = 1^2 + 1

g(1) = 1 + 1

g(1) = 2

Answer 2

Answer:

g(1) = 2

Step-by-step explanation:

I) Setup an equation to find g(1):

x^2 + 1

1^2 + 1

II) Solve:

1^2 + 1

= 1 + 1

= 2

Related Questions

Write the quadratic equation whose roots are 6 and 5, and whose leading coefficient is 1

Answers

Answer:

y = x³ - 12x² + 41x - 30

we continue the analysis of the olympic1500m.txt data set from problem set 8. but now we analyze the problem as one of constructing a confidence interval for a proportion.(a) Let X denote the number of races (out of 23 total races) won by a skater starting in the
outer lane. If there is no advantage of starting on the outer lane, then it is reasonable
to model X as having a Bin(23, p) distribution with p = 0.5. Explain why.
(b) Use the normal approximation to the binomial distribution to derive lower 95% and 98%
CIs for the unknown proportion p. (Hint: Week 9 Lectures, Part 2, Slides 16ff. You can
use Matlab, Wolfram Alpha, ... to solve the inequality.)
(c) Based on your 95% CI, are you 95% confident that skaters starting in the outer line are
indeed faster? What is your answer based on the 98% CI?
(d) Which of the CIs constructed in Question 2(c), Question 2(e), and Question 3(b) are
the least credible in the sense that some (or all) assumptions are (most likely) violated?

Answers

a. We can model X as having a Bin(23, p) distribution with p = 0.5 because if there is no advantage of starting on the outer lane

b. For a 95% confidence interval the lower bound of 0.432 and an upper bound of 0.831. For a 98% confidence interval the lower bound of 0.398 and an upper bound of 0.865.

c. Based on the 95% and 98% CI, we can say that we are confident that the races won by skaters starting in the outer lane.

d. The CI constructed in Question 2(e) is the least credible

(a) Since there is no benefit to beginning on the outer lane, we can model X as having a Bin(23, p) distribution with p = 0.5., then the probability of winning a race starting in the outer lane is the same as the probability of losing, which is 0.5.

We can think of each race as a Bernoulli trial, where success is defined as winning the race starting in the outer lane, and failure is defined as losing the race starting in the outer lane. Since the outcome of each race is independent and the probability of success is constant for each trial, X follows a binomial distribution.

(b) Using the normal approximation to the binomial distribution, we have:

The sample proportion of races won by skaters starting in the outer lane is p' = X/n = 12/23.

The standard error of p' is SE(p') = sqrt((p'(1-p'))/n) = sqrt((12/23)*(11/23)/23) ≈ 0.145.

For a 95% confidence interval, we can use the formula: p' ± 1.96 SE(p'). This gives a lower bound of 0.432 and an upper bound of 0.831.

For a 98% confidence interval, we can use the formula: p' ± 2.33 SE(p'). This gives a lower bound of 0.398 and an upper bound of 0.865.

(c) Based on the 95% CI, we can say that we are 95% confident that the true proportion of races won by skaters starting in the outer lane is between 0.432 and 0.831. Since the interval does not include the value 0.5, we can conclude that skaters starting in the outer lane are indeed faster with a 95% level of confidence.

Based on the 98% CI, we can say that we are 98% confident that the true proportion of races won by skaters starting in the outer lane is between 0.398 and 0.865. Since the interval does not include the value 0.5, we can conclude that skaters starting in the outer lane are indeed faster with a 98% level of confidence.

(d) The CI constructed in Question 2(e) is the least credible because it assumes that the sample proportion p' is close to the true proportion p, which may not be the case if the sample size is small or the true proportion is close to 0 or 1.

The CIs constructed in Question 2(c) and Question 3(b) use the normal approximation to the binomial distribution, which is valid for large sample sizes and when the success-failure condition is satisfied.

Learn more about confidence interval at https://brainly.com/question/29734515

#SPJ11

Given the demand function,
Q=54−5P+4PA+0.1Y,
where Q is the quantity of chocolate demanded, P is the price of chocolate, PA is the price of an apple and Y is income, find:
(i) the own price elasticity of demand for chocolate
(ii) the cross price elasticity of demand (
iii) the income elasticity of demand where P=3,PA =2 and Y=100. Comment on the economic significance of your answers.

Answers

The income elasticity of demand is positive, implying that chocolate is a normal good = 0.037

The demand function, Q = 54−5P + 4PA + 0.1Y.

Where Q is the quantity of chocolate demanded, P is the price of chocolate, PA is the price of an apple, and Y is income.

(i) The own-price elasticity of demand for chocolate, we first need to find the expression for it.

The own-price elasticity of demand can be expressed as:

Own-price elasticity of demand = (Percentage change in quantity demanded) / (Percentage change in price)Or,E

P = (ΔQ / Q) / (ΔP / P)E P = dQ / dP * P / Q

Let's calculate the own-price elasticity of demand:

EP= dQ / dP * P / Q= (-5) / (54 - 5P + 4PA + 0.1Y) * 3 / 30

= -0.1667

So, the own-price elasticity of demand for chocolate is -0.1667.

(ii) The cross-price elasticity of demand, we must first determine the expression for it.

The cross-price elasticity of demand can be expressed as:

Cross-price elasticity of demand

= (Percentage change in quantity demanded of chocolate) / (Percentage change in price of apples) Or, E

PA = (ΔQ / Q) / (ΔPA / PA)E PA = dQ / dPA * PA / Q

Let's calculate the cross-price elasticity of demand:

EP = dQ / dPA * PA / Q= (4) / (54 - 5P + 4PA + 0.1Y) * 2 / 30= 0.0296

So, the cross-price elasticity of demand is 0.0296.

(iii) The income elasticity of demand can be expressed as:

Income elasticity of demand = (Percentage change in quantity demanded) / (Percentage change in income)Or,E

Y = (ΔQ / Q) / (ΔY / Y)E Y = dQ / dY * Y / Q

Let's calculate the income elasticity of demand: EY = dQ / dY * Y / Q= (0.1) / (54 - 5P + 4PA + 0.1Y) * 100 / 30

= 0.037

The own-price elasticity of demand is negative, meaning that the quantity demanded of chocolate decreases when the price of chocolate increases.

The cross-price elasticity of demand is positive, indicating that chocolate and apples are substitute goods.

For more related questions on income elasticity:

https://brainly.com/question/29564308

#SPJ8

Find the length of the missing side. Write your answer as a number rounded to 2 decimal
places. Example: 2√3 = 3.46
If m/C=
= 30° and AB =18, find the length of BC =
A
C
B

Answers

Answer: BC = 80

Step-by-step explanation:

One of the many Pythagoean Triplets is 18, 80, and 82. This is the only one with 18 as one of the sides other than the hypotnyse.

find x in this two examples

Answers

The values of x in both figures are 45 and 34, respectively.

The value of x in (a)

Start by calculating the angle CAB using:

CAB + ABC + BCA = 180 --- angles in a triangle

The triangle is an isosceles triangle.

So, we have:

CAB + ABC + CAB = 180

Evaluate

2CAB + 25 + 75 = 180

This gives

CAB = 40

Calculate angle BEA using:

BEA + CAB + ABE = 180 --- angles in a triangle

This gives

BEA + 40 + 25 = 180

Evaluate

BEA = 115

Vertical angles are equal.

So, we have:

CED = BEA = 115

Calculate angle EDC using:

EDC + CED + DCE = 180 --- angles in a triangle

This gives

EDC + 115 + 30 = 180

Evaluate

EDC = 35

Opposite angles of quadrilaterals add up to 180.

So, we have:

x + EDC + ABC = 180

This gives

x + 35 + 25 + 75 = 180

Evaluate

x = 45

Hence, the value of x is 45

The value of x in (b)

Start by calculating the angle DEC using:

DEC + CDE + EED = 180 --- angles in a triangle

This gives

DEC + 18 + 30 = 180

Evaluate

DEC = 132

Vertical angles are equal.

So, we have:

AEB = DEC = 112

Calculate angle EAB using:

EAB + AEB + ABE = 180 --- angles in a triangle

This gives

EAB + 112 + 42 = 180

Evaluate

EAB = 26

Triangle ABC is an isosceles triangle.

So, we have:

BCE = EAB = 26

Calculate angle CBE using:

CBE + BCE + CEB = 180 --- angles in a triangle

Where CEB = 180 - DEC --- angle on a straight line

So, we have:

CBE + BCE + 180 - DEC = 180

This gives

CBE + 26 + 180 - 112 = 180

Evaluate

CBE = 86

Opposite angles of quadrilaterals add up to 180.

So, we have:

x + EDC + ABC = 180

This gives

x + 18 + 42 + 86 = 180

Evaluate

x = 34

Hence, the value of x is 34

Note that the figures are labeled to ease explanation (see attachment)

Answers

Answer:

$146.1

Step-by-step explanation:

Anya has $25,000 which she recently received from a trust fund, which she intends to invest in an account earning 12% annually. a) How many years would it take Anya to accumulate $40,000. b) If Anya's goal is to save $40,000 in just 3 years, what rate of return must she earn annually on her account. Show all workings and formulae

Answers

a) It would take Anya approximately 4 years to accumulate $40,000 with an annual interest rate of 12%. b) Anya must earn an annual rate of return of approximately 12.6% to save $40,000 in 3 years.

a) To calculate the number of years it would take Anya to accumulate $40,000, we can use the future value formula for compound interest:

Future Value = Present Value * (1 + interest rate)ⁿ

Where:

Future Value = $40,000

Present Value = $25,000

Interest rate = 12% = 0.12

n = number of years

Substituting the given values into the formula, we have:

$40,000 = $25,000 * (1 + 0.12)ⁿ

Dividing both sides of the equation by $25,000, we get:

(1 + 0.12)ⁿ = 40,000 / 25,000

(1.12)ⁿ = 1.6

To solve for n, we can take the logarithm of both sides of the equation:

n * log(1.12) = log(1.6)

Using a calculator, we find that log(1.12) ≈ 0.0492 and log(1.6) ≈ 0.2041. Therefore:

n * 0.0492 = 0.2041

n = 0.2041 / 0.0492 ≈ 4.15

b) To calculate the required rate of return for Anya to save $40,000 in just 3 years, we can rearrange the future value formula:

Future Value = Present Value * (1 + interest rate)ⁿ

$40,000 = $25,000 * (1 + interest rate)³

Dividing both sides of the equation by $25,000, we have:

(1 + interest rate)³ = 40,000 / 25,000

(1 + interest rate)³ = 1.6

Taking the cube root of both sides of the equation:

1 + interest rate = ∛1.6

Subtracting 1 from both sides, we get:

interest rate = ∛1.6 - 1

Using a calculator, we find that ∛1.6 ≈ 1.126. Therefore:

interest rate = 1.126 - 1 ≈ 0.126

To express the interest rate as a percentage, we multiply by 100:

interest rate = 0.126 * 100 = 12.6%

To know more about annual interest rate,

https://brainly.com/question/33696451

#SPJ11

consider the function l(x,y)shown in the contour diagram at the right.l(x,y)is the percentage a student earns on an exam as a function of x,the number of hours the student slept the night before,and y.how full their stomach is before the exam on a scale of 1 to 10.

Answers

Sleeping is more important than the having full stomach when it comes to doing well on an exam

Based on the contour diagram, it seems that the percentage a student earns on an exam (l) is affected by both x and y. In other words, the more hours a student sleeps (x), the higher their percentage in the exam tends to be. Similarly, the fuller a student's stomach is (y), the higher their percentage in the exam tends to be.
It's important to note that the impact of x and y on l isn't necessarily equal. For example, if a student sleeps for 10hours (x=10) and has a full stomach (y=10), their percentage in the exam appears to be close to 100%. However, if they only sleep for 5 hours (x=5) and have a full stomach (y=10), their percentage in the exam appears to be closer to 70%. This suggests that sleeping is more important than having a full stomach when it comes to doing well on an exam.
Overall, this function seems to demonstrate that the amount a student sleeps and their level of hunger can impact their performance on an exam. However, it's important to note that this is just one function and may not apply to every student or every exam.

Learn more about contour diagram here:

https://brainly.com/question/30077087

#SPJ11

Quiz: Relations and Functions

HS: Integrated Math 2B [M] (Sequential) (GP)/ Part 3: Inequalities and Systems / 01:Inequalities ar

2. Which relation defined by a set of ordered pairs is not a function?

O

{(1, -1), (2,-2), (0, 0), (1, 1), (2, 2)}

{(1, -1), (4-2), (9,-3), (16,-4), (25,-5)}

{(1, 1), (2, 4), (3, 9), (4,16), (5,25))

{(-1,1).(-2,4),(-3, 9), (-4,16), (-5, 25)}

Answers

According to question the answer is: {(1, -1), (2,-2), (0, 0), (1, 1), (2, 2)}

The relation defined by a set of ordered pairs is not a function if there exists at least one x-value with two or more corresponding y-values.

In the given options, the relation O {(1, -1), (2,-2), (0, 0), (1, 1), (2, 2)} is not a function because x-value 1 has two corresponding y-values -1 and 1.

what is relation ?

In mathematics, a relation is a set of ordered pairs that expresses a connection between two objects. The objects in question can be numbers, sets, or any other mathematical entities. The pairs are written in the form (a, b), where a is the first element of the pair and b is the second element. For example, {(1,2), (2,4), (3,6)} is a relation that expresses the connection between the numbers 1, 2, and 3 and their corresponding multiples of 2. A relation can be represented as a graph, a table, or a formula.

To learn more about ordered pairs visit:

brainly.com/question/30805001

#SPJ11

please find the answer to this question

Answers

down 3 units i rhink it is

A national standard requires that public bridges over 20 foot in length must be inspected and rated overy 2 yours. The rating scalo ranges from 0 (poorest rating) to 9 (highost rating). A group of engineers used aprobabilistio model to forecast the inspection ratings of all major bridges in a city. For the year 2020, the enginoors forecast that 8% of all major bridges in that city will have ratings of 4 or below. Comploto parts aand bea. Use tho forecast to find the probability that in a random sample of 8 major bridgos in the city, at least 3 will have an inspection rating of 4 or below in 2020,PIX23) - (Round to five decimal places as needed.)

Answers

We can solve the problem by using the probability binomial distribution model. The formula is:

$P(X=x)=(^n_x)p^xq^{n-x}$

Recall that:

$(^n_x)=^nC_x$

Given:

number of samples(n) = 8

x = 3

8% of all major bridges in that city will have ratings of 4 or below implying that the probability of a bridge having a rating of 4 or below is 0.08.

Hence,

$\begin{gathered} p\text{ = 0.08} \\ q\text{ = 1-p } \\ q\text{ = 1-0.08} \\ q\text{ = 0.92} \end{gathered}$

The probability that in a random sample of 8 major bridges in the city, at least 3 will have an inspection rating of 4 or below in 2020 would be:

$\text{Probability of at least 3 = 1 - Probability of at most }2$

Probability of at most 2 can be reduced to:

$P(x\text{ }<\text{ 3) = P(x =2) + P(x = 1) + P(x = 0)}$

Evaluating the expression, we have:

$\begin{gathered} P(x\text{ }<3)=^8C_2(0.08)^2(0.92)^{8-2}+^8C_1(0.08)^1(0.92)^{8-1}+^8C_0(0.08)^0(0.92)^{8-0} \\ =\text{ 0.10866 + 0.35702 + }0.51322 \\ =\text{ 0.9789}0 \end{gathered}$

The probability that at least 3 will have a rating of 4 and below:

$\begin{gathered} P(x\text{ }\ge3)\text{ = 1 - P(x }<\text{ 3)} \\ =\text{ 1 - 0.97890} \\ =\text{ 0.02110} \end{gathered}$

Answer:

0.02110

The susceptibility of the root stocks of a variety of orange tree to a specific larva is investigated by a group of researchers. Forty orange trees are exposed to the larva and then examined by the researchers 6 months after exposure. The number of larvae per gram is recorded on each root stock. The mean and standard deviation of the logarithm of the counts are recorded to be 9.02 and 1.12, respectively.

Required:

Use the sample information to construct a 90% confidence interval on the mean of the logarithm of the larvae counts.

Answers

The confidence interval on the mean of the logarithm of the larvae counts is (8.7, 9.33) for a 90% confidence level.

Given that, the number of larvae per gram is recorded on each root stock and the mean and standard deviation of the logarithm of the counts are recorded to be 9.02 and 1.12 respectively. We have to construct a 90% confidence interval on the mean of the logarithm of the larvae counts.

Confidence level = 90%

α = 1 - 0.90 = 0.10

The sample size, n = 40

We know that for the normal distribution, the formula for the confidence interval is given as:

CI = x ± z (σ/√n)

Where, x = sample mean, z = z critical value, σ = population standard deviation, n = sample size

Here, the standard deviation of the population is not known so, we use the standard error which is given by the formula

σ / √n = s

Where s = sample standard deviation.

The confidence interval for the mean is given as:

CI = x ± t* (s/√n)

At a 90% confidence level, the value of t0.05, 39 = 1.684

We have to calculate the mean and standard deviation of the logarithm of the counts. They are: Mean, x = 9.02, Standard deviation, s = 1.12√n = √40 = 6.32s/√n = 1.12/6.32 = 0.1776

So, the confidence interval is given as:

CI = 9.02 ± 1.684 × 0.1776 = (8.7, 9.33)

Learn more about Confidence interval:

https://brainly.com/question/17097944

#SPJ11

Scientific notation please help me!!

Answers

Step-by-step explanation:

See image

Which step is necessary for incorporate randomization into a simulation? (1 point) OUse a chance device. O Create a data table. Run the simulation more than once. Write an alternative hypothesis.

Answers

The step necessary for incorporating randomization into a simulation is to use a chance device.

A chance device, such as a random number generator, is necessary to introduce randomness into the simulation. This allows the simulation to generate random outcomes that reflect the uncertainty and variability of real-world situations. By incorporating randomization, the simulation can simulate a range of possible outcomes and estimate the probabilities of different outcomes occurring.

Creating a data table and running the simulation more than once are important steps in a simulation, but they are not specifically related to incorporating randomization. Writing an alternative hypothesis is also not related to incorporating randomization into a simulation, but rather a step in the hypothesis testing process.

To know more about randomization,

https://brainly.com/question/30841295

#SPJ11

A culture of bacteria obeys the law of uninhabited growth. If 500 bacteria are present initially and there are 800 after 1 hour, how many will be present in the culture after 5 hours

Answers

The estimated number of bacteria present in the culture after 5 hours as per exponential growth is equal to 5,240.

Initial population size (N₀) = 500 bacteria

Population size after 1 hour (N) = 800 bacteria

let us consider,

N₀ is the initial population size,

N is the population size at a given time,

k is the growth rate constant,

t is the time in hours,

e is the base of the natural logarithm (approximately 2.71828).

To determine the number of bacteria present in the culture after 5 hours,

Use the exponential growth formula for uninhibited growth,

N = N₀ × $e^{(kt)$

To find the growth rate constant (k), rearrange the formula as follows,

⇒k = ln(N / N₀) / t

⇒k = ln(800 / 500) / 1

⇒k = ln(1.6)

Using a calculator, we find that k ≈ 0.470

Now, use the growth formula to calculate the population size after 5 hours,

N = N₀ × $e^{(kt)$

N = 500 ×$e^{(0.470 \times 5)$

N = 500 × $e^{2.35$

Using a calculator, we find that $e^{2.35$ ≈ 10.48

⇒N ≈ 500 × 10.48

⇒N ≈ 5240

Therefore, it is estimated that there will be approximately 5,240 bacteria present in the culture after 5 hours using exponential growth .

learn more about exponential growth here

brainly.com/question/12490064

#SPJ4

x + 5 - 12
How can I do this

Answers

Answer: x − 7~Well, to find the answer you need to remove the variable 'x' because we don't know the value of 'x' then subtract 5 from 12.12 - 5 = 7~Then you add the variable back to the simplified equation and since you SUBTRACTED 5 from 12, you will also subtract 'x' from 7.x - 7~And there is your simplified answer. 8 - 7~

Hope you have a good day, Loves!

Also if I'm right can you let me know, please?

Also Also if I am right can I please have Brainliest??

You don't need to, I'm just glad I could help. ^^

answer is x-7

your welcome.

Pleas help me and explain

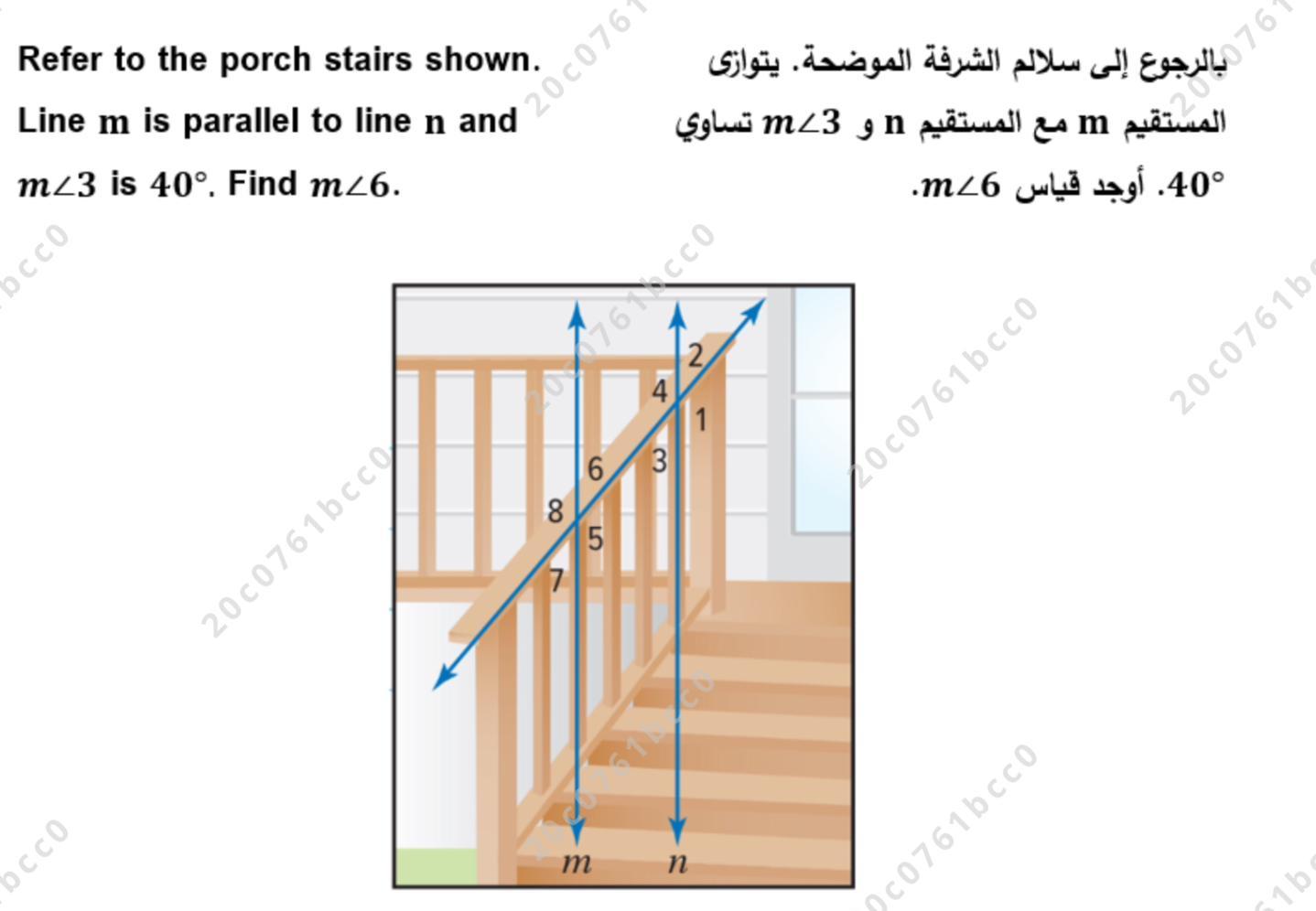
Answers

Answer:

m6=40

Step-by-step explanation:

m3=40

m6=40(alternate angle)

I need help I don't understand this.

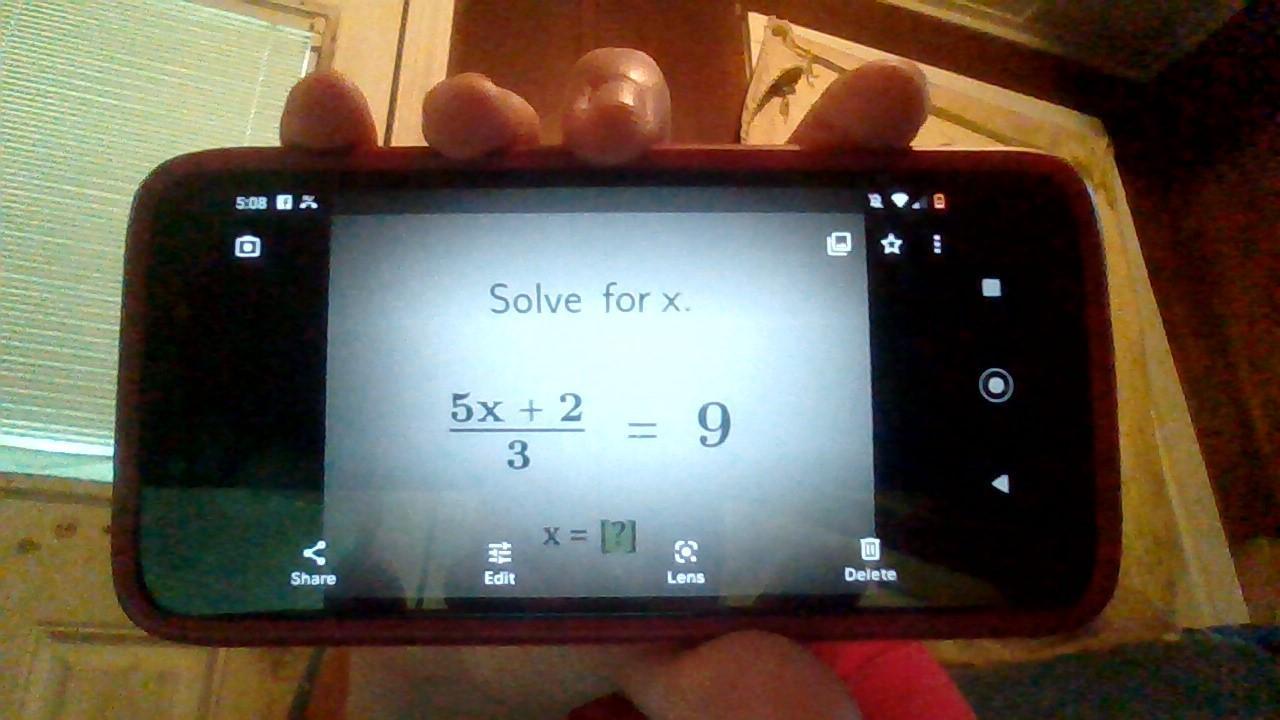
Answers

Answer:

x=5

Step-by-step explanation:

(5x+2)/3 = 9

Multiply each side by 3

(5x+2)/3 *3 = 9*3

5x+2 = 27

Subtract 2 from each side

5x+2-2 = 27-2

5x = 25

Divide by 5

5x/5 = 25/5

x =

Find an LU factorization of the matrix A (with L unit lower triangular). A=
⎣
⎡

4
−8
10
−8
8

−4
3
5
−7
7

6
−7
0
3
−3

⎦
⎤

Answers

The LU factorization of matrix A is A = LU, where L = [[1, 0, 0], [-2, 1, 0], [1.5, -3, 1]] and U = [[4, -8, 10], [0, 24, -27], [0, 0, -12.5]].

Let's go step by step to find the LU factorization of matrix A.

Matrix A:

A =

[4, -8, 10]

[-8, 8, -7]

[6, -7, 3]

Step 1:

Initialize the L matrix as an identity matrix of the same size as A.

L =

[1, 0, 0]

[0, 1, 0]

[0, 0, 1]

Step 2:

Perform Gaussian elimination to obtain U.

- Multiply the first row of A by (1/4) and replace the first row of A with the result.

A =

[1, -2, 2.5]

[-8, 8, -7]

[6, -7, 3]

- Subtract 8 times the first row of A from the second row of A and replace the second row of A with the result.

A =

[1, -2, 2.5]

[0, 24, -27]

[6, -7, 3]

- Subtract 6 times the first row of A from the third row of A and replace the third row of A with the result.

A =

[1, -2, 2.5]

[0, 24, -27]

[0, 5, -12.5]

Step 3:

Update the L matrix based on the operations performed during Gaussian elimination.

L =

[1, 0, 0]

[0, 1, 0]

[0, 0, 1]

Step 4:

The resulting matrix A is the upper triangular matrix U.

U =

[1, -2, 2.5]

[0, 24, -27]

[0, 5, -12.5]

Therefore, the LU factorization of matrix A is:

L =

[1, 0, 0]

[0, 1, 0]

[0, 0, 1]

U =

[1, -2, 2.5]

[0, 24, -27]

[0, 5, -12.5]

learn more about LU factorization of matrix from this link.

https://brainly.com/question/33069156

#SPJ11

There are a total of 64 students in the anime club and student council. Student council has 10 more students than anime club how many are in each

Answers

Answer:

27 in the anime club and 37 in student council

Step-by-step explanation:

there are 64 students

if you divide 64/2 there are 32 in both

32+32=64

then if you give 5 from one to the other

27+37=64

Answer:

student councel has 37 anime club has 27

Step-by-step explanation:

What is the product of (4i) and (4+i)

Answers

Answer:

-4 + 16 i

Step-by-step explanation:

You are dealing with imaginary numbers so i dont remember y but i know that it is that answer

Answer:

- 4 + 16i.

Step-by-step explanation:

4i(4 + i)

= 16i + 4i^2 Now i^2 = -1 so we have:

16i - 4 (answer)

The turtle travels 19 inches in one hour. At that rate, how far can the turtle go in 39 hours?

Answers

Answer:

19 inches is 48.26 and 39 hours is 2340 so 2340/48.26=48.427

Step-by-step explanation:

please help me, ill give u a brainiest

Answers

$ distance = | \frac{(- 4 \times 1) + (- 1 \times 1)-7}{ \sqrt{ {( - 4)}^{2} + {( - 1)}^{2} } } | \\= \frac{ - 12}{ \sqrt{17 } } \\ = \frac{ - 12 \sqrt{17} }{17} \\ = - 2.91$

4. Do the following side lengths form a triangle?

52, 37, 42

Answers

Answer:

Step-by-step explanation:

52+37+42 should be 180 but its not so it does not form a triangle

I hope you under stand

Answer:

yes

Step-by-step explanation:

use the triangle inequality theorem, where sides are 'a', 'b', and 'c':

all three of these must be true in order to have a triangle:

a+b > c

a+c > b

b+c > a

is 37 + 42 > 52 Yes

is 37 + 52 > 42 Yes

is 52 + 42 > 37 Yes

Test if the slope significant for the next values. β1=0.0943 , seβ1=0.107 and alpha 0.05.
6. Write the null and alternative hypothesis. (2 points
7. Calculate t-test statistic 8. Write tc, degrees of freedom and decision rule. 9. Conclusion.

Answers

The null and alternative hypotheses are:

H0: β1 = 0 (The slope is not significant.)

H1: β1 ≠ 0 (The slope is significant.)

Here,β1=0.0943seβ1=0.107α=0.05

Test the slope significance and find the t-test statistic.

We need to find the t-test statistic so that we can compare it with the t-distribution, whose distributional properties we know, to determine if we can reject or fail to reject the null hypothesis.t-test statistic is calculated by dividing the value of β1 by its standard error (seβ1) and taking the absolute value of this quotient.

t-test statistic = | β1/seβ1 | = |0.0943/0.107| = 0.881

The degrees of freedom (df) associated with this t-test are df = n - 2, where n is the sample size for the explanatory variable x.

In this problem, the decision rule and conclusion are as follows:

Decision Rule: Reject the null hypothesis if |t-test statistic| > tc where tc is the critical value obtained from the t-distribution with df degrees of freedom and a significance level of α/2 in each tail.

Conclusion: The slope is not significant if we fail to reject the null hypothesis, but the slope is significant if we reject the null hypothesis. Since the t-test statistic (0.881) is less than the critical value (1.987), we fail to reject the null hypothesis. Therefore, we conclude that the slope is not significant.

To know more about null and alternative hypotheses:

https://brainly.com/question/33444525

#SPJ11

The distance h a body will move in a free fall is expressed by the formula h=1/2 gt2 if g =980 cm per sec2 and t= 20 sec, the distance h is

Answers

Solution

Given the distance h as

$h=\frac{1}{2}t^2$

Here,

$\begin{gathered} g=980\text{ cm/sec}^2 \\ \\ t=20\text{ sec} \end{gathered}$

Therefore, the distance h is: 196000 cm

$h=\frac{1}{2}\times980\times20^2=196000\text{ cm}$

Olivia flips a two-sided counter and then spins a spinner with six equal-size sections labeled 1 through 6. One side of the counter is red. The other side is yellow. She performs this experiment 80 times. The relative frequency of tossing red and spinning a number greater than three was 2/5 . What is the difference between the number of expected outcomes and the number of actual outcomes?

Answers

Answer:

Step-by-step explanation:

A 2 - sided counter ; (red, yellow)

A spinner (1,2,3,4,5,6)

Number of trials = 80

P(red and number > 3) :

P(red) = 1/2 ;

P(number >3) : numbers greater Than 3 = (4, 5, 6)

Hence, P(number <3) = 3 /6 = 1/2

Theoretical probability = 1/2 *1/2 = 1/4

Expected number of outcomes :

1/4 * number of trials

1/4 * 80 = 20

Experimental outcome :

Relative frequency = number of outcomes / number of trials

Relative frequency = 2/5

Hence,

2/5 = number of outcomes / 80

Cross multiply :

160 = number of outcomes * 5

Number of outcomes = 160 /5 = 32

Actual outcomes = 32

Difference between actual and expected :

32 - 20 = 12

How to write standard deviation and mean in stats cordinate.

Answers

In statistics, the standard deviation (SD, also represented by the Greek letter sigma σ or the Latin letter s) is a measure that is used to quantify the amount of variation or dispersion of a set of data values.

How do I do number 2 ? Someone please helpp w

Answers

Answer:

yes it is a function

Step-by-step explanation:

You have to take the numbers and see if any of them are the same in the X column if their are some of the same numbers you only write the number once. than you connect the numbers to the given output. If any numbers have 2 outputs it is not a function.