Answers
Answer:
Domain is all real numbers.
Range is all real numbers > 3.
Minimum y-value is 3 (when x = 2).
No maximum.
Related Questions
please help me otherwise I will fail (1/2 + 1/2)* 700
Answers
Answer: 700
Step-by-step explanation:
Answer:
700
Step-by-step explanation:
copy and paste
A syllabus has the following weighted grade scale: 15% HW 60% Exams 25% Final The lowest exam from the class will be dropped. A student had the following scores: 100% HW 90% Exam 1, 86% Exam 2, 92% Exam 3, 84% Exam 4 78% Final. Calculate the final grade in the course.
Answers
To calculate the final grade in the course, we need to take into account the weighted grade scale and the fact that the lowest exam score will be dropped.
Let's break down the calculation step by step:
Calculate the average exam score after dropping the lowest score:
Exam 1: 90%
Exam 2: 86%
Exam 3: 92%
Exam 4: 84%
We drop the lowest score, which is Exam 2 (86%), and calculate the average of the remaining three exam scores:
Average exam score = (90% + 92% + 84%) / 3
= 88.67%
Calculate the weighted score for each category:
Homework (HW): 15% of the final grade
Exams (average of three exams): 60% of the final grade
Final Exam: 25% of the final grade
Weighted HW score = 100% * 15%
= 15%
Weighted Exam score = 88.67% * 60%
= 53.20%
Weighted Final Exam score = 78% * 25%
= 19.50%
Calculate the final grade:
Final Grade = Weighted HW score + Weighted Exam score + Weighted Final Exam score
Final Grade = 15% + 53.20% + 19.50%
= 87.70%
The final grade in the course, taking into account the weighted grade scale and dropping the lowest exam score, is 87.70%
To know more about weighted grade, visit
https://brainly.com/question/17714990
#SPJ11
X-3<9
What’s the answer to this everbody should know

Answers
Answer:
x<12
Step-by-step explanation:
Let's solve your inequality step-by-step.
x−3<9
Step 1: Add 3 to both sides.
x−3+3<9+3
x<12
Answer:
x<12
HELP ME!!! I WILL GIVE BRAINLIEST IF YOU WANT!!

Answers
Answer:
the one with the answer -10
Step-by-step explanation:
Answer:
So you do -8 + -2 which equals -10. it is the 3rd answer
Step-by-step explanation:
HELPPP !my teacher gave us 2 minutes?

Answers
Answer: the fraction form is 331/500
Step-by-step explanation:
Cassius Corporation has provided the following contribution format income statement.Assume that the following information is within the relevant range.Sales (7,000 units)$210,000Variable expenses136,500Contribution margin73,500Fixed expenses67,200Net operating income$6,300The number of units that must be sold to achieve a target profit of $31,500 is closest to:A) 42,000 unitsB) 16,400 unitsC) 35,000 unitsD) 9,400 units
Answers
Cassius Corporation needs to sell to make a profit of $31,500 to sell the number of units that needs to be sold is 9,400 units. It can be found this out by using a formula that takes into account the company's sales revenue, variable expenses, fixed expenses, and contribution margin.Therefore Option D is correct.
The contribution margin is the amount of money left over from sales revenue after deducting variable expenses. In this case, we know that Cassius Corporation's contribution margin is $73,500.
To find out how many units the company needs to sell, we can use the following formula:
(Number of units * Contribution margin per unit) - Fixed expenses = Target profit
We know that the fixed expenses are $67,200 and the target profit is $31,500.
The contribution margin per unit by dividing the contribution margin by the number of units sold, which in this case is 7,000 units. This gives us a contribution margin per unit of $10.50.
Substituting these values into the formula, we get:
(Number of units * $10.50) - $67,200 = $31,500
Simplifying this expression:
(Number of units * $10.50) = $98,700
Number of units = $98,700 / $10.50
Number of units = 9,400 (rounded to the nearest whole unit)
The number of units that must be sold to achieve a target profit of $31,500 is closest to 9,400 units. Option (D) is correct.
To practice more questions about 'target profit':
https://brainly.com/question/14636659
#SPJ11
Please help me I am really confused and need help with this.

Answers
Answer:
Step-by-step explanation:
y=10
2) Natalie's school is selling tickets to a choral performance. On the first day of ticket sales the
school sold 7 senior citizen tickets and 6 child tickets for a total of $156. The school took in
$120 on the second day by selling 7 senior citizen tickets and 3 child tickets. Find the price of a
senior citizen ticket and the price of a child ticket.
Answers
Answer:
both cost $12
Step-by-step explanation:
Let's say the price of a senior citizen ticket is s dollars and the price of a child ticket is c dollars.
For, say, 7 senior citizen tickets, the cost would be s 7 times, or s * 7. Similarly, 6 child tickets would cost 6c. The total amount of (senior citizen ticket cost) + (child ticket cost) would equal the total sales.
Therefore,
first day:
7s + 6c = 156
second day:
7s + 3c = 120
7s + 6c = 156
7s + 3c = 120
we can solve this by solving for c in terms of s in one equation and plugging that into the other equation
7s + 6c = 156
subtract 7s from both sides to isolate the c and its coefficient
156 - 7s = 6c
divide both sides by 6 to isolate c
(156-7s)/6 = c
26-(7/6)s = c
plug that into the other equation
7s+3c = 120
7s + 3 (26-(7/6)s) = 120
7s + 78 - (21/6)s = 120
7s + 78 - (7/2)s = 120
(7/2)s + 78 = 120
subtract 78 from both sides to isolate s and its coefficient
(7/2)s = 42
multiply both sides by 2/7 to isolate s
12 = s
26 - (7/6)s = c
26 - 14 = c = 12
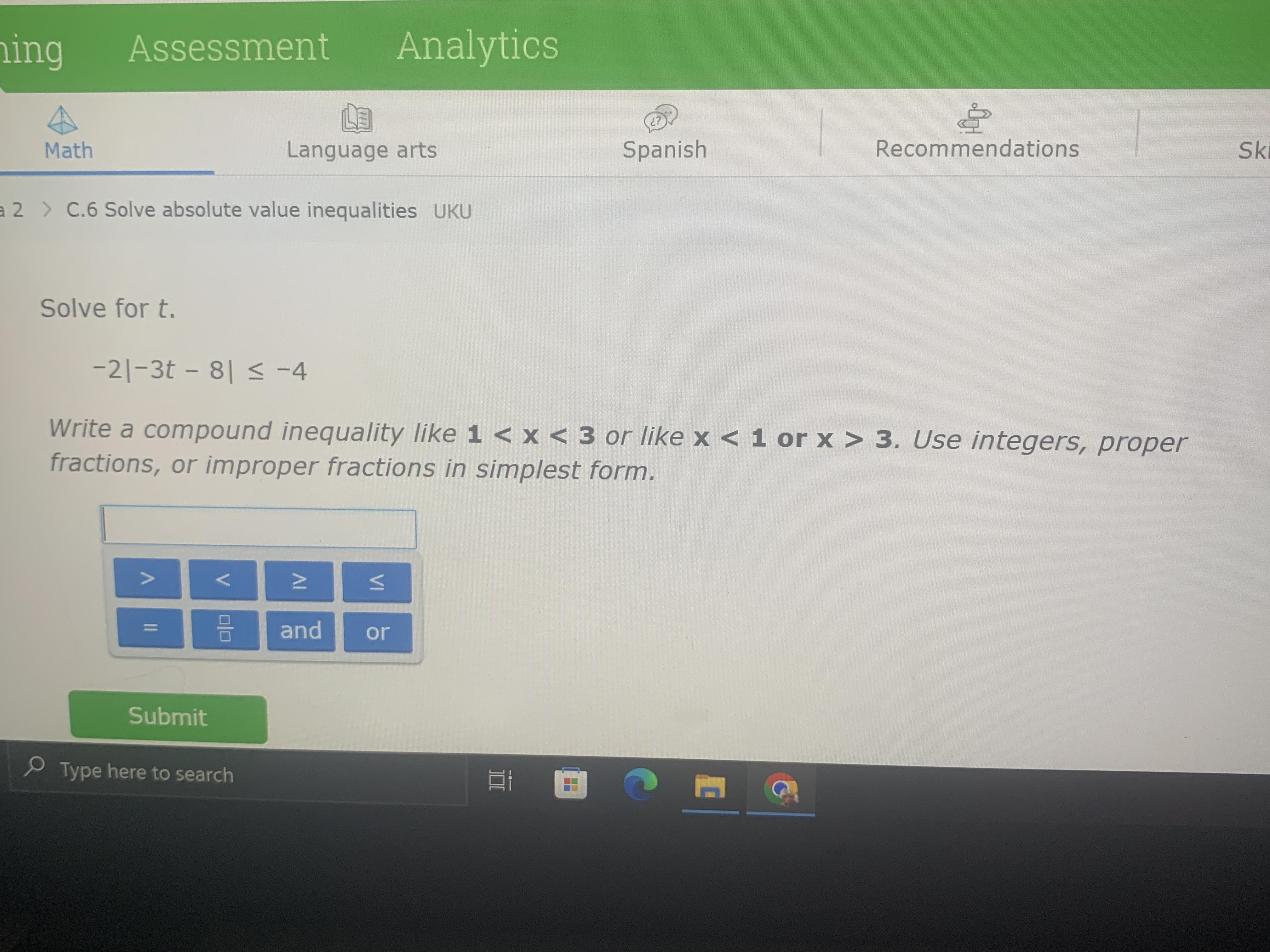
solve for T. pls help this is literally the last one i need to finish
Answers
The solution of the given linear inequality will be -10/3 <= t <= -2.
What are linear inequalities?
Inequality represents the mathematical expression in which both sides are not equal. If the relationship makes the non-equal comparison between two expressions or two numbers, then it is known as inequality in Maths. In this case, the equal sign “=” in the expression is replaced by any of the inequality symbols such as greater than symbol (>), less than symbol (<), greater than or equal to symbol (≥), less than or equal to symbol (≤) or not equal to symbol (≠). The different types of inequalities in Maths are polynomial inequality, rational inequality, absolute value inequality.
The symbols ‘<‘ and ‘>’ express the strict inequalities and the symbols ‘≤’ and ‘≥’ denote slack inequalities. A linear inequality seems exactly like a linear equation but there is a change in the symbol that relates two expressions.
e.g. y>x+2
Now,
Given inequality is -2 I-3t-8I <=-4
So there are two inequalities 1. -2+3t+8<=-4 2. -2-3t-8<=-4
1. 3t+6<=-4 2.-3t-10<=-4
1. t>=-10/3 2. t<=-2
Hence,
The solution of the given linear inequality will be -10/3 <= t <= -2.
To know more about linear inequalities visit the link
https://brainly.com/question/11897796?referrer=searchResults
#SPJ1
Please help! (Also show work)
Tutorials :D

Answers
The five-number summary is:
Minimum: 9
First Quartile: 16.5
Median: 25.5
Third Quartile: 39
Maximum: 51
3. Range = 42
4. Interquartile range = 22.5
How to Find the Five-number Summary of a Data?Given the data for the lengths as, 36, 15, 9, 22, 36, 14, 42, 45, 51, 29, 18, 20, to find the five-number summary of the data set, we would follow the steps below:
1. The numbers in ordered from the smallest to the largest would be:
9, 14, 15, 18, 20, 22, 29, 36, 36, 42, 45, 51
2. The five-number summary for the lengths in minutes would be:
Minimum value: this is the smallest lengths, which is 9First Quartile (Q1): this is the middle of the first half of the data set of the lengths in minutes, which is 16.5.Median: the median is the center of the data distribution which is 25.5.Third Quartile: this is the middle of the second half of the data set of the lengths in minutes, which is 39.Maximum: this is the largest length in minutes, which is, 51.3. Range of the data = max - min = 51 - 9 = 42
4. The interquartile range for the data set = Q3 - Q1 = 39 - 16.5
Interquartile range for the data set = 22.5
Learn more about the five-number summary on:
https://brainly.com/question/24809873
#SPJ1
Which inequality is true if p = 3. 4?
Here are the answer choices
F. 3p < 10. 2
G. 13. 6 ≤ 3. 9p
H. 5p > 17. 1
J. 8. 5 ≥ 2. 5p
pls help!!!
Answers
the inequality that is true when p = 3.4 is J. 8.5 ≥ 2.5p.
To determine which inequality is true when p = 3.4, we can substitute the value of p into each inequality and see which one holds true.
Given:
p = 3.4
F. 3p < 10.2
Substituting p = 3.4:
3 * 3.4 < 10.2
10.2 < 10.2
This inequality is not true.
G. 13.6 ≤ 3.9p
Substituting p = 3.4:
13.6 ≤ 3.9 * 3.4
13.6 ≤ 13.26
This inequality is not true.
H. 5p > 17.1
Substituting p = 3.4:
5 * 3.4 > 17.1
17 > 17.1
This inequality is not true.
J. 8.5 ≥ 2.5p
Substituting p = 3.4:
8.5 ≥ 2.5 * 3.4
8.5 ≥ 8.5
This inequality is true.
Therefore, the inequality that is true when p = 3.4 is J. 8.5 ≥ 2.5p.
Learn more about Inequality here
https://brainly.com/question/20383699
#SPJ4
How do you do these?

Answers
Answer:
a. 10^- 3
b. 10^- 7
c. 10^- 8
d. 10^- 9
e. 1 / 10^6
a.
1 / 10. 1 / 10. 1 / 10
= 1 / ( 10 x 10 x 10 )
= 1 / 1000
= 1 / 10^3
= 10^- 3
b.
1 / 10. 1 / 10. 1 / 10. 1 / 10. 1 / 10. 1 / 10. 1 / 10
= 1 / ( 10 x 10 x 10 x 10 x 10 x 10 x 10 )
= 1 / 10000000
= 1 / 10^7
= 10^- 7
c.
( 1 / 10. 1 / 10. 1 / 10. 1 / 10. )^2
= ( 1 / 1000 )^2
= ( 1 / 10^3 )^2
= ( 10^- 3 )^2
= 10^( - 3 x 2 )
= 10^- 6
d.
( 1 / 10. 1 / 10. 1 / 10 )^3
= ( 1 / 1000 )^3
= ( 1 / 10^3 )^3
= ( 10^- 3 )^3
= 10^( - 3 x 3 )
= 10^- 9
e.
( 10. 10. 10. )^- 2
= ( 10^3 )^- 2
= ( 1 / 10^3 )^2
= 1 / 10^( 3 x 2 )
= 1 / 10^6
Which box plot correctly displays the data set shown below?2, 5, 7, 2, 11, 13,5,7, 1, 10, 10, 2, 3, 5, 1, 11

Answers
Given the data set:
2, 5, 7, 2, 11, 13, 5, 7, 1, 10, 10, 2, 3, 5, 1, 11
Let's find the box plot that correctly displays the data set shown.
In the Diagram segment ad bisects angle bac

Answers
Since segment AD bisects angle BAC, the value of x is equal to 14.6.
What is an angle bisector?In Mathematics, an angle bisector can be defined as a type of line, ray, or segment, that bisects or divides a line segment exactly into two (2) equal angles.
By applying the angle bisector theorem to this triangle (ΔABC), we have:
AB/BD = AC/DC
19/x = 17/(20 - x)
17x = 19(20 - x)
17x = 380 - 19x
19x + 17x = 380
26x = 380
x = 380/26
x = 14.6.
In conclusion, we can reasonably infer and logically deduce that the value of x in triangle ABC is 14.6.
Read more on angle bisector here: brainly.com/question/18714022
#SPJ1
I need help ASAP or before 3:06

Answers
The exponential equation that represents the function is 3x².
What is the equation of the function?The finite difference between two consecutive values of f(x) is given by:
Δf(x) = f(x+1) - f(x)
Δf(-6) = f(-5) - f(-6) = 75 - 108 = -33
Δf(-5) = f(-4) - f(-5) = 48 - 75 = -27
Δf(-4) = f(-3) - f(-4) = 27 - 48 = -21
Δf(-3) = f(-2) - f(-3) = 12 - 27 = -15
The second finite differences are:
Δ²f(-6) = Δf(-5) - Δf(-6) = 6
Δ²f(-5) = Δf(-4) - Δf(-5) = 6
Δ²f(-4) = Δf(-3) - Δf(-4) = 6
Since the second finite differences are constant, the function is a quadratic polynomial of the form;
f(x) = ax² + bx + c
f(-6) = 108 = 36a - 6b + c
f(-5) = 75 = 25a - 5b + c
f(-4) = 48 = 16a - 4b + c
The final equation becomes;
36a - 6b + c = 108 ---- (1)
25a - 5b + c = 75 ------ (2)
16a - 4b + c = 48 -------- (3)
solve the equation, using crammers rule,
a = 3, b = 0, c = 0
f(x) = 3x²
Learn more about quadratic equation here: https://brainly.com/question/28038123
#SPJ1
Find the midpoint, M, of AB.
M
B
.
Too
[?]
22
Answers
Answer:
11 ?
Step-by-step explanation:
your question is a little bit strange and it's hard to understand, but the midpoint you need to find like this: AB/2 22/2=11
30 POINTS!! Select from the drop-down menus to correctly complete the statement. The x-axis is the Choose... axis and the y-axis is the Choose... axis.
Answers
Answer:
add more info
Step-by-step explanation:
For Valentine's Day, Robert and Daniel gave away roses at a park. Robert had 80 roses and gave away 2 roses per minute. Daniel had 120 roses and gave away 4 roses per minute. How long did it take for Robert and Daniel to have the same amount of roses left?
F. 15 minutes
G. 20 minutes
H. 25 minutes
J. Not here
Answers
Step by step:
Solve this and Include work, I need a refresher I forgot how to do this.

Answers
Answer:
X = 20
Step-by-step explanation:
This is an example of a supplementary angle.
A supplementary angle adds up to 180 degrees.
Therefore, in order to find x in this situation you will have to put both angles (added) equal to 180, like this:
5x + 80 = 180
Now, it is simple algebra from here. Solve for x:
5x = 100
x = 20
In conclusion, x is equal to 20.
I hope this helps!!
If you have any questions let me know!
- Kay :)
Answer:
X=20
Step-by-step explanation:
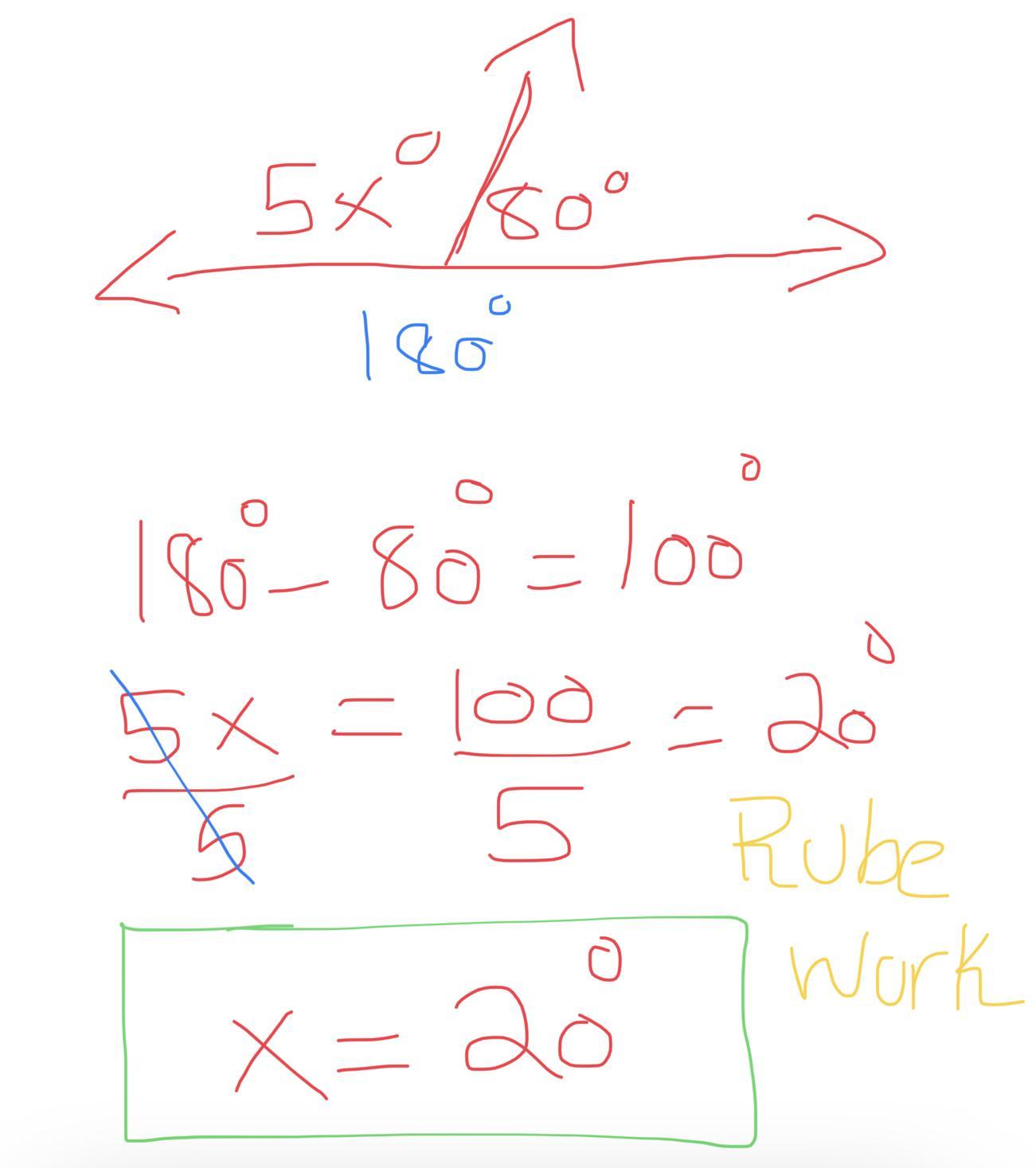
Evaluate the integral below by interpreting it in terms of areas. In other words, draw a picture of the region the integral represents, and find the area using high school geometry.
\int_{-5}^{5} \sqrt{25 - x^2 }dx
Answers
To evaluate the integral \[\int_{-5}^{5} \sqrt{25 - x^2 }dx\] in terms of areas, we need to interpret it as the area of a certain region. First, we note that the integrand $\sqrt{25 - x^2}$ represents the radius of a semicircle centered at the origin with radius 5. Thus, the integral represents the area of the region bounded by the $x$-axis and the upper half of the semicircle.
To find this area, we can split it up into infinitesimally small rectangles of width $dx$, each with height $\sqrt{25 - x^2}$. The area of each rectangle is given by $dA = \sqrt{25 - x^2} dx$. Summing up these infinitesimal areas from $x = -5$ to $x = 5$, we get the total area of the region as: \[\int_{-5}^{5} \sqrt{25 - x^2 }dx = \int_{-5}^{5} dA = A.\]
To compute this integral, we can use the substitution $x = 5\sin(\theta)$, which gives $dx = 5\cos(\theta) d\theta$. Also note that when $x = -5$, we have $\theta = -\frac{\pi}{2}$ and when $x = 5$, we have $\theta = \frac{\pi}{2}$. Thus, we can rewrite the integral as: \[\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (25\cos^2(\theta)) d\theta.\]
Using the trig identity $\cos^2(\theta) = \frac{1+\cos(2\theta)}{2}$, we can simplify the integral as: \[\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (25\cos^2(\theta)) d\theta = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{25}{2} (1+\cos(2\theta)) d\theta.\]
Evaluating the integral gives: \[\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{25}{2} (1+\cos(2\theta)) d\theta = \left[\frac{25}{2}\left(\theta + \frac{1}{2}\sin(2\theta)\right)\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} = \frac{25}{2}(\pi - (-\pi)) = \boxed{\frac{25}{2}\pi}.\] Thus, the integral evaluates to $\frac{25}{2}\pi$, which represents the area of the region bounded by the $x$-axis and the upper half of the semicircle centered at the origin with radius 5.
To evaluate the integral ∫[-5, 5] √(25 - x²) dx by interpreting it in terms of areas, follow these steps:
1. Identify the function: The given function is f(x) = √(25 - x²).
2. Visualize the graph: The graph of this function represents the top half of a circle with radius 5, centered at the origin (0,0).
3. Determine the region of interest: Since the integral is over the interval [-5, 5], the region of interest is the entire top half of the circle.
4. Calculate the area: As this region is a semicircle (half of a circle), we can use the area formula for a circle (A = πr²) to find the area of the semicircle.
Area of the semicircle = (1/2) * π * r² = (1/2) * π * 5² = (1/2) * π * 25 = (25/2)π
So, the integral ∫[-5, 5] √(25 - x²) dx, when interpreted in terms of areas, represents the area of the top half of a circle with radius 5. The area of this region is (25/2)π square units.
The given integral represents the area of a semicircle with radius 5. Thus, the value of the integral is equal to half the area of a circle with radius 5, which is 12.5π or approximately 39.27.
The integral\(\int_{-5}^{5} \sqrt{25 - x^2 }dx\) represents the area between the x-axis and the curve\(y = \sqrt{25 - x^2}\)for x ranging from -5 to 5. This curve is the top half of a circle with radius 5 centered at the origin. To find the area of this semicircle, we can divide it into infinitely many narrow strips of width dx and height\(\sqrt{25 - x^2}\). The area of each strip is approximately \(\sqrt{25 - x^2} dx\), and the total area of the semicircle is obtained by summing up the areas of all such strips, which gives:
Area of semicircle = \(\int_{-5}^{5} \sqrt{25 - x^2} dx\)
This integral can be evaluated using a trigonometric substitution or by using the formula for the area of a circle, which is\(A = \pi r^2\). Since the given semicircle has radius 5, its area is half the area of the corresponding circle, which is 25π. Therefore, the value of the integral is:
\(\int_{-5}^{5} \sqrt{25 - x^2} dx = \frac{1}{2} (25\pi) = 12.5\pi\) approx 39.27.
Learn more about semicircle here: https://brainly.com/question/29140521
#SPJ11
How many solutions does the following system of linear equations have?
6(x + 4) = 2(3x + 4)
Answers
6x + 24 = 6x + 8
Cancel equal terms
24=8
the statement is false(Ø)
Question Content Area
Net Present Value
A project has estimated annual net cash flows of $15,000 for ten
years and is estimated to cost $47,500. Assume a minimum acceptable
rate of return of 20%. Use
Answers
The required rate of return (or minimum acceptable rate of return) is 20 percent. If the net cash flows are $15,000 per year for ten years, the total cash flow is $150,000. The project's cost is $47,500. We can now apply the net present value formula to determine whether or not the project is feasible.
Net Present Value (NPV) = Cash flow / (1 + r)^n - Cost Where, r is the discount rate, n is the number of years, and Cost is the initial outlay.
Net Present Value = 150000 / (1 + 0.20)^10 - 47500
Net Present Value = $67,482.22
Since the NPV is positive, the project is feasible. When calculating net present value, it's important to remember that a positive NPV implies that the project is expected to generate a return that exceeds the cost of capital, whereas a negative NPV indicates that the project is expected to generate a return that is less than the cost of capital, and as a result, it should be avoided.
Know more about NPV here:
https://brainly.com/question/32720837
#SPJ11
Find the maximum and minimum values achieved by f(x) =x3 − 9x2 + 15x + 18 on the interval [0,6]
Answers
The maximum value achieved by f(x) on the interval [0,6] is 21, which occurs at x=3. The minimum value is -12, which occurs at x=0 and x=6.
To find these values, we take the derivative of f(x), set it equal to zero, and solve for x. We then plug in the values of x and evaluate f(x) to find the corresponding maximum and minimum values.
Since the derivative is positive to the left of x=3 and negative to the right, we know that we have a maximum value at x=3.
Similarly, since the derivative is negative to the left of x=0 and positive to the right of x=6, we know that we have minimum values at x=0 and x=6. The graph of f(x) also confirms these results.
To know more about derivative click on below link:
https://brainly.com/question/25324584#
#SPJ11
identify the domain of the function shown in the graph.
A. x is all real numbers
B. 0<x<5
C. -5<x<5
D. x>0

Answers
Answer:
A, all real numbers
Step-by-step explanation:
The domain is the x value and the x value is the domain.
So when you take a look at the x values, it keeps going on and on
So when x values or y values keep going on forever we call that all real numbers
Hope this helps! Plz mark brainliest!
Which one is the right one? Help me please.

Answers
Answer:
90 km/h
Step-by-step explanation:
To solve this problem you first need to convert minutes to hours since the unit is km/h. Doing this we get half an hour (1 hour=60 mins so you divide 30 by 60) after converting you simply divide 45 by 1/2 or .5 to get the answer.
Julia owns a food truck that sells tacos and burritos. She only has enough supplies to make 67 tacos or burritos. She sells each taco for $3.75 and each burrito for $6. Julia must sell no less than $330 worth of tacos and burritos each day. If 42 burritos were sold, determine all possible values for the number of tacos that Julia must sell in order to meet the requirements. Your answer should be a comma separated list of values. If there are no possible solutions, submit an empty answer.
Answers
The point would be the solution (25,40).
Let
The number of tacos sold is represented by x.
x denotes the quantity of burritos sold.
We are aware of this,
⇒ x + y 62
⇒ 3.75x + 6y = 330
The triangle shaded region is the answer
(25,40)
The point is one possible solution (25,40).
Remember that if an ordered pair is a solution to a system of inequalities, then the ordered pair must reside on the solution's region.
That indicates there were 30 tacos sold and 30 burritos sold.
Learn more about inequality at
https://brainly.com/question/25977724
#SPJ1
Rain is falling steadily in Seattle, Washington. After 6 hours, 4 inches of rain has fallen. How many inches of rain will fall in 9.5 hours?
Answers
Answer:
6.3333333
Step-by-step explanation:
6 = 4
9.5=X
cross multiply
6x=38
Divide both sides by 6
x=6.3333333
Answer: 14.25 inches in 9.5 hours.
Step-by-step explanation:
The rate of inches per hour is 1.5. In 9.5 hours, this would add up to 14.25 inches.
A motorboat is capable of traveling at a speed of 10 miles per hour in still water. On a particular day, it took 10 minutes longer to travel a distance of 4 miles upstream than it took to travel the same difference downstream. What was the rate of the current in the stream on that day?
The rate of the current was ______ mph on that day.
Answers
The rate of the current in the stream was 6 mph.
What is the distance?Distance is defined as the product of speed and time.
Let's assume the speed of the current "c" and the time it takes the boat to travel upstream "t". We can then set up the following two equations:
Upstream: 4/(10-c) = t
Downstream: 4/(10+c) = t - 10
We can then solve for c by substituting the value of t from the first equation into the second equation and solving for c. This gives us:
4/(10-c) = t
4/(10+c) = t - 10
4/(10+c) = (10-c)/(10-c)
4 = 10 - c
c = 6
Thus, the rate of the current in the stream on that day was 6 miles per hour.
Learn more about the distance here:
brainly.com/question/13269893
#SPJ1
Demand and Consumer Surplus: Joe's demand for pizza can be described with this function: Q = 30 - 2P where Q is the number of slices of pizza consumed per week and Pis the price of a slice. a. Plot the demand curve, with P on the vertical axis and on the horizontal axis. Label the vertical and horizontal intercepts (5 points). b. Joe's total spending on pizza at P = 5 equals 20*5 = 100. His total spending on pizza at P=4 is 22*4 = 88. Without calculating the elasticity of demand directly, what do these total spending figures tell you about Joe's elasticity of demand for pizza between P= 5 and P=4? Explain. (5 points) c. Suppose P=9. Calculate Joe's consumer surplus at this price. (5 points) d. Suppose a rise in the price of tomatoes results in pizza prices rising to $15 (!) per slice. What is Joe's consumer surplus at this new price? (5 points)
Answers
The total spending figures indicate that Joe's demand for pizza is elastic as his total spending decreases when the price decreases, suggesting he is responsive to price changes.
What is the interpretation of Joe's total spending figures for pizza at different prices?a. The demand curve for Joe's pizza can be plotted by using the equation Q = 30 - 2P, where Q represents the quantity of pizza consumed and P represents the price per slice.
On the graph, the vertical axis represents the price (P), and the horizontal axis represents the quantity (Q). The vertical intercept occurs when Q is 0, which corresponds to P = 15. The horizontal intercept occurs when P is 0, which corresponds to Q = 30.
b. The total spending on pizza at P = 5 is $100, and the total spending at P = 4 is $88. This information indicates that Joe's total spending decreases as the price of pizza decreases.
Based on this, we can infer that Joe's elasticity of demand for pizza between P = 5 and P = 4 is elastic. When the price decreases from $5 to $4, the total spending decreases, indicating that the demand is responsive to price changes.
c. When P = 9, we can substitute this value into the demand function to calculate the corresponding quantity: Q = 30 - 2(9) = 30 - 18 = 12. To calculate Joe's consumer surplus, we need to find the area of the triangle formed by the demand curve and the price line.
The consumer surplus is given by (1/2) ˣ (9 - P) ˣ Q = (1/2) ˣ (9 - 9) ˣ 12 = 0.d. If the price of pizza rises to $15 per slice, we can again substitute this value into the demand function to find the corresponding quantity: Q = 30 - 2(15) = 30 - 30 = 0.
Joe's consumer surplus at this new price would be zero since he is not consuming any pizza at that price, resulting in no surplus.
Learn more about Joe's
brainly.com/question/31536415
#SPJ11
a strain of bacteria growing on your desktop doubles every 5 minutes. assuming that you start with only one bacterium, how many bacteria could be present at the end of 96 minutes?
Answers
Since the strain of bacteria doubles every 5 minutes, we can use the exponential growth formula to calculate the number of bacteria present at any given time. The formula is given by:
N = N0 * 2^(t/d)
where:
N = final number of bacteria
N0 = initial number of bacteria (1 in this case)
t = time elapsed (96 minutes)
d = doubling time (5 minutes)
Plugging in the values into the formula:
N = 1 * 2^(96/5)
Using a calculator or simplifying the exponent:
N ≈ 1 * 2^19.2
Since we're dealing with whole numbers, we can round the exponent to the nearest whole number:
N ≈ 1 * 524,288
Therefore, at the end of 96 minutes, there could be approximately 524,288 bacteria present.
To learn more about exponential : brainly.com/question/29160729
#SPJ11
