Find a value for y for which the expression (1-y)(3-y)(6-y) has each given value
i. -70
ii. 120
Answers
\(\\ \tt\Rrightarrow (1-y)(3-y)(6-y)=-70\)
\(\\ \tt\Rrightarrow -y(1+1)(3+1)(6+1)=-70\)
\(\\ \tt\Rrightarrow y(2)(4)(7)=70\)
\(\\ \tt\Rrightarrow y(56)=70\)
\(\\ \tt\Rrightarrow y=\dfrac{70}{56}\)
\(\\ \tt\Rrightarrow y=\dfrac{5}{4}\)
#2
\(\\ \tt\Rrightarrow (1-y)(3-y)(6-y)=120\)
\(\\ \tt\Rrightarrow -y(1+1)(3+1)(6+1)=120\)
\(\\ \tt\Rrightarrow -y(2)(4)(7)=120\)
\(\\ \tt\Rrightarrow 56y=-120\)
\(\\ \tt\Rrightarrow y=\dfrac{-120}{56}\)
\(\\ \tt\Rrightarrow y=\dfrac{-15}{7}\)
Answer:
i. y = 8, ii. y = -2Step-by-step explanation:
(1 - y)(3 - y)(6 - y) = -70We can see the divisors are 2 and 3 apart.
i.
Factorize -70 so that divisors are 2 and 3 apart:
- 70 = (- 2)*(- 5)*(- 7)The smallest one is 1 - y and -7:
1 - y = -7y = 1 + 7 y = 8ii
Factorize 120 so that divisors are 2 and 3 apart:
120 = 3*5*8The smallest one is 1 - y and 3:
1 - y = 3y = 1 - 3y = -2Related Questions
PLzzz help me!! Stuck with this equation

Answers
Answer:
f(2) = 15
for f(x) = 4, x = 6
Step-by-step explanation:
f(2) means f(x) for x = 2.
in the table for x = 2 we see f(x) = 15.
the second question : f(x) = 4
so, where in the table do we find f(x) = 4 ? ah, for x = 6 do we find f(x) = 4.
At a football game, a vender sold a combined total of 213 sodas and hot dogs. The number of hot dogs sold was 51 less than the number of sodas sold. Find the number of sodas sold and the number of hot dogs sold.
Answers
Explanation:
Let x be the number of hot dog sold
Let y be the number of soda sold
x + y = 213
And x = y - 51
Substitute x value in the first equation:
y - 51 + y = 213
2y = 264
y = 132
Find x:
x + 132 = 213
X = 213 - 132
x = 81
Therefore, the number of hotdog sold was 81
The number of soda sold was 132
Covert, how many lb. If = 3,200 oz
Answers
Answer:
200 lbs.
Step-by-step explanation:
Divide mass value by 16 to convert oz to lbs.
3,200/16=200
6. A company car purchased for $39,600 depreciates at 12% per annum. What is the car
worth after 3 years?
Answers
Answer:
$26,986.29
Step-by-step explanation:
We can use the formula for calculating the depreciation of an asset over time:
wor
\(\bold{D = P(1 - \frac{r}{100} )^t}\)
where:
D= the current value of the asset
P = the initial purchase price of the asset
r = the annual depreciation rate as a decimal
t = the number of years the asset has been in use
In this case, we have:
P = $39,600
r = 12% = 0.12
t = 3 years
Substituting these values into the formula, we get:
\(D= 39,600(1 - \frac{12}{100})^3\\D= 39,600(1 - 0.12)^3\\D= 39,600*0.88^3\\D= 39,600*0.681472\\D=26986.2912\)
Therefore, the car is worth approximately $26,986.29 after 3 years of depreciation at a rate of 12% per annum.
Answer:
$26,986.29
Step-by-step explanation:
As the car's value depreciates at a constant rate of 12% per annum, we can use the exponential decay formula to create a function for the value of the car f(t) after t years.
Exponential Decay formula\(\boxed{f(t)=a(1-r)^t}\)
where:
f(t) is the value of the car (in dollars) after t years.a is the initial value of the car.r is the depreciation rate (as a decimal).t is the time period (number of years after purchase).In this case, the initial value is $39,600, and the rate of depreciation is 12% per year. Therefore, the function that models the value of the car after t years is:
\(f(t)=39600(1-0.12)^t\)
\(f(t)=39600(0.88)^t\)
To calculate the value of the car after 3 years, substitute t = 3 into the function:
\(\begin{aligned} f(3)&=39600(0.88)^3\\&=39600(0.681472)\\&=26986.2912\\&=26986.29\;(\sf 2\;d.p.)\end{aligned}\)
Therefore, the car is worth $26,986.29 after 3 years.
If every 2 cm on a scale drawing is equal to 7 feet in real life, which lines on the drawing would be greater than 21 feet in real life? Select all that apply. A) 7 cm B) 5 cm C) 9 cm D) 12 cm
Answers
The correct answers are A) 7cm, C) 9cm and D) 12cm
Define the Conversion of units?The process of changing a given quantity that is expressed in one unit of measurement to another unit of measurement that is equivalent in value is referred to as conversion of units.
If every 2 cm on a scale drawing is equal to 7 feet in real life, then we can use proportions to find out which lines on the drawing would be greater than 21 feet in real life.
Let x be the length of a line on the scale drawing in centimeters. Then, we can set up the following proportion:
⇒ \(\frac{2cm}{7 feet} = \frac{x cm }{yfeet}\)
where y is the length of the line in real life. Solving for y, we get:
⇒ \(y = \frac{7 feet} {2cm} *x\)
⇒ \(y = 3.5 x feet\)
If we put x = 2cm (given) then, y = 7 feet
For y = 21 feet, the value of x = 6cm.
Therefore, any line on the scale drawing that is greater than 6cm in length corresponds to a length greater than 21 feet in real life.
So, the lines on the drawing that are greater than 21 feet in real life are:
A) 7cm, C) 9cm, D) 12cm
Therefore, the correct answers are A) 7cm, C) 9cm and D) 12cm
To know more about conversion, visit:
https://brainly.com/question/13016491
#SPJ1
PLS HELPPPPPPPPPPPPPPOOP

Answers
The blue object (D) has been rotated 270° clockwise about the point (1, 2). Which is the correct image?

Answers
The correct image include the following: B. Green: image A.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation which moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
By applying a rotation of 270° clockwise about the point (1, 2) to the coordinate of the vertices of blue block D, the coordinate the vertices of of its image would be located at the position of the Green: image A.
In this context, we can reasonably infer and logically deduce that Green: image A is the correct transformed shape.
Read more on rotation here: brainly.com/question/28854313
#SPJ1
Write the following expression in simplest form.
the expression quantity negative three fifths times x minus 7 end quantity minus quantity negative 12 plus three tenths times x end quantity
negative nine tenths times x plus 5
negative nine tenths times x plus negative 5
three over 10 times x plus 5
three over 10 times x plus negative 19
Answers
The following expression (-3/5)x-7-(-12)+(3/10)x can be written in the simplest form as -3/10x+5( three over 10 times x plus 5). So, option c is correct.
What is meant by an expression?An expression or mathematical expression is a finite arrangement of symbols that are well-formed in line with context-dependent criteria. To help define the logical grammar and order of operations, mathematical symbols can be used to represent variables, operations, functions, brackets, punctuation, and grouping. A sentence qualifies as a mathematical expression if it comprises one or more mathematical operations, at least two numbers, or variables. Mathematicians have the ability to multiply, divide, add, and subtract. The following is the structure of an expression: Expression, number/variable, and mathematical operator.
(-3/5)x-7-(-12)+(3/10)x
-3/5x-7+12+3/10x
-6/10x-7+12+3/10x
-3/10x+5
Three over 10 times x plus 5
Therefore, the following expression (-3/5)x-7-(-12)+(3/10)x can be written in the simplest form as -3/10x+5( three over 10 times x plus 5).
Hence, option c is correct.
To know more about expression, visit:
https://brainly.com/question/1859113
#SPJ1
I don’t know how to do it

Answers
\(\begin{array}{llll} \textit{Logarithm of exponentials} \\\\ \log_a\left( x^b \right)\implies b\cdot \log_a(x) \end{array} ~\hspace{7em} \begin{array}{llll} \textit{logarithm of factors} \\\\ \log_a(xy)\implies \log_a(x)+\log_a(y) \end{array} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\log(x)=2\hspace{5em}\log(y)=3\hspace{4em}\log(2)\approx 0.3\hspace{4em}\log(3)\approx 0.48 \\\\[-0.35em] ~\dotfill\\\\ \log\left(\sqrt[3]{x^4\cdot y^2} \right)\implies \log\left(\left( x^4\cdot y^2 \right)^{\frac{1}{3}} \right)\implies \cfrac{1}{3}\log(x^4 y^2) \\\\\\ \cfrac{1}{3}[\log(x^4)~~ + ~~\log(y^2)]\implies \cfrac{1}{3}[4\log(x)~~ + ~~2\log(y)]\implies \cfrac{1}{3}[4(2)~~ + ~~2(3)] \\\\\\ \cfrac{1}{3}[8~~ + ~~6]\implies {\Large \begin{array}{llll} \cfrac{14}{3} \end{array}}\)
Given
Principal 1500
Intrest 6%
Time 240 days
Partial payments for 100th day 7,000
For 180th day 4,000
A. Use the u.s rule to solve for total intrest cost
B. Use the u.s rule to solve the balance after payments for the 100th and 180th
C use the u.s rules to solve final payment
Answers
If s(x) = 2x² and f(x) = 3x, which value is equivalent to (s-f)(-7)?
O-439
O-141
O 153
O 443
Answers
The value of expression (s - f) (- 7) would be,
⇒ (s - f) (- 7) = 119
We have to given that,
Functions are defined as,
⇒ s (x) = 2x²
⇒ f (x) = 3x
Now, We can find the value of (s - f) (- 7) is,
⇒ (s - f) (- 7)
⇒ s (- 7) - f (- 7)
⇒ 2 (- 7)² - (3 × - 7)
⇒ 2×49 + 21
⇒ 98 + 21
⇒ 119
Therefore, The value of expression (s - f) (- 7) would be,
⇒ (s - f) (- 7) = 119
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ1
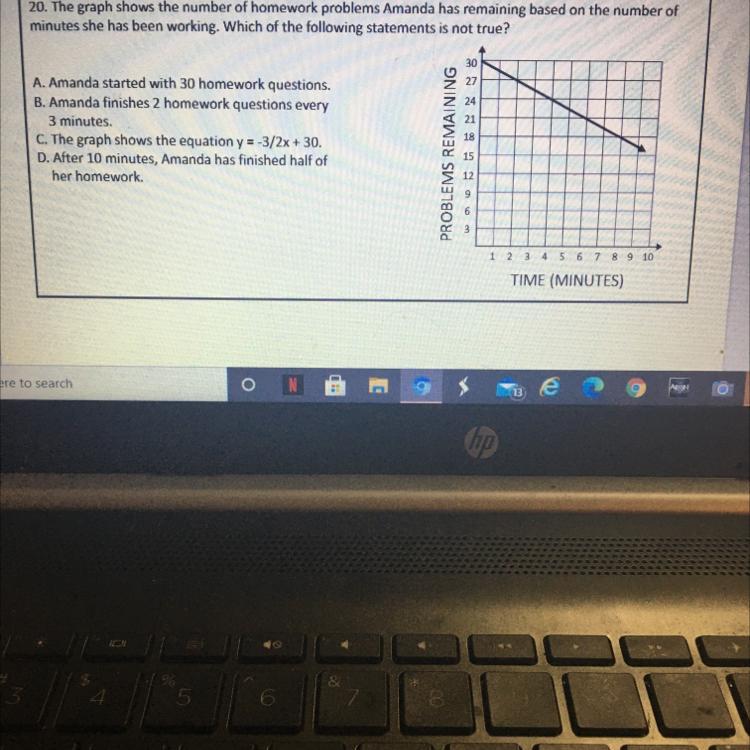
20. The graph shows the number of homework problems Amanda has remaining based on the number ofminutes she has been working. Which of the following statements is not true?30272421A. Amanda started with 30 homework questions.B. Amanda finishes 2 homework questions every3 minutes.C. The graph shows the equation y = -3/2x + 30.D. After 10 minutes, Amanda has finished half ofher homework.18PROBLEMS REMAINING15121 2 3 4 5 6 7 8 9 10TIME (MINUTES)
Answers
B is not true, because in the graph when x=0 y=30, and when x=3 y is not equal to 28 (that would be true if she finishes 2 homework points every 3 minutes). the final answer will be B
Suppose it takes John 10 minutes to run1 mile. How long would it take if he to run 4 kilometers
Answers
Evidence; 4 kilometers is 2.49 miles so 10•2=20
0.49 miles left so what we would do here is 0.1 mile is 1 minute so 0.01 mile is 10 seconds so 0.09 miles would be 90 seconds, and 90 seconds is 1 min and a half so thats 20+4+1.30=25.3
pls mark as brainlist if possible!
if you take away 25 from a number you will be left with two and halftimes 30. what is the number?
Answers
If you take away 25 from (100) you get 75.
70 also equals 2.5*30
Please help!!!!!!!!!!!!

Answers
The calculated values of the sum of interior angles of the shapes are 1080 degrees and 360 degrees
Calculating the sum of interior angles of the shapesThe formula of the sum of interior angles of a polygon is
Sum = (n − 2) * 180
For the octagon, we have
n = 8
This means that
Sum of angles = (8 − 2) * 180
Evaluate
Sum of angles = 1080
For the square, we have
n = 4
This means that
Sum of angles = (4 − 2) * 180
Evaluate
Sum of angles = 360
Hence, the sum of interior angles of the shapes are 1080 degrees and 360 degrees
Read more about polygon at
https://brainly.com/question/8409681
#SPJ1
NO LINKS!! URGENT HELP!!
Calculate the perimeter of the following figures.

Answers
Answer:
Quadrilateral: 20.5 units
Triangle: 8.6 units
Step-by-step explanation:
Quadrilateral:
We can use the following formula to find the perimeter of a quadrilateral.
Perimeter = AB + BC + CD + DA
where AB, BC, CD, and DA are the lengths of the four sides of the quadrilateral.
In your case, the coordinates of the vertices of the quadrilateral are A(-3,-1), B(-3,3), C(2,3), and D(4,-1).
Using the distance formula, we can find the lengths of the four sides of the quadrilateral as follows:
\(AB = \sqrt{(-3 - (-3))^2 + ((-1) - 3)^2} = \sqrt{16} = 4\)
\(BC = \sqrt{(-3 - 2)^2 + ((3) - 3)^2} = \sqrt{25}= 5\)
\(CD = \sqrt{(2 - 4)^2 + ((3) - (-1))^2} = \sqrt{4+16} = 2\sqrt{5}\)
\(DA = \sqrt{(4 - (-3))^2 + ((-1) - 1)^2} = \sqrt{49} =7\)
Therefore, the perimeter of the quadrilateral is:
Perimeter = AB + BC + CD + DA
= \(4+5+2\sqrt5+7=20.5\) units
Triangle
The perimeter of a triangle is the total length of all three sides of the triangle. To find the perimeter of a triangle, we can use the following formula:
Perimeter = AB + BC + CA
where AB, BC, and CA are the lengths of the three sides of the triangle.
In your case, the coordinates of the vertices of the triangle are
E(-4,1), F(-2,3), and G(-2,4). Using the distance formula, we can find the lengths of the three sides of the triangle as follows:
\(EF = \sqrt{(-4 - (-2))^2 + ((1) - (3))^2} = 2\sqrt{2}\)
\(FG = \sqrt{(-2 - (-2))^2 + ((3) - (4))^2} = 1\)
\(EG = \sqrt{(-4 - (-2))^2 + ((1) - (4))^2} = \sqrt{4 + 9} = \sqrt{13}\)
Therefore, the perimeter of the triangle is:
Perimeter = EF + FG + EG
= 4 + 1 + \(\sqrt{13}\)
=8.6 units
Therefore, the perimeter of the quadrilateral is 20.5 units and the perimeter of the triangle is 8.6 units


Simplify the following expression.

Answers
Answer:
\(\displaystyle \frac{cd^6}{a^4b^2}\)
Step-by-step explanation:
\(\displaystyle \frac{a^{-4}b^{-2}cd^6}{e^{-7}}\\\\=a^{-4}b^{-2}cd^6e^7\\\\=\frac{cd^6}{a^4b^2}\)
Notice that the variables with negative exponent that were originally in the denominator went to the numerator (like with \(e^{-7}\)) and became positive, and vice versa with those originally in the numerator went in the denominator (like with \(a^{-4}b^{-2}\)) and also became positive.
Step-by-step explanation:
a‐⁴b‐²cd⁶
_______
e‐⁷
cd⁶e⁷
_____
a⁴b²
Solve the literal equation for y. 20=8x+4y
Answers
Answer:
y=2x+5
Step-by-step explanation:
−8x+4y=20
Step 1: Add 8x to both sides.
−8x+4y+8x=20+8x
4y=8x+20
Step 2: Divide both sides by 4.
4y4=8x+204
y=2x+5
Answer:
y=2x+5
Step-by-step explanation:
Let's solve for y.
20=8x+4y
Step 1: Flip the equation.
8x+4y=20
Step 2: Add -8x to both sides.
8x+4y+−8x=20+−8x
4y=−8x+20
Step 3: Divide both sides by 4.
4y
4
=
−8x+20
4
y=−2x+5
PLEEASE HELP ON LAST PROBLEM!! (problem 4)
thank you!

Answers
a. The amount he deposited at first is $975
b. This is a case of exponential growth
c. the monthly interest rate is 0.3%
d. The account balance after 6 months and 12 months are
e. it will take 10months
What is compound interest?Compound interest is the interest you earn on interest. The amount earned or paid is expressed as;
A = p( 1+r/100)^t
where p is the principal and t is the time
Relating the equation ; b = 975(1.003)^m
therefore;
1. The initial amount deposited = $ 975
2. The case is an exponential growth because the balance will be creasing with increase in number of month.
3. The monthly interest rate =
1.003 = 1+r/100
r/100 = 1-1.003
r /100 = 0.003
r = 0.3%
4. the balance after 6 months
975(1.003)^6
= 975 × 1.018
=$ 992.55
after 12 months
= 975(1.003)^12
= $1010.68
5. if b = $1000
1000 = 975(1.003)^m
(1.003)^m = 1000/975
(1.003)^m = 1.03
m = 10 months.
learn more about compound interest from
https://brainly.com/question/24274034
#SPJ1
What is the area of a rectangle with side lengths of 5/12 foot and 2/3 foot?A: 7/36 square footB: 10/36 square footC: 15/24 square footD: 7/15 square foot
Answers
The Area of a Rectangle
A rectangle of width W and length L has an area calculated as:
\(A=W\cdot L\)We are given the side lengths W = 2/3 and L = 5/12. The order of the sides is not important because the area is a product and it's a commutative operation.
Calculating:
\(A=\frac{2}{3}ft\cdot\frac{5}{12}ft\)Multiplying numerators and denominators separately:
\(A=\frac{10}{36}ft^2\)This fraction can be simplified but if we do, we won't be able to find the correct choice, thus:
Area = B: 10/36 square foot
How do you do this question?

Answers
Answer:
7√3 + 7π/6 ≈ 15.790
Step-by-step explanation:
First, find the intersection:
7 cos(2x) = 7 − 7 cos(2x)
14 cos(2x) = 7
cos(2x) = 1/2
2x = π/3
x = π/6
From the graph:
On 0 ≤ x ≤ π/6, 7 cos(2x) > 7 − 7 cos(2x).
On π/6 ≤ x ≤ π/2, 7 − 7 cos(2x) > 7 cos(2x).
So the integral is:
\(\int\limits^\frac{\pi}{6} _0 {[7cos(2x)-(7-7cos(2x))]} \, dx + \int\limits^\frac{\pi}{2} _\frac{\pi}{6} {[(7-7cos(2x))-7cos(2x)]} \, dx\)
\(\int\limits^\frac{\pi}{6} _0 {[7cos(2x)-7+7cos(2x))]} \, dx + \int\limits^\frac{\pi}{2} _\frac{\pi}{6} {[7-7cos(2x)-7cos(2x)]} \, dx\)
\(\int\limits^\frac{\pi}{6} _0 {[14cos(2x)-7]} \, dx + \int\limits^\frac{\pi}{2} _\frac{\pi}{6} {[7-14cos(2x)]} \, dx\)
\([7sin(2x)-7x]|^\frac{\pi}{6} _0 + [7x-7sin(2x)]|^\frac{\pi}{2} _\frac{\pi}{6}\)
\([7sin(\frac{\pi }{3} )-\frac{7\pi }{6} ] - [7sin(0)-0 ] + [\frac{7\pi }{2} -7sin(\pi )] - [\frac{7\pi }{6} -7sin(\frac{\pi }{3} )]\)
\(7sin(\frac{\pi }{3} )-\frac{7\pi }{6} + \frac{7\pi }{2} -7sin(\pi ) - \frac{7\pi }{6} +7sin(\frac{\pi }{3} )\)
\(14sin(\frac{\pi }{3} )-\frac{7\pi }{3} + \frac{7\pi }{2}\)
\(7\sqrt{3} + \frac{7\pi }{6}\)
Approximately 3.2 million cats enter U.S. animal
shelters nationwide every year. There are r million
more dogs that enter than cats. Write an expression to
find how many million dogs are in the animal shelters
nationwide.
Answers
9514 1404 393
Answer:
3.2 +r
Step-by-step explanation:
When r is added to 3.2, the sum is ...
3.2 +r . . . . . . million dogs entering shelters annually
_____
Additional comment
The question asked cannot be answered using the information given in the problem statement. Information is given as to numbers of animals entering shelters. The question asks for the number of animals in shelters. That answer depends on the number leaving, which is not given.
You roll a 6-sided die two times. What is the probability of rolling a 4 and then rolling a 2? (Write your answer as a fraction or whole number.)
Answers
Answer:
1/36
Step-by-step explanation:
On the first throw, the probability of rolling any particular number, 1 through 6, is 1 out of 6. So the chance of rolling a 4 is 1/6.
On the second roll, your probability of rolling a 2 is 1/6.
The 'trick' is knwoing what to do with those two numbers.
Here's the rule: If events are dependent on one another, you multiply the probabilities.
Any time you see a scenario where X has to happen and then some other thing (X, Y, or whatever) has to happen, the events are dependent.
Probability of rolling a 4 and then rolling a 2 = 1/6 * 1/6 = 1/36
Hope this helps.
Can you help please on this

Answers
Answer:
5
Step-by-step explanation:
Which problem can be solved by performing this multiplication?
3/4×8/9
Responses
Evan practiced piano this week for 3/4 hour. Last week he practice for8/9 hour. How much longer did Evan practice last week than this week?
Jada rode her bike 3/4 mile. Sarah rode her bike 8/9 the distance that Jada rode her bike. How far did Sarah ride her bike?
Amelie drove 3/4 mile. She then drove another 8/9 mile. How many miles did she drive in all?
Three out of 4 containers hold lemonade. Each container holds 8/9 quart of lemonade. How much lemonade do the containers all hold?
Answers
The multiplication 3/4×8/9 can be used to address the problem in response (B). which is the correct answer that would be an option (B).
What is the Multiplication operation?In mathematics, Multiplication operations perform Multiplying values on either side of the operator.
For example 4×2 = 8
As per option (B),
Jada rode her bike for 3/4 mile. Sarah rode her bike 8/9 the distance that Jada rode her bike.
Sarah rides her bike = Sarah rode (8/9) of the (3/4) that Jada rode.
Sarah rides her bike = 3/4 × 8/9
Therefore, this problem can be solved by performing the above multiplication.
Hence, the correct answer would be an option (B).
Learn more about Multiplication operations here:
brainly.com/question/25834626
#SPJ1
Write the equation of the line in fully simplified slope-intercept form.
-12-11-10-9-
12
11
10
9
R
5
4
2
654-3-2-1
-2
3
4
-5
-6
-8
6
-10
-11
-12
34567 8 9 10 11 12

Answers
The equation of the line in fully simplified slope-intercept form is y = x + 7.
We have,
From the graph,
The coordinates of the line are:
(0, 7), (-7, 0), and (-2, 5).
We can use any coordinates the line touches on the graph.
We will use,
(0, 7) and (-7, 0)
The equation can be written in the form y = mx + c
m = (0 - 7) / (-7 - 0)
m = -7/-7
m = 1 ______(1)
And,
(0, 7) = (x, y)
So,
y = mx + c ______(2)
7 = 1 x 0 + c
7 = c
c = 7 ______(3)
Now,
From (1), (2), and (3).
y = x + 7
Thus,
The equation of the line in fully simplified slope-intercept form is y = x + 7.
Learn more about equation of a line here:
https://brainly.com/question/23087740
#SPJ1
Nathan works the same number of hours each day five days a week he earns $12 per hour last week and $420 how many hours did you work each day last week
Answers
Answer:
35 days
Step-by-step explanation:
First division the total money
with per hour earn
$420/$12
=35 hour's
35/24
=about 1 hour45 minutes
The perimeter of the TCL 3-Series Roku Smart TV is 112 inches. The width of the TV is 16 inches greater than its height. Find the width and the height of the TV.
Answers
Answer: Height = 20 inches, Width = 36 inches
Step-by-step explanation:
Let the height be \(h\) and the width be \(h+16\).
Using the formula for the perimeter of a triangle,
\(2(h+h+16)=112\\\\2(2h+16)=112\\\\2h+16=56\\\\2h=40\\\\h=20 \implies h+16=36\)
A fancy restaurant put dishes of butter at each table. They divided 4/5 of a kilogram of butter evenly to put 1/5 of a kilogram in each dish. How many butter dishes did they fill?
Answers
Answer: 4
This problem requires basic division. If the restaurant divided 4/5 kg of butter with 1/5 kg on each dish, you would need to compute 4/5 divided by 1/5.
4/5 ÷ 1/5
Using the "KFC" method, or Keep, Change, Flip, you would keep the first number (in this case, 4/5), change the division sign, and flip the fraction to 5/1, or 5. We now have this:
4/5 x 5
To compute this equation, you must multiply the numerators of both of the numbers together. In this case, you would compute (4x5)/5, resulting with 20/5, or 4.
You can check this answer by re-multiplying the numbers together. 1/5 kg of butter per dish, multiplied by the total amount of dishes, 4, you would result in the original 4/5 kg of butter.
Hope this helps!
Determine f of the quantity 3 plus h end quantity minus f of 3 all over h if f (x) = 3x − 2.232h3h
Answers
The given function f(x) is:
\(f(x)=3x-2\)Let's start finding f(4) by replacing x=4:
\(\begin{gathered} f(4)=3\cdot4-2 \\ f(4)=12-2 \\ f(4)=10 \end{gathered}\)Now, find f(4+h) by replacing x=4+h:
\(\begin{gathered} f(4+h)=3\cdot(4+h)-2 \\ f(4+h)=12+3h-2 \\ f(4+h)=10+3h \end{gathered}\)Thus:
\(\begin{gathered} \frac{f(4+h)-f(4)}{h}=\frac{10+3h-10}{h} \\ \Rightarrow\frac{3h}{h} \\ \text{Simplify h/h} \\ \frac{f(4+h)-f(4)}{h}=3 \end{gathered}\)The answer is option b. 3