Find a positive number such that the sum of and is as small as possible. does this problem require optimization over an open interval or a closed interval? a. closed b. open
Answers
To find a positive number such that the sum of and is as small as possible, we need to use optimization. This problem requires optimization over a closed interval. The given problem is as follows, Let x be a positive number. Find a positive number such that the sum of and is as small as possible.
To find a positive number such that the sum of and is as small as possible, we need to use optimization. This problem requires optimization over a closed interval. The given problem is as follows, Let x be a positive number. Find a positive number such that the sum of and is as small as possible. So, we need to minimize the sum of and . Now, let's use calculus to find the minimum value of the sum.To find the minimum value, we have to find the derivative of the sum of and , i.e. f(x) with respect to x, which is given by f '(x) as shown below:
f '(x) = 1/x^2 - 1/(1-x)^2
We can see that this function is defined on the closed interval [0, 1]. The reason why we are using the closed interval is that x is a positive number, and both endpoints are included to ensure that we cover all positive numbers. Therefore, the problem requires optimization over a closed interval. This means that the minimum value exists and is achieved either at one of the endpoints of the interval or at a critical point in the interior of the interval.
To know more about positive number visit: https://brainly.com/question/17887499
#SPJ11
Related Questions
A tank contains 9,000 L of brine with 12 kg of dissolved salt. Pure water enters the tank at a rate of 90 L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. (a) How much salt is in the tank after t minutes? y = kg (b) How much salt is in the tank after 20 minutes? (Round your answer to one decimal place.) y = kg
Answers
Therefore, After 20 minutes, there are approximately 11.9 kg (rounded to one decimal place) of salt in the tank.
To solve this problem, we need to consider the rate of change of the amount of salt in the tank over time.
(a) Let's denote the amount of salt in the tank after t minutes as y (in kg). We can set up a differential equation to represent the rate of change of salt:
dy/dt = (rate of salt in) - (rate of salt out)
The rate of salt in is given by the concentration of salt in the incoming water (0 kg/L) multiplied by the rate at which water enters the tank (90 L/min). Therefore, the rate of salt in is 0 kg/L * 90 L/min = 0 kg/min.
The rate of salt out is given by the concentration of salt in the tank (y kg/9000 L) multiplied by the rate at which water leaves the tank (90 L/min). Therefore, the rate of salt out is (y/9000) kg/min.
Setting up the differential equation:
dy/dt = 0 - (y/9000)
dy/dt + (1/9000)y = 0
This is a first-order linear homogeneous differential equation. We can solve it by separation of variables:
dy/y = -(1/9000)dt
Integrating both sides:
ln|y| = -(1/9000)t + C
Solving for y:
y = Ce^(-t/9000)
To find the particular solution, we need an initial condition. We know that at t = 0, y = 12 kg (the initial amount of salt in the tank). Substituting these values into the equation:
12 = Ce^(0/9000)
12 = Ce^0
12 = C
Therefore, the particular solution is:
y = 12e^(-t/9000)
(b) To find the amount of salt in the tank after 20 minutes, we substitute t = 20 into the particular solution:
y = 12e^(-20/9000)
y ≈ 11.8767 kg (rounded to one decimal place)
Learn more about equation here:
https://brainly.com/question/29538993
#SPJ11
Suppose you travel 55 mi/h. How many hours would it take you to go 275 mi?
Answers
Answer:
5 hours
Step-by-step explanation:
275 mi/(55mi/h)=5h
or to put it simply 275/55=5
in the diagram PQRS is a circle centre O. If angel POQ = 150° angle QSR= 40° and angel SQP= 45° calculate angel RQS.
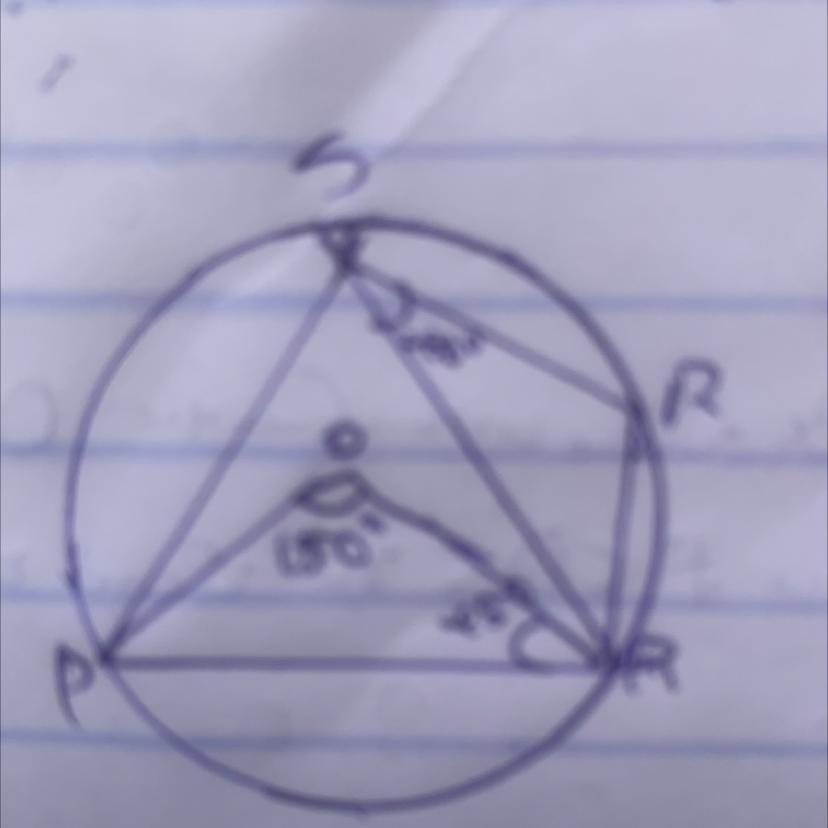
Answers
Answer:
the angle would be 40 degrees
Step-by-step explanation:
using the alternative angle property the angle is 40
Which of the following is the correct point-slope equation for the line that
passes through the point (-4,-2) and is parallel to the line given by
y = 5x + 44?
Ay+2= 5(x+4)
OB. y-4-5(x-2)
OC. y+4= 5(x+2)
OD. y-2= 5(x-4)
Answers
The correct point-slope equation for the line that passes through the point (-4,-2) and is parallel to the line given by y = 5x + 44 is: A. y + 2 = 5(x + 4)
How to determine an equation of this line?In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical expression:
y - y₁ = m(x - x₁)
Where:
x and y represent the data points.m represent the slope.Since the line is parallel to y = 5x + 44, the slope is equal to 5.
At data point (-4, -2) and a slope of 5, a linear equation for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - (-2) = 5(x - (-4))
y + 2 = 5(x + 4)
Read more on point-slope here: brainly.com/question/24907633
#SPJ1
A Jésica le piden hacer dos esculturas triangulares idénticas. En la primera le solicitan que su perímetro sea de 80 centímetros mientras que en la segunda requiere que sus lados midan x+4 , 3x+2 , y , 2x-2 ¿ que dimensiones tendrá la esculturas triangulares ?
me podrían ayudar ☹️ porfavor
Answers
La esculturas triangulares tendrán las siguientes medidas 16.66 cm, 40 cm y 23.32 cm.
¿Qué e el perímetro?Es la suma total de los lados del triángulo, en este caso el perímetro total es de 80.
¿Cómo calcular las dimensiones del triángulo?Se pueden calcular usando el total y la información sobre cada lado:
x+4 + 3x+2 + 2x-2 = 806x + 4 = 806x = 80 - 46x = 76x = 76/ 6x = 12.66Finalmente calcule cada lado:
A. x+4 = 12.66 + 4 = 16.66B. 3x + 2 = 3 x 12.66 + 2 = 39.98 o 40C. 2x - 2 = 23.32Aprenda más sobre perímetro en: https://brainly.com/question/24514946
1) Simplify each algebraic expression.
a) (10x+2) + (3x+5)

Answers
Answer:
13x + 7
Step-by-step explanation:
Given expression,
→ (10x + 2) + (3x + 5)
Now we have to,
→ Simplify the given expression.
Let's simplify the expression,
→ (10x + 2) + (3x + 5)
→ 10x + 2 + 3x + 5
→ (10x + 3x) + (2 + 5)
→ (13x) + (7)
→ 13x + 7
Hence, the answer is 13x + 7.
Which of the following statements are true for all sets of A,B, and C?
a.(A – C) ∩ (A – B) = A – (B ∪ C)
b.If A ∩ B = ∅, then A ⊂ B
c.∅ X A = ∅
d.(A – B) ∪ (B – C) = A – C
e.∅ ∩ {∅} = ∅
f.B X A = A X B
Answers
Aftre solving, the all option is false except option c. Only option c, ∅×A=∅ is correct because cartesian product with non empty set with empty set alsways gives empty set.
In the givn question we have to find which statement is true.
To solve the question we let;
A={1,2,3}; B={2,3,4}; C={2,3}
(a) The first option is (A – C) ∩ (A – B) = A – (B ∪ C)
Now solving the both side by putting the value
({1,2,3} – {2,3}) ∩ ({1,2,3} – {2,3,4}) = {1,2,3} – ({2,3,4} ∪ {2,3})
{1} ∩ {1,4} = {1,2,3} – {2,3,4}
{1} = {1,4} (False)
(b) If A ∩ B = ∅, then A ⊂ B
As we know that if If A ∩ B = ∅, then A=∅ and B=∅. That means both A and B will be empty set. So the option B is false.
(c) ∅ X A = ∅
As we know that cartesian product with non empty set with empty set alsways gives empty set. SO the option C is correct.
(d) (A – B) ∪ (B – C) = A – C
Now solving the both side by putting the value
({1,2,3} – {2,3,4}) ∪ ({2,3,4} – {2,3}) = {1,2,3} – {2,3}
{1,4} ∪ {4} = {1}
{1,4} = {1} (False)
(e) ∅ ∩ {∅} = ∅ (False)
(f) B X A = A X B (False)
To learn more about sets link is here
brainly.com/question/18877138
#SPJ4
true equilibrium constants are not expressed in terms of concentrations but rather in terms of
Answers
Answer:
the products and the reactants.
Step-by-step explanation:
Thats how true constants at equilibrium are expressed.
:) hope that helped . have a great day !
the symbol μ ˆ p represents the proportion of a sample of size n, not the proportion of a sample of size n. true or false
Answers
The statement ''the symbol μ ˆ p represents the proportion of a sample of size n, not the proportion of a sample of size n.'' is false because the symbol "μ ˆ p" does not represent the proportion of a sample of size n.
In statistical notation, the symbol "μ ˆ p" typically represents the sample proportion, which is an estimate of the population proportion. The sample proportion is obtained by dividing the number of occurrences of a specific event in the sample by the sample size.
On the other hand, the population proportion, denoted by "p," represents the proportion of the entire population that exhibits a certain characteristic or has a specific attribute.
The symbol "μ ˆ p" could be a typographical error or a confusion between different symbols used in statistics. The correct symbol to represent the sample proportion is usually denoted as "p ˆ" or "p-hat." The symbol "μ" typically represents the population mean.
Therefore, it is incorrect to state that "μ ˆ p" represents the proportion of a sample of size n.
To know more about statistical notation refer here:
https://brainly.com/question/28171663#
#SPJ11
Malika models the volume of a popcorn box as a right rectangular prism and the box
can hold 35 cubic inches of popcorn when it is full. Its length is 2 in and its width is
2% in. Find the height of the popcorn box in inches. Round your answer to the
nearest tenth if necessary.
Answers
The height of the popcorn box is 8.75 inches.
What is the rectangular prism?
A rectangular prism is a three-dimensional geometric shape with six rectangular faces. It is also known as a rectangular cuboid, or simply a cuboid. It has three dimensions: length, width, and height. It can be represented by the formula: V = lwh where l is the length, w is the width, and h is the height.
We can use the formula for the volume of a rectangular prism to solve this problem. The formula is:
V = l * w * h
where V is the volume, l is the length, w is the width, and h is the height. We know that the volume of the box is 35 cubic inches and that the length and width are 2 inches each. So we can substitute those values into the formula and solve for h:
35 = 2 * 2 * h
To find h, we'll divide both sides of the equation by 4.
h = 35/4 = 8.75
Hence, the height of the popcorn box is 8.75 inches.
To learn more about the rectangular prism, visit:
https://brainly.com/question/24284033
#SPJ1
If (fg)(x) = h(x) such that h of x is equal to the square root of the quantity 8 times x plus 6 end quantity which of the following could accurately represent f and g?
f of x is equal to the square root of the quantity 4 times x plus 3 end quantity and g of x is equal to the square root of the quantity 4 times x plus 3 end quantity
f of x is equal to the square root of the quantity 4 times x plus 3 end quantity and g of x is equal to the square root of 2
f (x) = 8x + 6 and g of x is equal to the square root of x
f of x is equal to the square root of x and g(x) = 8x + 6
Answers
The possible definitions of f(x) and g(x), considering the composition of the functions, are given as follows:
\(f(x) = \sqrt{x}\)g(x) = 8x + 6.What is the composite function of f(x) and g(x)?The composite function of f(x) and g(x) is given by the following rule:
(f ∘ g)(x) = f(g(x)).
It means that the output of the inside function serves as the input for the outside function.
The functions for this problem are defined as follows:
\(f(x) = \sqrt{x}\)g(x) = 8x + 6.As the composition of the functions is then given as follows:
\(h(x) = f(g(x)) = f(8x + 6) = \sqrt{8x + 6}\)
More can be learned about the composition of functions at https://brainly.com/question/10687170
#SPJ1
Describe a normally distributed phenomena using standard nomenclature.
Answers
In standard nomenclature, a normally distributed dataset is represented as \(N(µ, σ^2)\), where µ is the mean and \(σ^2\)is the variance (square of the standard deviation).
A normally distributed phenomenon using standard nomenclature can be described as follows:
A dataset is said to be normally distributed if it follows a bell-shaped curve, which is symmetrical around the mean (µ) and characterized by its standard deviation (σ). In standard nomenclature, a normally distributed dataset is represented as \(N(µ, σ^2)\), where µ is the mean and \(σ^2\)is the variance (square of the standard deviation).
For example, if we consider the heights of adult males in a large population, we may observe that the distribution is normally distributed with a mean height (µ) of 175 cm and a standard deviation (σ) of 10 cm. In this case, the nomenclature for this normally distributed phenomenon would be N(175, 100), as the variance is \(10^2 = 100\).
Learn more about nomenclature here:
https://brainly.com/question/13717281
#SPJ11
Given that sin(90 -5thetha) = Cos(180 - 0),
Find the value of theta
Answers
Answer:
θ = 54 - π/10 - (2 π n_1)/5 for n_1 element Z
or θ = -18 - π/10 - (2 π n_2)/5 for n_2 element Z
Step-by-step explanation:
Solve for θ:
sin(90 - 5 θ) = cos(180)
Hint: | Express the right hand side in terms of sine.
Rewrite the right hand side using cos(θ) = sin(θ + π/2):
sin(90 - 5 θ) = sin(π/2 + 180)
Hint: | Eliminate the sine from the left hand side.
Take the inverse sine of both sides:
90 - 5 θ = -180 + π/2 + 2 π n_1 for n_1 element Z
or 90 - 5 θ = 180 + π/2 + 2 π n_2 for n_2 element Z
Hint: | Look at the first equation: Isolate terms with θ to the left hand side.
Subtract 90 from both sides:
-5 θ = -270 + π/2 + 2 π n_1 for n_1 element Z
or 90 - 5 θ = 180 + π/2 + 2 π n_2 for n_2 element Z
Hint: | Solve for θ.
Divide both sides by -5:
θ = 54 - π/10 - (2 π n_1)/5 for n_1 element Z
or 90 - 5 θ = 180 + π/2 + 2 π n_2 for n_2 element Z
Hint: | Look at the second equation: Isolate terms with θ to the left hand side.
Subtract 90 from both sides:
θ = 54 - π/10 - (2 π n_1)/5 for n_1 element Z
or -5 θ = 90 + π/2 + 2 π n_2 for n_2 element Z
Hint: | Solve for θ.
Divide both sides by -5:
Answer: θ = 54 - π/10 - (2 π n_1)/5 for n_1 element Z
or θ = -18 - π/10 - (2 π n_2)/5 for n_2 element Z
what is the repeated-measures t statistic for a two-tailed test using the following scores? i ii 3 7 2 6 8 6 7 5 a. –1.732 b. –0.577 c. 0.577 d. 1.732
Answers
There is no repeated-measures t statistic for this two-tailed test using the given scores.
The repeated-measures t statistic for a two-tailed test can be calculated using the following formula:
t = (mean difference - hypothesized mean difference) / (standard deviation of the mean difference / square root of sample size)
To calculate the mean difference, subtract the first set of scores (i) from the second set of scores (ii) for each pair:
(3 - 7) = -4
(2 - 6) = -4
(8 - 6) = 2
(7 - 5) = 2
The mean difference is the sum of these differences divided by the sample size:
(-4 + -4 + 2 + 2) / 4 = -4 / 4 = -1
To calculate the standard deviation of the mean difference, first calculate the squared differences between the mean difference and each individual mean difference:
(-1 - (-1))^2 = 0
(-1 - (-1))^2 = 0
(-1 - (-1))^2 = 0
(-1 - (-1))^2 = 0
Then, calculate the sum of these squared differences and divide by the sample size minus 1:
(0 + 0 + 0 + 0) / (4 - 1) = 0 / 3 = 0
Finally, calculate the square root of the result:
sqrt(0) = 0
Now, substitute these values into the formula:
t = (-1 - 0) / (0 / sqrt(4)) = -1 / (0 / 2) = -1 / 0 = undefined
Since the standard deviation of the mean difference is 0, the denominator becomes 0 and the t statistic is undefined.
Therefore, there is no repeated-measures t statistic for this two-tailed test using the given scores.
Learn more about two-tailed test
brainly.com/question/8170655
#SPJ11
What percent of 65 is 13
Answers
Answer:
20 percent
Step-by-step explanation:
Just divide 100 by 65 and multiply that number by 13.
Answer:
20%
Step-by-step explanation:
This is the answer because:
1) Convert the fraction to a decimal, then multiply by 100:
13 x 100 ÷ 65 = 20
Therefore, the answer is 20%
Hope this helps! :D
You're playing a game where you defend your village from an orc invasion. There are 3 characters (elf, hobbit, or human) and 555 defense tools (magic, sword, shield, slingshot, or umbrella) to pick from.
If you randomly choose your character and tool, what is the probability that you won't be a hobbit or use an umbrella?
Answers
Answer:
There is a 1/3 chance of getting a hobbit, and a 0.1/11 chance of getting an umbrella.
A tent guy line supports one of the upright tent poles. It runs from the top of the pole to a peg in the ground two and a half metres away from the base of the pole. If the guy line is 359cm long, how tall is the upright tent pole? Give your answer in centimetres correct to the nearest centimetre.
Answers
Answer:
258 cm
Step-by-step explanation:
Given:
Distance from the base of the pole to the base of a tent guy line is \(2\frac{1}{2}\)
Length of a tent guy line is 359 cm
To find: Height of the upright tent pole
Solution:
Let AB denotes the pole and AC denotes a tent guy line.
According to Pythagoras theorem, in a right angled triangle, square of hypotenuse is equal to sum of squares of other two sides.
\(AC^2=AB^2+BC^2\)
\(AC=359 cm\\AB=x\\BC=2\frac{1}{2}\,m=\frac{5}{2}\,m=\frac{5}{2}\times 100=250\,cm\)
Therefore,
\((359)^2=x^2+(250)^2\\128881=x^2+62500\\128881-62500=x^2\\66381=x^2\\x=257.6\,cm\approx 258\,cm\)
Record the mass of the object based on the reading from the mass of the object is
the triple-beam balance
grams
Answers
Answer:
167
Step-by-step explanation:
Answer:
167
Step-by-step explanation:
In a random sample, 328 out of 920 12th graders in California smoked marijuana within the last year Answer questions 1-4, and round to 3 decimal places 1. Calculate the point estimate a. 0.391 b. 0.446 c. 0.524 d. 0.357
Answers
To calculate the point estimate, we divide the number of individuals in the sample who smoked marijuana within the last year (328) by the total number of individuals in the sample (920).
Point Estimate = Number of individuals who smoked marijuana / Total number of individuals in the sample
Point Estimate = 328 / 920 ≈ 0.357
Therefore, the point estimate is approximately 0.357.
The correct answer is d. 0.357.
Learn more about Point Estimate here: brainly.com/question/30888009
#SPJ11
t-tests, F test for homogeneity of variance, ANOVAS are all examples of ________________. a. Parametric, descriptive statistics.
b. Nonparametric, descriptive statistics
c. Parametric, inferential statistics.
d. Nonparametric, inferential statistics
Answers
T-tests, F test for homogeneity of variance, and ANOVAs are all examples of parametric, inferential statistics.
So, the correct answer is C.
Parametric statistics assumes that the data being analyzed follows a normal distribution and that the samples being compared have equal variances.
T-tests are used to compare means between two groups, while ANOVAs are used to compare means across three or more groups.
The F test for homogeneity of variance is used to test if the variances between two or more groups are equal.
These tests are inferential statistics because they allow researchers to make inferences about a larger population based on a sample of data.
Hence, the answer of the question is C.
Learn more about ANOVA at https://brainly.com/question/30127764
#SPJ11
What is a formula for the nth term of the given sequence? 24 , 36 , 54
Answers
The formula for the nth term of the series will be (11+n)*(n+1).
What is series?A series in mathematics is essentially the process of adding an infinite number of quantities, one after the other, to a specified starting quantity. A significant component of calculus and its extension, mathematical analysis, is the study of series. The fundamental concepts in mathematics are series and sequence. A series is the total of all elements, whereas a sequence is an ordered group of elements in which repeats of any kind are permitted. One of the typical instances of a series or a sequence is an arithmetic progression.
In this the pattern of the series is
24=12*2
39=13*3
54=14*4
hence The formula for the nth term of the series will be (11+n)*(n+1).
To know more about series, visit
https://brainly.com/question/15415793
#SPJ1
Solving Equations with Variables on Both Sides

Answers
Answer: x=-9
Step-by-step explanation: First, combine like terms. 3x+4-2x=-5
Then x+4 = -5
x=-9
Find the vectors t, n, and b at the given point. r(t) = 3 cos t, 3 sin t, 3 ln cos t , (3, 0, 0)
Answers
Here are the vectors **t**, **n**, and **b** at the given point:
* **t** = (-3 sin t, 3 cos t, 0)
* **n** = (-3 cos t, -3 sin t, 3 / cos^2 t)
* **b** = (3 cos^2 t, -3 sin^2 t, -3)
The vector **t** is the unit tangent vector, which points in the direction of the curve at the given point. The vector **n** is the unit normal vector, which points in the direction perpendicular to the curve at the given point. The vector **b** is the binormal vector, which points in the direction that is perpendicular to both **t** and **n**.
To find the vectors **t**, **n**, and **b**, we can use the following formulas:
```
t(t) = r'(t) / |r'(t)|
n(t) = (t(t) x r(t)) / |t(t) x r(t)|
b(t) = t(t) x n(t)
```
In this case, we have:
```
r(t) = (3 cos t, 3 sin t, 3 ln cos t)
r'(t) = (-3 sin t, 3 cos t, 3 / cos^2 t)
```
Substituting these into the formulas above, we can find the vectors **t**, **n**, and **b** as shown.
The vectors **t**, **n**, and **b** are all orthogonal to each other at the given point. This is because the curve is a smooth curve, and the vectors are defined in such a way that they are always orthogonal to each other.
to learn more about perpendicular click here:
brainly.com/question/29368768
#SPJ11
The binormal vector (b) is perpendicular to both the tangent and normal vectors and completes the orthogonal coordinate system.
To find the vectors t, n, and b at the given point, we need to calculate the first derivative, second derivative, and third derivative of the position vector r(t).
Given r(t) = (3 cos t, 3 sin t, 3 ln cos t), we can calculate the derivatives as follows:
First derivative:
r'(t) = (-3 sin t, 3 cos t, -3 sin t / cos t)
Second derivative:
r''(t) = (-3 cos t, -3 sin t, -3 cos t / cos^2 t + 3 sin^2 t / cos t)
= (-3 cos t, -3 sin t, -3 cos t / cos^2 t + 3 tan^2 t)
Third derivative:
r'''(t) = (3 sin t, -3 cos t, 6 cos t / cos^3 t - 6 sin t / cos t)
= (3 sin t, -3 cos t, 6 sec^3 t - 6 tan t sec t)
At the given point (3, 0, 0), substitute t = 0 into the derivatives to find the vectors:
r'(0) = (0, 3, 0)
r''(0) = (-3, 0, 3)
r'''(0) = (0, -3, 6)
Therefore, at the given point, the vectors t, n, and b are:
t = r'(0) = (0, 3, 0)
n = r''(0) = (-3, 0, 3)
b = r'''(0) = (0, -3, 6)
These vectors represent the tangent, normal, and binormal vectors, respectively, at the given point.
The tangent vector (t) represents the direction of motion of the curve at that point. The normal vector (n) is perpendicular to the tangent vector and points towards the center of curvature.
The binormal vector (b) is perpendicular to both the tangent and normal vectors and completes the orthogonal coordinate system.
Remember to check your calculations and units when applying this method to different functions.
To know more about derivatives visit:
https://brainly.com/question/25324584
#SPJ11
It takes your equipment 3 minutes to travel 264 feet. what speed is the equipment traveling?
Answers
Answer:
To determine the speed, we can use the formula:
speed = distance / time
where distance is measured in feet and time is measured in minutes.
In this case, the distance is 264 feet and the time is 3 minutes. Plugging these values into the formula, we get:
speed = 264 feet / 3 minutes
simplifying, we get:
speed = 88 feet/minute
Therefore, the equipment is traveling at a speed of 88 feet per minute.
What is the percent of change from 46 to 69?
Answers
Answer:
A change from 46 to 69 represents a positive change (increase) of 50% Use the formula found below on this webpage to find the percent change by replacing the given values: Percent change = New - Old |Old| × 100% Percent change = 69 - 46 |46| × 100% =
Step-by-step explanation:
Used my brain (Lol brain)
I hope it’s help
.In a multiple regression model, the variance of the error term `eâ is assumed to be the same for all values of the dependent variable.
A)the same for all values of the independent variable
B)zero.
C)the same for all values of the independent variable.
D)one.
Answers
In a multiple regression model, the variance of the error term e is assumed to be the same for all values of the independent variable. Therefore, the correct option is C) the same for all values of the independent variable.
In multiple regression, we use several independent variables to predict the values of the dependent variable. The model estimates the relationship between the independent variables and the dependent variable by calculating the coefficients of the independent variables.
The error term e represents the difference between the predicted value of the dependent variable and the actual value of the dependent variable.
The assumption of constant variance of the error term e is known as homoscedasticity. It means that the variance of the errors is the same for all levels of the independent variables.
This assumption is important because, if the errors have different variances across the levels of the independent variable, the model may not accurately capture the relationship between the independent variables and the dependent variable, leading to biased and unreliable results. so, the correct answer is C).
To know more about regression model:
https://brainly.com/question/31969332
#SPJ4
determine if the equation is a linear equation -x + 3y^2=18
Answers
Answer:
No
Step-by-step explanation:
Linear equations must have no squares, roots, cubes, or any powers. If the graph has an asymptote or any restrictions, it is not a linear function.
A linear function will only appear in either point-slope form or slope-intercept form. These forms will not have square roots or powers in them.
-x + 3y² = 18
We know here that this is not a linear function. But we can try to write it in slope-intercept form:
3y² = x + 18
y² = x/3 + 6
y = √(x/3 + 6)
We can see from here that our graph is a square root function and has a restricted domain (no negative numbers).
Alternatively, we can graph the equation to see if it is a constant line (linear equation) or not. When we do so, we see that it is definitely not a linear function:

Find the sum of 102 + (-97) + 3 =
Answers
Answer:
8
Step-by-step explanation:
You can solve this a few different ways.
Firstly I did 102 - 97 = 5
Then I took 5 and added 3 to it
5 + 3 ---> which gets us 8 as our final answer.
Hope I helped!
Have a great day!
which table shows a proportional relationship. i meed help

Answers
Explain why player I has a winning strategy in problem 1 above when E={x:x >1/2}.What is player I’s winning strategy when E={x:x≥2/3}? What is player II’s winning strategy when E={x:x >2/3}?
Answers
When E={x:x>1/2}, player I has a winning strategy since they can choose a number greater than 1/2 and player II will never be able to choose a number greater than the one chosen by player I.
This is because player II's choices are limited to numbers between 0 and 1, while player I's choices are not limited and they can choose any number greater than 1/2. When E={x:x≥2/3}, player I's winning strategy is to choose a number greater than or equal to 2/3.
This ensures that player II cannot choose a number greater than the one chosen by player I, as player II's choices are still limited to numbers between 0 and 1. Player II's winning strategy when E={x:x>2/3} is to choose a number as close as possible to 2/3, such as 5/8 or 7/10, without going over 2/3. This will allow them to be as close to the number chosen by player I as possible while still staying within the limits of the set.
know more about winning strategy here
https://brainly.com/question/3222488#
#SPJ11