find a 2×2 matrix such that [−4−2] and [−54] are eigenvectors of the matrix with eigenvalues 4 and −10, respectively. [
Answers
The 2x2 matrix with eigenvectors [-4,-2] and [-5,4], and eigenvalues 4 and -10 respectively, is A= \(\left[\begin{array}{ccc}-2&-2\\5/2&-3/2\\\end{array}\right]\)
Let A be the 2x2 matrix we want to find, and let v₁ = [-4, -2] and v₂ = [-5, 4] be the given eigenvectors corresponding to eigenvalues 4 and -10, respectively. Then, by definition of eigenvectors, we have
Av₁ = 4v₁
Av₂ = -10v₂
Writing this out
\(\left[\begin{array}{ccc}a11&a12\\a21&a22\\\end{array}\right]\) * \(\left[\begin{array}{ccc}4\\2\end{array}\right]\) = 4 *\(\left[\begin{array}{ccc}-4\\-2\\\end{array}\right]\)
and
\(\left[\begin{array}{ccc}a11&a12\\a21&a22\\\end{array}\right]\) *\(\left[\begin{array}{ccc}5\\4\end{array}\right]\) = -10* \(\left[\begin{array}{ccc}-5\\4\\\end{array}\right]\)
Expanding these equations, we get the following system of linear equations
-4a₁₁ - 2a₁₂ = -16
-4a₂₁ - 2a₂₂ = -8
-5a₁₁ + 4a₁₂ = 50
-5a₂₁ + 4a₂₂ = -40
Solving this system of equations, we get
a₁₁ = -2, a₁₂ = -2
a₂₁ = 5/2, a₂₂ = -3/2
Therefore, the matrix we are looking for is
A = \(\left[\begin{array}{ccc}-2&-2\\5/2&-3/2\\\end{array}\right]\)
To know more about matrix:
https://brainly.com/question/28180105
#SPJ4
Related Questions
A friend of yours, a senior, took the Graduate Record Exam in September and scored in the 99th percentile. In February, your friend took the same exam over again. This time your friend scored in the 90th percentile. As a research methods student, you told your friend that his/her lowered score was most likely due to:
Answers
His/her lowered score was most likely due to statistical regression.
How to determine the reason?The missing options in the question are:
A. compensation rivalry B. Demoralization C. Differential selection
D. Testing E. Statistical regression
From the question, we have:
September = 99th percentileFebruary = 90th percentileA change (whether higher or lower) in the score is caused by statistical regression.
This is so because several variables could attribute to the change in the score.
The relationship between these variables is referred to as statistical regression
Read more about statistical regression at:
https://brainly.com/question/25987747
#SPJ12
Help with question in photo?

Answers
let's recall that two tangent lines to the same circle meeting outside it, will have the same length, so all those pair of tangent lines are equal in length.
Check the picture below.

Which statement is not always true for a parallelogram?
A. Consecutive angles are supplementary.
B. Diagonals are congruent.
C. Opposite sides are congruent.
D. Opposite angles are congruent.
Answers
Explanation:
If the diagonals are congruent, then we'd have a rectangle. Any rectangle is a parallelogram, but not the other way around.
If we had a non-rectangular parallelogram, with none of the angles 90 degrees, then the diagonals will not be the same length.
Choices A, C and D are true for any parallelogram (rectangle or not).
the number which best completes the sequence below is:
10 30 15 16 48 24 25
a) 45 b)75 c)72 d)47 e)70
Answers
The number which best completes the sequence is option c) 72.
The sequence seems to be alternating between multiplying by 3 and dividing by 2.
Starting with 10, we have:
10 x 3 = 30
30 ÷ 2 = 15
15 + 1 = 16
16 x 3 = 48
48 ÷ 2 = 24
24 + 1 = 25
So, the next number in the sequence should be:
25 x 3 = 75
75 ÷ 2 = 37.5
However, none of the answer options match 37.5. Therefore, we need to look for a pattern that matches one of the answer options.
If we multiply 25 by 3 and then divide by 2, we get 37.5. However, if we continue with this pattern, we get:
37.5 x 3 = 112.5
112.5 ÷ 2 = 56.25
Again, none of the answer options match 56.25.
Let's try multiplying 24 by 3 and then dividing by 2:
24 x 3 = 72
72 ÷ 2 = 36
Since 36 is not in the sequence, we can eliminate option b) 75.
Therefore, the number which best completes the sequence is option c) 72.
The number which best completes the sequence 10, 30, 15, 16, 48, 24, 25 is:
c) 72
The sequence can be described as alternating between multiplying by 3 and dividing by 2, then adding 1.
10 x 3 = 30
30 / 2 = 15
15 + 1 = 16
16 x 3 = 48
48 / 2 = 24
24 + 1 = 25
25 x 3 = 75
To know more about Sequence click here.
brainly.com/question/30262438
#SPJ11
To make layla's favorite shade of purple, she needs 8 ounces of blue for every 14 ounces of red. how many ounces of blue would she need for 63 ounces of red?
Answers
To make layla's favorite shade of purple, she needs 8 ounces of blue for every 14 ounces of red, and she need for 63 ounces of red, then the blue would be 36 ounces.
To make layla's favorite shade of purple, she needs 8 ounces of blue for every 14 ounces of red.
Based on the given conditions,
She needs ounces of blue = 8
For every ounces of red = 14
She need for 63 ounces of red = 63
Let us assume,
She need for ounces of blue = x
So,
We can write,
Need for 63 ounces of red ⇒ Every 14 ounces of red
she needs 8 ounces of blue ⇒ She need for X ounces of blue
Then,
\(\frac{8}{14}\) = \(\frac{x}{63}\)
We can solve the equation of \(\frac{8}{14}\) = \(\frac{x}{63}\)
Swap the sides,
\(\frac{x}{63}\) = \(\frac{8}{14}\)
Divide both sides of the equation by the coefficient of variable,
\(x\) = \(\frac{8}{14} *63\)
Simplify fractions,
x = 4*9
Calculate the product or quotient,
x = 36
Therefore,
To make layla's favorite shade of purple, she needs 8 ounces of blue for every 14 ounces of red, and she need for 63 ounces of red, then the blue would be 36 ounces.
To learn more about information visit Arithmetic problems :
brainly.com/question/28675891
#SPJ4
In Exercises 1-12, use the law of sines to approximate the required part(s) of triangle ABC. Give both solutions if more than one triangle satisfies the given conditions. Problem 2: If α=74 ∘
,γ=36 ∘
, and c=6.8, find a. Problem 4: If α=46 ∘
,β=88 ∘
, and c=10.5, find b. Problem 6: If β=16 ∘
30 ′
,γ=84 ∘
40 ′
, and a=15, find c.
Answers
Problem 2: Using the law of sines with α=74°, γ=36°, and c=6.8, we find that a≈10.67. Problem 4: With α=46°, β=88°, and c=10.5, b≈6.77. Problem 6: Given β=16°30', γ=84°40', and a=15, c≈4.27.
Problem 2:
Using the law of sines, we can set up the following equation:
sin(α) / a = sin(γ) / c
Plugging in the given values, we have:
sin(74°) / a = sin(36°) / 6.8
Now we can solve for a:
a = (sin(74°) / sin(36°)) * 6.8
a ≈ 10.67
Problem 4:
Using the law of sines, we can set up the following equation:
sin(α) / a = sin(β) / b
Plugging in the given values, we have:
sin(46°) / a = sin(88°) / 10.5
Now we can solve for b:
b = (sin(46°) / sin(88°)) * 10.5
b ≈ 6.77
Problem 6:
Using the law of sines, we can set up the following equation:
sin(β) / b = sin(γ) / c
Plugging in the given values, we have:
sin(16°30') / b = sin(84°40') / 15
Now we can solve for c:
c = (sin(16°30') / sin(84°40')) * 15
c ≈ 4.27
In all the problems, we used the law of sines to relate the angles and sides of the triangle, and then solved for the required side lengths using the given values and trigonometric ratios.
To learn more about angles click here
brainly.com/question/13954458
#SPJ11
what is 3 5/9 minus 2 1/3
Answers
Answer:
11/9 or 1 2/9
Step-by-step explanation:
3 5/9=32/9
2 1/3=7/3
LCM is 9
7/3=21/9
32/9-21/9
=11/9
=1 2/9
Solve -2/3-x > 8 or -2/3-x < 4
Answers
Answer:
x=<_26/3
OR
x=>_14/3
Add them together and divide
four people (john, paul, george, and ringo) are seated in a row on a bench. the number of ways to order the four people so that john is next to paul is 12. how many ways are there to order the four people on the bench so that john is not next to paul?
Answers
The Number of ways that four people can be seated on the bench so that john is not next to paul is 12
Permutations :
In mathematics, An arrangement of things or items in a specific sequence is known as a permutation. One should think about both the selection and the arrangement while dealing with permutation. In permutations, ordering is crucially important.
The arrangement of n items in r ways is given by
ⁿPr = n! /(n-r)!Here we have
4 people (John, Paul, George, and Ringo) are seated in a row on a bench
Here total No of ways that 4 can be seated = 4 × 3 × 2 × 1 = 24
The number of ways of seating the four people so that john is next to paul is 12
Then the number of ways the four people on the bench so that john is not next to paul can find as given below
= Total No of ways, 4 can be seated - No of ways that john next to paul
= 24 - 12 = 12
Learn more about Permutations at
https://brainly.com/question/27058178
#SPJ1
a college dean would like to estimate a population mean to within 40 units with 99% confidence given that the population standard deviation is 200. a. what sample size should be used? b. what sample size should be used if the standard deviation is changed to 50? c. what sample size should be used if using a 95% confidence level? d. what sample size should be used if we wish to estimate the population mean to within 10 units?
Answers
Sample size required is 333, 42, 97 and 33,285, respectively using confidence level and different parameters of standard deviation.
To estimate a population mean to within 40 units with 99% confidence and a population standard deviation of 200, the sample size required can be calculated using the formula
n = (Zα/2)² * (σ²) / (E²)
where Zα/2 is the z-score corresponding to the desired level of confidence (99% in this case), σ is the population standard deviation, and E is the desired margin of error (40 units).
Plugging in the values, we get
n = (2.576)² * (200)²/ (40)²
n = 332.84
Therefore, a sample size of at least 333 should be used.
If the population standard deviation is changed to 50, the same formula can be used with the new value of σ:
n = (2.576)² * (50)²/ (40)²
n = 41.68
Therefore, a sample size of at least 42 should be used.
If using a 95% confidence level, the z-score changes to 1.96
n = (1.96)² * (200)²/ (40)²
n = 96.04
Therefore, a sample size of at least 97 should be used.
To estimate the population mean to within 10 units, the margin of error (E) is changed to 10 in the formula, and the sample size is recalculated
n = (2.576)² * (200)² / (10)²
n = 33,284
Therefore, a sample size of at least 33,285 should be used.
To know more about confidence interval:
https://brainly.com/question/29680703
#SPJ4
The required sample size should be 166 to estimate the population mean within 40 units with 99% confidence, given a population standard deviation of 200.
To determine the required sample size for estimating a population mean with a given level of confidence and margin of error, we can use the formula:
n = (Z * σ / E)^2
Where:
n = Sample size
Z = Z-score corresponding to the desired confidence level (in this case, 99% confidence corresponds to a Z-score of 2.576)
σ = Population standard deviation
E = Margin of error (in this case, 40 units)
Substituting the given values into the formula, we have:
n = (2.576 * 200 / 40)^2
Simplifying further:
n = (12.88)^2
n ≈ 165.6544
Since the sample size must be a whole number, we round up the value to the nearest integer:
n = 166
Therefore, the required sample size should be 166 to estimate the population mean within 40 units with 99% confidence, given a population standard deviation of 200.
To know more about sample size refer here:
https://brainly.com/question/31734526#
#SPJ11
Really easy, Really need help!
Answers
Answer:
I don't see what the question is
how do i do this pls explain the steps
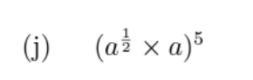
Answers
Answer:
\(a^{\frac{15}{2} }\)
Step-by-step explanation:
Using the rules of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
\((a^m)^{n}\) = \(a^{mn}\)
(\(a^{\frac{1}{2} }\) × a)^5
= \((a^{\frac{1}{2}+1) }\)^5
= \((a^{\frac{3}{2}) } ^{5}\)
= \(a^{\frac{15}{2} }\)
Help
Describe a pattern in each sequence. Then find the next two terms of the difference.
1, 5, 25, 125, …
Answers
1, 5, 25, 125
This is a geometric sequence since there is a common ratio between each term. In this case, multiplying the previous term in the sequence by
5 gives the next term. In other words, an=a1⋅rn−1. Geometric Sequence: r=5
This is the form of a geometric sequence.an=a1rn−1 Substitute in the values of a1=1 and r=5.an=(1)⋅(5)n−1 Multiply (5)n−1 by 1. an=5n−1
-8 5/9 = 4 2/3w
.............................
Answers
Answer:
w = -11/6
Step-by-step explanation:
-8 5/9 = 4 2/3w
-8 5/9 = -77/9
4 2/3 = 14/3
So, our equation is
-77/9 = 14/3w
Divided both sides by 14/3
w = -11/6
PLS HELP ASAP I NEED THIS

Answers
Answer:
D
Step-by-step explanation:
Firstly let's see definition of Rational numbers ,
Rational numbers :-
The number in the form of p/ q where p and q are integers and q is not equal to zero is called a Rational number .From the options , look at option D ,its
→ √400
→ √{20²}
→ 20
Hence option D is correct.the radius of a sphere is increasing at a rate of 2 mm/s . how fast is the volume increasing when the diameter is 60 mm ?
Answers
When the diameter of the sphere is 60 mm, its radius is 30 mm. The formula for the volume of a sphere is V = (4/3)πr^3, where r is the radius.
To find how fast the volume is increasing, we need to take the derivative of V with respect to time, which gives dV/dt = 4πr^2 (dr/dt). Substituting the given values, we get dV/dt = 4π(30)^2 (2) = 7200π mm^3/s. Therefore, the volume of the sphere is increasing at a rate of 7200π mm^3/s when the diameter is 60 mm. The radius of a sphere is increasing at a rate of 2 mm/s. When the diameter is 60 mm, the radius is 30 mm. The volume of a sphere is given by the formula V = (4/3)πr³. Using the chain rule, dV/dt = (4/3)π(3)r²(dr/dt), where dV/dt is the rate of volume increase and dr/dt is the rate of radius increase. Plugging in r = 30 mm and dr/dt = 2 mm/s, we get dV/dt = 4π(30)²(2) = 7200π mm³/s. So, the volume is increasing at a rate of 7200π mm³/s when the diameter is 60 mm.
To learn more about sphere, visit:
https://brainly.com/question/22124707
#SPJ11
Does the average Washington State University student drive more or less than 300 miles from Pullman to home? In a sample of 226 students, the sample mean mileage was 285 miles with a sample standard deviation of 50 miles. Plotting the data, we see that the sample is approximately normal. (a) (4 points) Determine if a one-sided or two-sided confidence interval is appropriate for this situation. Explain your reasoning. (b) (10 points) Compute a 95% confidence interval for. Write your solution in interval notation. Interpret the meaning of the interval in the context of the situation. (c) (4 points) Compared the the confidence interval calculated above, if the confidence level is decreased to 90%, the new confidence interval is If the confidence level is increased to 99%, the new confidence interval is __. A. wider, wider B. narrower, narrower C. wider, narrower D. narrower
Answers
A two-sided confidence interval is appropriate because the research question is about whether the average mileage is significantly different from 300 miles.
(a) To determine if a one-sided or two-sided confidence interval is appropriate for this situation, we need to consider the research question and the nature of the hypothesis being tested. If the research question is specifically focused on whether the average mileage is less than or greater than 300 miles, then a one-sided confidence interval would be appropriate. On the other hand, if the research question is broader and seeks to determine whether the average mileage is significantly different from 300 miles (i.e., it could be less or greater), then a two-sided confidence interval would be appropriate.
(b) To compute a 95% confidence interval, we can use the formula:
CI =X ± (Z * (σ/√n))
Where X is the sample mean, Z is the z-value corresponding to the desired confidence level (in this case, 95% corresponds to Z = 1.96 for a large enough sample), σ is the population standard deviation (unknown, so we use the sample standard deviation), and n is the sample size.
Plugging in the given values:
CI = 285 ± (1.96 * (50/√226))
Simplifying the expression:
CI = 285 ± (1.96 * 3.322)
CI = [278.15, 291.85]
Interpretation: The 95% confidence interval for the average mileage from Pullman to home is [278.15, 291.85]. This means that we are 95% confident that the true average mileage of all Washington State University students falls within this interval. It suggests that based on the sample data, the average mileage is likely to be between 278.15 and 291.85 miles.
(c) If the confidence level is decreased to 90%, the new confidence interval will be narrower since a smaller confidence level requires less certainty, resulting in a narrower interval. Conversely, if the confidence level is increased to 99%, the new confidence interval will be wider as a higher confidence level demands greater certainty, leading to a wider interval to capture a larger range of potential values. Therefore, the answer is D. narrower for a confidence level of 90% and A. wider for a confidence level of 99%.
Learn more about confidence level : brainly.com/question/22851322
#SPJ11
How to find missing angle on triangle with one angle.
Answers
Answer:
You look to see if one of the angles has a box around it and you add up the other angle with 90 and then subtract the whole thing by 180 because there are 180 degrees in a triangle.
Step-by-step explanation:
See above.
I need help with this

Answers
Answer:
draw another segment I think. __________
Step-by-step explanation:
The odds in favor of an event are 3 to 4. What is the probability of the event?
37
Answers
The probability from the odds is 3/7
How to determine the probability?The value of the odds is given as
Odds = 3 to 4
Represent the odds as a fraction
So, we have the following representation
Odds = 3/4
To convert the odds to probability, we make use of the following equation
Probability = Odds/(1 + Odds)
Substitute the known values in the above equation, so, we have the following representation
Probability = (3/4)/(3/4 + 1)
Evaluate the sum
Probability = (3/4)/(7/4)
Evaluate the quotient
Probability = 3/7
Hence, the probability is 3/7
Read more about odds and probability at
brainly.com/question/9760260
#SPJ1
Add or subtract rational numbers! - 12 + 6
Answers
Answer:
-6
Step-by-step explanation:when there is a negative you whuld do 6+-12
Definition of substance abuse
Answers
Answer: overindulgence in or dependence on an addictive substance, especially alcohol or drugs.
overindulgence in or dependence on an addictive substance, especially alcohol or drugs
Amille runs every morning before school. On Monday, she ran 2.36 miles. On Tuesday, she ran 4.88 miles. On Wednesday, she ran 3.19 miles. After she ran on Thursday, her total mileage for the week was 12.81 miles. How many miles did she run on Thursday?
Answers
Answer: Distance she ran on Thursday = 2.38 miles
Step-by-step explanation:
Given, Amille ran on Monday = 2.36 miles
On Tuesday, she ran 4.88 miles.
On Wednesday, she ran 3.19 miles.
Total distance she ran till Thursday = 12.81 miles.
Now, Distance she ran on Thursday = (Total distance) - (Distance ran on Monday to Wednesday)
= 12.81-(2.36+4.88+3.19)
= 12.81-10.43
= 2.38 miles
Hence, Distance she ran on Thursday = 2.38 miles
Answer the question below
Answers
B) 5
C) 2
Hope this works
The measure of the supplement of an angle is 60 less than three times the measure of the complement of the angle. Find the measure of the angle.
Answers
Answer:
The measure of the angle is 15 degree.
Step-by-step explanation:
The measure of the supplement of an angle is 60 less than three times the measure of the complement of the angle.
Supplementary angles are those that add up to 180, and complementary angles add up to 90.
Let \(x\) represent the angle.
\((180^{\circ} - x)\) is the supplementary angle and \((90^{\circ}-x)\) is the complementary angle.
\(180^{\circ}-x=3(90^{\circ}-x)-60^{\circ}\\180^{\circ}-x=270^{\circ}-3x-60^{\circ}\\180^{\circ}-x+3x=210^{\circ}\\2x=30^{\circ}\\x=15^{\circ}\)
\((90-15)^{\circ}=75^{\circ}\) is the complementary
\((180-15)^{\circ}=165^{\circ}\) is the supplementary angle
Can someone please help me?
A stack of 33 CDs is 1.5 inches high. How many CDs would be in a stack that is 3.5 inches high? Write a proportion to represent his situation.
Answers
Step by step:
Since we are writing a proportion it will look like this .....
33/1.5 = x/3.5 ( 33 over 1.5 and x over 3.5)
Now that we have our proportion , you cross multiply.....
33 x 3.5 = 115.5
“X” x 1.5 = 1.5x
So now you will have an equation that looks like this....... 1.5x=115.5
Once you have that then you divide 1.5 from each side , then after that then you should have x=77
So it takes 77 CD’s to be in a 3.5 inch high stack .
Hoped this helped , if it didn’t I apologize
Good luck
Let a,b, and c be real numbers such that 4a+2b+c=0 and ab>0. Then the equation ax 2 +bx+c=0 has
Answers
Since ab > 0, it is clear that the discriminant D > 0. Therefore, the equation ax^2 + bx + c = 0 has two distinct real roots.
Since 4a + 2b + c = 0, we can rewrite c as c = -4a - 2b. Substituting this into the quadratic equation ax^2 + bx + c = 0 gives ax^2 + bx - 4a - 2b = 0. Factoring out an 'a' gives a(x^2 + (b/a)x - 4) - 2b = 0.
Since ab > 0, we know that a and b must have the same sign. This means that either both a and b are positive or both a and b are negative. In either case, (b/a) is negative. So we can rewrite the equation as a(x^2 - |(b/a)|x - 4) - 2b = 0.
To solve for the roots of the equation, we can use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / 2a. Plugging in the coefficients, we get x = (-b ± √(b^2 - 4a(-4a-2b))) / 2a, which simplifies to x = (-b ± √(b^2 + 16ab)) / 2a.
Since ab > 0, we know that b^2 + 16ab > 0. Therefore, the quadratic equation ax^2 + bx + c = 0 has two real roots.
Based on the information provided, let's consider the equation ax^2 + bx + c = 0, where a, b, and c are real numbers and 4a + 2b + c = 0. Since ab > 0, both a and b have the same sign (either both positive or both negative).
The given equation can be rewritten as a quadratic equation in the standard form:
ax^2 + bx + c = 0
Using the discriminant formula, D = b^2 - 4ac, we can analyze the nature of the roots of the quadratic equation. Given that 4a + 2b + c = 0, we can express c as:
c = -4a - 2b
Now, let's plug this value of c into the discriminant formula:
D = b^2 - 4a(-4a - 2b)
D = b^2 + 16a^2 + 8ab
Since ab > 0, it is clear that the discriminant D > 0. Therefore, the equation ax^2 + bx + c = 0 has two distinct real roots.
Visit here to learn more about quadratic equation : https://brainly.com/question/30098550
#SPJ11
Use the figure to find the measure of the angle (#1-15)

Answers
Answer:
1. 82 2. 82 3. 82 4. 98 5. 123 6. 122 7. 119 8. 60 9. 60 10. 125 11. 35 12. 105
if you are going to receive $2,000 in six years from now, how much is that worth today, assuming 5 nnual simple interest? review later $1,538.46 $1,780.32 $1,904.76 $2,600.00
Answers
The initial amount is worth $ 1538.46
Simple interest:Simple interest is a type of interest that is calculated only on the principal amount of a loan or investment, without taking into account any additional interest that may be added over time.
Simple interest is calculated as a percentage of the principal amount and is usually expressed as an annual rate.
The formula to calculate simple interest is:
Simple Interest = Principal x Rate x Time/ 100
Here we have
You are going to receive $2,000 in 6 years from now
The annual simple interest rate is 5%
Let 'P' be the initial or principal amount
Using the formula, I = PTR/100
Simple interest will gain on 'P' at 5% for 6 years
=> I = P(6)(5)/100
=> I = 0.3P
And total amount = P + 0.3P = 1.3P
It is given that after 6 years we get $ 2000
=> 1.3P = 2000
=> P = 1538.46
Therefore,
The initial amount is worth $ 1538.46
Learn more about Simple interest at
https://brainly.com/question/28559489
#SPJ1
If F(x) = 2x +4, which of the following is the inverse of F(x)?
x4)
A. F'(x) = 7(x+4)
O B. F'(x) = 2(x+
C. F"(x) = 2(x == 4)
D. F'(x) = 7(x-4)