f
2x2 - 7x-4
Simplify
x2 - 5x +4
2x +1
x-1
2x + 1
x+1
2-7x
5x
DONE

Taking a difference, we can see that the trip to city C is 482.6 mi longer.

Here we know that the distance from city a to city b is 256.8 miles, and the distance from city a to city c is 739.4 miles

To find how much farther is the trip to city c than the trip to city b, we just need to take the difference between the two distances above.

That means that we need to take the distance to city c and subtract the distance to city b.

We will get:

739.4 mi -  256.8 mi = 482.6 mi

The trip to city C is 482.6 mi more than the trip to city B.

Learn more about differences at:

https://brainly.com/question/17695139

#SPJ1

Therefore, in about 15 years and 2 months, the senior class will have about 100 students.

An equation is a statement that expresses the equality of two mathematical expressions using mathematical symbols such as variables, numbers, and mathematical operations. The equality is represented by an equal sign "=" between the two expressions. Equations are used to represent mathematical relationships and solve problems in various fields such as physics, chemistry, engineering, and economics.

Given by the question.

Let P be the initial population of the senior class in the high school, and r be the rate of decrease in population per year (in decimal form).

Then, we can write the following equation to represent the situation:

P\((1-r)^{n}\) = 100

We know that the current population of the senior class is 320, so we can substitute these values into the equation:

320\((1-0.07)^{n}\) = 100

Simplifying the equation, we get:

\(0.93^{n}\) = 0.3125

Taking the natural logarithm of both sides, we get:

n ln (0.93) = ln (0.3125)

Dividing both sides by ln (0.93), we get:

n = ln (0.3125) / ln (0.93)

Using a calculator, we find that n is approximately equal to 15.21 years.

To learn more about logarithm:

https://brainly.com/question/12996775

#SPJ1

Answer:

C. (-1, 3)

Step-by-step explanation:

Label the 2 equations:

5y= 7x +22 -----(1)

x= -6y +17 -----(2)

Substitute (2) into (1):

5y= 7(-6y +17) +22

5y= -42y +119 +22 (Expand bracket)

5y= -42y +141 (Simplify)

42y +5y= 141 (+42y on both sides)

47y= 141

y= 141 ÷47 (÷47 on both sides)

y= 3

Substitute y= 3 into (2):

x= -6(3) +17

x= -18 +17

x= -1

Thus, the solution is (-1, 3).

The polar form of the complex number is expressed as r =  4√3 (cos (2π/3) ) +  i sin(2π/3).

option B.

The polar form of the complex number is expressed in terms of its magnitude and argument as follows;

The magnitude of the complex number is calculated as;

|r| = √((-2√3)²+ (-6)²)

|r| = √(12 + 36)

|r| = √48

|r| = 4√3

The argument is calculated as follows;

θ = arctan (-6 / (-2√3))

θ = arctan (3 / √3)

θ = arctan (√3)

θ = 60⁰ = π/3 = 2π/3

The polar form of the complex number is expressed as;

r =  4√3 (cos (2π/3) ) +  i sin(2π/3)

Learn  more about polar form here: https://brainly.com/question/28967624

#SPJ1

The event that none of the events E, F nor G occur is (E U F U G)'

Given,

Three events are E, F, G

Here, we'll make use of set notations

U -> Union

Example is A U B which means an occurrence that happens in either A or B

n -> Intersection

Example is A n B which means an occurrence that happens in A and B.

It can also be written as AB

' -> Complement

Example is A' which means an event where A doesn't occur.

Here, we have to prove that none of the event occur,

This means that;

E doesn't occur

F doesn't occur

G doesn't occur.

So, the notation is (E U F U G)'

Learn more about events here: https://brainly.com/question/14787733

#SPJ4

The annual investment amount required to accumulate a reserve fund of $50,000 in 10 years, assuming an annual return of 5%, is approximately $3,720.

To calculate this, we can use the formula for the future value of an ordinary annuity: \[FV = P \times \left( \frac{{(1 + r)^n - 1}}{r} \right),\] where \(FV\) is the future value (desired reserve fund amount), \(P\) is the annual investment amount, \(r\) is the annual interest rate (in decimal form), and \(n\) is the number of years. Rearranging the formula to solve for \(P\), we have: \[P = \frac{{FV \times r}}{{(1 + r)^n - 1}}.\]Substituting the given values into the formula, we get: \[P = \frac{{50000 \times 0.05}}{{(1 + 0.05)^{10} - 1}} \approx 3720.\]Therefore, the business owner would need to invest approximately $3,720 annually to accumulate a reserve fund of $50,000 at the end of 10 years, assuming a 5% annual return.

Learn more about numbers here: brainly.com/question/13045235

#SPJ11

Answer:

See Explanation

Step-by-step explanation:

The question is incomplete, as the required data to answer the question are missing.

However, the interpretation of the question is to determine the interquartile range (IQR) of a certain dataset.

Then get the difference between the calculated IQR & Joe's data and also the difference between the calculated IQR & Sam's data

Then, make comparison

To do this, I will use the following assumed datasets.

\(Data: 62, 63, 64, 64, 70, 72, 76, 77, 81, 81\)

IQR is calculated as:

\(IQR = Q_3 - Q_1\)

\(Q_3\) is \(the\ median\) of the upper half

\(Q_1\) is \(the\ median\) of the lower half

For Joe, we have:

\(Lower\ half: 62, 63, 64, 64, 70\)

\(Upper\ half: 72, 76, 77, 81, 81\)

The median is then calculated as:

\(M = \frac{N + 1}{2}\)

For, the lower half:

\(Q_1 = \frac{5 + 1}{2} = \frac{6}{2} = 3rd\)

So:

\(Q_1 = 64\)

For the upper half:

\(Q_3 = \frac{5 + 1}{2} = \frac{6}{2} = 3rd\)

So:

\(Q_3 = 77\)

When the same process is applied to Sam's data,

\(Q_1 = 52\)

\(Q_3 = 58\)

\(IQR = Q_3 - Q_1\)

\(IQR = 77 - 64\)

\(IQR = 13\)

Assume that:

\(Joe = 60\)

\(Sam = 65\)

\(Joe - IQR = 60 - 13 = 47\)

\(Sam- IQR = 65- 13 = 52\)

Hence, the IQR is 47 points less for Joe's data than Sam's

The form of the particular solution of the differential equation x" — x' – 2x = e^t cost – t^2 + cos 3t is x_p(t) = Ae^t cos(t) + Be^t sin(t) + Ct^2 + Dt + Ecos(3t) + Fsin(3t) and the particular solution of the y" – y' + 2y = (2x + 1)e^(x/2) cos (√7/2)x + 3(x^3 – x)e^(x/2) sin (√7/2) x is y_p(x) = (Ae^(x/2) cos(√7/2)x + Be^(x/2) sin(√7/2)x) + (C x^3 + Dx^2 + Ex + F)

Explanation: -

Part (a): -To determine the form of a particular solution to x" - x' - 2x = e^t cos(t) - t^2 + cos(3t),

we look at the non-homogeneous terms on the right-hand side. We see that we have a term of the form e^t cos(t), which suggests a particular solution of the form Ae^t cos(t) or Be^t sin(t).

We also have a polynomial term t^2, which suggests a particular solution of the form At^2 + Bt + C. Finally, we have a term of the form cos(3t), which suggests a particular solution of the form D cos(3t) + E sin(3t).

Thus,

x_p(t) = A e^t cos(t) + B e^t sin(t) + Ct^2 + Dt + E cos(3t) + F sin(3t) is particular solution of the above differential equation.

Part (b): -To determine the form of a particular solution to y" - y' + 2y = (2x + 1)e^(x/2) cos(√7/2)x + 3(x^3 - x)e^(x/2) sin(√7/2)x, we first observe that the right-hand side includes a product of exponential and trigonometric functions. Therefore, a particular solution may take the form of a linear combination of functions of the form e^(ax) cos(bx) and e^(ax) sin(bx).

Additionally, the right-hand side includes a polynomial of degree 3, so we may include terms of the form ax^3 + bx^2 + cx + d in our particular solution.

Overall, a possible form for a particular solution to this differential equation is:

y_p(x) = (Ae^(x/2) cos(√7/2)x + Be^(x/2) sin(√7/2)x) + (C x^3 + Dx^2 + Ex + F)

Know more about the "Particular solution" click here:

https://brainly.com/question/15127193

#SPJ11

The person's total salary over the first 6 years is $231,750.

To determine the person's total salary over the first 6 years, we need to calculate the sum of the salary for each year.

Given information:

- Initial salary: $34,000

- Annual raise: $1,850

- Number of years: 6

To calculate the total salary, we can use the arithmetic progression formula:

[ S = frac{n}{2} left(2a + (n - 1)dright) ]

Where:

- ( S ) is the sum of the salaries

- ( n ) is the number of terms (years)

- ( a ) is the first term (initial salary)

- ( d ) is the common difference (annual raise)

Substituting the given values, we have:

[ S = frac{6}{2} left(2(34000) + (6 - 1)(1850)right) ]

Simplifying the expression:

[ S = 3 left( 68000 + 5 times 1850 right) ]

[ S = 3 left( 68000 + 9250 right) ]

[ S = 3 times 77250 ]

[ S = 231750 ]

Therefore, the person's total salary over the first 6 years is $231,750.

Learn more about arithmetic progression from :

https://brainly.com/question/6561461

#SPJ11

The outward flux of the vector field F across the boundary of the region D, which is the cube bounded by the planes x = ±1, y = ±1, and ±1, can be found using the divergence theorem.

The outward flux is the integral of the divergence of F over the volume enclosed by the boundary surface.The first step is to calculate the divergence of F. The divergence of a vector field F = P i + Q j + R k is given by div(F) = ∂P/∂x + ∂Q/∂y + ∂R/∂z. In this case, div(F) = ∂/∂x(5y - 4x) + ∂/∂y(-4z - 5y) + ∂/∂z(-3y - 2x). Simplifying these partial derivatives, we have div(F) = -4 - 2 - 3 = -9.

Applying the divergence theorem, we can relate the flux of F across the boundary surface to the triple integral of the divergence of F over the volume enclosed by the surface. Since D is a cube with sides of length 2, the volume enclosed by the surface is 2^3 = 8.

Therefore, the outward flux of F across the boundary of D is given by ∬S F · dS = ∭V div(F) dV = -9 * 8 = -72. The negative sign indicates that the flux is inward.

In summary, the outward flux of the vector field F across the boundary of the cube D, as described by the given vector components, is -72. This means that the vector field is predominantly flowing inward through the boundary of the cube.

Learn more about integral here: https://brainly.com/question/31433890

#SPJ11

h = 11.9 cm

cos = adjacent/ hypotenuse

therefore:

cos(24) = h/ 13

rearrange:

h = 13cos(24)

put into calculator:

h = 11.8760...

rounded to one decimal point:

h = 11.9cm

Answer:

2S + J = 24000

Step-by-step explanation:

let Susan be S

let Jinan be J

they paid 24000

susan paid twice as muh as jinan did​

2S + J = 24000

therefore equation is

2S + J = 24000

Answer:

9

Step-by-step explanation:

63 divided 7=9

A survey is given to a random sample of some of the freshman students at a certain high school therefore the statement about the results of the survey which is true is that the responses can be used to make valid inferences about the entire freshman class at that school which is therefore denoted as option A.

This is referred to as a method of gathering information using relevant questions from a sample of people with the aim of understanding populations as a whole.

Since the survey was given to random freshman in that school, then it means that it is unbiased and will provide a valid information about them in that particular school.

Read more about Survey here https://brainly.com/question/25257437

#SPJ1

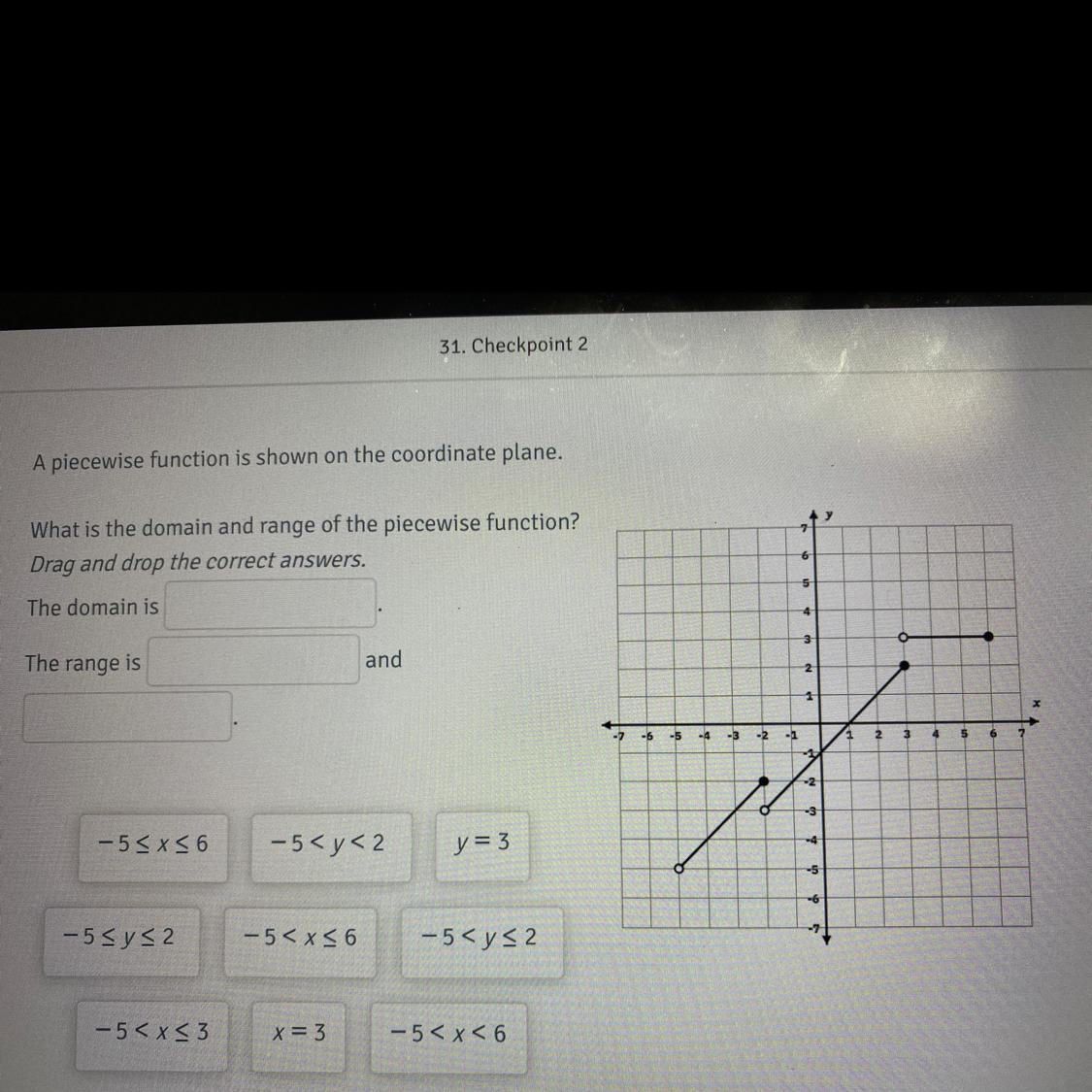
Answer:

See below

Step-by-step explanation:

Domain is the values of x a graph can have

-5 < x <= 6

Range is the y-values a graph can have

-5 < y <= 3

Answer: 2

Step-by-step explanation:

\((-3+5)^0=2\)

(a) The center of the sphere is in the first octant and is tangent to the xz-plane and to the yz-plane. This means that the center of the sphere is at a point of the form (a,b,5) where a,b≥0. The distance from the origin to the center of the sphere is  \(\sqrt{43}\), so we have \(x^{2} +x^{2} +(5-0)^{2} =43\) This gives us \(a^{2} +b^{2} =38\)

The radius of the sphere is the distance from the center of the sphere to the point where the sphere touches the xz-plane. This distance is equal to the length of the hypotenuse of a right triangle with legs of length a and b. Therefore, the radius of the sphere is \(\sqrt{a^{2}+ b^{2} } =\sqrt{38}\)

The equation of the sphere is \((x-a)^{2}+ (y-b)^{2}+ (z-5)^{2} =38\)

(b) The point where the sphere touches the xz-plane is (a,0,5). The distance between the origin and this point is \(\sqrt{a} ^{2}+\sqrt(5-0)^{2} =\sqrt{a^{2} +25}\)

Learn more about hypotenuse here:

brainly.com/question/16893462

#SPJ11

Answer:

\(64 {a}^{3} {b}^{6} = 16a {b}^{3} \times h\)

\( \frac{64 {a}^{3} {b}^{6} }{16a {b}^{3} } = h\)

\(4 {a}^{2} {b}^{3} = h\)

Answer:2.43

Step-by-step explanation:

Using translation concepts, the value of k is given as follows:

B) 1/5.

A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.

In this graph, we have that g(x) = f(kx), hence since g(-2) = f(-10):

-2 = -10k

k = 2/10

k = 1/5.

Hence option B is correct.

More can be learned about translation concepts at https://brainly.com/question/4521517

#SPJ1

No, it is simply the likelihood that the interval would include the population of the important quantity. Even though it is unlikely, it is possible that the 95% confidence interval does not include the desired population size.

The mean of your estimate plus and minus the range of that estimate constitutes a confidence interval.

You have a 5% probability of being incorrect with a 95% confidence interval. You have a 10% probability of being incorrect with a 90% confidence interval. A 95% confidence interval is narrower than a 99% confidence interval (for example, plus or minus 4.5 percent instead of 3.5 percent).

No, it is simply the likelihood that the interval would include the population of the important quantity. Even though it is unlikely, it is possible that the 95% interval does not include the desired population size.

No, it is merely the chance that the population of the significant quantity would be present during the interval. Although uncommon, there is a chance that the target population size is not included in the 95% interval.

To read more about confidence intervals, visit https://brainly.com/question/24131141

#SPJ4

To calculate the present value of Ahmed's payments, we need to discount each annual payment back to the present using the appropriate discount rate. In this case, the discount rate is the interest rate of 8%. The formula to calculate the present value of an annuity is:

PV = Payment × [(1 - \((1 + r)^{(-n)\)) / r],

where PV is the present value, Payment is the annual payment, r is the interest rate, and n is the number of periods.

Plugging in the values from the given information:

Payment = BD 5700

Interest rate (r) = 8% or 0.08

Number of periods (n) = 12

Using the formula, we can calculate the present value:

PV = BD 5700 × [(1 - \((1 + 0.08)^{(-12)\)) / 0.08]

Calculating this equation, the present value of Ahmed's payments is approximately BD 46,392.10. Therefore, the correct answer is BD 46,392.10.

Learn more about Interest rate here:

https://brainly.com/question/28272078

#SPJ11

with 4 df.

The correct answer is d. Two-sample t test with 9 df.

Answer:

125

Step-by-step explanation:

60 percent of 125=75

Answer:

should be 4 and 9/12

Step-by-step explanation:

+$+$+$+$++$+$+#++#+#+$+

To find the maximum area of the lawn that can be watered by the sprinkler, we can use the formula for the area of a circle:

A = πr^2

Given that the radius of the sprinkler's spray is 22ft, we can substitute this value into the formula:

A = 3.14 * (22)^2

A ≈ 3.14 * 484

A ≈ 1519.76

Rounded to the nearest tenth, the maximum area of the lawn that can be watered by the sprinkler is approximately 1519.8 ft^2.\(\huge{\mathcal{\colorbox{black}{\textcolor{lime}{\textsf{I hope this helps !}}}}}\)

♥️ \(\large{\textcolor{red}{\underline{\texttt{SUMIT ROY (:}}}}\)

Based on the scatter plot, the meaning of the slope in this scenario is that: The slope of the line of best fit is 0.25. Each time the shoe size increases by one, the height increases by 0.25 inches.

In this scenario, the woman's shoe size would be plotted on the x-axis of the scatter plot while her height would be plotted on the y-axis of the scatter plot.

From the Excel sheet, you should right click on a data point on the scatter plot, select format trend line (line of best fit) and then tick the box to display an equation for the line of best fit on the chart.

By critically observing the scatter plot (see attachment) which models the data in the given table, we can reasonably and logically deduce that an equation for the line of best fit is given by:

y = 0.25x + 66.6

In conclusion, the slope of this line is 0.25, which implies that when the shoe size is increased by one (1), the height is increased by 0.25 inches.

Read more on line of best fit here: brainly.com/question/12891189

#SPJ1