Factorize 7x3 - 21x2
Answers
Answer:
\(7x^{2}\)(\(x\)-3)
Step-by-step explanation:
\(7x^{3}\) - \(21x^{2}\)
\(7x^{2}\) goes into both terms.
Divide both terms by \(7x^{2}\).
\(7x^{2}\)(\(x\)-3)
Related Questions
HELP LOTS OF POINTS
What is true about the constant of variation for an inverse variation relationship?
It is the product of the independent variable and the square of the dependent variable.
It is the product of the independent and dependent variables.
It is the ratio of the constant of variation to the dependent variable.
It is the ratio of the dependent and independent variables.
Answers
Answer:
Step-by-step explanation:
equation for inverse variation, meaning x is inversely related to y.
\(y=\frac{k}{x}\)
Where
> k is your constant
>x is your independent variable because you always pick x,'s
>y is your dependent because you pick x and results in a y, therefore it is dependent on x
Evaluating answers:
>not A, nothing is being squared in the equation so not this answer
>Yes B (I think), because k= xy if you bring it over to the other side.
>Yes C (I think), It is a ratio(fraction) of x
>not D, I don't think it can be ratio of both variables
Help me to solve this fast ( prove it)

Answers
Step-by-step explanation:
sec⁴A + tan⁴A = 1 + (2tan²A/cos²A)
LHS = sec⁴A + tan⁴A
= (sec²A)² + (tan²A)² {using formula of a²+b²)
= (sec²A-tan²A) + 2tan²A.sec²A
= 1 + {2tan²A.(1/cos²A)}
= 1 + (2tan²A/cos²A)
the ratio is 5 to 4 so whats the rate
Answers
Answer:
= 1.25 units per unit
Step-by-step explanation:
Plz name me brainliest I would greatly appreciate it Thank You

Plz help me on thisssss

Answers
Answer: 1
Step-by-step explanation:
y = 1/4x - 9
m = 1/4
Perpendicular:
m_perp = -4
y = -4x + b
P(1; 1)
1 = -4 + b
b = 5
y = -4x + 5
(07.02) In JKL, slove for x
Answers
The values of {x} would be 38.1 units.
What is Pythagoras theorem?According to the Pythagoras theorem, we can write -
(hypotenuse)² = (base)² + (perpendicular)²
Given is a right angled triangle JKL.
We can solve for {x} using the cosine function as -
cos(27) = 34/x
x = 34/cos(27)
x = 38.1 units
Therefore, the values of {x} would be 38.1 units.
To solve more questions on right angled triangle, visit the link below -
https://brainly.com/question/12722092
#SPJ1

Someone help me please I don’t know how to do this

Answers
Step-by-step explanation:
A
y=10x
x:y=x:10x=1:10
a multiple-choice test has 8 questions, with 5 possible answers for each question. how many ways can the test be answered?
Answers
Answer:
6720
Step-by-step explanation:
⁸P5 = 8! / (8 - 5)!
⁸P5 = 8! / 3!
⁸P5 = 6720
Jada has a new puppy that weighs 9 pounds. the vet says that the puppy is now at about 20% of its adult weight. what will be the adult weight of the puppy?
Answers
The adult weight of the puppy calculated using percentage is 45 pounds .
In mathematics, a value or ratio that can be expressed as a simple fraction of 100 is known as a percentage.
When determining a percentage of a number, we should first divide it by 100 before multiplying the result by 100.
As a result, the proportion refers to a component per 100. The word percent denotes a percentage of 100.
It is represented by the symbol "%." Percentages can also be written as decimals or fractions, like in 0.6%, 0.25%, etc.
Academic grades are calculated using percentages for every subject. Ram, for example, received a 78% on his qualifying exam.
The weight of the puppy is 9 pounds.
This is 20% of the adult weight.
Let the adult weight be x.
therefore 20% of x = 9
Calculating we get x = 45 pounds
Hence the adult weight of the puppy is 45 pounds.
To learn more about percentage visit:
https://brainly.com/question/24159063
#SPJ4
could you help me by chance?

Answers
Answer:
27.5
This is because you plug the numbers into the equation. Hope this helps!
Find the surface area of a cylinder with a base radius of 4 in and a height of 6in. Please help no links.

Answers
Answer:
A≈ 251.33in² ok
Answer:
251.33
Step-by-step explanation:
A=2πrh+2πr2=2·π·4·6+2·π·42≈251.32741
A
shift worker clocks in at 1730 hours and clocks out at 0330 hours.
How long was the shift?
Answers
To calculate the duration of the shift, you need to subtract the clock-in time from the clock-out time.
In this case, the shift worker clocked in at 1730 hours (5:30 PM) and clocked out at 0330 hours (3:30 AM). However, since the clock is based on a 24-hour format, it's necessary to consider that the clock-out time of 0330 hours actually refers to the next day.
To calculate the duration of the shift, you can perform the following steps:
1. Calculate the duration until midnight (0000 hours) on the same day:
- The time between 1730 hours and 0000 hours is 6 hours and 30 minutes (1730 - 0000 = 6:30 PM to 12:00 AM).
2. Calculate the duration from midnight (0000 hours) to the clock-out time:
- The time between 0000 hours and 0330 hours is 3 hours and 30 minutes (12:00 AM to 3:30 AM).
3. Add the durations from step 1 and step 2 to find the total duration of the shift:
- 6 hours and 30 minutes + 3 hours and 30 minutes = 10 hours.
Therefore, the duration of the shift was 10 hours.
Enter the correct answer in the box. The graph shows function j, a transformation of f(x)= x^1/2
Answers
The required equation function j which is the transformation of \(f(x)= x^{1/2}\) is \(j(x)= (x+2)^{1/2}\) .
As we can see in the graph the functions j and f are similar but the graph of j is 2 units left of f. So, function f(x) has a domain of real number greater than equal to zero, while as the function j is 2 units left of f then its equation is given as \(j(x)= (x+2)^{1/2}\) where the domain of j is all real numbers greater then or equal to -2.
Thus, the equation of function j is the transformation of \(f(x)= x^{1/2}\) is \(j(x)= (x+2)^{1/2}\) .
Learn more about the transformation of the function here:
https://brainly.com/question/26896273
#SPJ1
In the question the graph is missing, a graph has been added on behalf of the incomplete question.

PLEASE HEELPP!!!
State the Quadratic Equation in words:
Answers
Answer:
Step-by-step explanation:
negative b plus or minus the square root of b squared minus four times a times c all over 2a
The table below contains 3 point team shooting percentages for the 2009-2010 (through February 26, 2010) for the men's teams in four of the large conference NCAA Division I basketball. An Excel file containing these data is attached (You may need to open Excel before you open this file) Are there differences between the conferences in 3 point shooting percentages and if so, where are those differences?
Answers
If you have the data available in a tabular format, you can perform statistical analysis using software such as R, Python, or Excel. Here's a general approach to analyze the data and test for differences between the conferences:
Import the data: Import the data from the Excel file into your chosen statistical software. Ensure that the data is properly formatted and organized, with each conference's 3-point shooting percentages in separate columns or as a factor variable.
Explore the data: Examine the summary statistics, such as mean, median, and standard deviation, for each conference's 3-point shooting percentages. Additionally, create visualizations, such as box plots or histograms, to observe the distribution of the data.
Test for differences: To determine if there are statistically significant differences between the conferences' 3-point shooting percentages, you can use statistical tests such as ANOVA (Analysis of Variance) or t-tests. The choice of test depends on the number of conferences and the assumptions of the data.
a. ANOVA: If you have data from more than two conferences, you can perform a one-way ANOVA test to compare the means of multiple groups simultaneously. The ANOVA test will provide an F-statistic and p-value to determine if there are significant differences between the conferences.
b. t-tests: If you want to compare the 3-point shooting percentages between specific pairs of conferences, you can perform independent t-tests between the two groups of interest. This test will provide a t-statistic and p-value to assess the significance of the difference between the means of the two groups.
Post-hoc analysis: If the ANOVA test indicates significant differences between the conferences or if you find significant differences through t-tests, you can conduct post-hoc analysis to determine which specific pairs of conferences differ significantly. Common post-hoc tests include Tukey's Honestly Significant Difference (HSD) test or pairwise t-tests with appropriate adjustments for multiple comparisons.
By following these steps, you should be able to analyze the data and identify any differences in 3-point shooting percentages between the conferences.
To know more about data visit
https://brainly.com/question/16348111
#SPJ11
What is my decimal number if I have 8 in tenths place, 2 in thousandths place and 7 in hundreds place?
Answers
Answer:
0.872
Step-by-step explanation:
8 is in the tenths place and that's the first slot for decimals then 7 is in the hundredths place and 2 in the thousandths = 0.872a poll is given, showing 61% are in favor of a new building project. let x be the number of people who favor the new building project when 25 people are chosen at random. what is the distribution of x? x ~ ? (,) please show the following answers to 4 decimal places. what is the probability that exactly 16 people out of 25 favor the new building project? what is the probability that at least 16 people out of 25 favor the new building project? what is the probability that at most 16 people out of 25 favor the new building project? what is the probability that between 12 and 19 (including 12 and 19) people out of 25 favor the new building project?
Answers
The probability that exactly 16 people out of 25 favor the new building project is 0.1285.
The probability that at most 16 people out of 25 favor the new building project is 0.3528.
The probability that between 12 and 19 (including 12 and 19) people out of 25 favor the new building project is 0.9088.
A binomial distribution is a probability distribution that describes the number of successes in a fixed number of trials, where each trial has two possible outcomes (success or failure) and the trials are independent.
The distribution of x, the number of people who favor the new building project when 25 people are chosen at random, can be modeled using a binomial distribution.
In this case, the probability of success (favoring the new building project) is 0.61, and the probability of failure (not favoring the project) is 0.39. The number of trials is 25, since we are choosing 25 people at random.
Thus, we can write x ~ Bin(25, 0.61), which means that x follows a binomial distribution with 25 trials and a probability of success of 0.61.
To find the probability that exactly 16 people out of 25 favor the new building project, we can use the binomial probability formula:
\(P(X = k) = (^n_k) * p^k * (1 - p)^{n - k}\)
where X is the random variable (in this case, the number of people who favor the project), k is the number of successes we are interested in (in this case, 16), n is the number of trials (25), p is the probability of success (0.61), and (n choose k) is the binomial coefficient, which represents the number of ways to choose k successes out of n trials.
Plugging in the values, we get:
P(X = 16) = (25 choose 16) * 0.61¹⁶ * 0.39⁹ = 0.1285
Therefore, the probability that exactly 16 people out of 25 favor the new building project is 0.1285.
To find the probability that at least 16 people out of 25 favor the new building project, we need to add up the probabilities of all the events where the number of successes is 16 or greater. We can do this using the cumulative distribution function (CDF) of the binomial distribution, which gives us the probability of X being less than or equal to a certain value.
Using a calculator or a table, we can find that P(X ≥ 16) = 0.3528.
Therefore, the probability that at least 16 people out of 25 favor the new building project is 0.3528.
To find the probability that at most 16 people out of 25 favor the new building project, we can use the complement rule, which states that the probability of an event occurring is equal to 1 minus the probability of its complement (the event not occurring). In this case, the complement event is the number of people who favor the project being greater than 16.
Using the same CDF, we can find that P(X > 16) = 0.6472. Therefore,
P(X ≤ 16) = 1 - P(X > 16) = 1 - 0.6472 = 0.3528
We can do this using the binomial probability formula for each possible value of k, and then summing the results.
P(12 ≤ X ≤ 19) = P(X = 12) + P(X = 13) + ... + P(X = 19)
Using a calculator or a table, we can find the probabilities for each value of k, and then add them up:
P(12 ≤ X ≤ 19) = 0.0309 + 0.0746 + 0.1322 + 0.1821 + 0.2001 + 0.1821 + 0.1322 + 0.0746 = 0.9088
To know more about probability here.
https://brainly.com/question/11234923
#SPJ4
Will Mark Brainliest. Please look at the other 5 questions I will post. Need this fast
Please
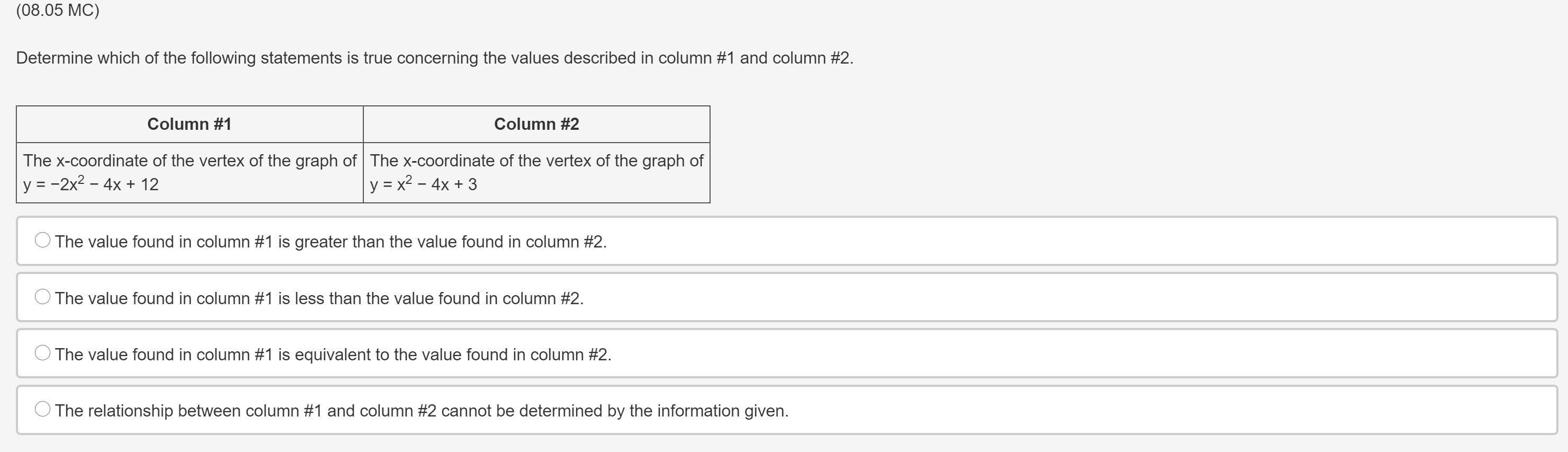
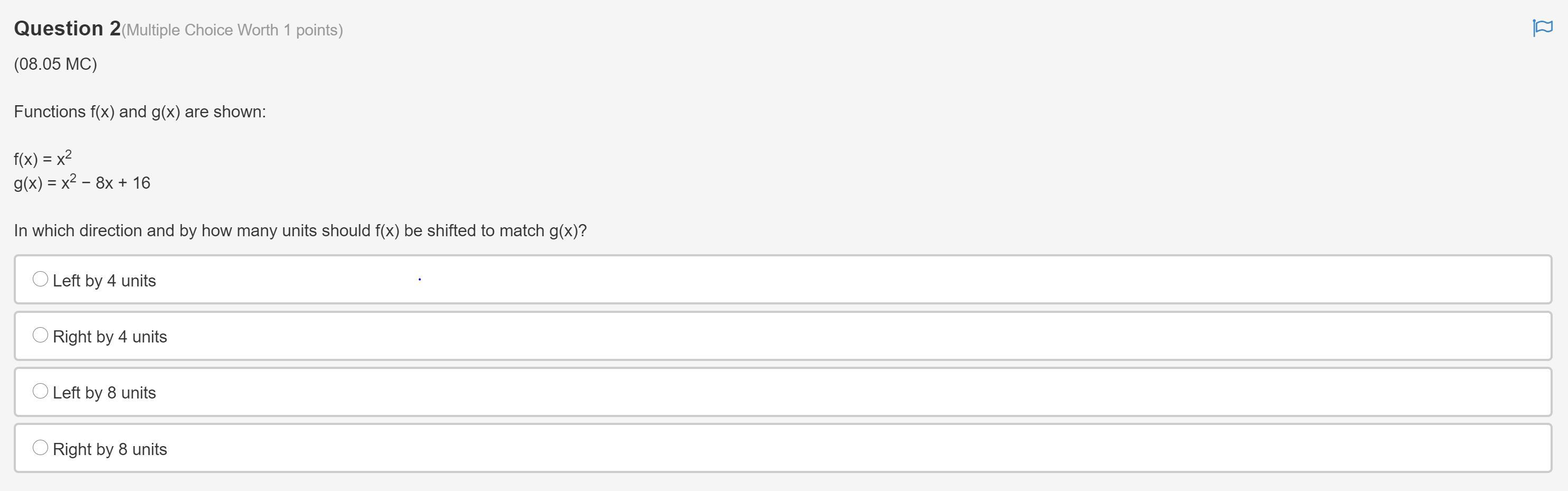

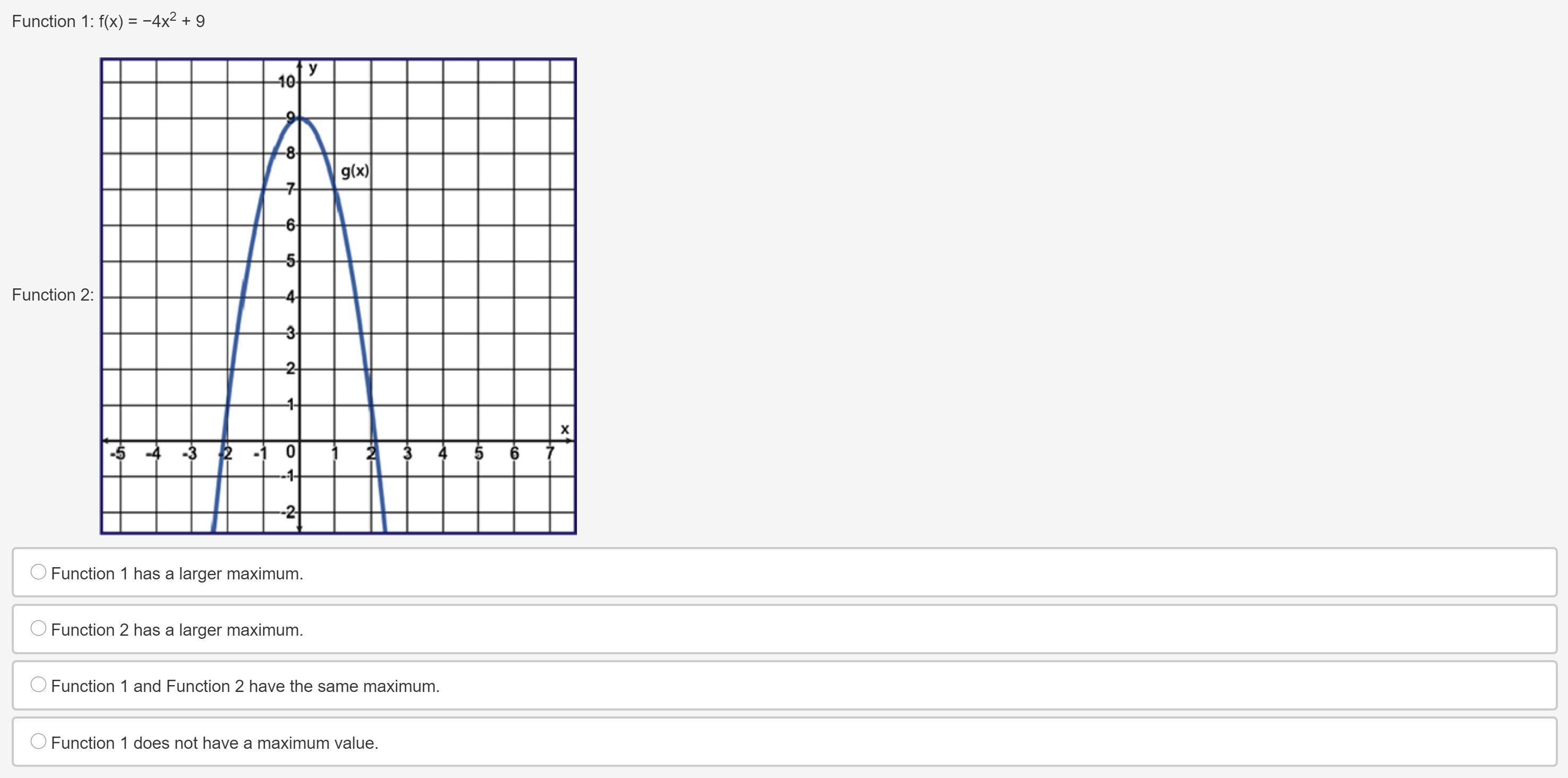
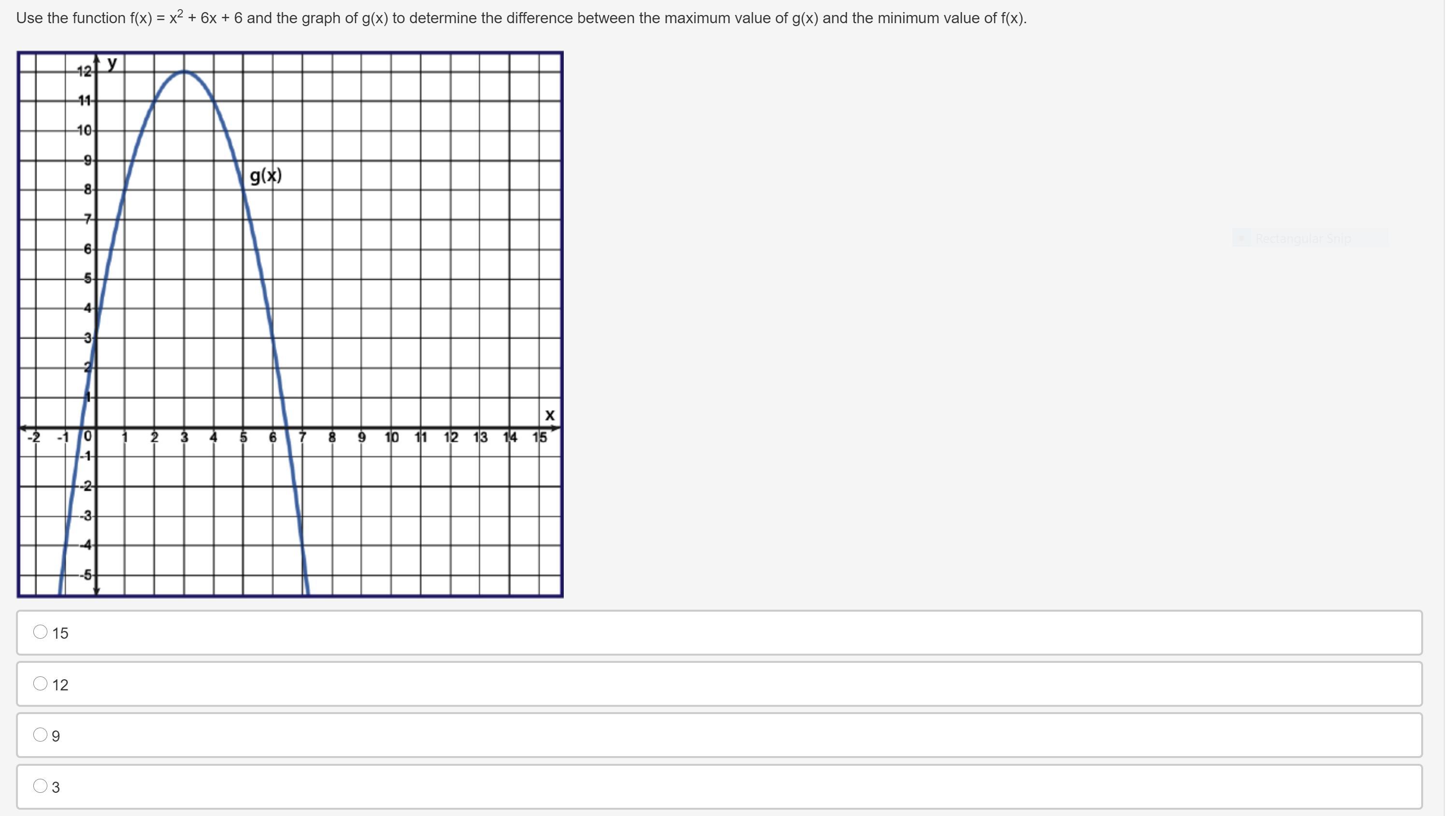
Answers
Answer:
1. Second option. Value of the first column is less than the second column's value
2. Right by 4 units
3. (-1, -6)
4. Function 1 and 2 have the same maximum
5. 15
Step-by-step explanation:
1. look at the photo
2. look at the photo
3. look at the photo
4. I used the formula -b/2a to find the x-value of the vertex. I got 0 (there is no b) and then I subbed it into the function and y = 9. Hence the vertex of the first function is (0,9) which is the same as the second function
5. The vertex of the f(x) is (-3, -3) and the vertex of g(x) is (3, 12). To find the difference you would do 12 - (-3), which would become 12 + 3 = 15

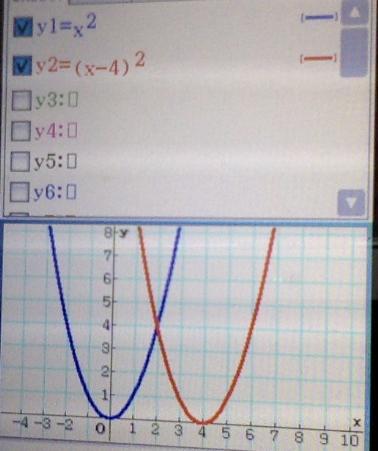
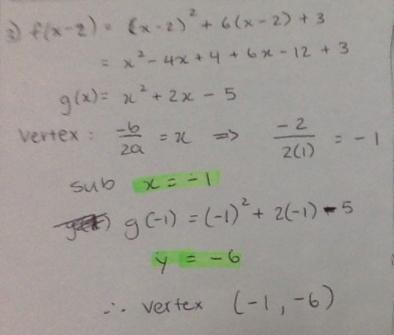
Miranda mixed 34.5 fluid ounces of blue paint, 40.5 fluid ounces of red paint, and 2 fluid ounces of black paint to make purple paint. She poured the same amount of the purple paint into 14 jars. How much paint did she pour in each jar
Answers
Answer:
5.5
Step-by-step explanation:
Miranda mixes 34.5 fluid ounces of blue paint
40.5 fluid ounces of red paint.
2 fluid ounces of black paint to produce a purple paint
She pours this purple paint into 14 jars
Therefore the amount of paint in each jar can be calculated as follows
= 34.5 + 40.5 + 2
= 77/14
= 5.5 fluid ounces
Hence there are 5.5 fluid ounces of purple paint in each jar
Answer:
5.5
Step-by-step explanation:
What is the relationship between a 90% confidence interval around a mean and a 95% confidence interval around a mean?
a. The 90% C.I. is wider and includes more values than the 95% C.I.
b. The 95% C.I. is more precise in estimating a mean than the 90% C.I.
c. The 90% C.I. is more precise in estimating a mean than the 95% C.I.
d. The 95% C.I. is narrower and includes less values than the 90% C.I.
Answers
The relationship between a 90% confidence interval around a mean and a 95% confidence interval around a mean is (b) The 95% C.I. is more precise in estimating a mean than the 90% C.I.
You have a 5% probability of being incorrect with a 95% confidence interval. You have a 10% probability of being incorrect with a 90% confidence interval.
The upper and lower numbers of a range with a 95% confidence interval (CI) of the mean are determined from a sample. This range describes potential possibilities for the mean because the actual population mean is unknown. Hence, the 95% C.I. is more precise in estimating a mean than the 90% C.I.
To learn more about confidence interval here:
https://brainly.com/question/24131141
#SPJ4
What is -3 times 4??
Answers
Answer:
-12
Step-by-step explanation:
hope it helps
have a nice evening
Fastco Corp. reports net income of $12,000, and other comprehensive loss of $3,000 (net of tax) for the year ended December 31, 2020. The December 31, 2020, balance in accumulated other comprehensive income is $6,800 (credit balance) and the balance in retained earnings is $60,000 (credit balance). The ending balance in accumulated other comprehensive income on December 31, 2019 is
Answers
The ending balance in accumulated other comprehensive income on December 31, 2019, is $10,200 (credit balance).
To determine the ending balance in accumulated other comprehensive income on December 31, 2019, we need to analyze the changes in comprehensive income and other comprehensive loss. The net income of $12,000 and other comprehensive loss of $3,000 (net of tax) for the year ended December 31, 2020, indicate that the comprehensive income for the year is $9,000 ($12,000 - $3,000).
The ending balance in accumulated other comprehensive income can be calculated by adding the comprehensive income for the year to the beginning balance in accumulated other comprehensive income. Given that the ending balance on December 31, 2020, is $6,800 (credit balance), we can derive the beginning balance in accumulated other comprehensive income on December 31, 2019, by subtracting the comprehensive income for the year ($9,000) from the ending balance on December 31, 2020. Therefore, the ending balance in accumulated other comprehensive income on December 31, 2019, is $10,200 (credit balance).
Learn more about loss here:
https://brainly.com/question/30208753
#SPJ11
how many spherical balls of diameter 15cm can be covered by 40 square metres of material
Answers
Answer:
It's very simple: divide the 40 m² area by area of 1 one sphere
\( \frac{40 \: m {}^{2} }{3.41 \times 15m {}^{2} } = 565\)
What are the values of r and sum k = 1 to 6 1/4 * (2) ^ (k - 1) for a_{1}
Answers
Answer:
r=2 and a1=1/4 so option c is correct
Step-by-step explanation:
I got it right on edge
Create graph of a function that satisfies the following: ∗f ′
(1)=0,f ′
(3)=0,f ′
(8)=0, ∗f ′
(x)<0 on (−[infinity],1) and (3,8) ∗f ′
(x)>0 on (1,3),(8,[infinity])
Answers
Given: f ′(1)=0,f ′(3)=0,f ′(8)=0,f ′(x)<0 on (−∞,1) and (3,8)f ′(x)>0 on (1,3),(8,∞)Let's first list out all the given information in the form of a table: We know that f ′(1) = 0, f ′(3) = 0, and f ′(8) = 0.
From this information we can say that the critical points of f(x) are at x = 1, 3, and 8. Now we know that f ′(x) is negative on (−∞,1) and (3,8), and it's positive on (1,3),(8,∞).
Therefore, we know that f(x) is decreasing on (−∞,1) and (3,8), and it's increasing on (1,3),(8,∞). Now let's look at the conditions given for the first derivative of f(x): f ′(x)<0 on (−∞,1) and (3,8) f ′(x)>0 on (1,3),(8,∞)
We can use this information to create the following graph:
The critical points of f(x) are at x = 1, 3, and 8. Between x = 1 and x = 3, f(x) is increasing. Between x = 3 and x = 8, f(x) is decreasing. Finally, for x < 1 and x > 8, f(x) is increasing.
To know more about derivative visit :-
https://brainly.com/question/25324584
#SPJ11
Lonna's rectangle measures 2 1/4 units by 4 1/2 units. what is the area?
Answers
\(\mathsf\blue{♧ANSWER♧}\)
Area = length × width
\( \mathsf \green{4 \frac{1}{2} \times 2 \frac{1}{4} }\)
\( \orange \implies \mathsf \green{ \frac{9}{2} \times \frac{9}{4} }\)
\( \orange \implies \mathsf \green{ \frac{81}{8} = 10.125}\)
\( \mathsf \blue{10.125 \: square \: units}\)
The city of Paris, France is completely contained within an almost circular road that goes around the edge. Use the map with its scale to estimate the circumference and area of Paris.
Use 3.14 to estimate π and round your answer to the nearest whole number.
a. The circumference of Paris is about ______ MIles
b. The circumference of Paris is about ______ mi2
Answers
Complete Question:
The city of Paris, France is completely contained within an almost circular road that goes around the edge. The radius is 3 miles. Use the map with its scale to estimate the circumference and area of Paris.
(See attachment for map)
Answer:
\(C = 18.84\ miles\)
\(A = 28.26\ miles^2\)
Step-by-step explanation:
Given
\(Radius = 3\ miles\)
Solving (a): Circumference
Circumference (C) is calculated as thus:
\(C = 2\pi r\)
Where
\(r = radius = 3\)
and
\(\pi = 3.14\)
So:
\(C = 2 * 3.14 * 3\)
\(C = 18.84\ miles\)
Hence, the circumference is about 18.84 miles
Solving (b): Area
Area (A) is calculated as thus:
\(A = \pi r^2\)
Where
\(r = radius = 3\)
and
\(\pi = 3.14\)
\(A = 3.14 * 3^2\)
\(A = 3.14 * 9\)
\(A = 28.26\ miles^2\)
Hence, the area is about 28.26 mi²

Circumference and Area of Paris is 18.84 mile and 28.26 miles²
Given that;According to map
Radius of Paris = 3 miles
Find:Circumference of Paris = 2πr
Area of Paris = πr²
Circumference of Paris in miles = 2(3.14)(3)
Circumference of Paris in miles = 18.84 miles
Area of Paris = πr²
Area of Paris = (3.14)(3)²
Area of Paris = (3.14)(9)
Area of Paris = 28.26 miles²
Learn more:https://brainly.com/question/5308025?referrer=searchResults
Which inequality is true?

Answers
C, because π ≈ 3,14 so 9π = 9 · 3,14 = 28,26 > 27
a cylinder has a height of 12 feet and a radius of 14 feet. what is its volume? use ≈ 3.14 and round to the nearest hundredth
Answers
Answer:
V = 7385.28
Step-by-step explanation:
Formula of the volume of a cylinder: V = pi*r^2*h
Since you are told to replace pi with 3.14, now plug in the numbers that you are given into the formula...
V = (3.14)(14)^2*(12)
= 7385.28
Notes: Remember you always have to divide your radius in half if it gives you a diameter, BUT since in this question it's given, you don't have to do any extra work :)
Consider the following system of equations.
x+2 z=-1
y-2 z=2
2 x+y+z=1
b. Find the determinant of the matrix A .
Answers
The determinant of the matrix A can be found by arranging the coefficients of the variables in the system of equations into a matrix and evaluating its determinant.
The given system of equations can be written in matrix form as follows:
```
| 1 0 2 | | x | | -1 |
| 0 1 -2 | * | y | = | 2 |
| 2 1 1 | | z | | 1 |
```
The matrix on the left side is denoted as matrix A. To find the determinant of matrix A, we can use the cofactor expansion method or row operations. In this case, let's use the cofactor expansion along the first row.
Expanding along the first row, the determinant of A can be calculated as:
det(A) = (1) * det(A₁₁) - (0) * det(A₁₂) + (2) * det(A₁₃)
Where A₁₁, A₁₂, and A₁₃ are the determinants of the submatrices obtained by removing the first row and the respective column from matrix A.
Calculating the determinants of the submatrices, we have:
det(A) = (1) * (1 - 2) - (0) * (2 - 2) + (2) * (2 - 2)
Simplifying, we find:
det(A) = -1 + 0 + 0 = -1
Therefore, the determinant of matrix A is -1.
Learn more about determinant here:
https://brainly.com/question/14405737
#SPJ11
Consider the following linear programming problem:Maximize 6x+5y (OBJ)Subject tox+y≤6 (1)2x+y≤8 (2)y≤5 (3)
Answers
The maximum value of the objective function is 33, which occurs at the corner point (3, 3)
According to the question we have to maximize 6x+5y (OBJ)Subject tox+y≤6 (1)2x+y≤8 (2)y≤5 (3).Linear programming is a mathematical method that aims to maximize or minimize an objective function subject to a set of linear constraints. In this problem, we are asked to maximize the objective function 6x + 5y subject to the constraints given by the inequalities 1, 2, and 3.
The inequalities 1, 2, and 3 define a feasible region in the xy-plane, which is a region that satisfies all the constraints. The feasible region can be found by graphing the three inequalities and shading in the region that satisfies all of them.
In this case, the feasible region is a triangle with vertices (0, 0), (3, 3), and (4, 1), as shown below:
The objective function 6x + 5y is evaluated at each corner point as follows:
At (0, 0), 6(0) + 5(0) = 0, At (3, 3), 6(3) + 5(3) = 33, At (4, 1), 6(4) + 5(1) = 29. Thus, the optimal solution is x = 3 and y = 3, and the maximum value of the objective function is 33.
To know more about linear programming problem, click here:
https://brainly.com/question/29997614
#SPJ11