Express 0.bar 36 in p/q form is
Answers
Step-by-step explanation:
4/11
please check the image above for confirmation

Answer:
.
Step-by-step explanation:
Express \(\sf0.\overline{36}\) in p/q form
\(\large\underline{\sf{Solution-}}\)
Given that:
\(\longmapsto\sf0.\overline{36}\)
Let this be equal to x.
So,
\(\longmapsto\sf x=0.\overline{36}- - - -(1)\)
Multiplying both side by 100,
\(\longmapsto\sf 100x=36.\overline{36}- - - -(2)\)
Subtracting (2) from (1),
\(\longmapsto\sf 100x-x=36.\overline{36}-0.\overline{36}\)
\(\longmapsto\sf 99x=36\)
So,
\(\longmapsto\sf x=\dfrac{36}{99}\)
Dividing by 9,
\(\sf\longmapsto x=\dfrac{4}{11}\)
Hence,
\(\sf\longmapsto\bf0.\overline{36}=\dfrac{4}{11}\)
Related Questions
A study was commissioned to find the mean weight of the residents in certain town.
The study found the mean weight to be 187 pounds with a margin of error of 3
pounds. Which of the following is not a reasonable value for the true mean weight of
the residents of the town?
Answers
The value that is not reasonable for the true mean weight of the residents of the town is 193 pounds
Given that the mean weight is 187 pounds with a margin of error of 3 pounds, we can construct the interval as follows:
Mean weight - Margin of error = 187 - 3 = 184 pounds
Mean weight + Margin of error = 187 + 3 = 190 pounds
So, the reasonable range for the true mean weight of the residents of the town is between 184 and 190 pounds.
Now, let's evaluate the options to identify the value that falls outside this reasonable range:
A. 170 pounds - This value falls below the lower limit of the reasonable range (184 pounds). Therefore, it is not a reasonable value for the true mean weight.
B. 188 pounds - This value falls within the reasonable range of 184 to 190 pounds. It is a reasonable value.
C. 193 pounds - This value falls above the upper limit of the reasonable range (190 pounds). Therefore, it is not a reasonable value for the true mean weight.
D. 186 pounds - This value falls within the reasonable range of 184 to 190 pounds. It is a reasonable value.
E. 182 pounds - This value falls below the lower limit of the reasonable range (184 pounds). Therefore, it is not a reasonable value for the true mean weight.
From the options provided, the value that is not reasonable for the true mean weight of the residents of the town is 193 pounds.
Learn more about Margin of Error here:
https://brainly.com/question/16981466
#SPJ1
simplify 321/99 fractions
Answers
Answer:
107/33
Step-by-step explanation:
How many 1/8-foot pieces of ribbon can be cut from a roll of ribbon that is 2 1/2
feet long?
A. 20
B. 11
C. 10
D. 22
Answers
Answer:
A. 20
Step-by-step explanation:
We know that there are 8 eights in a whole, and a whole is equal to the number 1. The number 2 consists of two wholes, and so we multiply 8 by 2.
8 wholes in each 1 × 2 ones = 16 wholes
Now, we know that the number 2 is equal to 16 wholes, so now we need to find how much 1/2 of a whole is worth.
1 whole = 8 eights, so divided by 2, it would be 4 eights for a half of a whole.
So, we add 16 + 4 to get the result of 20.
Please help me with this.

Answers
Here are the correct matches to the expressions to their solutions.
The GCF of 28 and 60 is 4.
(-3/8)+(-5/8) = -4/4 = -1.
-1/6 DIVIDED BY 1/2 = -1/6 X 2 = -1/3.
The solution of 0.5 x = -1 is x = -2.
The solution of 1/2 m = 0 is m = 0.
-4 + 5/3 = -11/3.
-2 1/3 - 4 2/3 = -10/3.
4 is not a solution of -4 < x.
1. The GCF of 28 and 60 is 4.
The greatest common factor (GCF) of two numbers is the largest number that is a factor of both numbers. To find the GCF of 28 and 60, we can factor each number completely:
28 = 2 x 2 x 7
60 = 2 x 2 x 3 x 5
The factors that are common to both numbers are 2 and 2. The GCF of 28 and 60 is 2 x 2 = 4.
2. (-3/8)+(-5/8) = -1.
To add two fractions, we need to have a common denominator. The common denominator of 8/8 and 5/8 is 8. So, (-3/8)+(-5/8) = (-3 + (-5))/8 = -8/8 = -1.
3. -1/6 DIVIDED BY 1/2 = -1/3.
To divide by a fraction, we can multiply by the reciprocal of the fraction. The reciprocal of 1/2 is 2/1. So, -1/6 DIVIDED BY 1/2 = -1/6 x 2/1 = -2/6 = -1/3.
4. The solution of 0.5 x = -1 is x = -2.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate x by dividing both sides of the equation by 0.5. This gives us x = -1 / 0.5 = -2.
5. The solution of 1 m = 0 is m = 0.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate m by dividing both sides of the equation by 1. This gives us m = 0 / 1 = 0.
6. -4 + 5/3 = -11/3.
To add a fraction and a whole number, we can convert the whole number to a fraction with the same denominator as the fraction. In this case, we can convert -4 to -4/3. So, -4 + 5/3 = -4/3 + 5/3 = -11/3.
7. -2 1/3 - 4 2/3 = -10/3.
To subtract two fractions, we need to have a common denominator. The common denominator of 1/3 and 2/3 is 3. So, -2 1/3 - 4 2/3 = (-2 + (-4))/3 = -6/3 = -10/3.
8. 4 is not a solution of -4 < x.
The inequality -4 < x means that x must be greater than -4. The number 4 is not greater than -4, so it is not a solution of the inequality.
For more such questions on GCF
https://brainly.com/question/902408
#SPJ8
10 workers can create 20 products in 40days. all workers are equally productive. A company has only 5 workers.
how many days will it take to create all 20 products?
Answers
The number of days it will take 5 workers to create 20 products, found using the work rate for 1 worker is 80 days
What is the work rate of 1 worker?Work rate is the rate at which a specified work is completed.
The number of days it will take 10 workers to create 20 products = 40 days
Therefore;
The number of days it will take 1 worker to create 20 products = 40 × 10 days = 400 days
Where 1 worker can create 20 products in 400 days, then;
The work rate for one worker indicates;
The number of days it will take 5 workers to create 20 products can be found by dividing the number of days it will take 1 worker to create the 20 products by 5
5 workers will take = 400 days ÷ 5 = 80 days
The number of days it will take 5 workers to create 20 products = 80 daysLearn more about work rate here: https://brainly.com/question/26199070
#SPJ1
$10 less than the amount of the service charge
Answers
Wayne and Mack have
9 cats. Mack has twice
as many as Wayne.
How many cats does
Mack have?
Answers
Answer:
18
Step-by-step explanation:
mack has 18cats because she has 2×9 cats as Wayne 2×9 is 18
Answer:
18
Step-by-step explanation:
\(\sf Twice = *2\\9 * 2 = 18\)
plz help me i will mark brainest
what is s

Answers
Answer:
12?
Step-by-step explanation:
6/8 = 9/?
8 x 9=72
72/6= 12
Answer:
6 / 8 on the small triangle and 9 on the big one
Step-by-step explanation:
help! please give 35 points

Answers
The area of the composite figure is 378.5 square feets.
How to find the total area of the figure?We can decompose this into a rectangle of 30ft by 10ft and a circle whose diameter is 10ft.
Remember that the area of a rectangle of width W and length L is given by:
A = L*W
So the area of this rectangle is:
A = 30ft*10ft = 300ft²
And the area of a circle whose diameter D is:
A = 3.14*(D/2)²
So in this case the area of the circle is:
A = 3.14*(10ft/2)²
A = 3.14*(5ft)² = 78.5 ft²
Then the total area of the composite figure is:
area = 300ft² + 78.5 ft²
area = 378.5 ft²
Learn more about area at:
https://brainly.com/question/24487155
#SPJ1
a system of two linear equations to solve a real-world problem.
Valerie watched 6 times as many hours of television over the weekend as Diana. Together
they watched a total of 14 hours of television. Write a system of equations that represents the
situation.
Answers
Answer:
x = 6y
x + y = 14
where x & y are the number of hours Valerie and Diana watched television respectively.
Step-by-step explanation:
:)
3. i just graduated from school with $25,000 worth of debt. i want to know what my monthly payment is going to be. i was able to finance it over 7 years at 6%.
Answers
If i just graduated from school with $25,000 worth of debt. The monthly payment if you were able to finance it over 7 years at 6% is: $359.44.
How to find the monthly payment?Using the loan payment formula to find the monthly payment
Payment = Loan Amount× (Interest Rate / 12) / (1 - (1 + (Interest Rate / 12))^- (Number of Payments))
Plugging in the values:
Payment = $25,000× (0.06 / 12) / (1 - (1 + (0.06 / 12))^- (12 × 7))
Payment = $359.44
Therefore the monthly payment is $359.44.
Learn more about monthly payment here:https://brainly.com/question/2151013
#SPJ1
graph the parabola x=1/2(y-2)^2-4. find and graph the vertex, focus, directrix, and focal chord endpoints.
Answers
1. Find the graph of the parabola attached below
2. Vertex (-4, 2) Focus (-7/2, 2) Directrix (x = -9/2) Endpoints (-7/2, 1) (-7/2, 3)
How do we find the vertex, focus, directrix, and focal chord endpoints or the parabola?For the parabola, x = 1/2(y-2)² - 4 we will use the equation x = 4p(y-k)² + h,
Vertex → (h, k)
In our given equation, (y - 2) → (y - k), so k = 2. The term on the rightmost side of our equation (-4) → h in the form, so we know h = -4. ∴ vertex (-4, 2).
focus → (h, k) = (-4, 2); P = 1/2
Parabola is symmetric around the x axis and so the focus lies a distance P, from the center, along the x axis.
∴ Focus is (-4 + p, 2)
(-4 + 1/2, 2) ⇒ (-7/2, 2)
directrix → x = d
Parabola is symmetric around the x axis and therefore the directrix is a line paralled to the y axis a distance away from the ceter (-4, 2) x coordinate.
∴ x = -4 - p ⇒ x = -4 - 1/2
x = 9/2
focal chord endpoints →
The focus of the parabola is (-7/2, 2).
The y-coordinate of the focus is 2, so the y-coordinates of the endpoints of the focal chord are 2 + 1 and 2 - 1, → 3 and 1.
Therefore, the endpoints of the focal chord are:
(-7/2, 3) and (-7/2, 1).
Find more exercises on parabola;
https://brainly.com/question/11911877
#SPJ1

Construct a table of values for the following functions using the integers from -4 to 4.
a. F(x)=6/x-2
b. r(x)=6x+12/x^-4
Answers
Step-by-step explanation:
Find the table attached
a) Given
F(x) = 6/x-2
When x = -4
F(-4) = 6/-4-2
F(-4) = 6/-6
F(-4) = -1
F(x) = 6/x-2
When x = -3
F(-3) = 6/-3-2
F(-3) = 6/-5
F(-3) = -1.2
F(x) = 6/x-2
When x = -2
F(-2) = 6/-2-2
F(-2) = 6/-4
F(-2) = -1.5
F(x) = 6/x-2
When x = -1
F(-1) = 6/-1-2
F(-1) = 6/-3
F(-1) = -2.0
F(x) = 6/x-2
When x = 0
F(0) = 6/0-2
F(0) = 6/-2
F(0) = -3
F(x) = 6/x-2
When x = 1
F(1) = 6/1-2
F(1) = 6/-1
F(1) = -6
F(x) = 6/x-2
When x = 2
F(2) = 6/2-2
F(2) = 6/0
F(2) = infty
F(x) = 6/x-2
When x = 3
F(3) = 6/3-2
F(3) = 6/1
F(3) = 6
F(x) = 6/x-2
When x = 4
F(4) = 6/4-2
F(4) = 6/2
F(4) = 3
b) Given
r(x)=6x+12/x^-4
When x = -4
r(-4) = 6(-4)+12/(-4)^-4
r(-4) = -24+12/(1/256)
r(-4) = -12(256)
r(-4) = -3072
When x = -3
r(-3) = 6(-3)+12/(-3)^-4
r(-3) = -18+12/(1/81)
r(-3) = -6(81)
r(-3) = -486
When x = -2
r(-2) = 6(-2)+12/(-2)^-4
r(-2) = -12+12/(1/16)
r(-2) = -0(16)
r(-2) = 0
When x = -1
r(-1) = 6(-1)+12/(-1)^-4
r(-1) = -6+12/(1)
r(-1) = -6+12
r(-1) = 6
When x = 0
r(0) = 6(0)+12/(0)^-4
r(0) = 0+12/0
r(0) = 12/0
r(0) = infty
When x = 1
r(1) = 6(1)+12/(1)^-4
r(1) = 6+12/1
r(1) = 18(1)
r(1) = 18
When x = 2
r(2) = 6(2)+12/(2)^-4
r(2) = 12+12/1/16
r(2) = 24(16)
r(2) = 384
When x = 3
r(3) = 6(3)+12/(3)^-4
r(3) = 18+12/1/81
r(3) = 30(81)
r(3) = 2430
When x = 4
r(4) = 6(4)+12/(4)^-4
r(4) = 24+12/1/256
r(4) = 36(256)
r(4) = 9216

We want to construct tables of values for the two given functions.
The tables are:
a)
\(\left[\begin{array}{ccc}x&y\\-4&-7/2\\-3&-4\\-2&-5\\-1&-8\\0&NaN\\1&4\\2&1\\3&0\\4&-1/2\end{array}\right]\)
b)
\(\left[\begin{array}{ccc}x&y\\-4&3,048\\-3&954\\-2&180\\-1&6\\0&0\\1&18\\2&204\\3&990\\4&3,096\end{array}\right]\)
A table will be something like:
\(\left[\begin{array}{ccc}x&y\\-4&\\-3&\\-2&\\-1&\\0&\\1&\\2&\\3&\\4&\end{array}\right]\)
Where the values of x go from -4 to 4.
To complete the tables, we just need to evaluate the functions in each one of the x-values at the left, and the outcome will be placed at the right.
a) f(x) = 6/x - 2
Now we just need to evaluate the function in all the given points:
f(-4) = 6/(-4) - 2 = -3/2 - 4/2 = -7/2
f(-3) = 6/-3 - 2 = -4
f(-2) = 6/-2 - 2 = -5
f(-1) = 6/-1 - 2 = -8
f(0) is undefined, as we can't divide by zero, here we can write NaN (Not a number).
f(1) = 6/1 - 2 = 4
f(2) = 6/2 - 2 = 1
f(3) = 6/3 - 2 = 0
f(4) = 6/4 - 2 = -1/2
Now we put all of these in the correspondent place of the table:
\(\left[\begin{array}{ccc}x&y\\-4&-7/2\\-3&-4\\-2&-5\\-1&-8\\0&NaN\\1&4\\2&1\\3&0\\4&-1/2\end{array}\right]\)
b) We do the same thing, here we have:
r(x) = 6*x + 12/x^-4 = 6*x + 12*x^4
Now we evaluate this in the given values:
r(-4) = 6*(-4) + 12*(-4)^4 = 3,048
r(3) = 6*(-3) + 12*(-3)^4 = 954
r(-2) = 6*(-2) + 12*(-2)^4 = 180
r(-1) = 6*(-1) + 12*(-1)^4 = 6
r(0) = 6*0 + 120^4 = 0
r(1) = 6*1 + 12*1^4 = 18
r(2) = 6*2 + 12*2^4 = 204
r(3) = 6*3 + 12*3^4 = 990
r(4) = 6*4 + 12*4^4 = 3,096
Now we place these values in the correspondent place on the table:
\(\left[\begin{array}{ccc}x&y\\-4&3,048\\-3&954\\-2&180\\-1&6\\0&0\\1&18\\2&204\\3&990\\4&3,096\end{array}\right]\)
These are our two tables.
If you want to learn more, you can read.
https://brainly.com/question/8629807
P=x-2 ÷ x+1 for what value of x is P undefined
Answers
Answer:
x = - 1
Step-by-step explanation:
P = \(\frac{x-2}{x+1}\)
the denominator of the rational function cannot be zero as this would make it undefined. Equating the denominator to zero and solving gives the value that x cannot be.
x + 1 = 0 ( subtract 1 from both sides )
x = - 1
P is undefined when x = - 1
Write the prime factorization of 50. Use exponents when appropriate and order the factors from least to greatest (for example, 2235)
Answers
The prime factorization of 50 is:
2 x 5 x 5
In exponent notation, we can write it as:
2 x 5²
The factors are ordered from least to greatest as 2, 5, 5.
Nicholas put 1,012 baseball cards into boxes. He put 22 cards in each box. How many boxes did Nicholas need for these baseball cards?
Answers
Answer:
46 boxes
Step-by-step explanation:
1012 / 22 = 46
A cave explorer is at an elevation of −38 feet. The explorer starts moving at a rate of −12 feet per minute. The relationship between the explorer's elevation y, and her rate of decrease x, can be represented be the inequality 7 = -12x -38.
Solve the inequality to determine how many minutes it will take the explorer to reach an elevation deeper than -200 feet.
-200 \(\geq \\\) -12x - 38
Answers
Answer:
To solve this inequality, we need to isolate the x-variable on one side of the equation. To do this, we can add 38 to both sides of the equation to get the following:
-200 - 12x - 38 = 38
-200 - 12x = 76
Next, we can divide both sides of the equation by -12 to get the following:
-200 - 12x = 76
x = -17
Finally, we can use the value of x to determine how long it will take the explorer to reach an elevation deeper than -200 feet. Since the explorer moves at a rate of -12 feet per minute, it will take her 17 minutes to reach this depth.
. The table below shows the cost of making a long distance call based on the length of the call. Long Distance Rates Time (minutes) Cost 5 $0.55 6 $0.62 7 $0.69 8 $0.76 9 $0.83 10 $0.90 Refer to the above table of long distance rates. Write an expression that can be used to find the cost of an n-minute long distance call, where n is at least 5 minutes.
Answers
An expression that can be used to find the cost of an n-minute long distance call, where n is at least 5 minutes is (0.55 + (n - 5) x 0.07) dollars.
Given:
Long Distance Rates Time (minutes) Cost5 $0.556 $0.627 $0.698 $0.769 $0.8310 $0.90We need to find an expression that can be used to find the cost of an n-minute long-distance call, where n is at least 5 minutes.
The cost of making a long-distance call is given for 5 minutes, 6 minutes, 7 minutes, 8 minutes, 9 minutes, and 10 minutes.
We can observe from the above table that for every increase of 1 minute, the cost increases by $0.07.
We can conclude that the cost of n minutes long-distance call is given by: (0.55 + (n - 5) x 0.07) dollars when n is at least 5 minutes.
Therefore, the required expression is: (0.55 + (n - 5) x 0.07) dollars when n is at least 5 minutes. The above expression is based on the pattern in the table provided for long-distance call rates. We can use this expression for values of n greater than or equal to 5.
For more such questions on expression, click on:
https://brainly.com/question/723406
#SPJ8
Define confidence interval and degree of confidence. Provide at least one example of a confidence interval and interpret the result.
Answers
Answer:
confidence interval:
This tells us the degree of certainty or uncertainty that is existent in a sampling method. It gives us a range of values, telling us we are fairly sure that our true value or parameter lies within the range.
Degree of confidence:
This tells us that the confidence interval has captured the true/exact population parameter.
If we have 95% degree of confidence, we are 95% sure that that the exact/true parameter are in the confidence interval
how many ft is equal to 1.66m
Answers
Answer:
5.44 meters
Step-by-step explanation:
We Know
0.3048 meter = 1 ft
How many ft makes a height of 1.66m?
We Take
1.66 ÷ 0.3048 ≈ 5.44 meters
So, the answer is 5.44 meters.
PICK AN ANSWER!!! BRAINLIEST IF RIGHT

Answers
Answer:
Hey there!
This is an obtuse isosceles, because two sides are congruent, and one angle is greater than 90 degrees.
Let me know if this helps :)
Answer:
\(\Large \boxed{\mathrm{C. \ obtuse \ isosceles }}\)
Step-by-step explanation:
An isosceles triangle has two equal angles. This triangle has two base angles equal.
An obtuse triangle has an angle measuring greater than 90 degrees. This triangle has an angle measuring 136 degrees.
This triangle is an obtuse isosceles triangle.
In a survey of 1309 people, 825 people said they voted in a recent presidential election. Voting records show that 60% of eligible voters actually did vote. Given that 60% of eligible voters actually did vote,
(a) find the probability that among 1309 randomly selected voters, at least 825 actually did vote.
(b) What do the results from part (a) suggest?
Answers
Answer:
a) P(X>825)
b) This low value of probability of the sample outcome (as 825 voters actually did vote) suggests that the 60% proportion may not be the true population proportion of eligible voters that actually did vote.
Step-by-step explanation:
We know a priori that 60% of the eligible voters did vote.
From this proportion and a sample size n=1309, we can construct a normal distribution probabilty, that is the approximation of the binomial distribution for large samples.
Its mean and standard deviation are:
\(\mu=n\cdot p=1309\cdot 0.6=785.4\\\\\sigma =\sqrt{np(1-p)}=\sqrt{1309\cdot 0.6\cdot 0.4}=\sqrt{314.16}=17.7\)
Now, we have to calculate the probabilty that, in the sample of 1309 voters, at least 825 actually did vote. This is P(X>825).
This can be calculated using the z-score for X=825 for the sampling distribution we calculated prerviously:
\(z=\dfrac{X-\mu}{\sigma}=\dfrac{825-785.4}{17.7}=\dfrac{39.6}{17.7}=2.24\\\\\\P(X>825)=P(z>2.24)=0.0126\)
This low value of probability of the sample outcome (as 825 voters actually did vote) suggests that the 60% proportion may not be the true population proportion of eligible voters that actually did vote.
Find the missing length of the triangle.

Answers
Answer:
Pitagoras=29
Step-by-step explanation:
H2=21x21+20x20
h2=841
H=29
Calculate the missing internal angle 40 87 38

Answers
The sum of the internal angles must be equal to 360°, using that we will see that x = 195°.
How to find the missing internal angle?Here we can see a figure of 4 sides, remember that for a figure of N sides, the sum of the internal angles gives:
(N - 2)*180°
Then in this case the sum of internal angles gives:
(4 - 2)*180° = 360°
Then we can write the linear equation:
87° + 38° + 40° + x° = 360°
x° = 360°° - 87° - 38° - 40° = 195°
Learn more about internal angles:
https://brainly.com/question/24966296
#SPJ1
What is the length of AB
Please help...no links please
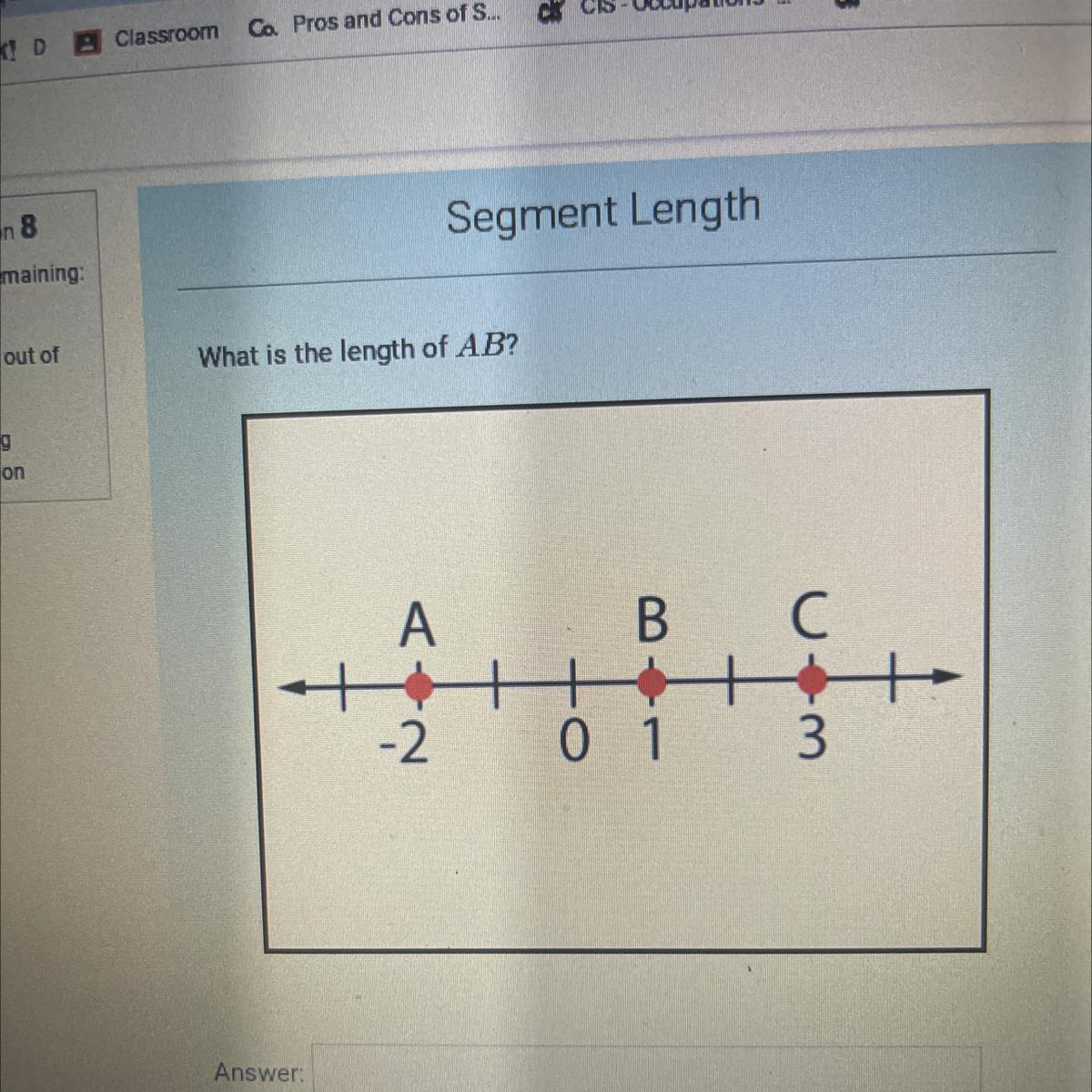
Answers
Answer:
AB = 1- (-2) = 1+2 = 3units
Write the null and alternative hypotheses you would use to answer this question. Are Americans getting fatter? Researchers interested in this question take a random sample of 500 people and record an average weight of 190 pounds. Ten years ago, the average weight was 185 pounds.
Answers
Answer:
H0: u = 185 against Ha: u > 185
or
H0: u ≤ 185 against Ha: u > 185
Step-by-step explanation:
The null and alternative hypotheses for this experiment would be
H0: u = 185 against Ha: u > 185
or
H0: u ≤ 185 against Ha: u > 185
This is a one tailed test .
If the results are such that we reject the null hypothesis and accept the alternative hypothesis it means that the Americans are getting fatter as the mean weight is increasing day by day.
The null hypothesis deals with all the values equal to or less than 185 pounds and the alternative with all the values greater than 185 pounds.
The point P=(1/2,y)lies on the unit circle shown below. What is the value of y in simplest form?
Answers
The value of y in simplest form for the point P = (1/2, y) lying on the unit circle is y = ± √(3)/2.
To find the value of y in simplest form for the point P = (1/2, y) lying on the unit circle, we can use the equation of the unit circle, which states that for any point (x, y) on the unit circle, the following equation holds: x^2 + y^2 = 1.
Plugging in the coordinates of the point P = (1/2, y), we get:
(1/2)^2 + y^2 = 1
1/4 + y^2 = 1
y^2 = 1 - 1/4
y^2 = 3/4.
To simplify y^2 = 3/4, we take the square root of both sides:y = ± √(3/4).
Now, we need to simplify √(3/4). Since 3 and 4 share a common factor of 1, we can simplify further: y = ± √(3/4) = ± √(3)/√(4) = ± √(3)/2.
for more search question point
https://brainly.com/question/28162977
#SPJ8
Riku owed his mom $13 because he forgot to do his
chores for 2 weeks. He took out the trash which was
worth $2, walked the dog which was worth $3, and
unloaded the dishwasher which was worth $1. Write an
equation that shows how much money Riku owes his
mom now.
Answers
He owes her 13 but he gave her 2+3+1 so now he owes her 7
find the square root of 22
Answers
Answer:
4.6
Step-by-step explanation:
Answer:
4.69041575982
Step-by-step explanation:
According to the fundamental theorem of algebra how many zeros does the function f x = -2x4-5x3-x+2 have
Answers
The required, given polynomial has exactly 4 roots, which may be real or imaginary or a combination of both.
What is a polynomial function?A polynomial function is a function that applies only integer dominions or only positive integer powers of a value in an equation such as the monomial, binomial, and trinomial, etc. ax+b is a polynomial.
Here,
The fundamental theorem of algebra states that every non-constant polynomial with complex coefficients has exactly as many roots (zeros) as its degree. In this case, the degree of the polynomial is 4, so it has exactly 4 complex roots.
However, it is not clear whether any of the roots are real or imaginary, or whether they are all complex. To determine this, we would need to use methods such as the rational root theorem, synthetic division, or the quadratic formula to find the roots of the polynomial.
Without actually finding the roots, we can say that the polynomial has exactly 4 roots, which may be real or imaginary or a combination of both.
Learn more about polynomial functions here:
https://brainly.com/question/12976257
#SPJ1