Answers
Answer:
Im having a good day!
Step-by-step explanation:
Sadly, my man got punched in the face by his brother, but getting my hair cut later today
Related Questions
Pls help pls helppp i will giving breanlist
Let f (x) = 7+3 and g(x) = Vx+5. What is the domain of (fºg)(x)?

Answers
Answer:
[-5, 4) ∪ (4, ∞)
Step-by-step explanation:
Given functions:
\(f(x)=\dfrac{1}{x-3}\)
\(g(x)=\sqrt{x+5}\)
Composite function:
\(\begin{aligned}(f\:o\:g)(x)&=f[g(x)]\\ & =\dfrac{1}{\sqrt{x+5}-3} \end{aligned}\)
Domain: input values (x-values)
For \((f\:o\:g)(x)\) to be defined:
\(x+5\geq 0 \implies x\geq -5\)
\(\sqrt{x+5}\neq 3 \implies x\neq 4\)
Therefore, \(-5\leq x < 4\) and \(x > 4\)
⇒ [-5, 4) ∪ (4, ∞)
what's the difference between two whole number 1/2 percent of 36 and 30% of 10
Answers
Here, we proceed step by step, to obtain our answer,
\(\frac{1}{2}\) % of 36 can be written as ,
0.5 % of 36 , which means,
100 % refers to 36, then
0.5 % refers to what, thus, by cross multiplication we get,
0.5 % of 36 = \(\frac{0.5 X 36}{100}\) = 0.18 ___(1), which can be expressed in whole numbers as 0.
Now, 30 % of 10 means,
100 % refers to 10, then
30 % refers to what, thus, by cross multiplication we get,
30 % of 10 = \(\frac{30 X 10}{100}\) = 3 __(2)
From equations (1) and (2),
the whole numbers that we obtain are 0 and 3, respectively,
Thus the difference between these two whole numbers is,
= 3 - 0 = 3.
To know more about percentage, visit,
https://brainly.com/question/26497520
#Percentage
Neil change the oil in his vehicle the car requires 6 quarts of oil if Neil wants to change his or every month for a year how many quarts of oil will Neil need?
Answers
Answer:
72 quarts
Step-by-step explanation:
1 year = 12 months, and Neil changes the oil each month, and each month he uses 6 quarts of oil. So, the number of quarts he will need for a year is
6 + 6 + ... + 6, twelve times, which equals 12(6) = 72 quarts.
3. Taylor has a $30.00 gift card that she can spend at the store. She has already bought a $9.00 picture frame, and she wants to buy $3.00 journals with the leftover money on the card. How many journals can she buy without going over the card's limit?
Variable:
Inequality:
Solution:
Answers
Answer:
She can buy 7 journals
$30.00-$9.00=$21.00
$3.00x7 journals=$21.00
, An Arithmetic Sequence
Term 1
Value 7
Explicit function mulle
63

Answers
The explicit rule is aₙ = 7+5(n-1), where n is the position of the term.
The complete table is given below.
What is the explicit rule for the arithmetic sequence?An explicit formula is a formula that allows us to find the nth term of an arithmetic sequence. Based on this formula, the sum of the arithmetic series can be derived.
The first term a₁=7 and the fourth term a₄=22.
The arithmetic explicit formula for the nth term is aₙ=a₁+(n-1)d, where d is a common difference.
So, find the value of d using a₁=7 and a₄=22 in the formula.
22=7+(4-1)d
15=3d
d=5
Therefore, the explicit formula becomes aₙ = 7+5(n-1).
Substitute n=2 and n=3 into the obtained formula.
a₂=7+5(2-1)
=7+5
=12
a₃=7+5(3-1)
=7+10
=17
Therefore, the required answers are a₂=12 and a₃=17.
To learn more about the explicit rule for arithmetic sequence visit this link
https://brainly.com/question/14864927
#SPJ9

What is 2 7/9 + 8/9 ?
Answers
Answer:
11/6
Step-by-step explanation:
2 7/9 + 8/9
2 7/9 into a mixed fraction which is 25/9
now 25/9 + 8/9 = 33/18 then simplify which is 11/6
Two groups of people, the Yellow Group and the Orange Group, suddenly find themselves in a world where there are only two 'production opportunities': pumping water and picking berries.
After a little while the Yellow Group has learned that it seems to produce about 2 gallons per hour while pumping water and about 8 berries per hour while picking.
Meanwhile the Orange Group has learned that it seems to produce about 1 gallon per hour while pumping water and about 3 berries per hour while picking.
If we were able to make production decisions that were efficient from the perspective of both groups combined, what would we consider to be the opportunity cost of producing one gallon of water?
3 berries
4 berries
25 cents
33⅓ cents
Answers
Answer:
3 berries
Explanation:
Opportunity costs for the Orange group:
Opportunity cost of pumping 1 gallon of water = 3/1 = 3 berries
Opportunity cost of picking 1 berry = 1/3 = 0.333 gallons of water
Opportunity costs for the Yellow group:
Opportunity cost of pumping 1 gallon of water = 8/2 = 4 berries
Opportunity cost of picking 1 berry = 2/8 = 0.25 gallons of water
Opportunity cost for both groups combined:
Opportunity cost of pumping 1 gallon of water = 3 berries (Orange group should pump water since opportunity cost is lower)
Opportunity cost of picking 1 berry = 0.25 gallons of water (Yellow group should pick berries since opportunity cost is lower)
Opportunity costs are the extra costs or benefits lost resulting from choosing one investment or activity over another alternative. In this case, people can either pump water or pick berries, but they cannot do both at the same time. When they are pumping water, the opportunity cost is the amount of berries that they will not be able to collect, and vice versa.
There are 600 cars in the parking lot. The ratio of red cars to white cars is 3:5. How many red cars and how many white cars are there in the parking lot?
Answers
Answer:
225 red cars & 375 white cars
Step-by-step explanation:
According to the specified ratio, there are 225 red cars and 375 white cars in the parking lot.
What is ratio?The ratio can be defined as the number that can be used to represent one quantity as a percentage of another. Only when the two numbers in a ratio have the same unit can they be compared. Ratios are used to compare two objects.
given, There are 600 cars in the parking lot. The ratio of red cars to white cars is 3:5. let ratio is in the term of variable x
Thus,
3x + 5x = 600
=> 8x = 600
=> x = 75
Total number of red cars = 3x
Total number of red cars = 3 * 75
Total number of red cars = 225
Total number of white cars = 5x
Total number of white cars = 5*75
Total number of white cars = 375
Therefore, there are 225 red cars and 375 white cars in the parking lot as per the given ratio.
Learn more about ratios here:
https://brainly.com/question/13419413
#SPJ2
Evaluate x^{3} - 3y when x = -3 and y = 4.
Answers
Answer:
-39
Step-by-step explanation:
Substitute x by - 3 and y by 4
(-3)^3 - 3 *4 = - 39
Which graph shows function f?

Answers
The graph of f(x) is the second one, so the correct option is B.
Which graph shows function f?Here we have f(x), a piecewise function, and we want to see which one of the four graphs is the correct one.
You can see that the first domain of the function is:
x ≤ -4
So we must have a closed circle at x = -4, when the parabola ends.
The second domain is:
-4 < x < 1
So x here is not equal to -4 nor 1, so this part starts and ends with open circles.
finally, the linear part starts with a closed circle.
Also, notice that the line has a negative slope, so it goes down, then we can discard the first option.
Then we can see that the correct option is the second graph.
Learn more about piecwise functions:
https://brainly.com/question/3628123
#SPJ1
help me plzzzzzzzzzzz
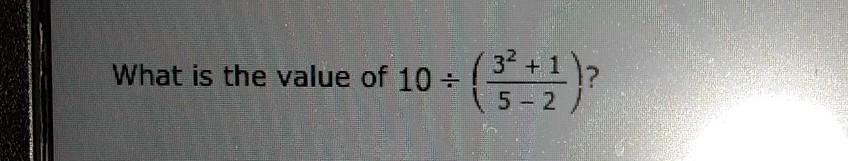
Answers
Answer:
\(3\)
Step-by-step explanation:
\(10 \div ( \frac{ {3}^{2} + 1 }{5 - 2} )\)
\( \frac{10(5 - 2)}{ {3}^{2} + 1} \)
\( \frac{10 \times 3}{ {3}^{2} + 1 } \)
\( \frac{30}{ {3}^{2} + 1 } \)
\( \frac{30}{9 + 1} \)
\( \frac{30}{10} \)
\(3\)
Find the value of x?

Answers
Answer:
x=25
All triangles must equal 180
95+35=130
The following sample was collected during registration at a large middle school. At the 0.05 level of significance, can it be concluded that level of math is dependent on grade level?
Honors Math Regular Math General Math
6th Grade 34 45 15
7th Grade 37 49 13
8th Grade 29 45 17
Hypotheses:
H0: Level of math is independent of/dependent on grade level.
H1: Level of math is independent of/dependent on grade level.
Enter the expected matrix - round to 4 decimal places.
Answers
Solution :
The expected matrix is :
\($E_i=\frac{(\text{row total } \times \text{column total})}{\text{grand total}}$\) Honors Regular General
6 th grade 33.0986 46.0070 14.8944
7 th grade 34.8592 48.4542 15.6866
8 th grade 32.0423 44.5387 14.4190
Thus we can say that the level of math is not dependent on the grade level.
Therefore, the provided information is correct. Test Stat = 1.4007, p-value = 0.844070419
\(H_0\) : The level of math is independent of the grade level.
\(H_1\) : The level of math is dependent on the grade level.
25 POINTS PLS HELP SOME1!!


Answers
The transformation from the graph of f(x) = x to the graph of g(x) = (1/9)·x -2, is a rotation and a translation. The correct option is therefore;
The transformation are a rotation and a translation
What is a translation transformation?A translation transformation is a transformation in which there is a displacement of all points on the preimage figure in a specified direction.
The transformation from f(x) = x to f(x) = (1/9)·x - 2, includes a slope reduction by a factor of (1/9), or rotating the graph of f(x) = x in the clockwise direction, and a translation of 2 units downwards, such that the y-intercept changes from 0 in the parent function, f(x) = x to -2 in the specified function f(x) = (1/9)·x - 2, therefore, the translation includes a rotation clockwise and a translation downwards by two units
The correct option is the second option; The transformation are a rotation and a translation
Learn more on rotation transformation here: https://brainly.com/question/29022349
#SPJ1
Which of the following random variables are discrete?
I. L= the number of pages in a randomly selected book
II. A = the number of leaves on a randomly selected tree
III. K= the height of a randomly selected NBA player
a. I only
I and II
b. II and III
c. II and III
d. l,ll, lll
Answers
Answer:
Step-by-step explanation:
I and II
Pages in a book and leaves on a tree can be counted precisely. They are discrete.
The height of a person cannot be measured exactly. We can get very good
approximations (to a lot of decimal places) but never exact. This is continuous.
Find the surface area
of the figure below:
19 cm
30 cm.

Answers
The surface area of the figure is approximately 997.5π cm².
We have,
The figure has two shapes:
Cone and a semicircle
Now,
The surface area of a cone:
= πr (r + l)
where r is the radius of the base and l is the slant height.
Given that
r = 15 cm and l = 19 cm, we can substitute these values into the formula:
= π(15)(15 + 19) = 885π cm² (rounded to the nearest whole number)
The surface area of a semicircle:
= (πr²) / 2
Given that r = 15 cm, we can substitute this value into the formula:
= (π(15)²) / 2
= 112.5π cm² (rounded to one decimal place)
The surface area of the figure:
To find the total surface area of the figure, we add the surface area of the cone and the surface area of the semicircle:
Now,
Total surface area
= 885π + 112.5π
= 997.5π cm² (rounded to one decimal place)
Therefore,
The surface area of the figure is approximately 997.5π cm².
Learn more about cones here:
https://brainly.com/question/13798146
#SPJ1
Evaluate the expression 8 –
5xy^3. for x = 3 and y = – 2.
A)278
B)-112
C)-72
D)128
Answers
Answer:
D) 128
Step-by-step explanation:
Because we will be replacing the variables with numbers we have to that we will have to do the exponent first because of PEMDAS.
\(8-5(3)(-2)^3\)
\(8-5(3)(-8)\)
\(8-15(-8)\)
\(8-(-120)\)
\(8+120=128\)
The sum of the ages of two brothers Kofi and Kwaku is 35. Kofi age is 2/3 of Kwaku's age. find their ages.
Answers
2/3 of 35 is 23. Kofi is 23.
Find the slope of the line that contains the points:
(-4, 3) and (4, 9)
a) 3/4
b) -3/4
c) 4/3
d) -4/3
Answers
Step-by-step explanation:
ATTACHED IS THE SOLUTION!!!
Answer:
The answer would be A. 3/4
Step-by-step explanation:
To find the slope, you divide the difference of the y-coordinates of 2 points on a line by the difference of the x-coordinates of those same 2 points.
Match the parent function name with the equation. Linear Quadratic Radical Absolute Value Rational Exponential Log Cubic Cube Root
Answers
Step-by-step explanation: The correct graph is #6. Cubic Function
The next model of a sports car will cost 14.7% more than the current model. The current model costs $34,000. How much will the price increase in dollars?
What will be the price of the next model?
Increase in price:
Price of next model:
Answers
Answer: $4,998
Step-by-step explanation:
34000*1.147
38998-34000=4998
Need help with some questions
https://kami.app/Cg5YfnU2L4ji
Answers
Answer:
Step-by-step explanation:
Thanks I will go there soon
m+q+ p; use m = 2, p = 1, and q = 3
Answers
2 + 1 + 3
3 + 3
6
Write v as the sum of two vector components if v = -5i+6j and w = 3i+4j
Answers
Vector v can be written as the sum of two vector components, \(v_x = -5i\) and \(v_y = 6j\)
To write vector v as the sum of two vector components, we need to decompose it into two vectors along different directions.
v = -5i + 6j
w = 3i + 4j
We can decompose vector v into two components, one along the x-axis and the other along the y-axis.
Let's denote the component along the x-axis as \(v_x\) and the component along the y-axis as \(v_y.\)
The x-component, \(v_x,\) represents the projection of vector v onto the x-axis and can be found using the dot product of v and the unit vector i:
\(v_x = v . i = (-5i + 6j) . i = -5i . i + 6j . i = -5\)
Similarly, the y-component, \(v_y,\) represents the projection of vector v onto the y-axis and can be found using the dot product of v and the unit vector j:
\(v_y = v . j = (-5i + 6j) . j = -5i . j + 6j . j = 6\)
Now, we can write vector v as the sum of its components:
\(v = v_x + v_y = -5i + 6j\)
So, vector v can be written as the sum of two vector components: -5i along the x-axis and 6j along the y-axis.
For similar question on components.
https://brainly.com/question/28351472
#SPJ11
i am a decimal number less than 1. the digit in my tenths place is an even prime number. my hundredths digit is twice my tenths digit, and my hundred thousandths digit is twice my hundredths digit. the thousandths digit is three less than my hundredths digit. my ten thousandths digit is the sum of my tenths and thousandths digit. what number am i?
Answers
Answer:
.
Step-by-step explanation:
Answer:
0.24857
Step-by-step explanation:
Less than 1 is 0. and
only even prime is 2
Suppose m<3=127 degrees. Find m<1.

Answers
Answer:
m∠1 = 37°
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASEquality PropertiesGeometry
Definition of a Line: A line is 180°All angles in a triangle add up to 180°Step-by-step explanation:
Step 1: Define
m∠3 = 127°
m∠G = 90°
Step 2: Find m∠2
Set up equation: m∠2 + 127 = 180Isolate unknown: m∠2 = 53°Step 3: Find m∠1
Set up equation: m∠1 + m∠2 + m∠G = 180Substitute: m∠1 + 53 + 90 = 180Combine like terms: m∠1 + 143 = 180Isolate unknown: m∠1 = 37°Translate and solve: 5 less than m is at most 70.
Write your solution in interval notation
Answers
The interval notation for the inequality statement "5 less than m is at most 70" is (-∞, 75].
What is an inequality?
In Algebra, an inequality is a mathematical statement that uses the inequality symbol to illustrate the relationship between two expressions. An inequality symbol has non-equal expressions on both sides. It indicates that the phrase on the left should be bigger or smaller than the expression on the right, or vice versa.
The statement given is - 5 less than m is at most 70.
The given sentence can be translated into a mathematical inequality as -
m - 5 ≤ 70
To solve for m, we can add 5 to both sides of the inequality -
m - 5 + 5 ≤ 70 + 5
m ≤ 75
Therefore, m is less than or equal to 75.
In interval notation, we can represent this solution as -
(-∞, 75]
Therefore, the interval value is (-∞, 75].
To learn more about inequality from the given link
https://brainly.com/question/11234618
#SPJ1
\( \binom{ \sin( \alpha) + \sin( 2alpha ) }{1 + \cos( \alpha ) + \cos(2 \alpha ) } = \tan( \alpha ) \)
Answers
I see you use the TeX command "\binom" for binomial coefficient, but I think you meant to use "\frac" to write a fraction, namely,
\(\dfrac{\sin(\alpha)+\sin(2\alpha)}{1+\cos(\alpha)+\cos(2\alpha)}=\tan(\alpha)\)
and I assume you're supposed to establish an identity.
Recall the double angle identities for cos and sin :
cos(2α) = cos²(α) - sin²(α) = 2 cos²(α) - 1
sin(2α) = 2 sin(α) cos(α)
Now expand the left side as
(sin(α) + sin(2α)) / (1 + cos(α) + cos(2α)) = (sin(α) + 2 sin(α) cos(α)) / (1 + cos(α) + 2 cos²(α) - 1)
Factor sin(α) from the numerator, and after canceling the 1s in the denominator and factor cos(α) :
… = [sin(α) (1 + 2 cos(α))] / [cos(α) (1 + 2 cos(α))]
Cancel the factors of 1 + 2 cos(α) :
… = sin(α) / cos(α)
which is equivalent to
… = tan(α)
by definition of tan.
What is 6y-3X=-18 written in slope-intercept form?
o y=-3x+3
O y=kx-3
O y=-2x+3
O y = 2x-3

Answers
Answer: B
Step-by-step explanation:
i need help on 6 I will provide I bigger picture

Answers
Looking at the diagram, there is a transversal cutting across 2 parallel lines.
Angle 2 and angle 6 lie in similar position on the same side of the transversal. This means that they are corresponding angles. Corresponding angles are equal.
Given that angle 2 = 32 degrees, then angle 6 = angle 2 = 32 degrees
angle 5 and angle 6 are linear pairs. They lie on a straight line. the sum of the angles on a straight line is 180 degrees. It means that
angle 5 + angle 6 = 180
angle 5 + 32 = 180
angle 5 = 180 - 32
angle 5 = 148 degrees
