Expand: y(0.5 +8)
Expand: 4(3+4x-2)
Answers
Answer:
.5y+8y=
8.5y
12+16x-8=
16x+4
Step-by-step explanation:
use the distributive property to solve the equation then simplify and combine like terms
Related Questions
Find det (A) given that A has p(A) as its characteristic polynomial. p(A) = 13 - 412 + +8 det (A) = i Hint: See the proof of Theorem 7.1.4. (lf given det (11 - A) = 1" + C21n-1 + ... + C, then, on setting A = 0, det (-A) = Cnor (- 1)"det (A) = Cn)
Answers
The determinant of matrix A, det(A), is equal to 8i.
To find the determinant of matrix A, we are given its characteristic polynomial p(A) = 13 - 412 + 8 det(A) = i. According to Theorem 7.1.4, if we set A = 0 in the polynomial p(A), we can obtain the determinant of -A.
Setting A = 0 in the polynomial p(A), we get p(0) = 13 - 412 + 8 det(0) = i. Simplifying this equation, we have 13 - 412 + 8 det(0) = i. Since det(0) is the determinant of a zero matrix, which is always zero, we can rewrite the equation as 13 - 412 = i. Solving for i, we find that i = -399.
Now, using the result from Theorem 7.1.4, we have det(-A) = C(-1)^n det(A). Plugging in the given value det(11 - A) = 1 + C21n-1 + ... + C, we can set A = 0 to find det(-A). By substituting A = 0 into the equation, we get det(11 - 0) = 1 + C21n-1 + ... + C, which simplifies to det(11) = 1 + C21n-1 + ... + C. Since det(11) is the determinant of matrix 11, which is just 11, we have 11 = 1 + C21n-1 + ... + C. Simplifying further, we get 10 = C21n-1 + ... + C.
Finally, we can substitute det(A) = 8i (from the given characteristic polynomial) into the equation det(-A) = C(-1)^n det(A). Since we found i = -399, we have det(-A) = C(-1)^n * 8 * -399 = -3192C(-1)^n.
In conclusion, the determinant of matrix A, det(A), is equal to 8i, which simplifies to -3192C(-1)^n.
Learn more about determinant
brainly.com/question/31755910
#SPJ11
Find all solutions of the equation 2cos3x=1 in the interval [0,π)
.
Trigonometric Equations:
The general solution for any cosine equation cosθ=cosα
the general solution is θ=2nπ+α. All we need to find out the values of α and substitute the values of n.
Answers
The slope indicates how steep the line is, while the y-intercept indicates where the line intersects the y-axis. We have to solve the equation in the interval [0,π)The general solution for any cosine equation $cosθ=cosα$the general solution is $θ=2nπ+α$. All we need to find out the values of α and substitute the values of n.
We know that cos value is positive in first and fourth quadrant.$\frac{\pi}{3}$ is the angle which is between $0$ and $\pi$ and whose cos is Thus the solutions will be: and
Thus, the solutions in the interval $[0,\pi)$ are $x=\frac{\pi}{9}, \frac{5\pi}{9}$.
Hence, the solutions are $\frac{\pi}{9},\frac{5\pi}{9}.$
The slope-intercept form of a linear equation in mathematics is an equation of the form y = mx + b, where m is the slope of the line and b is the y-intercept, which is the point at which the line meets the y-axis. The slope-intercept form is a handy approach to represent a line's equation because it allows you to quickly see the line and determine its slope and y-intercept. The slope indicates how steep the line is, while the y-intercept indicates where the line intersects the y-axis.
To know more about slope intercept visit:
https://brainly.com/question/19824331
#SPJ11
The Mountain States Office of State Farm Insurance Company reports that approximately 82% of all automobile damage liability claims were made by people under 25 years of age. A random sample of seven automobile insurance liability claims is under study. For samples of size 7, what is the expected number of claims made by people under 25 years of age
Answers
The expected number of claims made by people under 25 years of age is 5.74.
For this problem, we can use the binomial distribution which states that the probability of success (p) is equal to the proportion of people under 25 making claims (82%) and the probability of failure (q) is equal to the proportion of people over 25 making claims (1 - 82% = 18%).
The expected number of claims made by people under 25 is equal to the total sample size (7) times the proportion of people under 25 making claims (0.82) so the expected number of claims made by people under 25 is 7×0.82 = 5.74.
Hence, the expected number of claims made by people under 25 years of age is 5.74.
Learn more about the random sample here:
https://brainly.com/question/12719656.
#SPJ4
note: this is a multi-part question. once an answer is submitted, you will be unable to return to this part. a girl operates a radio-controlled model car in a vacant parking lot. the girl’s position is at the origin of the xy coordinate axes, and the surface of the parking lot lies in the x-y plane. she drives the car in a straight line so that the x coordinate is defined by the relation x(t)
Answers
At time t, the position is x(t) = 0.5t3 - 3t2 + 3t + 2.
What are coordinates?Coordinates are two numbers (Cartesian coordinates) or a letter and a number that point to a specific point on a grid known as a coordinate plane. A coordinate plane has four quadrants and two axes: x (horizontal) and y (vertical).To find the position:
The derivative of x with respect to t is zero when the velocity is zero. That is to say,
x' = 1.5t² - 6t + 3 = 0 or t² - 4t + 2 = 0Use the quadratic formula to solve.
t = (1/2) [ 4 +/- √(16 - 8)] = 3.4142 or 0.5858 sWhen t =0.5858 s, the position is:
x = 0.5(0.5858³) - 3(0.5858²) + 3(0.5858) + 2 = 2.828 mWhen t=3.4142 s, the position is:
x = 0.5(3.4142³) - 3(3.4142²) + 3(3.4142) + 2 = -2.828 mReject the negative answer.
So, when t = 0.586 s, the velocity is zero and the distance is 2.83 m.
The second derivative of x with respect to t is zero when the acceleration is zero.
That is to say,
3t - 6 = 0t = 2The distance traveled is:
x = 0.5(2³) - 3(2²) + 3(2) + 2 = 0So, when the acceleration is zero, t = 2 s, and the distance traveled is zero.
Therefore, at time t, the position is x(t) = 0.5t3 - 3t2 + 3t + 2.
Know more about coordinates here:
https://brainly.com/question/17206319
#SPJ4
The correct question is given below:
A girl operates a radio-controlled model car in a vacant parking lot. the girl’s position is at the origin of the XY coordinate axes, and the surface of the parking lot lies in the XY plane. she drives the car in a straight line so that the x coordinate is defined by the relation x(t) = 0.5t3 - 3t2 + 3t + 2 where x and t are expressed in meters and seconds, respectively. determine when the velocity is 0 m/s, and the position and the total distance traveled when the acceleration is zero.
The number of employees for a certain company has been decreasing each year by 5%. If the company cumently has 860 employees and this rate continues, find the number of employees in 10 years
The number of employees in 10 years will be approximately
(Round to the nearest whole number as needed)
Answers
Based on the exponential decay equation, the number of employees for the company that has been decreasing yearly by 5%, will in 10 years be approximately 515.
What is exponential decay equation?The exponential decay equation or function gives the value in t years that has a constant ratio of decrease.
Exponential decay equation is one of the two exponential functions. The other is the exponential growth equation.
The annual decrease in the number of employees = 5%
The current number of employees in the company = 860
The expected time = 10 years.
The exponential decay equation is as follows, y = 860 x 0.95^10.
y = 860 x 0.95^10 = 515
Learn more about exponential functions at https://brainly.com/question/30127596
#SPJ1
Find the slope of the line on the graph.
Write your answer as a fraction or a whole
number, not a mixed number or decimal.
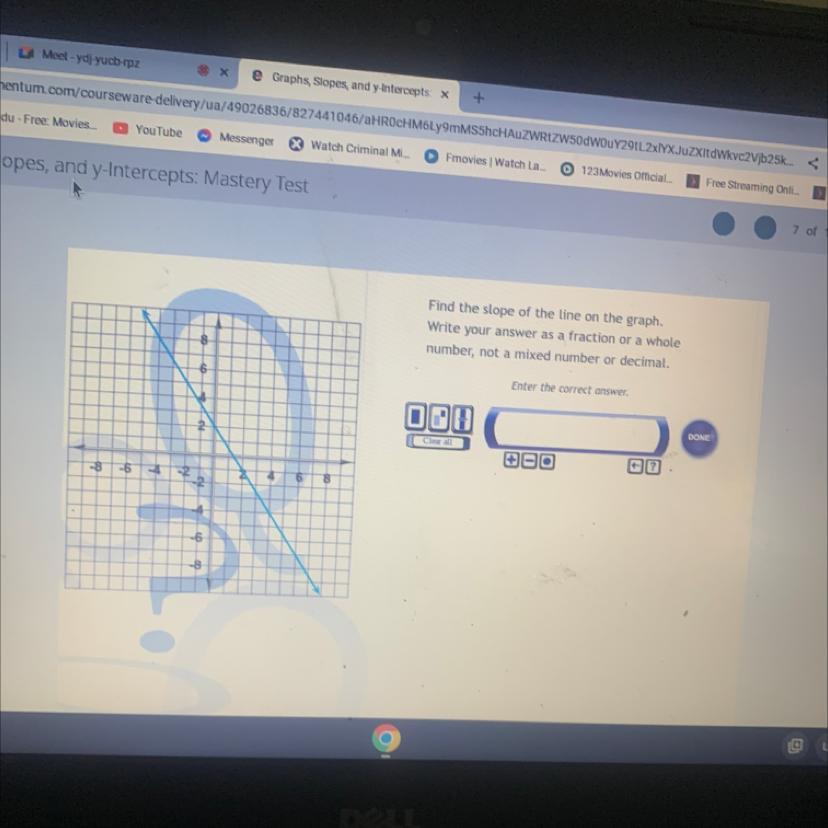
Answers
Answer:
3/2
Step-by-step explanation:
Write and equation of the line in slope-intercept form. (0,-2) (1,3)

Answers
Answer:
y=5x−2
I hope this helps!
an iterative version of a preorder traversal for a binary tree uses a(n)
Answers
An iterative version of a preorder traversal for a binary tree uses a stack.
Preorder traversal of a binary tree is a depth-first traversal algorithm that follows the order: root, left subtree, right subtree. In a recursive implementation, the function would first visit the root, then call itself recursively for the left subtree, and then call itself recursively for the right subtree.
In an iterative implementation, we use a stack to keep track of the nodes we need to visit. We push the root node onto the stack, and then while the stack is not empty, we pop a node from the stack and visit it. If the popped node has a right child, we push the right child onto the stack. If the popped node has a left child, we push the left child onto the stack. By doing so, we ensure that the nodes are visited in the correct order: root, left subtree, right subtree.
Using a stack instead of recursion can be more memory-efficient, since we are not storing all the recursive function calls on the call stack.
Learn more about traversal here
https://brainly.com/question/30000177
#SPJ11
What is an Integer
Answers
Answer:
A integer is number that can be written without a fractional or decimal component
Step-by-step explanation:
Answer:
An integer is a whole number. It doesn't matter whether it's positive or negative as long as its a whole number
(sorry if this doesn't make sense but I hope it helped)
The table shows the amount of money in Shawn's bank account as a
function of the number of weeks since school started.
Shawn's Bank Account
Number of Weeks Amount of Money
Answers
Answer:
400000000 dollar
Step-by-step explanation:
because why not
Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. (fg)(x) = nothing (Simplify your answer.) B. (fg)(x) does not exist. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. (fg)() nothing (Simplify your answer.) B. The value for (fg)() does not exist. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. (x) = nothing (Simplify your answer.) B. (x) does not exist. Click to select and enter your answer(s) and then click Check Answer.
Answers
Answer:
b
Step-by-step explanation:
Solve It! A search-and-rescue boat
spots a lost hiker on the edge of a
rock shelf. How many feet is the boat
from the hiker? Round to the nearest
whole foot and enter only a number.
Hint: Consider partitioning the
triangle into two right triangles.
Answers
Answer:
107
Step-by-step explanation:
Given
See attachment for boat and hiker
Required
The distance between the boat and the hiker
To do this, we make of sine rule.
\(\frac{a}{\sin A} = \frac{b}{\sin B} =\frac{c}{\sin C}\)
In this case:
\(x = ??\)
\(X = 68\)
\(a = 66\)
\(A = 35\)
So, we have:
\(\frac{x}{\sin 68} = \frac{66}{\sin 35}\)
Make x the subject
\(x = \frac{66}{\sin 35} * \sin 68\)
Using a calculator, we have:
\(x = \frac{66}{0.5736} * 0.9272\)
\(x = 115.063* 0.9272\)
\(x = 106.68\)
\(x \approx 107\)

order the measurements from greatest to least 45 inches, 6 yards, and 2 and1/4 feet
Answers
Answer:
2.25 feet, 45 inches, and 6 yards
Step-by-step explanation:
first, convert all to the same unit of measurement
I will use inches
45 inches = 45 inches
6 yards, 1 yard = 3 feet so 6 yards are equal to 18 feet and 1 foot is equal to 12 inches so 12*18 is 216 inches so 6 yards = 216 inches
Next 1 foot equals 12 inches so 2.25 * 12 = 27 so 2.25 feet = 27 inches.
Now let's look at the complete conversion
45 inches
6 yards = 216 inches
2.25 feet = 27 inches
looking at the inches we can see that 27 is the least then 45 then 216 therefore
2.25 feet < 45 inches < 6 yards so the order is
2.25 feet, 45 inches, and 6 yards
Which weighs less than 25 pounds 

Answers
Answer:
A. 400 ounces is 25lbs so yeah
Step-by-step explanation:
what will increase the width of a confidence interval? a) increase number in sample b) decrease confidence level. c) decrease variance d) increase variance.
Answers
The width of a confidence interval decreases as the sample size increases and increases as the confidence level increases.
What is a confidence interval?A confidence interval is a range of estimates for an unknown parameter in frequentist statistics. A confidence interval is calculated at a certain confidence level; the 95% confidence level is the most commonly used, although other levels, such as 90% or 99%, are also employed.So, we know that smaller samples result in narrower intervals.
With a higher sample size, we can more precisely estimate a population proportion.Therefore, a confidence interval narrows as the sample size grows and widens as the level of confidence rises.
learn more about confidence intervals here:
brainly.com/question/24131141
#SPJ4
A museum roomcircular in shape, has 5 equally spaced sensors on its walls. There are no dead or overlapping spots along the perimeter of the roomEach sensor has the same angle of detection What is the detection angle of each sensor ? Enter your answer in the box plsss help asap
Answers
Answer: 108 degrees.
Step-by-step explanation:
I think this is how you solve it:
A circle has a total of 360 degrees.
Having 5 equally placed sensors with a certain detection angle means that the sensors form a regular pentagon.
Finding the measure of the interior angles of a regular pentagon can be found using the formula
(180(n-2))/n, with n being the number of vertices of the polygon.
180(5-2)/5 ; 180(3)/5 ; 540/5 = 108
I think this means the detection angle is 108 degrees. Hope this helps!
If you get it wrong I'm terribly sorry T-T
The pentagons ABCDE and JKL MN are similar.
Find the length x of JK.
C
3
B
N
D
4
E
3
A
7
2.1
1.4
K
M
X
2.8
N
2.1
J

Answers
Answer:
3.5
Step-by-step explanation:
find the ratio between any two corresponding sides. for example : 1.4/2 = 0.7
this should be the same number for all sides
thus 5 * 0.7 = 3.5
Answer:
23456892245u
Step-by-step explanation:
Allah sh all will am am well ram chirac flow
Find the coordinates of the midpoint of a segment with the given endpoints.
V(-2,5), Z(3,-17)
Answers
The coordinate of the midpoint of the segment with the given endpoints is ( 1/2, -6 ).
What is the midpoint of the segment with the given endpoint?The midpoint formular used in finding the midpoint of a segment is expressed as;
( [x₁+x₂]/2 , [y₁+y₂]/2 )
Given the data in the question;
Point V(-2,5)
x₁ = -2y₁ = 5Point Z(3,-17)
x₂ = 3y₂ = -17Plug these values into the equation above.
( [x₁+x₂]/2 , [y₁+y₂]/2 )
( [(-2) + 3]/2 , [5 + (-17)]/2 )
( 1/2 , -12/2 )
( 1/2, -6 )
The coordinate of the midpoint of the segment with the given endpoints is ( 1/2, -6 ).
Learn more about the midpoint formular here: https://brainly.com/question/14687140
#SPJ1
The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b). True False
Answers
The statement "The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b)" is False.
In a uniform distribution, the probability density function (PDF) is constant within the interval [a, b]. The height of the PDF represents the density of the probability distribution at any given point within the interval. Since the PDF is constant, the height remains the same throughout the interval.
To determine the height of the PDF, we need to consider the interval length. In a uniform distribution defined on the interval [a, b], the height of the PDF is 1/(b - a) for the PDF to integrate to 1 over the entire interval. This means that the total area under the PDF curve is equal to 1, representing the total probability within the interval [a, b].
Therefore, the correct statement is that the height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is not 1/(a - b), but rather it is a constant value necessary for the PDF to integrate to 1 over the interval, i.e., 1/(b - a).
Learn more about uniform distribution here:
https://brainly.com/question/32291215
#SPJ11
the measure of an angle in standard position is given. find two positive angles and two negative angles that are coterminal with the given angle.
Answers
To find coterminal angles, you have to either add or subtract 2π. In this case, you would use 8π/4 so there is a common denominator.
Positives:
-3π/4+8π/4 = 5π/4
5π/4+8π/4 = 13π/4
Negative:
-3π/4-8π/4 = -11π/4
-11π/4-8π/4 = -19π/4
What is the measure of an angle?In geometry, an angle measure is the length of the angle formed by two rays or arms intersecting at a common vertex.
Using a protractor, angles are measured in degrees (°). Joseph Huddart created the protractor in 1801. It was a more sophisticated protractor.
The angle created at the center of a circle is measured in radians, the unit of angular measurement. It is described as an angle that subtends from a circle's center and intercepts at an arc with a radius equal to the circle's radius. 57.3° is equal to one radian.
Acute angle, Obtuse angle, Right angle, Straight angle, reflex angle, and full rotation are the names of basic angles.
To learn more about measure of an angle, visit:
https://brainly.com/question/14684647
#SPJ4
Find the distance (7,9) and (1,1) using the phythagorean theorem
Plsss I really need the answer
Answers
Answer:
Using the Pythagorean theorem we can first put the points into x and y
x1 = 7
y1 = 9
x2 = 1
y2 = 1
The distance between the two points can be found as follows:
d = √((x2 - x1)² + (y2 - y1)²)
= √((1 - 7)² + (1 - 9)²)
= √((-6)² + (-8)²)
= √(36 + 64)
= √100
= 10
Therefore, the distance between the points (7, 9) and (1, 1) is 10 units.
(4.2x10^6)(1.1x10^7)
Answers
Answer:4.62x10^13
Step-by-step explanation:
What are the solutions for the equation 2x^2+36=0.
A) x=+/- 6
B) x=+/- 6i
C) x=+/- 3 sqrt 2
D) x= +/- 3i sqrt 2
Answers
Answer:
the answer is x=+/- 3 sqrt 2
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11
In
1950
19501950, the per capita gross domestic product (GDP) of Australia was approximately
$
1800
$1800dollar sign, 1800. Each year afterwards, the per capita GDP increased by approximately
6.7
%
6.7%6, point, 7, percent.
Write a function that gives the approximate per capita GDP
G
(
t
)
G(t)G, left parenthesis, t, right parenthesis of Australia
t
tt years after
1950
19501950.
Do not enter commas in your answe
Answers
The function that approximates Australia's per capita GDP in t years after 1950 is \(G(t) =$1800(1.067)^t.\)
What is a Function?A function sets the value of one set's elements to the value of another set's specified element.
GDP represents the monetary worth of final products and services (those purchased by the final user) generated in a country over a certain time period.
According to the given information:
Given that Australia's GDP in 1950 was $1800, and that it is expanding by 6.7% per year, the GDP of Australia will increase by 6.7% each year after 1950.
As a result of the compounding effect, a function that gives the estimated per capita GDP of Australia in t years following 1950 can be expressed as follows:
\(GDP = 1800 + (1+6.7)^{t}\)
\(GDP = $1800 + (1+0.067)^t\)
\(GDP = $1800 + (1.067)^t\)
Hence, The function that approximates Australia's per capita GDP in t years after 1950 is \(G(t) =$1800(1.067)^t.\)
To know more about GDP, visit
brainly.com/question/15682765
#SPJ1
Inverse Function f(x)= -4 + 2/3x
Answers
Answer:
\(f^{-1}(x)=\frac{3x}{2} +6\)
Step-by-step explanation:
hope this helps
Urgent plz answer this

Answers
Answer: 2.75+ 3/4 = 3.5
Step-by-step explanation:
Answer:
1+1+3/4 is the correct answer, so in the first box put 1, and in the 2nd box put 1, and you'll be correct
What's 1+1 I will give brainliest
Answers
Answer:
2
Step-by-step explanation:
hope this helps :3
if it did pls mark brainliest
Answer:
2
Step-by-step explanation:
Numbers go in the order 1,2,3,4,5,6,7,8,9,10
If we go up one we will have two
Hope this helps
The measure of L in triangle LMN is 36°. The measure of M is 75°. What is the measure of N?
A.
111°
B.
39°
C.
69°
D.
249°
Answers
Answer:
C. 69°
Step-by-step explanation:
The sum of interior angles in a triangle is equal to 180
two of the angles are given to find the third one we subtract their sum from 180
180 - (36+75) = 69 degrees
Which inequality represents all values of x for which the product below is
defined?
x-5

Answers
Answer:
C. x ≥ 5
Step-by-step explanation:
You must meet both conditions:
(x -5) ≥ 0 and (x +2) ≥ 0
For the first condition, ...
x ≥ 5 . . . . add 5 to both sides
For the second condition ...
x ≥ -2 . . . . subtract 2 from both sides.
Since both conditions must be met, we must have ...
x ≥ 5