Exercises for Data Analytics Exercise Sheet-4 The fourth exercise is about linear regression. (4.1) Use "airquality" data set which provides air quality measurements in New York. (a) Identify variables which are strongly/weakly positively/negatively correlated. (b) Use t test and check if temperature is significantly different from 79. (c) Split the data into sample A with observations 1 to 77 and sample B with observations 78 to 153. Use t test and check if temperature is significantly different between samples A and B.
Answers
a) Variables strongly/weakly positively/negatively correlated in the "airquality" data set can be identified through correlation analysis.
b) The t-test can be used to check if the temperature variable in the "airquality" data set is significantly different from 79.
c) The t-test can be used to check if the temperature variable is significantly different between samples A and B (observations 1 to 77 and 78 to 153, respectively) in the "airquality" data set.
How to find the correlation analysis and t-tests applied to the "airquality" data set for variable identification and significance testing?a) To identify variables that are strongly/weakly positively/negatively correlated in the "airquality" data set, correlation analysis can be performed.
Correlation analysis measures the strength and direction of the linear relationship between variables.
By calculating correlation coefficients (such as Pearson's correlation coefficient), it is possible to determine if variables have a strong positive correlation (close to +1), weak positive correlation (between 0 and +1), strong negative correlation (close to -1), or weak negative correlation (between 0 and -1).
This analysis helps identify the nature of the relationships between variables in the dataset.
b) To check if the temperature variable in the "airquality" data set is significantly different from 79, a t-test can be conducted.
The t-test assesses whether the mean of a sample is significantly different from a hypothesized value (in this case, 79).
By comparing the t-statistic calculated from the sample data to the critical t-value at a given significance level, such as 0.05, it can be determined if the temperature is significantly different from 79.
If the calculated t-value falls outside the critical t-value range, the temperature variable is considered to be significantly different.
c) To check if the temperature variable is significantly different between samples A (observations 1 to 77) and B (observations 78 to 153) in the "airquality" data set, a t-test can also be used.
This comparison aims to determine if the means of temperature in samples A and B are significantly different.
By calculating the t-statistic and comparing it to the critical t-value at a chosen significance level, such as 0.05, it can be determined if the temperature variable differs significantly between the two samples.
If the calculated t-value falls outside the critical t-value range, it indicates a significant difference in temperature between samples A and B.
Learn more about correlation analysis
brainly.com/question/29785220
#SPJ11
Related Questions
Find the derivative of g'(x) = HINT: •4x [** 7x u + 4 u² +4 g(x) = du = 4x 7x 4x [** u +4 u² +4 u +4 - du u² + 4 -du + 0 u +4 -du +₁ u² + 4°
Answers
The derivative of g'(x) is 28x² + 8x + 4. This result is obtained by differentiating each term in the expression and simplifying the terms.
To find the derivative of g'(x), we differentiate the given expression term by term. The given expression is 4x * (7x + 4u + 4u² + 4g(x)). We can simplify this expression by distributing the 4x to each term inside the parentheses. This yields 28x² + 16xu + 16xu² + 16xg(x).
Next, we differentiate each term with respect to x. The derivative of 28x² with respect to x is 56x. The derivative of 16xu with respect to x is 16u, as the derivative of x with respect to x is 1. The derivative of 16xu² with respect to x is 32ux, using the power rule for differentiation. Finally, since g(x) is a function of x, we differentiate 16xg(x) using the product rule, which gives us 16g(x) + 16xg'(x), where g'(x) is the derivative of g(x) with respect to x.
Combining all the derivative terms, we obtain the derivative of g'(x) as 56x + 16u + 32ux + 16g(x) + 16xg'(x), which can be further simplified to 28x² + 8x + 4, as g'(x) does not depend on u and g'(x) represents the derivative of g(x).
In conclusion, the derivative of g'(x) is 28x² + 8x + 4.
Learn more about product rule here:
https://brainly.com/question/29198114
#SPJ11
You have
$
20
$20dollar sign, 20 to spend on taxi fare. The ride costs
$
5
$5dollar sign, 5 plus
$
2.50
$2.50dollar sign, 2, point, 50 per kilometer.
Write an inequality to determine the distance in kilometers,
�
dd, you can ride for
$
20
$20dollar sign, 20.
What is the maximum distance, in kilometers, you can ride for
$
20
?
$20?
Answers
After answering the given query, we can state that Since you have only equation $20, the inequality for the maximum distance "d" in kilometers would be: \(5 + 2.5d \leq 20\)
What is equation?In mathematics, the equals sign (=) is used to indicate equivalence and links two statements. The equality of two mathematical expressions is established by a mathematical statement used in algebraic equations. The equal sign, for instance, puts a space between the numbers 3x + 5 and 14 in the equation 3x + 5 = 14. You can use a mathematical expression to understand how the two lines that are written on the opposite edges of a letter relate to one another. The show's emblem is typically the same as the program's. One example is 2x - 4 = 2.
Let's assume the distance you can ride is "d" kilometers, then the cost of the ride would be:
5 + 2.5d
Since you have only $20, the inequality for the maximum distance "d" in kilometers would be:
\(5 + 2.5d \leq 20\)
Solving for "d", we get:
\(2.5d \leq 15\\d \leq 6\)
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Letf(x, y) = 2ex − y.Find the equation for the tangent plane to the graph of f at the point
Answers
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b. This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
To find the equation for the tangent plane to the graph of the function f(x, y) = 2e^x - y at a given point (x0, y0), we need to calculate the partial derivatives of f with respect to x and y at that point.
The partial derivative of f with respect to x, denoted as ∂f/∂x or fₓ, represents the rate of change of f with respect to x while keeping y constant. Similarly, the partial derivative of f with respect to y, denoted as ∂f/∂y or fᵧ, represents the rate of change of f with respect to y while keeping x constant.
Let's calculate these partial derivatives:
fₓ = d/dx(2e^x - y) = 2e^x
fᵧ = d/dy(2e^x - y) = -1
Now, we have the partial derivatives evaluated at the point (x0, y0). Let's assume our point of interest is (a, b), where a = x0 and b = y0.
At the point (a, b), the equation for the tangent plane is given by:
z - f(a, b) = fₓ(a, b)(x - a) + fᵧ(a, b)(y - b)
Substituting fₓ(a, b) = 2e^a and fᵧ(a, b) = -1, we have:
z - f(a, b) = 2e^a(x - a) - (y - b)
Now, let's substitute f(a, b) = 2e^a - b:
z - (2e^a - b) = 2e^a(x - a) - (y - b)
Rearranging and simplifying:
z = 2e^a(x - a) - (y - b) + 2e^a - b
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b.
This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
Learn more about tangent here:
https://brainly.com/question/10053881
#SPJ11
if we are testing for the difference between the mean of two independent populations with samples of n1=20 and n2=20 the number of degrees of freedom is qual to
Answers
df = [(s1^2/n1 + s2^2/n2)^2] / [((s1^2/n1)^2)/(n1 - 1) + ((s2^2/n2)^2)/(n2 - 1)]
where s1 and s2 are the sample standard deviations of the two populations.
Substituting the given values, we get:
df = [(s1^2/20 + s2^2/20)^2] / [((s1^2/20)^2)/19 + ((s2^2/20)^2)/19]
Since the values of s1 and s2 are not given, we cannot compute the value of df. However, in general, the degrees of freedom for a t-test with sample sizes of 20 and equal variances would be 38 (assuming a two-tailed test and a significance level of 0.05).
The polygons are similar. What is the value of x?

Answers
======================================================
Explanation:
The jump from CD = 2 to C'D' = 4 is "times 2". That must mean we go from BC = 3 to B'C' = 2*(BC) = 2*3 = 6. Therefore, x = 6.
-------
We could use a proportion to get the value of x as an alternative method:
(B'C')/(BC) = (C'D')/(CD)
x/3 = 4/2
2x = 3*4 ... cross multiply
2x = 12
x = 12/2 .... dividing both sides by 2
x = 6
Which expression represents the number 0.00074 in scientific notation?
Group of answer choices
Answers
Answer:
Answer: 7.4 x10^4 because you have to move the decimal to where the first number less then 10.
Step-by-step explanation:
Sophia has an ear infection. The doctor prescribes a course of antibiotics. Sophia is told to take 500 mg doses of the antibiotic regularly every 12 hours for 10 days. Sophia is curious and wants to know how much of the drug will be in her body over the course of the 10 days. She does some research online and finds out that at the end of 12 hours, about 4.5% of the drug is still in the body. What quantity of the drug is in the body right after the first dose, the second dose, the third dose, the fourth dose (10 points)? When will the total amount of the antibiotic in Sophia’s body be the highest? What is that amount (10 points)? Answer Sophia’s original question: Describe how much of the drug will be in her body at various points over the course of the 10 days (10 points).
Answers
Answer:
Dosage= 500 mg
Frequency= twice a day (every 12 hours)
Duration= 10 days
Number of dosage= 10*2= 20
residual drug amount after each dosage= 4.5%
We can build an equation to calculate residual drug amount:
d= 500*(4.5/100)*t= 22.5t, where d- is residual drug, t is number of dosageAfter first dose residual drug amount is: d= 500*0.045= 22.5 mg After second dose: d= 22.5*2= 45 mgAs per the equation, the higher the t, the greater the residual drug amount in the body.
Maximum drug will be in the body:
d= 20*22.5= 450 mg at the end of 10 daysMaximum drug will be in the body right after the last dose, when the amount will be:
500+19*22.5= 927.5 mgDescribe a sequence of transformations that shows that Polygon A is
congruent to Polygon B.
Answers
Answer:
25
Step-by-step explanation:
Consider the series ∑n=1[infinity]an where an=(5n−8)2n(3n 4)2n in this problem you must attempt to use the root test to decide whether the series converges
Answers
Applying the root test to the series ∑n=1[infinity]an, where an=(5n−8)2n(3n 4)2n, reveals that the series converges.
To determine the convergence of the series using the root test, we need to consider the limit of the absolute value of the nth root of the general term, as n approaches infinity. In this case, the general term is an=(5n−8)2n(3n 4)2n. Taking the nth root and absolute value, we have:
lim┬(n→∞)〖|an|^(1/n) 〗= lim┬(n→∞)〖|(5n−8)^(2n(3n 4)2n) 〗^(1/n) 〗
Simplifying the expression inside the limit:
|(5n−8)^(2n(3n 4)2n) 〗^(1/n) = |5n−8|^(2(3n 4)) = (5n−8)^(6n-8)
Now, as n approaches infinity, the base (5n−8) grows infinitely large, and since the exponent (6n-8) is also positive, the limit of the expression becomes infinity.
Therefore, lim┬(n→∞)〖|an|^(1/n) 〗= ∞.
Since the limit is greater than 1, according to the root test, the series ∑n=1[infinity]an diverges.
Learn more about root test here:
https://brainly.com/question/29461191
#SPJ11
Pls help me it’s overdue!!!

Answers
Answer:
Step-by-step explanation:
a = 1935 / 5 is the change
b = 1960 / 10 is the change
c = 1950 / 20 is the change
They are all increasing i'd assume they all went threw a positive change
1/5 divied by 2 as a fraction
Answers
The simplified form of the expression 1/5 divied by 2 as a fraction is 1/10.
What is 1/5 divied by 2 ?Given the expression in the question;
1/5 divied by 2
1/5 ÷ 2
To simplify, multiply 1/2 by the reciprocal of 2
1/5 ÷ 2
1/5 × 1/2
Simplify
( 1 × 1 ) / ( 5 × 2 )
( 1 ) / ( 5 × 2 )
Multiply 5 and 2
( 1 ) / ( 10 )
1/10
Therefore, the simplified form is 1/10.
Learn more about fractions heres; https://brainly.com/question/10354322
#SPJ1
Which is the graph of linear inequality 6x + 2y > –10?
On a coordinate plane, a dashed straight line with negative slope goes through (negative 2, 0) and (0, negative 6). Everything to the right of the line is shaded.
On a coordinate plane, a dashed straight line with negative slope goes through (0, 6) and (2, 0). Everything to the right of the line is shaded.
On a coordinate plane, a dashed straight line with positive slope goes through (0, negative 6) and (2, 0). Everything to the right of the line is shaded.
On a coordinate plane, a dashed straight line with positive slope goes through (negative 2, 0) and (0, 4). Everything to the right of the line is shaded.
Answers
Hope it helps :) and let me know if you want me to explain why
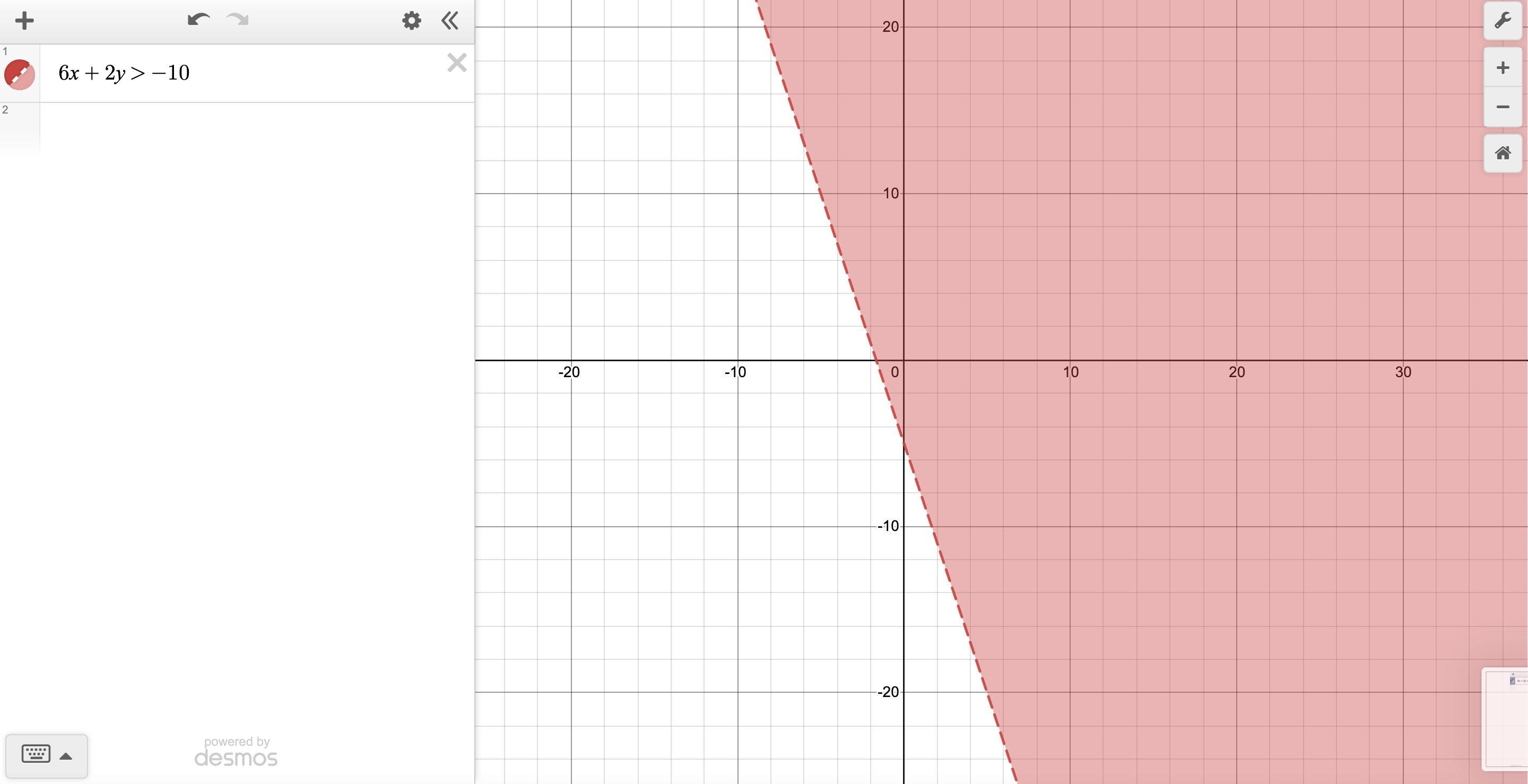
Answer:
A
Step-by-step explanation:
DECYPHERED
Which Line is Perpendicular to y= -1/4x - 8?
A) y=-4x+5
B) y=-1/4x-3
C) y=1/4x
D) y=4x+2
Answers
Answer:
D
Step-by-step explanation:
For two lines to be perpendicular, their gradients must have a product of -1The only one that fits this is DAnswer:
D
Step-by-step explanation:
The product of the slope of the perpendicular lines are -1
y = -1/4x - 8
Slope = -1/4
D) y = 4x + 2
Slope = 4
\(4 * \dfrac{-1}{4}=-1\)
Three professors at a university did an experiment to determine if economists are more selfish than other people. They dropped 64 stamped, addressed envelopes with $10 cash in different classrooms on the campus. 42% were returned overall. From the economics classes 58% of the envelopes were returned. From the business, psychology, and history classes 32% were returned. • R = money returned • E = economics classes • O = other classes1. ) Write a probability statement for the overall percent of money returned.
2. ) Write a probability statement for the percent of money returned out of the economics classes. 3. ) Write a probability statement for the percent of money returned out of the other classes.
Answers
According to the study, economists are not more self-centered than persons in other classes because 51% of the envelopes returned from economics classes and 36% from other classes.
What is meant by probability?Simply put, probability measures how probable something is to occur. We can discuss the probabilities of various outcomes, or how likely they are, whenever we are unsure of how an event will turn out. Statistics is the study of events subject to probability.
At one classroom for economics and another for other topics, they dumped 122 stamped envelopes with addresses and $20 bills inside each.
Let the money returned = R
economics classes = E
other classes = O
a). The following gives the probability statement for the overall percentage of the money returned: 100.P (R)
b). The probability statement that the percentage of money recovered from economics classes is 100.P(R|E)
c). The probability statement that displays the percentage of money returned from the other classes is 100.P(R|O).
d). No, because P(R) is not equal to P(R|E), the money returned is not independent of the classes.
e). According to the study, economists are not more self-centered than persons in other classes because 51% of the envelopes returned from economics classes and 36% from other classes.
The complete question is:
Three professors at George Washington University did an experiment to determine if economists are more selfish than other people. They dropped 122 stamped, addressed envelopes with $20 cash in two different classrooms (one economics, one not) on the George Washington campus. Of these, 42% were returned overall. From the economics class 51% of the envelopes were returned. From the other class 36% were returned.
From
the business, psychology, and history classes 31% were returned.
Let: R = money returned; E = economics classes; O = other classes
a. Write a probability statement for the overall percent of money returned.
b. Write a probability statement for the percent of money returned out of the economics classes.
c. Write a probability statement for the percent of money returned out of the other classes.
d. Is money being returned independent of the class? Justify your answer numerically and explain it.
e. Based upon this study, do you think that economists are more selfish than other people? Explain why or why not. Include numbers to justify your answer.
To learn more about probability refer to:
https://brainly.com/question/13604758
#SPJ1
the physical plant at the main campus of a large state university receives daily requests to replace fluorescent lightbulbs. the distribution of the number of daily requests is approximately normal and has a mean of 37 and a standard deviation of 10. use the empirical rule to determine the approximate proportion of lightbulb replacement requests numbering between 37 and 47? round your answer to four decimal places.
Answers
The approximate proportion of lightbulb replacement requests numbering between 37 and 47 can be determined using the empirical rule. The proportion is approximately 0.3413.
The empirical rule, also known as the 68-95-99.7 rule, states that for a normal distribution:
- Approximately 68% of the data falls within one standard deviation of the mean.
- Approximately 95% of the data falls within two standard deviations of the mean.
- Approximately 99.7% of the data falls within three standard deviations of the mean.
In this case, the mean is 37 and the standard deviation is 10. To find the proportion of lightbulb replacement requests between 37 and 47, we can use the empirical rule:
Proportion = P(37 ≤ X ≤ 47) ≈ P(mean - 1 standard deviation ≤ X ≤ mean + 1 standard deviation)
Proportion ≈ P(37 ≤ X ≤ 47) ≈ P(27 ≤ X ≤ 47)
Using the empirical rule, we know that approximately 68% of the data falls within one standard deviation of the mean. Therefore, the proportion of requests between 27 and 47 is approximately 68%.
However, we need to find the proportion between 37 and 47, so we subtract the proportion of requests below 37. Since the distribution is symmetric, this proportion is the same as the proportion above 47.
Proportion = 68% - (100% - 68%)
Proportion ≈ 0.68 - 0.32
Proportion ≈ 0.36
Rounding the proportion to four decimal places, we get approximately 0.3413.
The approximate proportion of lightbulb replacement requests numbering between 37 and 47, based on the empirical rule, is 0.3413. This means that around 34.13% of the daily requests fall within this range.
To know more about empirical rule, visit
https://brainly.com/question/30404590
#SPJ11
The following hypotheses were tested
H0: population mean= 0
Ha: population mean > 0
And a P value of 0.023 is obtained. What can be concluded?
a. the chance that the alternative hypothesis is true is 0.023
b. the chance that the null hypothesis is true is 0.023
c. the chance of obtaining a value of the test statistic as or more extreme than the value actually obtained if the null is true is 0.023
d. the chance of obtaining a value of the test statistic that is >0 is only 0.023 if the null is true
e. the chance that the null hypothesis is true is 0.977
Answers
We can conclude from the hypotheses that the chance of obtaining a value of the test statistic as or more extreme than the value actually obtained if the null is true is 0.023, option C.
On the premise that the null hypothesis is accurate, the p-value in null-hypothesis significance testing is the likelihood of generating test findings at least as severe as the result actually observed.
Given ,
The null and alternative hypothesis are respectivelly ,
H0: population mean= 0
Ha: population mean > 0
P value of this test is 0.023
We can conclude that,
the chance of obtaining a value of the test statistic as or more extreme than the value actually obtained if the null is true is 0.023
Option c is correct.
Learn more about Null Hypothesis:
https://brainly.com/question/25263462
#SPJ4
Find the seventh term of the geometric sequence from the given information. Express the term as an integer or simplified fraction.
a2 = -7 and r = 1/2
Answers
The seventh term of the geometric sequence is -7/32. The nth term of the sequence, a1 is the first term, r is the common ratio, and n is the position of the term
To find the seventh term of a geometric sequence, we can use the formula:
\(an = a1 * r^(n-1),\)
where an represents the nth term of the sequence, a1 is the first term, r is the common ratio, and n is the position of the term we want to find.
In this case, we are given a2 = -7 and r = 1/2.
Using the formula, we can find a1 by substituting n = 2:
a2 = a1 * (1/2)^(2-1).
We know that a2 = -7, so we can rewrite the equation:
-7 = a1 * (1/2)^1,
-7 = a1 * (1/2).
Now, let's solve for a1:
a1 = -7 * (2/1),
a1 = -14.
We have found that the first term, a1, is equal to -14.
Now, we can find the seventh term, a7, by substituting n = 7 into the formula:
a7 = (-14) * (1/2)^(7-1),
a7 = (-14) * (1/2)^6,
a7 = (-14) * (1/64),
a7 = -14/64,
a7 = -7/32.
Therefore, the seventh term of the geometric sequence is -7/32.
Learn more about geometric sequence here
https://brainly.com/question/1509142
#SPJ11
Naomi had a blast at the water park, even though she was 3 inches too short to ride the biggest slide, The Water Slinger. Naomi is 49 inches tall.
Let h represent the minimum height for The Water Slinger. Which equation models the problem?
Answers
This equation models the problem, where h represents the minimum height for The Water Slinger and Naomi is 49 inches tall. The inequality states that the difference between the minimum height and Naomi's height must be greater than or equal to 3 inches, meaning she is 3 inches too short to ride the slide.
10x + 3 = 8x + 3; x =
Answers
Answer:
x = 0
Step-by-step explanation:
Round 199.532 to the nearest tenth
Answers
Answer:
199.5
Step-by-step explanation:
3 is not greater than 5
Answer:
199.5
Step-by-step explanation:
The tenth place is the first number to the right of the decimal, in this case, it is 5. In order to know whether or not to raise it to 6 or keep it as 5, we have to look at the hundredth's value. If the number is 5 or higher, we change 5 to 6. If the number is 4 or lower, we keep the 5. In this case, the number is 3, which is 4 or lower. We keep the 5 as it is and get rid off all the numbers behind it. Resulting in:
199.5
What is the theoretical probability of rolling a 3 on a die?
Answers
Answer:
1/6 or 16.67% chance
Step-by-step explanation:
Assuming its a normal six sided dice. You would have a 16.67% chance of getting a 3.
what is the x-intercept of the graph 4x-6y=12
Answers
which of the trigonometric ratios has a value that is undefined?

Answers
Answer:
\(\tan \left(\frac{\pi }{2}\right)\)
Step-by-step explanation:
We know that tan(x) is defined as sin(x)/cos(x):
\(\tan \left(\frac{\pi }{2}\right),\\\sin \left(\frac{\pi }{2}\right)=1,\\\cos \left(\frac{\pi }{2}\right)=0,\\\\\)
\(\tan \left(\frac{\pi }{2}\right) = 1/0 \\\)
1/0 is undefined as 0 is in the denominator
PLEASE THERES 30 QUESTIONS AND IM ON 4 AND ITS DUE SOON i can only answer one q at a time omg. RKEGEB

Answers
Answer:
3 gallons.
Step-by-step explanation:
there are 3 gallons in 48 cups. apologies if i am wrong
!!20 POINTS!!
A gas pump measures the amount of gas pumped to the nearest 0.01 gallon.
Which measurement shows an appropriate level of precision for the pump?

Answers
Answer:
It's A. 11.12 gallons. I'm sure
Step-by-step explanation:
When we are computing a simple linear regression line, there are certain conditions that must be met for this model to be valid. One of these conditions is the equal spread condition. Which of these answers best explains how we check to make sure that this condition is met? a. Make sure there is similar spread around the sample mean of x. b. Make sure there is similar spread around the line at each value of x.
c. Make sure that there is similar spread around the sample mean of y. d. Make sure all outliers are only below the line.
Answers
The answers that best explains how we check to make sure that this condition is met is: c. Make sure there is similar spread around the sample mean of y.
How we check to make sure that this condition is met?The equal spread condition states that the residuals (differences between the actual and predicted values of y) should have roughly equal variance at each value of x.
To check if this condition is met, we examine the residual plot, which is a scatterplot of the residuals versus the independent variable x. If the spread of residuals around the mean is roughly equal for all x, then the equal spread condition is satisfied.
Therefore the correct option is C.
Learn more about actual and predicted values here:https://brainly.com/question/28610444
#SPJ1
Expand and simplify . 4a(2+3b)-5b(4a-10). PLEASE HELP. BEST ANSWER RECEIVES A BRIANLIEST
Answers
Answer:
12a+62b
Step-by-step explanation:
4a(2+3b)-5b(4a-10)
opening brackets
=8a+12b-20a+50b
=8a-20a+12b+50b
=-12a+62b
expand_and_simplify
(
4
⋅
a
⋅
(
2
+
3
⋅
b
)
-
5
⋅
b
⋅
(
4
⋅
a
-
10
)
.
)
=−5⋅b⋅(4⋅−10).+8⋅+12⋅⋅
=
-
5
⋅
b
⋅
(
4
⋅
a
-
10
)
.
+
8
⋅
a
+
12
⋅
a
⋅
b
4x+4= 12 what is x nccncmcndndnsjs
Answers
Answer:
x = 2
Step-by-step explanation:
4x+4 = 12
Subtract 4 on both sides:
4x = 8
Divide by 4 on both sides:
x = 2
Answer:
x = 2
Step-by-step explanation:
Hi there !
4x + 4 = 12
4x = 12 - 4
4x = 8
4x = 8 : 4
x = 2
Good luck !
\log _(5)(X+7)+\log _(5)(x+3)=1
Rewrite the given equation without logarithms. Do not solve for x.
Answers
The equation without logarithms is (X+7)(x+3) = 5.
\(\log_{b}M\) = n; M = \(b^n\) is used in equations that have logarithms on one side.
Here are the steps to answer this type of equation:
1. By using the proper laws of logarithms, simplify the logarithmic equations.
2. Convert the linear equation to an exponential form.
3. Next, reduce the exponent and find the variable.
4. Re-insert your solution into the logarithmic equation to validate it. You should be aware that a logarithmic equation can only ever provide a positive argument as its correct solution.
The equation is:
log₅(X+7) + log₅(x+3) = 1
We write the equation as
log₅(X+7)(x+3) = 1
Now the equation is:
(X+7)(x+3) = 5¹
(X+7)(x+3) = 5
To learn more about logarithms link is here
brainly.com/question/30085872
#SPJ4
The first two steps in determining the solution set of the system of equations, y = x2 – 6x + 12 and y = 2x – 4, algebraically are shown in the table.
Which represents the solution(s) of this system of equations?
(4, 4)
(–4, –12)
(4, 4) and (–4, 12)
(–4, 4) and (4, 12)

Answers
Answer:
(4,4)
Step-by-step explanation:
The solution set of the system of equations can be found by setting the two equations equal to each other and solving for x.
x^2 - 6x + 12 = 2x - 4
x^2 - 8x + 16 = 0
(x - 4)^2 = 0
x = 4
Since both equations in the system are equal to y, we can substitute x = 4 into either equation to find the corresponding value of y.
y = 2x - 4 = 2(4) - 4 = 4
Therefore, the solution of this system of equations is (4, 4).
Therefore, the correct answer is (4, 4).