Estimate 407,001 -184,652
Answers
Answer:
\copy n paste your answer and it should be there
Step-by-step explanation:
Related Questions
What is the solution of the equation 3 and minus 2 is equal to 46?
Answers
The solution of the equation 3z minus 2 is equal to 46 is 16.
The given equation '3z minus 2 is equal to 46' can be written as
3z - 2 = 46
Now solving for z because the value of z will give the required solution of the given equation. So now finding the z from the equation:
3z = 46 + 2
3z = 48
z = 48/3
z = 16
The value of the z is 16 which represents the solution of the given equation i.e 3z minus 2 is equal to 46.
Therefore it is concluded that the solution of the equation 3z minus 2 is equal to 46 is 16.
You can learn more about equation at
https://brainly.com/question/22688504
#SPJ4
currently allowed by drones is 400 feet, which is approximately 0.12 km. This is to ensure that drones do not interfere with other aircraft or cause safety hazards. If cameras in a drone are set to film toward the horizon, what is the greatest distance that can be filmed, given that the radius of the Earth is approximately 6358 km?
Answers
6358.023 km is the greatest distance that can be filmed, given that the radius of the Earth is approximately 6358 km.
To find the greatest distance that can be filmed when the cameras in a drone are set to film toward the horizon, we need to consider the curvature of the Earth.
When a drone is flying at the maximum allowed altitude of 400 feet (approximately 0.12 km), the line of sight from the drone's cameras will form a tangent to the Earth's surface. We can consider this tangent line as forming a right triangle with the Earth's radius (6358 km) as the hypotenuse.
Using the Pythagorean theorem, we can calculate the distance from the drone to the horizon as follows:
distance to horizon = \(√(radius^{2} + altitude^{2})\)
distance to horizon = \(√((6358 Km)^{2} + (0.12 Km^{2}))\)
distance to horizon ≈ \(√((40405664 Km)^{2} + (0.144 Km^{2}))\)
distance to horizon ≈ \(√40405664.0144 Km^{2}\)
distance to horizon ≈ 6358.023 km
Therefore, the greatest distance that can be filmed when the cameras in the drone are set to film toward the horizon is approximately 6358.023 km.
Know more about Pythagorean theorem here:
https://brainly.com/question/343682
#SPJ8
Katie wants to hang a painting in a gallery. The painting and frame must have an area of 45 square feet. The painting is 6 feet wide by 7 feet long. Which quadratic equation can be used to determine the thickness of the frame, x?
4x2 + 26x + 45 = 0
4x2 + 26x − 3 = 0
x2 + 13x − 3 = 0
x2 + 13x + 45 = 0
Answers
Answer:
4x² + 26x - 3 = 0
Step-by-step explanation:
We assume the width of the frame is the same along all sides and is x.
The length of the painting plus the frame is 7 + 2x, or 2x + 7.
The width of the painting plus the frame is 6 + 2x, or 2x + 6.
(2x + 7)(2x + 6) = 45
4x² + 12x + 14x + 42 = 45
4x² + 26x - 3 = 0
Some number added to -11 is 37. Divide this number by -12. Then, multiply by -8. What is the final number?
Answers
The value of the final number with the given steps and operations is 32
Calculating the value of the final number?Given that
Some number added to -11 is 37. Divide this number by -12. Then, multiply by -8.Represent the number with x
So, we have
x - 11 = 37
Add 11 to both sides
So, we have
x = 48
Divide by -12
We get
x/-12 = -4
Multily by -8
-8x/-12 = 32
hence, the final number is 32
Read more about expression at
https://brainly.com/question/1859113
#SPJ1
Type the correct answer in the box. express your answer to two significant figures. a reaction between 1.7 moles of zinc iodide and excess sodium carbonate yields 12.6 grams of zinc carbonate. this is the equation for the reaction: na2co3 zni2 → 2nai znco3. what is the percent yield of zinc carbonate? the percent yield of zinc carbonate is %.
Answers
The percent yield of zinc carbonate is 5.91%.
What is chemical reaction?The chemical reaction is the reaction between two reactants which led to the formation of products.
The products are substances which forms after reaction. The reactants are the substances which are original materials.
Given is a reaction between 1.7 moles of zinc iodide and excess sodium carbonate yields 12.6 grams of zinc carbonate.
The given balanced equation is: Na₂CO₃ + ZnI₂ → 2NaI + ZnCO₃
From given moles of zinc iodide, the moles of zinc carbonate
1.7 moles of ZnI₂ = 1.7 moles of ZnCO₃
Molar mass of zinc carbonate is 125.38 g/mol
Theoretical yield = 1.7 moles of ZnCO₃ x 125.38 g/mol = 213.15 g ZnCO₃
Theoretical yield is 213.15 g and the actual yield is given as 12.6 g.
percent yield = [ 12.6 g / 213.15 g ZnCO₃ ] x 100
percent yield = 5.91%
The percent yield of zinc carbonate is 5.91%.
Learn more about chemical reaction.
https://brainly.com/question/22817140
#SPJ1
Find h(7) - 3 if h(x) = 5x^2 + 11
Answers
Answer:
\(h(7) - 3 = \: 5 {(7)}^{2} + 11 - 3 \\ = 5(49) + 8\)
answer: the answer is 253
two balls are picked at random from a box containing 3 red balls and 3 green balls. what is the probability that 1 red ball abd 1 green ball is selected?
o 4/13
o 15/28
o answer is not given in the choices
o 3/5
o 5/10
o 9/28
Answers
Answer: 5/10
Step-by-step explanation:
because there is three balls each and you could pick either a red one or a green one
Convex quadrilateral ABCD is given: Lines AB and C Dintersect in point T.WfAT = 3 units, TD 6 units, TC 10 units, and 0 +1=8+6 = 180" the length of the line segment' AB is: A 13 units B 15 units C 17 units
Answers
The length of the line segment AB is 4.8 units
To find the length of the line segment AB in the convex quadrilateral ABCD with given information, we can use the following steps:
Step 1: Identify the given information
We are given that \(AT = 3 units\) , \(TD = 6 units,\) \(TC=10 units\) and angle sum is 180 degrees.
Step 2: Utilize the Angle Bisector Theorem
Since lines AB and CD intersect in point T, we can apply the Angle Bisector Theorem to triangle ATC, with TD being the angle bisector. The theorem states that the ratio of the lengths of AT to TB is equal to the ratio of the lengths of CT to TD:
\(\frac{AT}{TB} = \frac{CT}{TD}\)
Step 3: Plug in the given values and solve for TB
Using the given values, we can set up the equation:
\(\frac{3}{TB} = \frac{10}{6}\)
To solve for TB, we can cross-multiply:
\(3(6)=10(TB)\\18=10(TB)\)
Now, divide both sides by 10:
Step 4: Find the length of line segment AB
To find the length of AB, we simply add the lengths of AT and TB:
\(AB = AT + TB\)
\(AB = 3 + 1.8\)
\(AB = 4.8 units\)
So, the length of the line segment AB is 4.8 units.
To know more about "Angle Bisector Theorem" refer here:
https://brainly.com/question/28565813#
#SPJ11
What is the perimeter of the quadrilateral JKML? Show complete work.

Answers
Answer:13cm
Step-by-step explanation:
What is the value of x to the nearest degree?
22
63
77
68

Answers
Answer:
I need help on this to anyone please
The length of a rectangle is 3 more than twice its width. If the
perimeter of the rectangle can be no more than 78 ft, what are all of
the possible widths of
the rectangle?
.
Answers
Answer:
x <= 9.75
Step-by-step explanation:
W = x
L = 3x
P = 2L + 2W <= 78
2(3x) + 2(x) <= 78
6x + 2x <= 78
8x <= 78
x <= 9.75
I need this by tomorrow 3.

Answers
Answer:
it's the first one girl! :)
Step-by-step explanation:
Answer:
That is correct at least to what know...
Step-by-step explanation:
in a probability-proportional-to-size sample with a sampling interval of $5,000, an auditor discovered that a selected account receivable with a recorded amount of $10,000 has an audit amount of $8,000. if this were the only error discovered by the auditor, the projected error of this sample would be group of answer choices a. $2,000 understatement. b. $2,000 overstatement. c. $5,000 understatement. d. $5,000 overstatement.
Answers
The projected error of this sample would be an understatement of $2,000.
Hence, the correct option is A.
Step 1. In a probability-proportional-to-size sample, the projected error can be determined by calculating the difference between the recorded amount and the audit amount, and then scaling it up to the population using the sampling interval.
Step 2. Given:
Sampling interval = $5,000
Recorded amount = $10,000
Audit amount = $8,000
Step 3. Projected error = (Audit amount - Recorded amount) * (Population size / Sample size)
Step 4. In this case, since it is mentioned that this is the only error discovered by the auditor, the sample size can be assumed to be 1.
Projected error = ($8,000 - $10,000) * (Population size / 1)
Step 5. Since the error is the difference between the recorded amount and the audit amount, and the audit amount is lower than the recorded amount, it indicates an understatement.
Therefore, the projected error of this sample would be an understatement of $2,000.
Hence, the correct option is A.
To know more about error here
https://brainly.com/question/31795694
#SPJ4
Use the diagram to find the height of statue.round to the nearest tenth

Answers
Answer:
7.3 ft
Step-by-step explanation:
The information given represents a right angle triangle with the following:
reference angle = 52°
Adjacent side length = 5.7 ft.
Opposite side length = height of the statue = h
Applying the trigonometric ratio formula, we would have:
\( tan(52) = \frac{h}{5.7} \)
Multiply both sides by 5.7
\( tan(52) \times 5.7 = \frac{h}{5.7} \times 5.7 \)
\( tan(52) \times 5.7 = h \)
\( h = 7.3 ft \) (nearest tenth)
Look at pic and see if u can help me. Need it broken down

Answers
How I got this answer is I found a relation in 21 and 7, 7 is the product of dividing 21 by 3
Using that you take the 6 in the first parallelogram and divide that by 3 and you get 2.

Given 4 < x < 9 and 5 - y< 4 , where x and y are integers. Find the maximum value of x-y.
Answers
Answer:
You want to maximize x and minimize y
Maximum y = 8
Minimum y = 10
8-10= -2
Samuel worked at a beach stand over the summer. He worked 6 hours a day 4 days a week. He earned $7.50 per hour how much money did he make in one week?
Answers
Step-by-step explanation:
Earning per hour for Samuel = $7.50
No. of hours worked in a day = 6
Earning for a day = Earning per hour for Samuel *No. of hours worked in a day
Earning for a day = $7.50 *6 = $45
___________________________________________________
No of days worked in a week by Samuel = 4
Earning for week = Earning for a day *No of days worked in a week by Samuel
Earning for week = $45*4 = $180
_____________________________________________________
No. of weeks worked in summer = 8
Total earning in the summer = Earning for week *No. of weeks worked in summer
Total earning in the summer = $180*8 = $1440 (Answer)
*NOT MY ANSWER SOMEONE ALREADY ANSWERED THIS***
SHOW WORK AND I WILL GIVE BRAINIEST!!!
Lisa is making some spiced tea for her mom. The recipe calls for 2.5 cups of sugar for each cup of tea. If she only uses 3/4 cups of tea, how much sugar should she use?
Answers
Answer:
1.875 cups of sugar
Step-by-step explanation:
Find what 3/4 of 2.5 is
2.5 x 0.75 = 1.875 cups of sugar
An experiment consists of dealing 5 cards from a standard 52-card deck. What is the probability of being dealt a 3, 4, 5, 6, 7, all in the same suit? The probability of being dealt a 3, 4, 5,6, 7, all in the same suit is Round to seven decimal places as needed.)
Answers
The probability of being dealt a 3, 4, 5, 6, 7, all in the same suit is approximately 0.0000031.
To calculate the probability of being dealt a 3, 4, 5, 6, 7, all in the same suit, we can use the following formula:
P = (number of favorable outcomes) / (total number of possible outcomes)
the order in which the cards are chosen does not matter, so we need to divide by the number of ways we can arrange 5 cards, which is 5! (5 factorial).
Therefore, the total number of possible outcomes is (52 * 51 * 50 * 49 * 48) / (5 * 4 * 3 * 2 * 1), which simplifies to 2,598,960.
Finally, we can calculate the probability of being dealt a 3, 4, 5, 6, 7, all in the same suit:
P = 8 / 2,598,960
P = 0.00000308 (rounded to seven decimal places)
To know more about Probability:
https://brainly.com/question/30034780
#SPJ4
Graph f(x)=-2x+4. What is x when f(x) =-8
Answers
Answer:
-6
Step-by-step explanation:
-8=-2x+4 -8-4=2x -12=2x x= -12:2 x= -6
PLEASE HELP ME IM BEING TIMED

Answers
The domain of the function is defined as 0 ≤ x ≤ 4.
option A is the correct answer.
What is the domain of a function?A domain of a function refers to "all the values" that can go into a function without resulting in undefined values.
So the domain of a function is the set of x values, while the range of a function is the set of y values.
From the given statement, the range of the function is defined as;
y = vt
where;
v is the speedt is the time of motiony = 60 mph x 4 hr
y = 240 miles
From the given statement, the domain of the function is defined as;
0 ≤ x ≤ 4
Learn more about domain of function here: https://brainly.com/question/28934802
#SPJ1
question 2.
the center of a circle is located at (5,2) and a point in the circle is (-3,4) what is the radius of the circle?

Answers
Answer:
ss
Step-by-step explanation:
sas
The radius of the circle who center is at ( 5 , 2 ) and the point on the circle is ( -3 , 4 ) is given by r = 2√17 units
What is a Circle?A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “center”. Every line that passes through the circle forms the line of reflection symmetry. Also, the circle has rotational symmetry around the center for every angle
The circumference of circle = 2πr
The area of the circle = πr²
where r is the radius of the circle
The standard form of a circle is
( x - h )² + ( y - k )² = r²,
where r is the radius of the circle and (h,k) is the center of the circle.
The equation of circle is ( x - h )² + ( y - k )² = r²
For a unit circle , the radius r = 1
x² + y² = r² be equation (1)
Now , for a unit circle , the terminal side of angle θ is ( cos θ , sin θ )
Given data ,
Let the radius of the circle be r
Let the center of the circle be A ( 5 , 2 )
Let the point on the circle be P ( -3 , 4 )
Now , standard form of a circle is
( x - h )² + ( y - k )² = r²
So , r² = ( 5 - ( -3 ) )² + ( 2 - 4 )²
On simplifying the equation , we get
r² = ( 8 )² + ( 2 )²
r² = 64 + 4
r² = 68
Taking square roots on both sides , we get
r = √68
r = 2√17
Hence , the radius of the circle is 2√17 units
To learn more about circle click :
https://brainly.com/question/28391204
#SPJ2
The length of the base of a right triangle is twice the height. If the height is ten meters, find the area of the right triangle. A 20m2 B 60m2. C 100m2. D 200m2
Answers
Answer:
Area = 100m²
Step-by-step explanation:
Given :
Height of triangle = 10 m
Length of base = 2 * height = 2 * 10 = 20 m
Area of right angle triangle :
1/2 * base * height
Area = 1/2 * 20 * 10
Area = 0.5 * 10 * 20
Area = 100m²
36 POINTS! PLEASE HELP!!!! PLS-
Use ⊙N with KL≅JM.
What is JM?
a) 17
b) 30
C) 15
d) 8
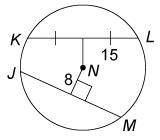
Answers
Answer:
you correct answer should be 17
Gretchen made a paper cone to hold a gift for a friend. The paper cone was 10 inches high and had a radius of 3 inches. Find the volume of the paper cone to the nearest tenth. Use 3.14 for π.
Answers
Answer:
139.9 \(in^3\)
Step-by-step explanation
here r=3 in, h =15 in
Volime =(1/3)x3.14x9x15=139.9 \(in^3\)
hope this helps :)
5a) Determine the measure of each unknown angle

Answers
Answer:
Step-by-step explanation:
25, i think
5. Prolific uses the bike in his trunk to find a nearby gas station with a mechanic to fix his rental
car. He rides 1.5 mi to the first gas station, where they say the next gas station may have a
mechanic. He then rides 1.6 mi to the next gas station, which also has no mechanic. The
following gas stations at 1.8 mi, 2.1 mi, and 2.5 mi away all have no mechanics available, but
confirm that there is a mechanic at the following gas station.
A. Assuming the rate remains constant, what equation will determine the distance of
the N gas station?
B.
If the pattern continues, how many miles will Prolific bike to get to the mechanic at
the 6th gas station?
Answers
Prolific will bike 2 miles to get to the mechanic at the 6th gas station if the pattern continues.
Assuming the rate remains constant, we can use the equation d = rt, where d is the distance, r is the rate, and t is the time. In this case, we want to find the equation to determine the distance of the Nth gas station.
Let's analyze the given information:
The first gas station is 1.5 miles away.
From the second gas station onwards, each gas station is located at a distance 0.1 miles greater than the previous one.
Based on this pattern, we can write the equation for the distance of the Nth gas station as follows:
d = 1.5 + 0.1(N - 1)
B. To find the distance Prolific will bike to get to the 6th gas station, we can substitute N = 6 into the equation from part A:
d = 1.5 + 0.1(6 - 1)
= 1.5 + 0.1(5)
= 1.5 + 0.5
= 2 miles
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
I will name brainliest :)

Answers
Answer:
The median and IQR
Step-by-step explanation:
Hope it helps
Using Interval Notation, state the Domain of any quadratic function, and explain in your own words why we know this to be true.
Answers
The domain of any quadratic function is all real numbers (-∞, ∞) because the quadratic function's graph is a smooth curve that extends indefinitely in both directions.
Any quadratic function takes the form f(x) = ax² + bx + c, where a, b, and c are real numbers and a ≠ 0.
By convention, the domain of a quadratic function is always all real numbers, which can be expressed using interval notation as (-∞, ∞).
This is because any real number can be inputted into a quadratic function and result in a real number output.
In other words, the domain of a quadratic function is the set of all real numbers for which the function is defined.
Therefore, we can say that the domain of any quadratic function is all real numbers (-∞, ∞) because the quadratic function's graph is a smooth curve that extends indefinitely in both directions.
The graph of a quadratic function has a parabolic shape that opens either upwards or downwards, depending on the sign of the leading coefficient a.
The domain of a quadratic function is essential for determining the range of the function.
For more questions on quadratic function
https://brainly.com/question/1214333
#SPJ8
518. Coin Change 2
You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.
Answers
If we have coins = [1, 2, 5] and amount = 5, then the function should return 4, because there are four combinations of coins that make up an amount of 5: [1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 2, 2], and [5].
This problem can be solved using dynamic programming. Let's define dp[i][j] as the number of combinations of coins using the first i coins to make up an amount j. Then we can use the following recurrence relation:
dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]
The first term on the right-hand side of the equation corresponds to the case where we don't use the i-th coin, while the second term corresponds to the case where we use the i-th coin at least once. Note that we only need to consider cases where j >= coins[i], because it's impossible to make up an amount less than the value of the i-th coin using that coin.
We can initialize dp[0][0] = 1, because there is exactly one way to make up an amount of zero using no coins. Finally, the answer to the problem is dp[n][amount], where n is the total number of coins.
Here's the Python code:
def change(amount, coins):
n = len(coins)
dp = [[0] * (amount+1) for _ in range(n+1)]
dp[0][0] = 1
for i in range(1, n+1):
dp[i][0] = 1
for j in range(1, amount+1):
dp[i][j] = dp[i-1][j]
if j >= coins[i-1]:
dp[i][j] += dp[i][j-coins[i-1]]
return dp[n][amount]
For example, if we have coins = [1, 2, 5] and amount = 5, then the function should return 4, because there are four combinations of coins that make up an amount of 5: [1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 2, 2], and [5].
Learn more about dynamic programming
https://brainly.com/question/30868654
#SPJ4