Enter the improper fraction as a mixed number. 5\2
Answers
Answer:2 1/2
Step-by-step explanation:
Related Questions
how many apples does john eat
Answers
Answer:
you gave no context....so ill just guess 3.
negative four and one third ÷ two and one fifth
Answers
Answer:
-65/33
Step-by-step explanation:
The solution to the given expression negative four and one third ÷ two and one fifth is -1 32/33
Fraction divisionnegative four and one third ÷ two and one fifth
-4 1/3 ÷ 2 1/5
= -13/3 ÷ 11/5
Multiply by the reciprocal of 11/5The reciprocal of 11/5 is 5/11= -13/3 × 5/11
= (-13 × 5) / (3 × 11)
= -65 / 33
= -1 32/33
Therefore, the solution to the fraction is -1 32/33
Learn more about fraction:
https://brainly.com/question/11562149
#SPJ1
in exercises 3-6 identify the function family to which f belongs f(x)=2|x + 2| -8
Answers
The given function belongs to the linear family.
According to the statement
we have to find that the type which is belongs to the function f.
So, for this purpose, we know that the
To identify the function family, we do the following
Identify the variable --- the variable of the function is x
Check if the variable has any negative exponent -- x has no negative power
Identify the highest power of x -- The highest power of x is 1.
Then
When there is no negative exponent and the highest power of the variable is 1, then the function belongs to the linear family.
Next, we compare the function to its parent function.
The parent function of a linear function is:
y = x
And it is translated by the 8.
So, The given function belongs to the linear family.
Learn more about function here
https://brainly.com/question/4025726
#SPJ9
F(x)=3x+17 find f(-2)
Answers
Explanation:
f(-2) means you’re substituting in -2 for x.
f(-2) = 3(-2) + 17
f(-2) = 9
Hope this helped! :)
What is the value of for -6a^-3b^2 for a=-2 and b=4?
Answers
Easy buddy....
\( - 6 \times ({ - 2})^{ - 3} \times ({4})^{2} = \)
\( - 6 \times ({ - \frac{1}{2} })^{3} \times 16 = \\ \)
\( - 6 \times ( - \frac{1}{8}) \times 16 = \\ \)
16 simplifies to by 8 and equals 2
\( - 6 \times ( - 2) = 12\)
_________________________________
And we're done.
Thanks for watching buddy good luck.
♥️♥️♥️♥️♥️
We can represent a polynomial in x of degree n using an array A[0..n] such that A[i] is the coefficient of the term x
i
. That is, the polynomial is equal to A[n]⋅x
n
+A[n−1]⋅x
n−1
+⋯+A[1]⋅x+A[0]. Given two arrays P[0..n] and Q[0..n] that represent two polynomials p(x) and q(x) of degree n, respectively, describe a divide-and-conquer algorithm that computes the product p(x)⋅q(x) with a worst-case running time of o(n
2
). That is, the worst-case running time of your algorithm must be asymptotically less than Θ(n
2
). The output of your algorithm is required to be an array R[0..2n] that represents a polynomial in x of degree 2n, i.e., R[2n]⋅x
2n
+R[2n−1]⋅x
2n−1
+⋯+R[1]⋅x+R[0]. Argue that your algorithm is correct. Derive the worst-case running time of your algorithm.
Answers
Using the Master theorem, we can see that the running time is \(O(n^log₂2)\) = O(n), which is less than \(O(n^2).\) Therefore, the algorithm achieves a worst-case running time of \(O(n^2) or o(n^2),\) as required.
To compute the product of two polynomials p(x) and q(x) using a divide-and-conquer algorithm with a worst-case running time of O(\(n^2\)), we can follow the following steps:
1. If the degree of the polynomials P and Q is 0, create a result array R with size 1 and set R[0] as P[0] * Q[0]. Return R.
2. Split the polynomials P and Q into two halves, P₁ and P₂, and Q₁ and Q₂, respectively, by dividing them at the midpoint.
3. Recursively compute the products of the polynomial halves:
- Compute R₁ as the product of P₁ and Q₁.
- Compute R₂ as the product of P₂ and Q₂.
4. Create a result array R with size 2n+1.
5. For each coefficient R[i] in R:
- If i <= n, compute R[i] by summing the corresponding coefficients from R₁ and R₂, i.e., R[i] = R₁[i] + R₂[i].
- If i > n, compute R[i] by subtracting the corresponding coefficients from R₁ and R₂, i.e., R[i] = R₂[i-n-1] - R₁[i-n-1].
6. Return the result array R.
To argue the correctness of the algorithm, we can observe that polynomial multiplication is equivalent to the convolution of the coefficient arrays. The algorithm recursively divides the polynomials into halves, performs multiplications, and combines the results using addition and subtraction. By following this process, we ensure that each coefficient in the resulting array is correctly computed based on the convolution operation.
The worst-case running time of this algorithm can be derived as follows:
- Splitting the polynomials at each recursion step takes O(1) time.
- Performing two recursive calls on halves of size n/2 takes O(log n) time.
- Combining the results by summing and subtracting coefficients takes O(n) time.
- The total worst-case running time can be represented as T(n) = 2T(n/2) + O(n).
Learn more about Master theorem here:
https://brainly.com/question/32611991
#SPJ11
Which of the following is an equation of the line in the graph?

Answers
Answer:
Y= -3X+4
Step-by-step explanation:
Solve:
V5x+1+6=4
V=square root

Answers
Answer:
the answer is c hope it help
Answer: D
Step-by-step explanation:
1. movethe constanat to the right
2. Calculate
3.The statement is false
what’s the area of a regular octagon with apothem 8 inches and each side 9 inches
Answers
288 square inches is the area of the rectangular octagon.
The formula Area = (apothem * perimeter)/2 will be used to calculate the area of a regular octagon.
The apothem is the distance between the center and the midpoint of a side, and the perimeter is the sum of the lengths of all eight sides.
In this instance, the perimeter is indicated as 8 inches for the apothem and 9 inches for each side.
Perimeter = 8 * 9 inches = 72 inches
Now we can use the formula to find the area:
Area = (apothem * perimeter)/2
Area = (8 inches * 72 inches)/2
Area = 288 square inches
Therefore, the area of the regular octagon is 288 square inches.
Learn more about Area here:
https://brainly.com/question/27683633
#SPJ1
PLS HELP
Melanie is mixing a cleaning solution that takes 4 parts water, 7 parts Chlorox, and 2 parts lavender. If she uses 8 cups of water, how many cups will be made of the cleaning solution as a whole?
Answers
Answer:
26 cups
Step-by-step explanation:
4 : 7 : 2 doubled, because 8 cups of water is 2 x 4
= 8 + 14 + 4 = 26 cups
Write the domain of the given functions in interval notation. a) f(x) = 13x-15 / 20x-14b) f(x) = √20x-14c) f(x) = 13x² - 14x + 20d) f(x) = ³√13x - 15e) f(x) = √20-14x
Answers
The following can be answered by the concept of Domain.
a. The domain in interval notation is (-∞, 7/10) ∪ (7/10, ∞).
b. The domain in interval notation is [7/10, ∞).
c. The domain in interval notation is (-∞, ∞).
d. The domain in interval notation is (-∞, ∞).
e. The domain in interval notation is (-∞, 10/7].
a) For f(x) = (13x-15) / (20x-14), the domain is all real numbers except for values of x that make the denominator equal to zero. So, 20x-14 ≠ 0. Solving for x, x ≠ 7/10. The domain in interval notation is (-∞, 7/10) ∪ (7/10, ∞).
b) For f(x) = √(20x-14), the domain is all values of x that make the expression under the square root non-negative. So, 20x-14 ≥ 0. Solving for x, x ≥ 7/10. The domain in interval notation is [7/10, ∞).
c) For f(x) = 13x² - 14x + 20, the domain is all real numbers since it is a quadratic function. The domain in interval notation is (-∞, ∞).
d) For f(x) = ³√(13x - 15), the domain is all real numbers since the cube root is defined for any real number. The domain in interval notation is (-∞, ∞).
e) For f(x) = √(20-14x), the domain is all values of x that make the expression under the square root non-negative. So, 20-14x ≥ 0. Solving for x, x ≤ 10/7. The domain in interval notation is (-∞, 10/7].
To learn more about Domain here:
brainly.com/question/29531272#
#SPJ11
in investigation 2, if you were to double the length of the paper strip you dropped through the tape timer, would the number of dots on the paper also double?
Answers
Yes, when the length of the paper strip doubles, so will the number of dots on it.
Yes, when the length of the paper strip doubles, so will the number of dots on it. This is the case because the dots are uniformly spaced apart, and the total number of spaces between the dots doubles as the length of the strip does. As a result, to occupy the same number of spaces as the strip's length, the number of dots must also double. The same rule holds true for every paper strip of any length; increasing the strip's length will result in doubling the number of dots on it. The quantity of dots on the paper strip is therefore directly proportional to the length.
Learn more about length here
https://brainly.com/question/13194650
#SPJ4
In a lottery game, a single ball is drawn at random from a container that contains 25 identical balls numbered from 1 through 25. Find the probability that the number drawn is even or a multiple of 9.
The probability that the number drawn is even or a multiple of 9 is _________
(Type an integer or a decimal.)
Answers
The probability that the number drawn is even or a multiple of 9 is 14/25, which simplifies to 0.56 or 56%.
To find the probability that the number drawn is even or a multiple of 9, we need to determine the number of favorable outcomes and divide it by the total number of possible outcomes.
There are a total of 25 balls numbered from 1 through 25 in the container.
Even numbers: Out of the 25 balls, half of them are even numbers (2, 4, 6, ..., 24). So there are 25/2 = 12.5 even numbers, but since we cannot have a fraction of a ball, we consider it as 12 even numbers. Multiples of 9: Out of the 25 balls, the multiples of 9 are 9, 18, and 27 (which is not in the container). So there are 2 multiples of 9.
Now we sum up the favorable outcomes: 12 even numbers + 2 multiples of 9 = 14 favorable outcomes. The total number of possible outcomes is 25 (since there are 25 balls in total).
Therefore, the probability that the number drawn is even or a multiple of 9 is 14/25, which simplifies to 0.56 or 56%.
LEARN MORE ABOUT probability here: brainly.com/question/32117953
#SPJ11
Let's Try it out (2 Steps)The population of a once very popular city of 250,000people has been decreasing by 3.5% each year,Write an exponential decay function that represents thepopulation after t years,y = a[1 – r)'250,000(1 - 3.5)Simplify!250,000(.035)Use your model to approximate what the population willbe 7 years from now.*Round answer to the nearest WHOLE number
Answers
The population at the onset as 250,000. There has been a 3.5% decrease every year.
The exponential decay function therefore is;
\(\begin{gathered} y=a(1-r)^t \\ a=250000,r=0.035,t=\text{time in years} \end{gathered}\)Hence, to approximate what the population would be 7 years from now;
\(\begin{gathered} y=a(1-r)^t \\ y=250000(1-0.035)^7 \\ y=250000(0.965)^7 \\ y=250000\times0.779275\ldots \\ y=194818.9516 \\ y\approx194819\text{ (to the nearest whole number)} \end{gathered}\)The population after 7 years shall be 194,819 people (rounded to the nearest whole number).
What is the slope of the line? Write your answer in decimal format
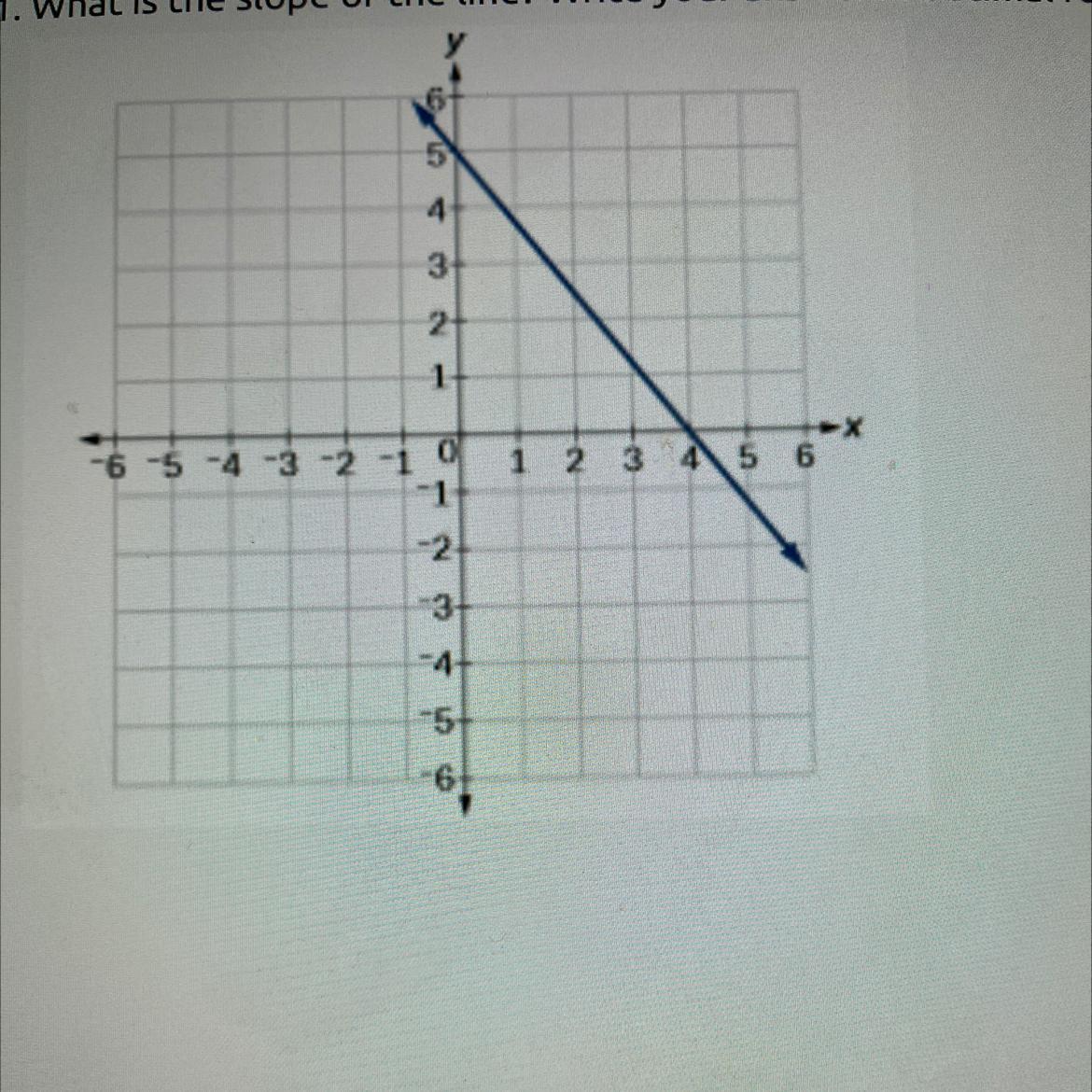
Answers
Answer:
-1.25
Step-by-step explanation:
To find the slope you must use 2 points. For this graph, two points that work are (0,5) and (4,0). Then find the rise over run, which is the change in y over the change in x. Do this by using the slope formula, \(\frac{y_{2} - y_{1} }{x_{2}- x_{1} }\). Once plugged in this should simplify to -5/4. In decimal form, this equals -1.25.
Please HELP!!!! Asappppp thank you!!!!
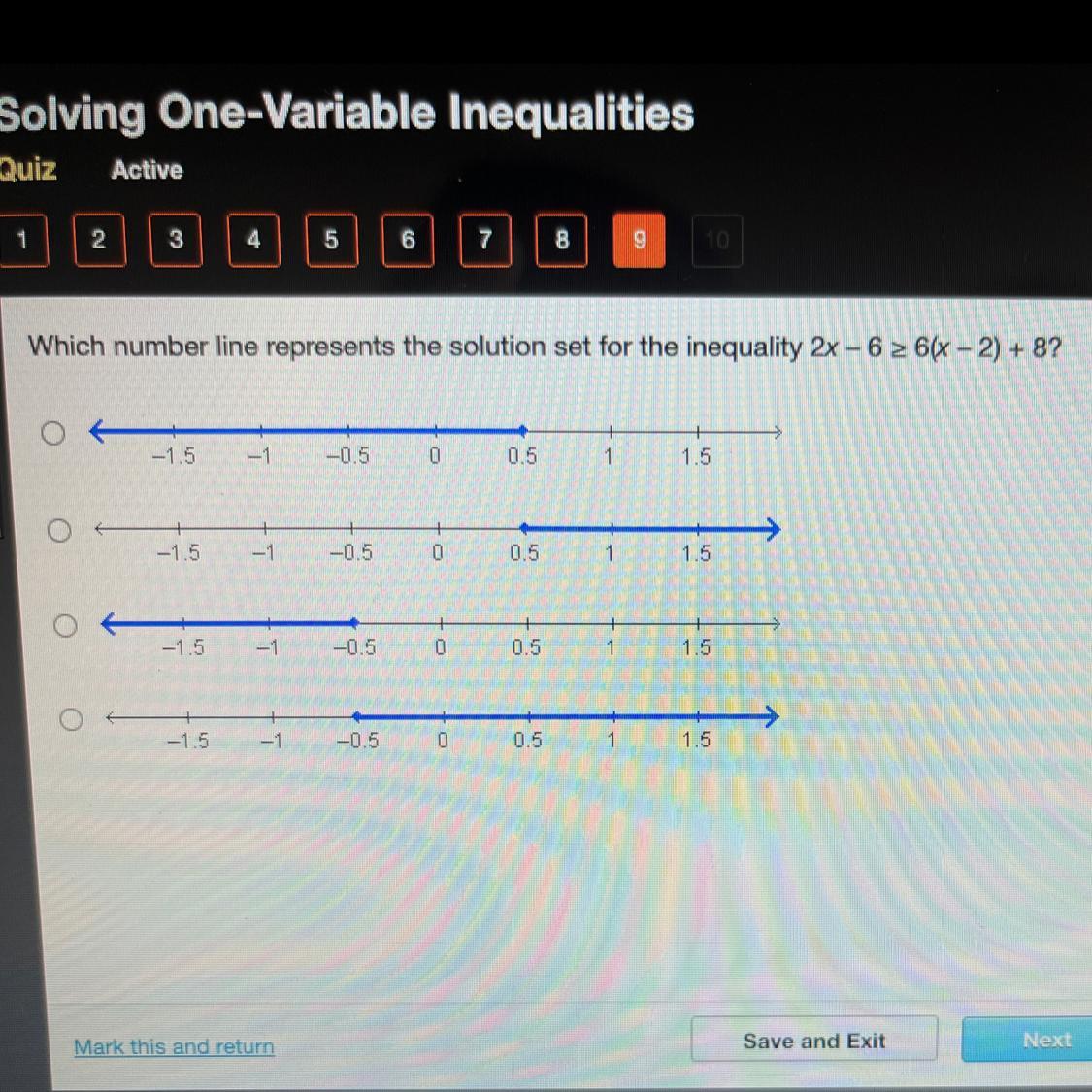
Answers
Answer:
Step-by-step explanation:
The answer is C
is 5/2 rational or irrational
Answers
Answer:
Rational
Step-by-step explanation:
Any number that is written in fraction form is rational. Thus, making 5/2 rational.
Best of Luck!
Answer:
rational
Step-by-step explanation:
A rational number can be expressed in the form
\(\frac{a}{b}\) ← where a and b are integers
\(\frac{5}{2}\) is in this form and is rational
Use logarithmic differentiation to find the derivative of the function y= x²/x y'(x)= 2 + 1 In x) x²
Answers
To use logarithmic differentiation to find the derivative of the function y = x²/x, we first take the natural logarithm of both sides:
ln(y) = ln(x²/x)
Using the properties of logarithms, we can simplify this to:
ln(y) = 2 ln(x) - ln(x)
Now we differentiate both sides with respect to x using the chain rule:
1/y * y' = 2/x - 1/x
Simplifying this expression, we get:
y' = y * (2/x - 1/x²)
Substituting back in the original expression for y, we have:
y' = x²/x * (2/x - 1/x²)
Simplifying further, we get: y' = 2x - 1/x
Therefore, the derivative of the function y = x²/x using logarithmic differentiation is y' = 2x - 1/x.
Learn more about logarithmic differentiation,
https://brainly.com/question/31299592
#SPJ11
its a timed testttt Do all five get brainliest fifty points and ill do any dare you want lol
3/5(x−7/10)=−3 1/4
5(x−3 3/4)=7 1/2
−1/5(x+1 3/4)=−2 1/2
−3/4(x+2)=6
2/5(−3.6−x)=5
Answers
Answer:
1. x=-283/60
2. x=21/4
3. x=43/4
4. x= -10
5. x= -16.1
Step-by-step explanation:
What is the solution to the linear equation?
d - 10 - 2d + 7 = 8+ d - 10 - 3d
Answers
Answer:
1
Step-by-step explanation:
d-10-2d+7=8+d-10-3d
Simplify both sides
-d-3=-2d-2
Now add 2d to both sides
d-3=-2
Add 3 to both sides
d=1
need help with these!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!



Answers
Answer:
Step-by-step explanation:

Given f(x)=−3x+4, what is f(2)?
Answers
Answer:
Step-by-step explanation:

what is 1-1 i wanna know because i dont know
Answers
Answer:
Step-by-step explanation: 0
Answer:
0
Step-by-step explanation:
no explanation needed
A 5 foot tall person standing near a tree casts a shadow 8 feet long. At the same time, the tree casts a shadow that is 24 feet long. The triangles shown in the diagram are similar.
What is the value of x, the height of the tree?
30 ft.
12 ft.
15 ft.
2.5 ft.
Answers
The height of the tree is 15 feet. Option C
What is proportion?Proportion can simply be defined as an arithmetic comparison between two quantities, numbers or elements.
It is also described as an equation where two given ratios are made equal or equivalent to each other.
From the information given, we have that;
5 foot tall person casts a shadow 8 feet longThe tree casts a shadow that is 24 feet long.To determine the height of the tree 'x', we have;
If 5 feet = 8 feet long shadow
Then x feet = 24 feet long
cross multiply
8 × x = 24 × 5
Multiply through
8x = 120
Divide both sides by 8, we have;
x = 120/8
x = 15 feet
Hence, the height is 15 feet
Learn more about proportion here:
https://brainly.com/question/1781657
#SPJ1
What is the value of x in the equation: 3x – 5x + 10 = 36
Answers

Answer:
-13
Step-by-step explanation:
3x-5x+10=35
-2x+10=36
-2x=36-10
-2x\-2=26\-2
x=-13
3.) Graph on Geogebra the linear equation y=2x, then select the correct 10 points
line: *
O Blue line
Green line
Black line
Red line
Answers
i need help plss its a spring break thing and i need help

Answers
Answer:
It's B, because thats where the two points cross
Step-by-step explanation:
The temperature in the morning was -2 degrees. The temperature is dropping at a constant rate, and 4 hours later the temperature is now -22 degrees. How many degrees did the temperature change each hour?
Answers
Given:
Temperature in the morning = -2 degrees.
Temperature is dropping at a constant rate.
Temperature after 4 hours = -22 degrees.
To find:
The rate of change of temperature.
Solution:
Let y be the temperature after x hours from the morning.
Temperature in the morning is -2 degrees. It means, the ordered pair is (0,-2).
4 hours later the temperature is now -22 degrees. It means, the ordered pair is (4,-22).
Now, formula for average rate of change or slope is
\(m=\dfrac{y_2-y_1}{x_2-x_1}\)
\(m=\dfrac{-22-(-2)}{4-0}\)
\(m=\dfrac{-22+2}{4}\)
\(m=\dfrac{-20}{4}\)
\(m=-5\)
Therefore, the change in temperature is -5 per hour. It means the permutate is decreasing by 5 degrees per hour.
How do you know if triangles are congruent in SAS?
Answers
With the help of the figure we can say that triangles are congruent by SAS Rule
What is Congruence of Triangle?
Triangle congruence: Two triangles are said to be congruent if all three of their corresponding sides are equal and all three of their corresponding angles are equal in size. These triangles can be moved, rotated, flipped, and turned to look exactly the same.
Solution:
By SAS rule, two triangles are said to be congruent if any two sides and the angle included between the sides of one triangle are comparable to the corresponding two sides and the angle included between the sides of the second triangle.
In given figure, sides AB= PQ, BC=QR and angle between AB and BC equal to angle between PQ and QR i.e. ∠B = ∠Q. Hence, Δ ABC ≅ Δ PQR.
To learn more about Congruence of Triangles from the given link
https://brainly.com/question/2938476
#SPJ4

HELP plz answer this!

Answers
Answer:
see explanation
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Given
y = \(\frac{2}{3}\) x + 3 ← in slope- intercept form
with slope m = \(\frac{2}{3}\)
Given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{\frac{2}{3} }\) = - \(\frac{3}{2}\)
His error was in missing the negative sign from \(\frac{3}{2}\)