Emanuel was charged \$32$32dollar sign, 32 for a 14\dfrac29 \text{ km}14
9
2
km14, start fraction, 2, divided by, 9, end fraction, start text, space, k, m, end text taxi ride. The cost per kilometer is constant. As a simplified proper fraction
Answers
The cost per kilometer for Emanuel's taxi ride is given as follows:
$9/4.
How to obtain the cost per kilometer?To obtain the cost per kilometer of the tax ride, we apply the proportion, dividing the total cost by the distance of the taxi ride.
From the text given in this problem, the parameters are given as follows:
Total cost: $32.Total distance: 14 and 2/9 kilometers = 14 + 2/9 kilometers = 14.22 kilometers. (conversion of mixed number to decimal).Then the cost per kilometer for Emanuel's taxi ride is found applying the proportion as follows:
Cost per kilometer = 32/14.22 = 2.25.
We have that the fraction equivalent of .25 is given as follows:
1/4.
Thus the proper fraction that represents the cost is given as follows:
2 + 1/4 = 8/4 + 1/4 = $9/4.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Related Questions
Given lines p and q are parallel, find the value of x that makes each diagram true.
Answers
In the given diagram the value of x is is 140° and 25° respectively
In the diagram a, when you have 2 parallel lines cut by a transversal, the corresponding angles are equal and the value of x is equal to the corresponding angle as they are vertical angles, vertical opposite angles are equal.
In the diagram b, angle x is equal to the angle that is supplementary to 155° (Sum of supplementary angles is equal to 180°)
180-155=25°
In the given diagram the value of x is 140° in the diagram a and 25° for the diagram b respectively
To learn more about parallel line refer here
https://brainly.com/question/16742265
#SPJ9
Your question is incomplete as the diagram is missing but the above answer might help you out.
A survey team is trying to estimate the height of a mountain above a level plain. From one point on the plain, they observe that the angle of elevation to the top of the mountain is 27∘. From a point 1500 feet closer to the mountain along the plain, they find that the angle of elevation is 30∘. How high (in feet) is the mountain?
Answers
Answer:
3394 ft.
Step-by-step explanation:
I don't know I used a web browser and found the answer on a website.
Answer:
9459.9771875106 ft.
Step-by-step explanation:
Took the test
chance of failure is independent of another's failure, what would the individual failure rate need to be so that our of 20 users only 20% failed
Answers
The individual failure rate needs to be approximately 3.33% for only 20% of 20 users to fail, assuming that the probability of failure is independent of another's failure.
If the chance of failure is independent of another's failure, it means that the probability of each individual failing is the same, and we can assume that the failures follow a binomial distribution.
Let p be the probability of an individual failing, and n be the number of trials (in this case, the number of users, n = 20).
The probability of exactly k failures out of n trials is given by the binomial probability formula:
\(P(k) = (n choose k) \times p^k \times (1-p)^{(n-k)\)
where (n choose k) is the binomial coefficient, equal to n! / (k! × (n-k)!).
To find the individual failure rate needed for 20% of 20 users to fail, we need to solve for p such that P(4) = 0.2, where k = 4 is the number of failures we want to allow.
P(4) = (20 choose 4) \(\times p^4 \times (1-p)^{(20-4) }= 0.2\)
Using a binomial calculator or software, we can solve for p and get:
p ≈ 0.0333 or 3.33%
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Heights of men in America have a normal distribution with a mean of 69.5 9nches and a standard deviation of 3 inches. Perform the following calculations.. Let X represent the mean height of a random sample of n American adult men. Find n if P(68.52 < X <70.48) = .95.? If 100 American men are chosen at random, find the probability that at least 25 of them are shorter than 68 inches. Hint, let Y be the number of Americans shorter than 68, then Y is binomial. Find the probability using a normal approximation?
Answers
The probability between these two z-scores to be 0.95. In other words P(z₁ < Z < z₂) = 0.95
What is probability?
Probability is a branch of mathematics that deals with the study of random events or phenomena. It is the measure of the likelihood that an event will occur or not occur, expressed as a number between 0 and 1, where 0 represents impossibility and 1 represents certainty.
To find the value of n in the first calculation, we need to determine the sample size that results in a probability of 0.95 for the interval (68.52 < X < 70.48).
For a normal distribution, we can calculate the z-scores corresponding to the given values of X using the formula:
z = (X - μ) / (σ / √n)
where μ is the population mean, σ is the population standard deviation, and n is the sample size.
Given:
μ = 69.5 inches
σ = 3 inches
For the lower bound, X = 68.52 inches:
z₁ = (68.52 - 69.5) / (3 / √n)
For the upper bound, X = 70.48 inches:
z₂ = (70.48 - 69.5) / (3 / √n)
We want the probability between these two z-scores to be 0.95. In other words:
P(z₁ < Z < z₂) = 0.95
We can convert this probability to the standard normal distribution using the z-table or calculator. The z-table gives the area to the left of the z-score, so we can calculate:
P(Z < z₂) - P(Z < z₁) = 0.95
Now, we can look up the z-scores in the standard normal distribution table and find their corresponding probabilities. Let's assume the values to be Z₁ and Z₂.
P(Z < Z₂) - P(Z < Z₁) = 0.95
Now, substitute the values of Z₁ and Z₂ using the calculated z-scores:
P(Z < z₂) - P(Z < z₁) = 0.95
By solving this equation, we can determine the value of n.
For the second calculation, we need to find the probability that at least 25 out of 100 randomly chosen American men are shorter than 68 inches. We can approximate this probability using the normal approximation to the binomial distribution.
Let Y be the number of Americans shorter than 68 inches among the 100 randomly chosen men. The probability of Y can be approximated using the normal distribution with mean (np) and standard deviation (sqrt(np(1-p))), where n is the sample size and p is the probability of success in a single trial.
In this case, n = 100 and p is the probability that a randomly chosen American man is shorter than 68 inches. To calculate p, we need to find the area to the left of 68 inches in the normal distribution with mean 69.5 inches and standard deviation 3 inches.
Once we have the values of np and (np(1-p)), we can use the normal distribution to find the probability that at least 25 men are shorter than 68 inches by calculating:
P(Y >= 25) = 1 - P(Y < 25)
We can use the calculated mean and standard deviation to approximate this probability using the normal distribution.
Hence, the probability between these two z-scores to be 0.95. In other words P(z₁ < Z < z₂) = 0.95
To know more about probability visit :
https://brainly.com/question/13604758
#SPJ4
PLZ HELP WILL GIVE BRAINLIEST TO CORRECT ANSWER!!!
Completely factor the following polynomial: 8x^3−125
Answers
Answer:
(2x-5)(4x^2+10x+25)
Explanation:
Factoring difference of cubes (a3−b3): (a−b)(a2+ab+b2)
Here, a is 2x because the cube root of 8 is 2 and the cube root of x3 is x, b is 5 because the cube root of 125 is 5.
Plug the numbers in:
(2x−5)((2x)2+2x⋅5+52)
(2x−5)(22x2+10x+25)
(2x−5)(4x2+10x+25)
Answer:
8x^3 can also be written as \((2x)^{3}\).
-125 can also be written as \(-5^{3}\).
Factoring the polynomial:
\((2x)^3+(-5)^3\)
Here's a graph of a linear function. Write the equation that describes that function.
Express it in slope-intercept form.

Answers
respectively Q 1
=160−10P 1
OR r 1
=16−0.1Q 1
aWD 1/P 6
=16 6
−2T −
Q 2
=200−20P 2
ORP 2
=10−0,050,…H1AP 2
=15−0:0% Saga's Total Cost function is: TC =120+4Q With third degree price discrimination, the condition for peofit marimizater is MR 1
=MR 2
=MR=MC Find P 1
,Q 1
,P 2
,Q 1
Total Revenue, Total Cost, and Total proft wit sree discrimination. Find P,Q,TR,TC&π In the absence of price discrimination. Marks: 7
Answers
In the absence of price discrimination, the profit-maximizing conditions would be different, and the resulting prices, quantities, total revenue, total cost, and profit would also be different.
To find the profit-maximizing conditions with third-degree price discrimination, we need to equate the marginal revenue (MR) to the marginal cost (MC) for each market segment.
Given the demand equations and the total cost function:
Market 1: Q1 = 160 - 10P1 or P1 = 16 - 0.1Q1
Market 2: Q2 = 200 - 20P2 or P2 = 10 - 0.05Q2
Total Cost: TC = 120 + 4Q
To find the profit-maximizing prices and quantities, we equate MR to MC for each market segment:
MR1 = MC:
16 - 0.2Q1 = 4
0.2Q1 = 12
Q1 = 60
MR2 = MC:
10 - 0.1Q2 = 4
0.1Q2 = 6
Q2 = 60
Substituting the quantities back into the demand equations, we find:
P1 = 16 - 0.1(60) = 10
P2 = 10 - 0.05(60) = 7
The total revenue (TR) can be calculated by multiplying the price by the quantity for each market segment:
TR = P1 * Q1 + P2 * Q2
TR = (10 * 60) + (7 * 60)
TR = 600 + 420
TR = 1020
The total cost (TC) is given by the total cost function:
TC = 120 + 4Q
TC = 120 + 4(60 + 60)
TC = 120 + 480
TC = 600
Finally, the profit (π) can be calculated by subtracting total cost from total revenue:
π = TR - TC
π = 1020 - 600
π = 420
In the absence of price discrimination, the profit-maximizing conditions would be different, and the resulting prices, quantities, total revenue, total cost, and profit would also be different.
Learn more about absence here:
https://brainly.com/question/30062518
#SPJ11
A result is called "statistically significant" whenever. O The null hypothesis is true. O The significant level a = 0.05. O The p-value Greaterthanorequalto 0.05. O The p-value is less than the significant level.
Answers
A result is called "statistically significant" when the p-value is less than the significant level, typically 0.05.
This means that there is less than a 5% chance that the results are due to chance alone, and suggests that there is a real effect present in the data.
The Null Hypothesis is the assumption that there is no significant difference between the measured phenomenon and a certain value or set of values. A statistically significant result means that the observed data are inconsistent with the assumption of no difference, or no effect.
To know more about Null Hypothesis click on the link provided below:
https://brainly.com/question/28920252#
#SPJ4
Brainliest for the correct awnser
What number completes the following sequence?
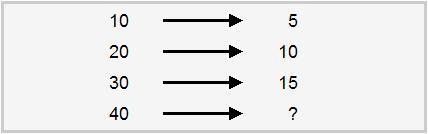
Answers
Answer:
20
Step-by-step explanation:
Because it half of 40
The set below contains which types of numbers -1,5,1/2,15,3.75,36,square root 81, 100
Answers
Answer:
i need help
Step-by-step explanation:
Tekan-Tekan Sdn. Bhd. has order for 200 Model AS-120 calculator for delivery on day 200. The calculator consists of three parts. Components 2 and 3 form subassembly 1 . Sub-assembly 1 and component 4 form the final assembly. Following are the work centers and times of each operation. Table Q3(a) shows routine file of the operation. Assuming: - Only one machine is assigned to each operation - The factory works on 8-hour shift, 5 days a week - All parts move in one lot of 200. (a) Illustrate the backward schedule based on the information given above. (12 marks) (b) Identify when component 3 must be started to meet the delivery date. (2 marks)
Answers
Component 3 must be started on day 197 to meet the delivery date of day 200.
To illustrate the backward schedule, we need to start from the delivery date (day 200) and work our way backward, taking into account the lead times and dependencies of each operation.
(a) Backward schedule:
Operation | Work Center | Time (hours) | Start Day
--------------------------------------------------------
Final Assembly | Work Center 1 | 1 | 200
Sub-assembly 1 | Work Center 2 | 2 | 199
Component 4 | Work Center 3 | 3 | 197
Component 2 | Work Center 4 | 4 | 196
Component 3 | Work Center 5 | 3 | ????
(b) To identify when component 3 must be started to meet the delivery date, we need to consider its dependencies and lead times.
From the backward schedule, we see that component 3 is required for sub-assembly 1, which is scheduled to start on day 199. The time required for sub-assembly 1 is 2 hours, which means it should be completed by the end of day 199.
Since component 3 is needed for sub-assembly 1, we can conclude that component 3 must be started at least 2 hours before the start of sub-assembly 1. Therefore, component 3 should be started on day 199 - 2 = 197 to ensure it is completed and ready for sub-assembly 1.
Hence, component 3 must be started on day 197 to meet the delivery date of day 200.
Learn more about Scheduling here:
brainly.com/question/30012511
#SPJ4
Rotate 180° then Rotate 270° CC (2,-5)
Answers
After the rotation of the point, we get the point as (5, 2)
We are given a point:
C (2, -5)
We first need to rotate it 180°.
When rotating a point 180 degrees counterclockwise about the origin our point A(x, y) becomes A'(-x, -y). So all we do is make both x and y negative.
So, we get the point as:
( - 2 , 5 )
Now, we need to rotate it 270°
The algebraic rule for a figure that is rotated 270° clockwise about the origin is (y, -x).
So, we get the point as:
(5, 2)
Therefore, after the rotation of the point, we get the point as (5, 2)
Learn more about rotation of a point here:
https://brainly.com/question/26249005
#SPJ9
PLEASE ANSWER THE FOLLOWING QUESTION GIVEN THE CHOICES!!!

Answers
Answer: 3/52
Step-by-step explanation:
You want to pick a diamond jack, diamond queen or diamond king
There are only 3 of those so
P(DJ or DQ or DK) = 3/52 There are 3 of those out of 52 total
"
Evaluate the following definite integral using either Gamma or Beta
Functions only:
" (a) √√z e-√z dz (b) (ex)² (e²x + 1)¯³dx
Answers
The definite integral in part (a) cannot be evaluated using only Gamma or Beta functions.
To evaluate the integral ∫√√z e^(-√z) dz using only Gamma or Beta functions, we need to express the integrand in terms of such functions. However, the integrand in this case does not have a direct representation in terms of Gamma or Beta functions. Therefore, we cannot evaluate the integral using only those functions.
Part (b):
To evaluate the integral ∫(e^x)^2 (e^(2x) + 1)^(-3) dx using only Gamma or Beta functions, we can make a substitution: let u = e^x. Then, du = e^x dx, and the integral becomes ∫u^2 (u^2 + 1)^(-3) du. This can be rewritten as ∫u^2 (1 + u^(-2))^(-3) du.
Now, we can rewrite the integrand using the Beta function as (1/u^2)^(-3/2) * (1 + u^(-2))^(-3) = Beta(-3/2, -3) = Γ(-3/2)Γ(-3)/Γ(-6/2).
Using the properties of the Gamma function, we have Γ(-3/2) = -4√π/3, Γ(-3) = 2, and Γ(-6/2) = -4√π/15. Substituting these values back into the expression, we get (-4√π/3)(2)/(-4√π/15) = 10/3.
Therefore, the value of the integral ∫(e^x)^2 (e^(2x) + 1)^(-3) dx is 10/3.
For more questions like Integral click the link below:
https://brainly.com/question/22008756
#SPJ11
Tim used a lever to lift a heavy box off the ground. His input work was 50 J and the output work was 40 J. What was the mechanical efficiency of the lever?
A.90%
B.30%
C.80%
D.10%
Answers
Explanation: 40 divided by 50 is .80
Equaling 80%
Please help me now plz I will mark you brainliest

Answers
Answer:
Neither
Step-by-step explanation:
It can be paralel because they both pass through -7 and it cant be perpendicular because the dont intersect at a 90 degree angle
What did I do wrong? Need help with this equation

Answers
Solve the system
\(\begin{bmatrix}y=4x-8 \\ y=2\mleft(x-3\mright)^2-2\end{bmatrix}\)Subtract the equations
\(\begin{gathered} y-y=4x-8-\mleft(2\mleft(x-3\mright)^2-2\mright) \\ 0=4x-8-2(x-3)^2+2 \\ 0=4x-8-2(x^2-6x+9)+2 \\ 0=4x-8-2x^2+12x-18+2 \\ 0=16x-24-2x^2 \\ 0=-2x^2+16x-24 \end{gathered}\)Solve quadratic equation
\(\begin{gathered} 0=-2(x^2-8x+12) \\ 0=-2(x-2)x-6) \end{gathered}\)Then, the solutions are:
\(\begin{gathered} x-2=0 \\ x-2+2=0+2 \\ x=2 \\ \text{For y} \\ y=4(2)-8=8-8=0 \end{gathered}\)And
\(\begin{gathered} x-6=0 \\ x-6+6=0+6 \\ x=6 \\ \text{For y } \\ y=4(6)-8=24-8=16 \end{gathered}\)Answer:
(2,0)
(6,16)
determine the interval of convergence for the taylor series of f(x)=−14/x at x=1. write your answer in interval notation.
Answers
This limit is less than 1 if and only if |x-1| < 1/6, so the interval of convergence is: (1-1/6, 1+1/6) = (5/6, 7/6)
The Taylor series for f(x) = -14/x centered at x=1 is:
\(f(x) = f(1) + f'(1)(x-1) + f''(1)(x-1)^2/2! + f'''(1)(x-1)^3/3! + ...\)
Taking the derivatives of f(x), we have:
f(x) = -14/x
\(f'(x) = 14/x^2\)
\(f''(x) = -28/x^3\)
\(f'''(x) = 84/x^4\)
Evaluating these at x=1, we get:
f(1) = -14
f'(1) = 14
f''(1) = -28
f'''(1) = 84
Substituting these values into the Taylor series, we get:
\(f(x) = -14 + 14(x-1) - 28(x-1)^2/2! + 84(x-1)^3/3! - ...\)
To determine the interval of convergence, we can use the ratio test:
\(lim_{n- > inf} |a_{n+1}(x-1)/(a_n(x-1))| = lim_{n- > inf} |(84/(n+1))/(14/n)| |x-1| = |6(x-1)|.\)
For similar question on convergence.
https://brainly.com/question/31385080
#SPJ11
The interval of convergence for the Taylor series of f(x) = -14/x at x = 1 is (0, 2) in interval notation.
To determine the interval of convergence for the Taylor series of f(x) = -14/x at x = 1, we first find the Taylor series representation. Since f(x) is a rational function, we can rewrite it as f(x) = -14(1/x) and then use the geometric series formula:
f(x) = -14Σ((-1)^n * (x - 1)^n), where Σ is the summation symbol and n runs from 0 to infinity.
To find the interval of convergence, we use the ratio test. The ratio test involves taking the limit as n approaches infinity of the absolute value of the ratio of consecutive terms:
lim (n→∞) |((-1)^(n+1)(x - 1)^(n+1))/((-1)^n(x - 1)^n)|
Simplify the expression:
lim (n→∞) |(x - 1)|
For convergence, this limit must be less than 1:
|(x - 1)| < 1
This inequality gives us the interval of convergence:
-1 < (x - 1) < 1
Add 1 to each part:
0 < x < 2
So, the interval of convergence for the Taylor series of f(x) = -14/x at x = 1 is (0, 2) in interval notation.
Visit here to learn more about Taylor series :
brainly.com/question/29733106
#SPJ11
11. A line through points (-5, 2) and (2, y) has a slope of 3.
Find y.
Help
Answers
Answer:
23
Step-by-step explanation:
Create an equation to find y: 3 = \(\frac{y-2}{2-(-5)}\)Calculate by adding: 3 = \(\frac{y-2}{7}\)Multiply both sides of the equation by 7 : 21 = y - 2 Move the variable to the left-hand side and change its sign : -y + 21 = -2Calculate and change signs : y = 23y = 23
Choose the equation that satisfies the data in the table.
-1 0 1
0
3
6
X
Y
OA. y = 3x +3
B.y = -x +9
Oc.y=x+9
OD. y=-3x +3

Answers
Answer: A: y= 3x + 3
Step-by-step explanation:
The y intercept has to be 3 which is found when x = 0 that eliminates B and C. Then just plug in -1 or 1 into A or D and you will find that plugging in either with get you the y value provided on A.
What is the solution to the following system?
2x - y - 3z = 1
4x + 3y + 2z = -4
-3x + 2y + 5z = -3
Answers
Answer:
(2, - 6, 3)
Step-by-step explanation:
2x - y - 3z = 1 ⇒ y = 2x - 3z - 1 .... (1)
4x + 3y + 2z = - 4 .... (2)
- 3x + 2y + 5z = - 3 .... (3)
(1) ---> (2) and (3)
4x + 3(2x - 3z - 1) + 2z = - 4 ⇔ 10x - 7z = - 1 ... (4)
- 3x + 2(2x - 3z - 1) + 5z = - 3 ⇔ x - z = - 1 ⇒ x = z - 1 ---> (4)
10(z - 1) - 7z = - 1 ⇒ z = 3
x = 2
2(2) - y - 3(3) = 1 ⇒ y = - 6
(2, - 6, 3)
Write 201 in standard form
Answers
Which statements hold true for the function?
f(x) = 3x² - 5
Of(5)
Of(0)=1
f(5)<1
Of(3)
Answers
The statements for the function f( x) = 3x ²- 5 are
f( 5)< 1( false)
f( 0) = 1( false)
Statements for the function f(x) = 3x ²- 5
To find the true or false statement we have to substitute the value for x
First, x= 3
f(x) = 3x ²- 5
f(3)= 3( 5)²- 5
f(3) = 75- 5
f(3)= 70.
Thus, the statement" f( 5)< 1" is false.
Now, at x =0
f(x) = 3x ²- 5
f(0) = 3( 0)²- 5
f(0)= 0- 5
f(0)= -5.
Thus, the statement" f( 0) = 1" is false.
Learn more about Function here:
https://brainly.com/question/30721594
#SPJ1
Solve for the indicated side. Leave your answer in simplified radical form. (Step by step)

Answers
In order to solve this particular question, use the sine rule.
\(\sf sin(x)= \dfrac{opposite}{hypotensue}\)
Here given:
opposite = 6 inchhypotenuse = xangle = 60°Henceforth solve:
\(\hookrightarrow \sf sin(60)= \dfrac{6}{x}\)
\(\hookrightarrow \sf x= \dfrac{6}{sin(60)}\)
\(\hookrightarrow \sf x= 4\sqrt{3}\)
\(\\ \rm\rightarrowtail sin60=\dfrac{Perpendicular}{Hypotenuse}\)
\(\\ \rm\rightarrowtail sin60=\dfrac{6}{x}\)
\(\\ \rm\rightarrowtail \dfrac{\sqrt{3}}{2}=\dfrac{6}{x}\)
\(\\ \rm\rightarrowtail \sqrt{3}x=12\)
\(\\ \rm\rightarrowtail x=12/\sqrt{3}\)
\(\\ \rm\rightarrowtail x=4\sqrt{3}in\)
carl throws a single die twice in a row. for the first throw, carl rolled a 2; for the second throw he rolled a 4. what is the probability of rolling a 2 and then a 4? answer choices are in the form of a percentage, rounded to the nearest whole number.
Answers
To the nearest whole number, the probability of rolling a 2 and a 4 is 2.8%.
A 2 rolling up on the first throw has a 1/6 chance of happening. Given that a 2 was rolled on the first throw, the likelihood of rolling a 4 on the second throw is equally 1/6. We will have to multiply the probabilities to get the probability of both the events happening,
= (1/6)x(1/6)
= 1/36.
We get 2.8% after converting to a percentage and rounding to the next full amount. So, the chance of rolling a 2 and then a 4 is found to be 2.8% chance.
To know more about Probability, visit,
https://brainly.com/question/24756209
#SPJ4
Which function represents exponential decay?
A. f(x) = 0.25(1.06)
B. f(x) = 18 +0.9x
c. f(x) = 412 + 1.03x
D. f(x) = 268(0.86)*
Answers
Answer: The function that represents exponential decay is:
D. f(x) = 268(0.86)^x
This function has a base of 0.86, which is less than 1. As x increases, the value of the function decreases exponentially. This is the characteristic of exponential decay, where the value of a quantity decreases at a constant percentage rate over time.
Option A, f(x) = 0.25(1.06), represents exponential growth, as the base (1.06) is greater than 1.
Option B, f(x) = 18 + 0.9x, represents linear growth, as the value of the function increases linearly with x.
Option C, f(x) = 412 + 1.03x, also represents linear growth, as the value of the function increases linearly with x.
Step-by-step explanation:
17. Algebraically determine the domain and the y -intercept of the function y=\log _{4}(2 x+1)-3 .
Answers
The domain of the function is `R` and the y-intercept is `(0, -3)`
Given, `y = log4(2x + 1) - 3`.
To determine the domain of the function,
we should look for all values of `x` that would make the given function undefined.
There are no real values of `x` that would make the function undefined.
Therefore, the domain of the function is all real numbers or `R`.
To determine the y-intercept, substitute `x = 0` in the given function.`
y = log4(2(0) + 1) - 3 = log4(1) - 3 = 0 - 3 = -3`
Therefore, the y-intercept of the function is `(0, -3)`.
Hence, the domain of the function is `R` and the y-intercept is `(0, -3)`.
To know more about y-intercept visit:
https://brainly.com/question/14180189
#SPJ11
Bayesian analysis of a binary (yes/no) choice may use the
Beta-binomial model
Normal-normal model
Gaussian model
Beta-normal model
None of the above
Answers
The correct answer is the Beta-binomial model. Bayesian analysis is a statistical approach that incorporates prior knowledge or beliefs about a parameter of interest and updates it based on observed data using Bayes' theorem.
In the case of a binary choice, where the outcome can be either yes or no, Bayesian analysis seeks to estimate the probability of success (yes) based on available information.
The Beta-binomial model is a commonly used model in Bayesian analysis for binary data. It combines the Beta distribution, which represents the prior beliefs about the probability of success, with the binomial distribution, which describes the likelihood of observing a specific number of successes in a fixed number of trials.
The Beta distribution is a flexible distribution that is often used as a prior for modeling probabilities because of its ability to capture a wide range of shapes. The Beta distribution is characterized by two parameters, typically denoted as alpha and beta, which can be interpreted as the number of successes and failures, respectively, in the prior data.
The binomial distribution, on the other hand, describes the probability of observing a specific number of successes in a fixed number of independent trials. In the context of Bayesian analysis, the binomial distribution is used to model the likelihood of observing the data given the parameter of interest (probability of success).
By combining the prior information represented by the Beta distribution and the likelihood information represented by the binomial distribution, the Beta-binomial model allows for inference about the probability of success in a binary choice.
The other options mentioned, such as the Normal-normal model and the Gaussian model, are not typically used for binary data analysis. The Normal-normal model is more suitable for continuous data, where both the prior and likelihood distributions are assumed to follow Normal distributions. The Gaussian model is also suitable for continuous data, as it assumes that the data are normally distributed.
In summary, the Beta-binomial model is the appropriate model for Bayesian analysis of a binary choice because it effectively combines the Beta distribution as a prior with the binomial distribution as the likelihood, allowing for inference about the probability of success in the binary outcome.
Learn more about Bayes' theorem at: brainly.com/question/33143420
#SPJ11
Perform the indicated operation.
m/mn + n/m+n =
1. 1/m+n
2. 2
3. 1
4. 2m+n/m+n
Answers
It is used to simplify and combine fractions with different denominators by finding a common denominator.(\(m^{2}\) + 2mn) / (mn+\(n^{2}\)) Thus option D is correct.
How can we perform the operation?To perform the operation:
m/mn + n/m+n
We need to find the LCD (Least Common Denominator) of the fractions, which is mn+n.
Then, we can rewrite each fraction with the LCD and simplify:
m/mn + n/m+n = m(m+n)/(mn+\(n^{2}\)) + n(mn)/(mn+\(n^{2}\))
= m(m+n)/(mn+\(n^{2}\)) + mn/(mn+\(n^{2}\))
= m(m+n) + mn / (mn+\(n^{2}\))
= (\(m^{2}\) + mn + mn) / (mn+\(n^{2}\))
= ( + 2mn) / (m\(m^{2}\)n+\(n^{2}\))
Therefore, (\(m^{2}\) + 2mn) / (mn+\(n^{2}\)), which is option 4.
Learn more about fractions here:
brainly.com/question/10354322
#SPJ1
Answer:
3. 1 is ur answer
Step-by-step explanation: Just did the lesson and got it right
A box office analyst seeks to predict opening weekend box office gross for movies. Toward this goal, the analyst plans to use online trailer views as a predictor.
Answers
Answer and Step-by-step explanation:
A box office predicts to open the weekend box office gross for a movie, and analysts plan to use the online trailer views as a predictor. The 66 movies and the number of the online trailers view from the trailer through the Saturday before the movie and open the weekend box office gross in a million dollars. Linear regression was performed on the data, and the result is the linear regression equation such as Y = -0.724 + 1.41X. At 0.05 level of significance, the linear relationship between the view and opening weekend is as H0: B1 = 0 H1:B is not equal to 0. To compute the test statistic, do the test. The standard error of deviation for this is Syx = 20.702, and the line model is appropriate. Click the icon to view the data on trailer views and open the weekend box office gross. The linear relationship between the trailer views and opening weekend box gross is to compute the test statistics at the level of significance. The test statistic is round to two decimal places as needed, and the p-value is round to three decimal.