ella left the city at 11:13am and got to Tema at 3:08pm. how long did the journey take.
Answers
Answer:
11.13 a.m = 1113 hours
3.08 p.m = 1508 hours
thus, 3 hours 55 minutes
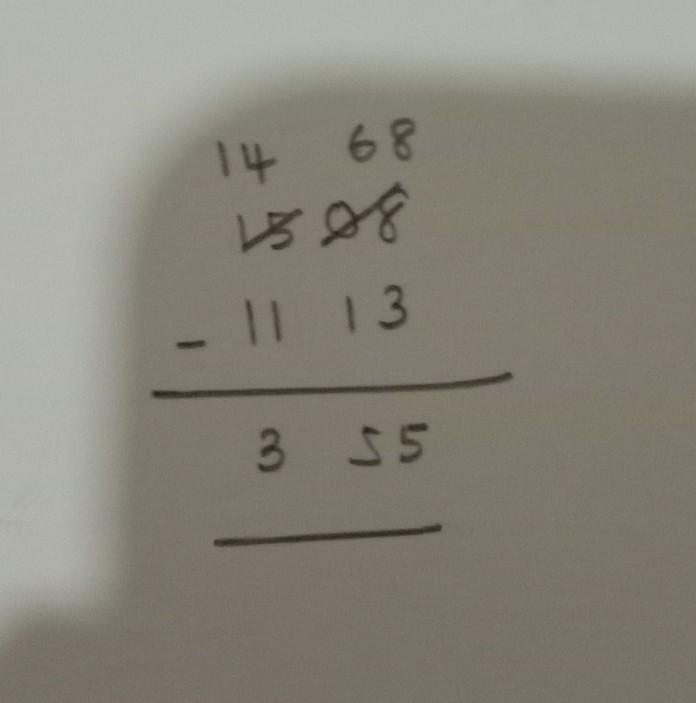
Related Questions
A restaurant customer left $1.05 as a tip. The tax was 8% and the tip was 15% of the cost including tax.
a. Which information is not needed to compute the bill after tax and tip?
b. What was the total bill?
Answers
well, the bill was actually "x", which oddly enough is the 100%, but we also know that the tip was $1.05 and that's 15% of the whole bill plus tax.
so if we know that 1.05 is 15% of "x", what the dickens is "x"?
\(\begin{array}{ccll} amount&\%\\ \cline{1-2} 1.05 & 15\\ x& 100 \end{array} \implies \cfrac{1.05}{x}~~=~~\cfrac{15}{100} \\\\\\ 105=15x\implies \cfrac{105}{15}=x\implies 7=x\)
well, as you can see, we know the tax was 8%, but, it doesn't really matter if it had been 25% or who knows, so long we know that 1.05 is 15% of the whole smack.
what does banana + potato equal?
A Bonato
B Ponana
I'll give brainliest if you get it right :)
Answers
Answer: Bonato
Step-by-step explanation:
help,scatter plots please and thank you

Answers
Answer: D
Step-by-step explanation:
Since a tadpole becomes a frog as it ages, it makes sense that the axis of the tail would go down as it ages since frogs don’t have tails. If you see the x axis as the tempature, and the coats as the y axis. It would make sense that as the tempature gets colder, more people would be buying coats. But basically, D is the only one that doesn’t have a cause and affect, so it wouldn’t have a very linear scatter plot. For example, I have the same letters in my name as someone I know who is 6‘ 4”, and I’m only 4’ 8”. So D wouldn’t make such a nicely formed scatter plot.
If √0.231 = k, then what is the value of √23.1
A. 10k
B. 0.1 k
C. 100k
D. 20k
Answers
Answer:
A
Step-by-step explanation:
using the rule of radicals
\(\sqrt{ab}\) = \(\sqrt{a}\) × \(\sqrt{b}\)
note that 0.231 × 100 = 23.1
given
\(\sqrt{23.1}\)
= \(\sqrt{100(0.231)}\)
= \(\sqrt{100}\) × \(\sqrt{0.231}\)
= 10 × k
= 10k
The value of √23.1 using the value √0.231 = k is 10k.
Thus, option (A) is correct.
Let's first find the value of "k" when √0.231 = k:
√0.231 = k
Now, the value of √23.1 using the value of "k":
√23.1 = √(10 × 2.31)
As √2.31 = k, substitute it in:
√23.1 = √(10 × 2.31)
= √10 × √2.31
= 3.162 × √2.31
Also, √2.31 = 1.52
So, the required value
√23.1 = 3.162 × 1.52
= 4.807
let's check the given options to find the closest value to 4.807:
A. 10k = 10 × √0.231 = 4.807.
B. 0.1k = 0.1 × √0.231 = 0.04806
C. 100k = 100 × √0.231 = 48.06
D. 20k = 20 × √0.231 = 9.6124
Therefore, The value of √23.1 is 10k.
Thus, option (A) is correct.
Learn more about Radical here:
https://brainly.com/question/151386
#SPJ4
simplify
U+U+U
U times U times U
Answers
1). U+U+U = 3U.
2). U time U times U = U x U x U = U³.
What is an expression?One mathematical expression makes up a term. It might be a single variable (a letter), a single number (positive or negative), or a number of variables multiplied but never added or subtracted. Variables in certain words have a number in front of them. A coefficient is a number used before a phrase.
Given:
The two expressions,
U+U+U and U time U times U.
The simplified form of the expression,
U+U+U = 3U.
The simplified form of the expression,
U time U times U = U x U x U.
= U³.
Therefore, the values of the expression are 3U and U³.
To learn more about the expression;
brainly.com/question/24242989
#SPJ1
Which of these is scientific notation?
1.2 x 10^3
20 x 60
2^2 x 3 x 10^2
1,200
Answers
Answer:
1.2×10^3
Step-by-step explanation:
so there it is
What is the mode of the following numbers? 12, 11, 14, 10, 8, 13, 11,9
Answers
Answer:
11 is the mode
Step-by-step explanation: it appears the most
Let f : R → R^n be a differentiable curve such that f'(t) is not equal to 0 for all r ∈ R. Let P be a point that does not belong to the image curve {f(t) | t ∈ R}. If Q = f(t_0) is the point on the curve
closest to P, that is ||P − Q|| ≤ ||P − f(t)|| for all t ∈ R. Show that the vector P − Q is orthogonal to the curve.
Hint: derive the function ||P − f(t)||²
Answers
To show that the vector P - Q is orthogonal to the curve f(t), we derive ||P - f(t)||² and demonstrate that its derivative at t = t₀ is zero, indicating orthogonality between P - Q and f'(t₀).
We start by considering the function ||P - f(t)||², which represents the squared Euclidean distance between P and f(t):
||P - f(t)||² = (P - f(t)) · (P - f(t))
Expanding the dot product, we have:
||P - f(t)||² = ||P||² - 2(P · f(t)) + ||f(t)||²
Next, we differentiate both sides of the equation with respect to t:
d/dt ||P - f(t)||² = d/dt [||P||² - 2(P · f(t)) + ||f(t)||²]
Using the properties of differentiation and the chain rule, we obtain:
d/dt ||P - f(t)||² = -2(P · f'(t)) + 2(f(t) · f'(t))
We want to find the value of t = t₀ such that d/dt ||P - f(t)||² = 0. Setting the derivative equal to zero, we have:
0 = -2(P · f'(t₀)) + 2(f(t₀) · f'(t₀))
Simplifying, we get:
P · f'(t₀) = f(t₀) · f'(t₀)
Since P is a point not on the curve, the vector P - Q is parallel to the tangent vector f'(t₀) at Q. Therefore, P - Q is orthogonal to the curve f(t) at point Q.
To learn more about Euclidean distance click here :
brainly.com/question/30288897
#SPJ11
calculate the average value of f(x) = 8x sec2(x) on the interval [0, π/4].
Answers
The average value of f(x) = 8x sec^2(x) on the interval [0, π/4] is -4/3.
To find the average value of a function f(x) on an interval [a, b], we need to evaluate the definite integral of the function over that interval and divide it by the length of the interval.
The definite integral of f(x) = 8x sec^2(x) over the interval [0, π/4] is given by:
∫[0,π/4] 8x sec^2(x) dx
This integral can be evaluated by substitution. Let u = sec(x) and du = sec(x)tan(x)dxmthen the integral becomes:
∫[0,π/4] 8x sec^2(x) dx = ∫[1,sec(π/4)] 8xu^2du
= 8/3u^3 evaluated at u = sec(π/4) - 8/3u^3 evaluated at u = 1
= 8/3sec^3(π/4) - 8/3 = 8/3(1/cos^3(π/4)) - 8/3 = 8/3*(1/1/2) - 8/3 = 4/3 - 8/3 = -4/3
Thus, The average value of f(x) = 8x sec^2(x) on the interval [0, π/4] is -4/3.
To learn more about definite integrals,
Visit; brainly.com/question/29974649
#SPJ4
the third-degree taylor polynomial for a function f about x=4 is (x−4)3512−(x−4)264 (x−4)4 2. what is the value of f′′′(4)?
Answers
Answer: the value of f′′′(4) is 3/256.
Step-by-step explanation:
Given the third-degree Taylor polynomial:
f(x) = (x−4)³/512 − (x−4)²/64 + (x−4)⁴/2
To find the value of f′′′(4), we need to differentiate the polynomial three times and evaluate it at x = 4.
First derivative:
f'(x) = 3(x−4)²/512 − 2(x−4)/64 + 4(x−4)³/2
Second derivative:
f''(x) = 6(x−4)/512 − 2/64 + 12(x−4)²/2
Third derivative:
f'''(x) = 6/512 + 24(x−4)/2
Now, substitute x = 4 into f'''(x):
f'''(4) = 6/512 + 24(4−4)/2
= 6/512 + 0
= 6/512
= 3/256
Therefore, the value of f′′′(4) is 3/256.
(please help!!!) What is the area of a right triangle with a base of 8 feet and a height of 12 feet?
20 ft2
32 ft2
48 ft2
96 ft2
Answers
Answer:
48 ft2
Step-by-step explanation:
area- 1/2 b*h-
1/2*8*12-
4*12-
48
Find the surface area of a box that has a length of 11.1 cm, a width of 12 cm, and a height of 19.9 cm. Round your answer to the nearest hundredth, but do not include "cm²" with your response.
Answers
The surface area of the box that has a length of 11.1 cm, a width of 12 cm, and a height of 19.9 cm is 1125.96 cm².
To find the surface area of the box, we need to calculate the areas of all six sides and then sum them up.
First, let's calculate the area of the bottom and top faces. Since the length and width are given, we can use the formula for the area of a rectangle: A = length × width.
So the area of the bottom and top faces is 11.1 cm × 12 cm = 133.2 cm² each.
Next, let's calculate the areas of the remaining four sides. We have two pairs of sides with the same dimensions:
11.1 cm × 19.9 cm and 12 cm × 19.9 cm. The areas of these sides are 220.89 cm² and 238.8 cm², respectively.
Now, sum up all six areas:
2 × 133.2 cm² + 2 × 220.89 cm² + 2 × 238.8 cm² = 1125.96 cm².
Therefore, the surface area of the box is 1125.96 cm². Remember to round your answer to the nearest hundredth.
To know more about area of a rectangle visit:
https://brainly.com/question/29133718
#SPJ11
Find the average x-coordinate of the points in the prism D = {(x,y,z):0≤x≤3, 0≤ y ≤15-5x, 0≤z≤3}.
Answers
The limits of integration are given as follows: 0 ≤ z ≤ 3, 0 ≤ y ≤ 15 − 5x, and 0 ≤ x ≤ 3. Hence, the integral becomes, Thus, the average x-coordinate of the points in the prism D is 1.5.
The prism D = {(x, y, z): 0 ≤ x ≤ 3, 0 ≤ y ≤ 15 - 5x, 0 ≤ z ≤ 3}. In order to find the average x-coordinate of the points in the prism D, we will need to use a triple integral, where the integrand is equal to x multiplied by the volume element.Here's the solution:So, average x-coordinate is as follows: Now, use the triple integral. The limits of integration are given as follows: 0 ≤ z ≤ 3, 0 ≤ y ≤ 15 − 5x, and 0 ≤ x ≤ 3. Hence, the integral becomes, Thus, the average x-coordinate of the points in the prism D is 1.5.
To know more about integration visit:
https://brainly.com/question/31744185
#SPJ11
David's gasoline station offers 21 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 30% of all customers pay in cash. During a one-hour period, 15 customers buy gasoline at this station. What is the probability that at least 10 pay in cash
Answers
0.0931 is the probability that at least 10 pay in cash.
What is a probability simple definition?
The ratio of the number of outcomes in an exhaustive set of equally likely outcomes that produce a given event to the total number of possible outcomes.
Using binomial distribution with n= 15, and p = 0.40,
P(8<X<12) = P(X=9)+P(X=10) + P(X=11)
= 0.0612+0.0245+0.0074
= 0.0931
Therefore,0.0931 is the probability that at least 10 pay in cash.
Learn more about probability
brainly.com/question/11234923
#SPJ4
What is the average rate of change for this exponential function for the interval from x = 2 to x = 4?

Answers
Answer:
The average rate of change over the interval is 120
Step-by-step explanation:
For a function f(x) the average rate of change over an interval [a,b] is given as;
f(b)-f(a)/b-a
in this case, a is 2 and b is 4
f(b) is 256 and f(a) is 16
Substituting these values in the equation for rate of change, we have;
(256-16)/(4-2) = 240/2 = 120
Find the scale factor

Answers
Answer:
3
Step-by-step explanation:
4*3=12
3*3=9
5*3=15
So you find the number that can be multiplied or divided by each side the same to get the new number
Explanation:
Focus on the horizontal sides. The jump from 3 to 9 is "times 3".
If you focus on the vertical sides, the jump from 4 to 12 is also "times 3".
Lastly, the slanted sides has a jump from 5 to 15 which is also "times 3".
This all shows the scale factor is 3. The larger triangle on the right has its sides 3 times as long compared to the smaller triangle.
Solve for x
y = a(z-h)² + k

Answers
Answer: The first answer.
Step-by-step explanation:
So, we want to isolate x.
First, subtract "k" from both sides.
Then, divide "a" on both sides.
Get rid of the squared on the right side by square rooting both sides.
Finally, add "h".
Based on these procedures, it is the first answer.
the epa recently strengthened the national ambient air quality standards for maximum daily concentration of pm2.5 from 65 micrograms to 35 micrograms. describe how this change will impact admission rates at medical facilities.
Answers
The strengthening of National Ambient Air Quality Standards for maximum daily concentration of PM2.5 from 65 micrograms to 35 micrograms is expected to have a positive impact on public health.
The PM2.5 is defined as a fine particulate matter which penetrate deep into the lungs and cause a range of health problems, including asthma attacks, heart disease, and lung cancer.
By lowering the maximum daily concentration of PM2.5, the EPA is aiming to reduce the amount of air-pollution that people are exposed to, which should lead to improvements in public health.
Therefore, the strengthening of the National Ambient Air Quality Standards for PM2.5 is a positive step towards protecting public health and reducing the burden on medical facilities.
Learn more about National Ambient Air Quality Standards here
https://brainly.com/question/5602732
#SPJ4
the contingency table below shows the blood types of a sample of people cross classified by sex. what percentage of the men in the sample have blood type o?
Answers
The percentage of the men in the sample who have blood type O is 40.38%.
What is the percentage?
A percentage is a figure or ratio stated as a fraction of 100 in mathematics. The acronyms pct., pct., and occasionally pc are also used to indicate it, however, the percent sign is most frequently used. A % is a number without dimensions and without a standard measurement.
Here, we have
Given: The contingency table below shows the blood types of a sample of people cross-classified by sex.
We have to find the percentage of the men in the sample who have blood type o.
Total number of males = 104
Number of males who has blood type O = 42
Percentage of the males in the sample have blood type O:
= (42×100%)/104
= 40.38%
Hence, the percentage of the men in the sample who have blood type O is 40.38%.
To learn more about the percentage from the given link
https://brainly.com/question/843074
#SPJ4
Find −1/4(−8.6) . Write your answer as a decimal to the nearest hundredth.
Answers
Answer:
2.15
Step-by-step explanation:
I will assume that "−1/4(−8.6)" is telling us to multiply (-8.6) times -(1/4):
(-1/4)*(-8.6)
= (8.6/4)
= 2.15
The difference of the same side interior angles of two parrelels lines is 50 degrees find all angles
Answers
Answer:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
Step-by-step explanation:
Angle 1: Same-side interior angle of Line 1
Angle 2: Same-side interior angle of Line 2
We know that the difference between the angles is 50 degrees. Since the angles are supplementary, we can write the equation:
Angle 1 + Angle 2 = 180
Now, we need to express the difference between the angles in terms of Angle 1 or Angle 2. We can choose either angle, so let's express it in terms of Angle 1:
Angle 1 - Angle 2 = 50
We can rewrite this equation as:
Angle 1 = 50 + Angle 2
Now substitute this expression for Angle 1 into the first equation:
(50 + Angle 2) + Angle 2 = 180
Combine like terms:
2Angle 2 + 50 = 180
Subtract 50 from both sides:
2Angle 2 = 130
Divide by 2:
Angle 2 = 65
Now substitute this value back into the equation for Angle 1:
Angle 1 = 50 + Angle 2
Angle 1 = 50 + 65
Angle 1 = 115
Therefore, the angles are as follows:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
sorry for all the screen wrinkles but what’s this

Answers
Answer:
cubic polynomial, monomial
Step-by-step explanation:
write the parametric equations of the line l passing through point a(5,-8,4) and perpendicular with the plane p described by the equation
Answers
The parametric equations of the line l passing through the given point and perpendicular with the plane p is x = 5 - 3t, y = -8 - 3t, and z = 4 - t.
To find the parametric equations of the line passing through point a (5,-8,4) and perpendicular to the plane p described by the equation 1x - 3y + 3z = 6, we need to first find the direction vector of the line.
The normal vector of the plane p is (1,-3,3), since the coefficients of x, y, and z in the plane equation represent the components of the normal vector.
To find the direction vector of the line, we take the cross product of the normal vector of the plane p and any vector that lies on the line. We can choose the vector (1,0,0) as lying on the line, since it is perpendicular to the normal vector of the plane.
Thus, the direction vector of the line is:
(1,0,0) x (1,-3,3) = (-3,-3,-1)
Now we can write the parametric equations of the line in vector form:
r = a + t*d
where r is the position vector of any point on the line, t is a parameter, a is the position vector of the known point on the line (5,-8,4), and d is the direction vector of the line (-3,-3,-1).
So the parametric equations of the line passing through point a (5,-8,4) and perpendicular to the plane p described by the equation 1x - 3y + 3z = 6 are:
x = 5 - 3t
y = -8 - 3t
z = 4 - t
Learn more about Parametric equations:
https://brainly.com/question/30451972
#SPJ11
What is the probability of drawing a diamond or a spade card from a standard deck of cards and rolling a 2 on a six-sided die?
10. 7%
25%
8. 3%
04. 2%
Answers
The probability of drawing a diamond or a spade card from a standard deck of cards and rolling a 2 on a six-sided die is 8.33%
To calculate the probability of drawing a diamond or a spade card from a standard deck of cards, we need to find the total number of diamond and spade cards in the deck. There are 13 cards in each suit, so there are 26 diamond and spade cards in total. The deck has 52 cards in total, so the probability of drawing a diamond or a spade card is:
P(diamond or spade) = 26/52 = 1/2 = 50%
To calculate the probability of rolling a 2 on a six-sided die, we need to find the total number of possible outcomes, which is 6 (since there are 6 sides on the die), and the number of favorable outcomes, which is 1 (since there is only one face with a 2 on it). Therefore, the probability of rolling a 2 on a six-sided die is:
P(rolling a 2) = 1/6 = 16.67%
To find the probability of both events happening together (drawing a diamond or a spade card and rolling a 2 on a six-sided die), we multiply the probabilities of each event:
P(diamond or spade AND rolling a 2) = P(diamond or spade) * P(rolling a 2)
= 50% * 16.67%
= 8.33%
To learn more about probability
https://brainly.com/question/24870672
#SPJ11
what is the probability of randomly selecting three americans from a group of 8 italians and 5 americans? enter your answer as a fraction.
Answers
The overall probability of selecting three Americans is:5/13 * 4/12 * 3/11 = 5/143 Answer: 5/143
Probability of selecting first American = number of Americans / total number of people= 5 / (5 + 8)= 5 / 13
Probability of selecting the second American = number of Americans / total number of remaining people after selecting the first American
= 4 / 12 (as there will be 12 people remaining after selecting the first American, which includes 4 Americans and 8 Italians)
Probability of selecting the third American = number of Americans / total number of remaining people after selecting the first and second American
= 3 / 11 (as there will be 11 people remaining after selecting the first and second American, which includes 3 Americans and 8 Italians)
Therefore, the overall probability of selecting three Americans is:5/13 * 4/12 * 3/11 = 5/143 Answer: 5/143
Know more about probability here:
https://brainly.com/question/251701
#SPJ11
Find the perimeter of the figure
where the length is 4x + 7,
the width is 2x - 5.
Answers
6x+2=0
x=-1/3
Now put the value of which is -1/3 in length and breadth .
I had done like this , May be it’s right or wrong ,
May be it might helps you!
What is the solution to the inequality 7x + 2 < -3x + 1?
Answers
10x +2 < 1
10x < -1
x < -1/10
I believe this is correct
Dominique is selling merchandise for a school fundraiser. she is selling calendars for $7 each and coffee mugs for $11 each. she must sell at least $700 of merchandise, including at least 50 mugs, to meet her goals. if x represents the number of calendars and y represents the number of mugs, which system of inequalities represents this scenario? 7x 11y > 700 and y > 50 7x 11y > 700 and x > 50 7x 11y ≥ 700 and y ≥ 50 7x 11y ≥ 700 and x ≥ 50
Answers
System of inequalities that represents this scenario is 7x + 11y ≥ 700 (the total amount of merchandise sold must be at least $700) y ≥ 50 (at least 50 coffee mugs must be sold)
Dominique is selling merchandise for a school fundraiser. To meet her goals, she must sell at least $700 worth of merchandise, including at least 50 coffee mugs.
Let x be the number of calendars sold and y be the number of coffee mugs sold. The revenue from selling x calendars and y coffee mugs can be calculated as follows:
Revenue = (Price per calendar) x (Number of calendars sold) + (Price per coffee mug) x (Number of coffee mugs sold)
Given that calendars are being sold for $7 each and coffee mugs are being sold for $11 each, the revenue equation can be expressed as:
Revenue = 7x + 11y
To meet the fundraising goal of selling at least $700 worth of merchandise, the total revenue generated from the sale of calendars and coffee mugs must be at least $700. Hence, we can express this as the inequality:
7x + 11y ≥ 700
In addition, Dominique must sell at least 50 coffee mugs. This can be expressed as the inequality:
y ≥ 50
Combining both inequalities, we get the system of inequalities:
7x + 11y ≥ 700 and y ≥ 50
This system of inequalities represents the scenario where Dominique must sell at least $700 worth of merchandise, including at least 50 coffee mugs. The first inequality ensures that the total revenue generated from the sale of calendars and coffee mugs meets the fundraising goal, while the second inequality ensures that at least 50 coffee mugs are sold.
To learn more about inequalities Click here:
brainly.com/question/30228778
#SPJ4
In a random sample of 74 homeowners in a city, 22 homeowners said they would
support a ban on nonnatural lawn fertilizers to protect fish in the local waterways. The sampling
method had a margin of error of ±3. 1%. SHOW ALL WORK!
A) Find the point estimate.
B) Find the lower and upper limits and state the interval
Answers
A) The point estimate for the proportion of all homeowners in the city who would support a ban on nonnatural lawn fertilizers is 0.297.
B) The 95% confidence interval for the proportion of all homeowners in the city who would support a ban on nonnatural lawn fertilizers is (0.266, 0.328).
A) The point estimate is the best estimate for the proportion of all homeowners in the city who would support a ban on nonnatural lawn fertilizers to protect fish in the local waterways. We can find this by taking the proportion of homeowners in the sample who said they would support a ban:
point estimate = x/n = 22/74 = 0.297
Therefore, the point estimate for the proportion of all homeowners in the city who would support a ban on nonnatural lawn fertilizers is 0.297.
B) The margin of error is ±3.1%. To find the lower and upper limits of the confidence interval, we can use the following formula:
lower limit = point estimate - margin of error
upper limit = point estimate + margin of error
Substituting the values we know, we get:
lower limit = 0.297 - 0.031 = 0.266
upper limit = 0.297 + 0.031 = 0.328
Therefore, the 95% confidence interval for the proportion of all homeowners in the city who would support a ban on nonnatural lawn fertilizers is (0.266, 0.328).
learn more about "Proportion":- https://brainly.com/question/1496357
#SPJ11
PLEASE HELP I'LL GIVE A BRAINLIEST PLEASE 30 POINTS!!! PLEASE I NEED A STEP BY STEP EXPLANATION PLEASE.

Answers
Answer:
(a) \(x=\frac{19}{4}=4.75\)
(b) \(x=-\frac{1+\sqrt{193}}{6}\approx-2.4821, x=-\frac{1-\sqrt{193}}{6}\approx2.1487\)
Step-by-step explanation:
The detailed explanation is shown in the attached documents below.

