Does the following infinite series converge or diverge? 1/3+2/9+4/27+8/81
Answers
Answer:
converge
Step-by-step explanation:
The ratio that you multiply by to get the next term is 2/3, which is less than 1, so the geometric series converges by the Geometric Series Test.
Answer:
Converge
Step-by-step explanation:
The value of r in this infinite series is 2/3.
If the absolute value of r is less than 1, then the infinite series converges.
Since 2/3 is less than 1, the series must converge.
Related Questions
If a United States dollar is worth $0.87 in European currency (euros), how much is $100 in Euros worth in United States money, to the nearest cent? Show ALL work and steps to get full credit!
Answers
The value of $100 in euros is $87.
What is ratio?Ratio basically compares quantities, that means it show value of one quantity with respect to other quantity.
If a and b are two values, their ratio will be a:b,
Given that,
Worth of 1 United States dollar is $0.87 in euros.
To find the value of $100 in Euros, use ratio property,
1 United States dollar = $0.87 in euros
100 United States dollar = $87 in euros.
The value of $100 in euros is $87.
To know more about Ratio on:
https://brainly.com/question/23724140
#SPJ1
the formulation for a linear programming problem cannot include more than one decision variable. group of answer choices true false
Answers
False. A linear programming problem can include more than one decision variable. Linear programming is a mathematical method used to find the optimal solution for a problem with multiple constraints and objectives, often related to maximizing or minimizing a certain value.
Decision variables are the variables that determine the potential solutions, and their values can be changed to affect the outcomes.
In many practical situations, there are multiple decision variables involved. For instance, a company may need to determine the optimal production quantities for different products, subject to resource constraints and market demands. In this case, the decision variables would represent the production quantities for each product, and there would be more than one variable.
In conclusion, the statement that a linear programming problem cannot include more than one decision variable is false. Multiple decision variables can be present in a linear programming formulation to address complex problems that involve multiple choices and constraints.
To learn more about linear programming : brainly.com/question/31758568
#SPJ11
Can someone please help me out with this question

Answers
Answer:
C.
Step-by-step explanation:
Dados los intervalos A=]-2;2[ ,B=[0;5[ y C=]-∞;1], determine el intervalo que resulta de operar: (A∩B)-C
Answers
Answer: ]1, 2[
Step-by-step explanation:
\(A \cap B=[0; 2[\\\\(A \cap B)-C=]1, 2[\)
What are the solutions to the equations below? answer in simpliest form
3(2w+6)-2=2(6w-8)+2w
4(x-1)=1/2(x-8)
4(x+3)-4=8(1/2x+1)
2(2x-5)+2x=7x-1
3x+7x+1=2(5x+1)
Answers
Step-by-step explanation:
6w+18-2=12w-16+2w
32=8w
-8w=-32
w=4
4x-4=1/2x-4
3 1/2x=0
x=0
4x+12-4=4x+8
0=0
4x-10+2x=7x-1
-3x=9
x=-3
3x+7x+1=10x+2
0=1 (undefined)
100-80 divided by 4+(6-3) using pemdas
Answers
Answer:88.57
Step-by-step explanation: If your doing PEMDAS you do () Wich is 6-3 and gives 3tyen you do Addition which is 4+3=7 Then do Subtraction which is 100-80 so the equation is 100-80/7=88.57 etc.
Determine the answer to (−5) + 4 and explain the steps using a number line.
Answers
Answer:
-1
Step-by-step explanation:
when adding on a number line you always go to the right.
-5+4=-1 , so you would move 4 places to the right on the number line.
-5+4
-1
is the correct answer
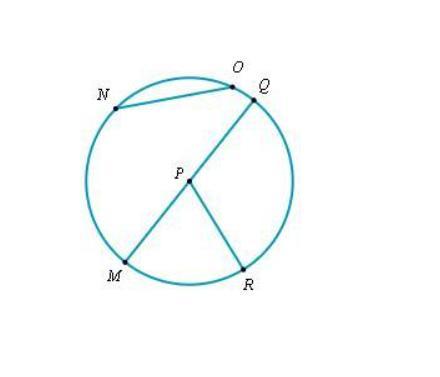
A circle with center is shown in the figure below.
S
T
W
R
U
V
(a) Name a radius:
(b) Name a diameter:
(c) Name a chord:
(d) If the length of is units,
what is the length of ?
Answers
The names of the radius , chord and diameter of a circle are as follow,
Radius of the circle are PQ, PM , And PR.
Diameter of the circle is QM
Chord of the circle is ON.
Length of QM in the circle = 4units.
In the attached figure of the circle,
Center of the circle is P.
radius of the circle is a distance from the center of the circle to its circumference.
Radius = PQ, PM , And PR.
Diameter of the circle passing through center P is QM.
Chord of the circle representing a line segment having endpoints on the circumference of the circle.
Chords are ON and MQ.
Diameter is the longest chord.
length of PR is 2 units,
PR is radius
QM is diameter
QM = 2(PR)
length of QM = 2(2)
= 4 units.
Therefore, for the given circle we have,
Radius are PQ, PM , And PR.
Diameter is QM
Chord is ON.
Length of QM = 4units.
learn more about circle here
brainly.com/question/28998766
#SPJ1
The above question is incomplete, the complete question is:
A circle with center P is shown in the figure below.
(a) Name a diameter:
(b) Name a radius:
(c) Name a chord:
(d) If the length of PR is 2 units, what is the length of QM
Attached figure.
Solve the System of equations -8x+3y= -17 and 3x-y=7 by combining the equations.

Answers
Answer: x = 1, y = -3
Step-by-step explanation: you're welcome :)
Answer:
the answer is (x,y) (4,5)
Please help me asap with this math problem!
If it's wrong I'ma report it!

Answers
Answer:
A) The correct inequality is: -18 < 53
B) The correct description is: Eduardo sent fewer text messages during May than April
Step-by-step explanation:
Month Number of message
April 53
May -18
A) The correct inequality is: -18 < 53
Reason:
We need to choose the correct inequality, negative number is less than positive number so the inequality will be -18 < 53
B) The correct description is: Eduardo sent fewer text messages during May than April
Reason:
Negative values shows that he has messaged under the allotted limit, while positive values shows the number of messages he was over the limit.
1. Find the value of X
2. Find the measure of RSM
3. Find the measure of PTU
4. List all the angles congruent to RSM
5. List all angles congruent to PTU

Answers
The value of X is 13 .
the measure of RSM is 99°.
the measure of PTU is 99 °.
The angles congruent to∠ RSM are ∠STP , ∠OTU and ∠NST.
The angles congruent to ∠PTU are ∠STQ , ∠RSN and ∠MST.
What are the properties of parallel lines?When two lines do not cross at any point in a plane, they are said to be parallel. A pair of lines that never cross paths and do not have a common junction point are said to be parallel. Parallel lines are represented by the symbol "||".
Any two parallel lines can be separated by a consistent amount of perpendicular space.
Lines that run parallel to one another do not intersect. Parallel lines intersect at infinity is another way of putting it.
Pairs of angles are created when a transversal connects two parallel lines, for example:
Corresponding anglesAlternate interior anglesAlternate exterior anglesVertically opposite anglesLinear pairTwo lines are said to cross at a point in a plane when they do so, which is referred to as an intersection of lines.
To know more about properties of parallel lines ,visit:
brainly.com/question/28646177
#SPJ13
Sixteen times a number x is less than -2.
Answers
Answer:
16x<-2
Step-by-step explanation:
Choose all true statements.
All real numbers are rational numbers.
Some rational numbers are natural numbers.
No real numbers are irrational numbers.
All whole numbers are integers.
Some integers are natural numbers.
No rational numbers are integers.
Answers
Answer:
- All real numbers are rational numbers. FALSE
- Some rational numbers are natural numbers. TRUE
- No real numbers are irrational numbers. FALSE
- All whole numbers are integers. TRUE
- Some integers are natural numbers. TRUE
- No rational numbers are integers. FALSE
Answer: B,D, and E
Step-by-step explanation:
A. All real numbers are rational numbers.
B. Some rational numbers are natural numbers
C.No real numbers are irrational numbers.
D.All whole numbers are integers.
E. Some integers are natural numbers.
F. No rational numbers are integers.
write 1042000 000 m+ in scientific notification
Answers
Answer:
1.042 × 109
Step-by-step explanation:
you have to move the decimal from the zero.
C
\qquad m \angle AOC
m∠AOC
m, angle, A, O, C
is a straight angle.
m
∠
A
O
B
=
8
x
+
5
1
∘
\qquad m \angle AOB = 8x + 51^\circ
m∠AOB=8x+51
∘
m, angle, A, O, B, equals, 8, x, plus, 51, degrees
m
∠
B
O
C
=
6
x
−
2
5
∘
\qquad m \angle BOC = 6x - 25^\circ
m∠BOC=6x−25
∘
m, angle, B, O, C, equals, 6, x, minus, 25, degrees
Find
m
∠
A
O
B
m\angle AOB
m∠AOB
m, angle, A, O, B
:

Answers
Answer:
m∠AOB=139°Step-by-step explanation:
m∠AOB+m∠BOC=180°
m∠AOB=8x+51°
m∠BOC=6x-25°
~
\(\tt 8x+51+6x-25=180\)
\(\tt 14x+26=180\)
\(\tt 14x=180-26\)
\(\tt \cfrac{14x}{14} =\cfrac{154}{14}\)
\(\tt x=11\)
m∠AOB:-
\(\tt 8(11)+51\)
\(\tt =88+51\)
\(\tt =139^{o}\)
Therefore, m∠AOB=139°
Is this is it rational or irrational? If rational prove it by converting it to a fraction
Answers
Answer:18
Step-by-step explanation:trust
Find the generating function of the sequence {an}n≥0 determined by an = an−1 + 6an−1 with initial conditions a0 = 1, a1 = 3. You need to find the closed form of the generating function, but you don’t need find the closed form of the coefficients.
Answers
The generating function for the sequence {an} is given by a(x) = (1 + 2x) / (1 - x - 6x^2). It captures the terms of the sequence {an} as coefficients of the powers of x.
To find the generating function of the sequence {an}, we can use the properties of generating functions and solve the given recurrence relation.
The given recurrence relation is: an = an-1 + 6an-2
We are also given the initial conditions: a0 = 1 and a1 = 3.
To find the generating function, we define the generating function A(x) as:
a(x) = a0 + a1x + a2x² + a3x³ + ...
Multiplying the recurrence relation by x^n and summing over all values of n, we get:
∑(an × xⁿ) = ∑(an-1 × xⁿ) + 6∑(an-2 × xⁿ)
Now, let's express each summation in terms of the generating function a(x):
a(x) - a0 - a1x = x(A(x) - a0) + 6x²ᵃ⁽ˣ⁾
Simplifying and rearranging the terms, we have:
a(x)(1 - x - 6x²) = a0 + (a1 - a0)x
Using the given initial conditions, we have:
a(x)(1 - x - 6x²) = 1 + 2x
Now, we can solve for A(x) by dividing both sides by (1 - x - 6x^2²):
a(x) = (1 + 2x) / (1 - x - 6x²)
Therefore, the generating function for the given sequence is a(x) = (1 + 2x) / (1 - x - 6x²).
Read more on Functions here: https://brainly.com/question/29890699
#SPJ11
please answer with working
= (10 points) Solve for t given 2. 7 = 1.0154. Tip: take logs of both sides, apply a rule of logs then solve for t.
Answers
Solving the equation 2.7 = 1.0154 gives t ≈ 8.871.
To solve for t given the equation 2.7 = 1.0154, we can follow these steps:
Take the logarithm of both sides of the equation. Since the base of the logarithm is not specified, we can choose any base. Let's use the natural logarithm (ln) for this example:
ln(2.7) = ln(1.0154)
Apply the logarithmic rule: ln(a^b) = b * ln(a). In this case, we have:
ln(2.7) = t * ln(1.0154)
Solve for t by isolating it on one side of the equation. Divide both sides of the equation by ln(1.0154):
t = ln(2.7) / ln(1.0154)
Calculate the value of t using a calculator or mathematical software:
t ≈ 8.871
Therefore, solving the equation 2.7 = 1.0154 gives t ≈ 8.871.
To know more about logarithm ,visit:
https://brainly.com/question/16529257
#SPJ11
Question 15
Fill-in-the-blank Question
Carl filled 12 mugs with coffee. Each mug has 250 mL of coffee.
How many liters of coffee did Carl use in all?
Answers
Answer:
Carl used a total of 3 liters of coffee in all.
Step-by-step explanation:
There are 1000 milliliters (mL) in a liter, so to convert from milliliters to liters, you need to divide by 1000.
To find the total amount of coffee used, you can multiply the number of mugs by the volume of each mug:
12 mugs x 250 mL/mug = 3000 mL
To convert this to liters, you divide by 1000:
3000 mL ÷ 1000 = 3 L
Therefore, Carl used 3 liters of coffee in all.
Answer:
Carl used 3 liters of coffee in all
Step-by-step explanation:
Step 1: multiply 12 by 250 to determine how mL are in all the mugs of coffee which gets you 3000
Step 2 convert: There are 1000 milliliters (mL) in a liter, so to convert from milliliters to liters, you need to divide by 1000. So divide 3000 by 1000 to find how much liters Carl uses in all. Which gets you 3
Therefore, Carl used 3 liters of coffee in all
Evaluate 64^1/2 x 10^-2
Answers
0.32 is the answer to 64^1/2 x 10^-2
Line Integrals over Plane Curves 19. Evaluate fex ds, where C is a. the straight-line segment x = 1, y = 1/2, from (0, 0) to (4,2). b. the parabolic curve x = 1, y = 1², from (0, 0) to (2, 4).
Answers
In the given problem, we are required to evaluate the line integral ∫(C) fex ds, where f(x, y) = ex and C represents a curve in the xy-plane. We need to evaluate the integral for two different cases: (a) for the straight-line segment from (0, 0) to (4, 2) and (b) for the parabolic curve from (0, 0) to (2, 4).
(a) For the straight-line segment, we have x = 1 and y = 1/2. The parameterization of the curve can be written as x(t) = t and y(t) = t/2, where t varies from 0 to 4. Using this parameterization, we can express ds in terms of dt as ds = √(dx/dt² + dy/dt²) dt = √(1² + (1/2)²) dt = √(5)/2 dt. Therefore, the line integral becomes ∫(C) fex ds = ∫(0 to 4) (\(e^t\))(√(5)/2) dt. This integral can be evaluated using standard techniques of integration.
(b) For the parabolic curve, we have x = 1 and y = t². The parameterization of the curve can be written as x(t) = 1 and y(t) = t², where t varies from 0 to 2. Using this parameterization, we can express ds in terms of dt as ds = √(dx/dt² + dy/dt²) dt = √(0² + (2t)²) dt = 2t dt. Therefore, the line integral becomes ∫(C) fex ds = ∫(0 to 2) (e)(2t) dt. Again, this integral can be evaluated using standard integration techniques.
In summary, to evaluate the line integral ∫(C) fex ds for the given curves, we need to parameterize the curves and express ds in terms of the parameter. Then we can substitute these expressions into the line integral formula and evaluate the resulting integral using integration techniques.
Learn more about integral here: https://brainly.com/question/31059545
#SPJ11
given the finite sequence x[n] = {1 3 6}, starts at n = 0. show how you could find the sum (i.e.,10) using the integrator/accumulator function in the z-domain.
Answers
To find the sum of a finite sequence using the integrator/accumulator function in the z-domain, we can follow these steps:
1. Given the finite sequence x[n] = {1, 3, 6}, where n starts at 0.
2. We need to convert the sequence from the time domain to the z-domain. In the z-domain, the sequence will be represented by a z-transform.
3. The z-transform of a sequence x[n] is defined as X(z) = Σ(x[n] * z^(-n)), where Σ represents the summation from n = -∞ to n = ∞.
4. In our case, the sequence x[n] starts at n = 0. Therefore, we need to rewrite the z-transform formula by shifting the index appropriately.
5. Shifting the index by k = 0, we have X(z) = Σ(x[n] * z^(-n)) = Σ(x[k] * z^(-k)), where Σ represents the summation from k = 0 to k = ∞.
6. Plugging in the values of the sequence x[k] = {1, 3, 6}, we have X(z) = 1 * z^0 + 3 * z^(-1) + 6 * z^(-2).
7. To find the sum of the sequence, we need to evaluate the z-transform at z = 1. In other words, we substitute z = 1 in X(z).
8. Evaluating X(z) at z = 1, we have X(1) = 1 * 1^0 + 3 * 1^(-1) + 6 * 1^(-2).
9. Simplifying the expression, we get X(1) = 1 + 3 + 6 = 10.
10. Therefore, the sum of the given finite sequence x[n] = {1, 3, 6} is 10 when evaluated using the integrator/accumulator function in the z-domain.
#SPJ11
Learn more about Domain : https://brainly.com/question/2264373
Slope intercept equation

Answers
What is “x”?? Plz help me

Answers
in a small metropolitan area, annual claims due to storm and fire are independently distributed random variables. the probability of having a claim due to storm is x in the first year and it increases by 20% each year thereafter. the probability of having a claim due to fire is y in the first year and it decreases by 15% each year thereafter. the increases and decreases each year are compounded, and are in effect for between seven and ten years. the probability of having a claim due to storm and fire in the second year is 0.157. calculate the probability of having a claim due to storm and fire in the seventh year.
Answers
The probability of having a claim due to storm and fire in the seventh year is 0.090, assuming the increases and decreases in probabilities are compounded and remain in effect for seven years.
Let's break down the problem step by step. We are given that the probability of having a claim due to storm in the first year is x, and it increases by 20% each subsequent year. Therefore, the probability of having a claim due to storm in the second year is 1.2x (20% increase).
Similarly, the probability of having a claim due to fire in the first year is y, and it decreases by 15% each subsequent year. Thus, the probability of having a claim due to fire in the second year is 0.85y (15% decrease).
The probability of having a claim due to both storm and fire in the second year is given as 0.157. Since these events are independent, we can multiply the probabilities of each event to get the joint probability. Therefore, we have (1.2x) * (0.85y) = 0.157.
Solving this equation gives us xy = 0.1645.
Now, we need to calculate the probability of having a claim due to storm and fire in the seventh year. Using the given information that the increases and decreases in probabilities remain in effect for between seven and ten years, we assume that the probabilities remain constant for seven years.
Hence, the probability of having a claim due to storm and fire in the seventh year is (1.2^6x) * (0.85^6y) = 0.090.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
The wall is to be 5ft by 7 ft. A brick is 4 inches by 12 inches. How many bricks are needed
Answers
ok
Dimensions = 5 ft x 7 ft
Brick = 4 in x 12 in
1.- Convert ft to in
1 ft -------------------- 12 in
5 ft ------------------- x
x = (5 x 12) / 1
x = 60 in
1 ft -------------------- 12 in
7 ft -------------------- x
x = (7 x 12) / 1
x = 84 in
2.- Calculate the area of the wall
Area = 60 x 84
= 5040 in^2
3.- Calculate the area of a brick
Area = 4 x 12 = 48 in^2
4.- Divide the area of the wall by the area of the brick
Number of bricks = 5040 / 48
= 105
There will be 105 brick on the wall.
Connor has made deposits of $125.00 into his savings account at the end of every three months for 15 years. If interest is 10% per annum compounded monthly and he leaves the accumulated balance for another 5 years, what would be the balance in his account then?
Answers
You can calculate the balance in Connor's account after 15 years of regular deposits and an additional 5 years of accumulation.
To calculate the balance in Connor's account after 15 years of regular deposits and an additional 5 years of accumulation with 10% interest compounded monthly, we can break down the problem into two parts:
Calculate the accumulated balance after 15 years of regular deposits:
We can use the formula for the future value of a regular deposit:
FV = P * ((1 + r/n)^(nt) - 1) / (r/n)
where:
FV is the future value (accumulated balance)
P is the regular deposit amount
r is the interest rate per period (10% per annum in this case)
n is the number of compounding periods per year (12 for monthly compounding)
t is the number of years
P = $125.00 (regular deposit amount)
r = 10% = 0.10 (interest rate per period)
n = 12 (number of compounding periods per year)
t = 15 (number of years)
Plugging the values into the formula:
FV = $125 * ((1 + 0.10/12)^(12*15) - 1) / (0.10/12)
Calculating the expression on the right-hand side gives us the accumulated balance after 15 years of regular deposits.
Calculate the balance after an additional 5 years of accumulation:
To calculate the balance after 5 years of accumulation with monthly compounding, we can use the compound interest formula:
FV = P * (1 + r/n)^(nt)
where:
FV is the future value (balance after accumulation)
P is the initial principal (accumulated balance after 15 years)
r is the interest rate per period (10% per annum in this case)
n is the number of compounding periods per year (12 for monthly compounding)
t is the number of years
Given the accumulated balance after 15 years from the previous calculation, we can plug in the values:
P = (accumulated balance after 15 years)
r = 10% = 0.10 (interest rate per period)
n = 12 (number of compounding periods per year)
t = 5 (number of years)
Plugging the values into the formula, we can calculate the balance after an additional 5 years of accumulation.
By following these steps, you can calculate the balance in Connor's account after 15 years of regular deposits and an additional 5 years of accumulation.
Learn more about balance from
https://brainly.com/question/28767731
#SPJ11
Convert the following decimal into a fraction.
0.83
Answers
Answer:
83/100
Step-by-step explanation:
To turn a decimal into a fraction, place decimal number over its place value.
Place value = 100
Decimal number = 83
The sum of two numbers is 106. The bigger number is 22 more than the smaller number. Then what is half of the smaller number?
(1 Point)
a) 84
b) 21
c) 42
d) 32
7Rakesh's mother's age is three times the present age of Rakesh. After 5 years their ages when added together, will become 66 years. The equation that represents the above is as follows;
(1 Point)
a) x + 3x = 66
b) x + 3x + 5 = 66
c) 4x + 15 = 66
d) 4x + 10 = 66
8Equation 1 is : 2 x - 3 = - 9 and Equation 2 is : x - 7 = 2. The first equation has solution (x = - 3), and the second equation has solution (x = 9) and both these answers are correct for the respective equations. Choose the correct statement from below.
(1 Point)
a) Since the first equation has a negative solution, the second equation only is a Linear equation, as it has a positive solution
b) Both equations have solutions which are rational numbers
c) The first equation is called a Negative Linear Equation as it has a negative solution
d) None of the statements a, b or c are True
9Please see the Figure A, and choose the correct
statement that matches the figure from the
options given below.
(1 Point)
a) The above figure is a Polygon with 5 sides
b) The above figure is a Concave Polygon
c) The above figure is not a Polygon
d) The above figure is a Regular Pentagon
10The sum of measures of the exterior angles of any polygon is …
(1 Point)
a) 180 degrees
b) 360 degrees
c) ( n – 2 ) x 180 degrees
d) ( n – 2 ) x 360 degrees
11In a quadrilateral, if all sides are equal and the diagonals bisect each other at right angles, then the quadrilateral …
(1 Point)
a) Is a Square
b) Is a Rhombus
c) Could be a Square, or could be a Rhombus, we need to know more about the length of the diagonals
d) None of the above statements is correct
12A rectangular wire frame could be bent and turned into a Parallelogram keeping the same 4 original sides, but the following must be true for this to happen…..
(1 Point)
a) That the diagonals remain equal
b) That the diagonals continue to bisect the angles at the vertices equally
c) The lengths of the diagonals change
d) The diagonals are now bisecting each other in 4 equal parts
13Which statement is True for the following two Figures A and B, given below
(1 Point)
a) Figure A is a Rhombus and Figure B is a Kite
b) Figure A and B are both Rhombus
c) Figure A and B are both Kites
d) Figure A is a Kite and Figure B is a Rhombus
14Which statement out of the four options below, is True?
(1 Point)
a) All Rectangles are Squares
b) All Rhombuses are Parallelograms
c) All Squares are Concave Polygons
d) All Convex Polygons have diagonals outside them
15
(1 Point)
16If 4368 ÷ 28 = 156, then if the same 4368 is now divided by 0.28, what will be the answer?
(1 Point)
a) 156
b) 15600
c) 15.6
d) 1.56
1712.00001 ÷ 0.600001 is closest to ……..
(1 Point)
a) 0.02
b) 2
c) 20
d) 200
18Complete:
(1 Point)
19The equation : 12 x + 16 = 20 is the same as ……
(1 Point)
a) 12 x + 8 = 12
b) 12 x = 20 + 16
c) 12 x – 16 = 20 – 16
d) 12 x – 20 = 16
2020. Find the value of a quarter of the angle QRT
which is ‘x’ if angle PRS is 2x as shown in the
figure below. Consider Triangle PRQ and Triangle
RST to be equilateral triangles of different sizes.
(1 Point)
21Which number will give us a quotient of - 4, if we divide - 24 by ……..
(1 Point)
a) 4
b) - 6
c) - 4
d) 6
22If 2 ( 3 – 2 x ) = 3 ( x – 5 ) then x = ……….
(1 Point)
a) – 3
b) 3
c) – 6
d) 6
23The teacher asked the class to divide a given number by 24
- Rohit divided the number by 24 and got the correct answer 20
- Mohit divided the number by 6 and got an answer which he again divided by 4 and
obtained the final answer
- Rakesh divided the number by 2.4 and then divided the answer again by 10
- Allen divided the number by 2.4 and then multiplied the answer obtained by 10
Now choose the best solution from the below options.
(1 Point)
a) Only Rohit got the correct answer
b) Both Rohit and Mohit got the correct answer
c) Rohit, Mohit and Rakesh all got the correct answer
d) Rohit, Mohit and Allen all got the correct answer
24Abhay and Binu both started walking starting at the same time and at the same rate of 5 km / hour. Abhay walked on the boundary of a big circle and Binu walked on the boundary of a small circle and both these circles were having the same center. Abhay completed 3 circles, whereas Binu completed 7 circles after half an hour. After half an hour …...................
(1 Point)
a) Abhay has walked more than Binu, as he walked on the boundary of the bigger circle
b) Binu has walked more than Abhay, as he has walked more circles than Abhay
c) Both of them have covered the same distance
d) With the information given above, we cannot say who walked more
25Which sign will you put in between [ 120 ….. ( 3 / 11 ) ], so that the answer or result is the highest number
(1 Point)
a) +
b) –
c) x
d) ÷
Answers
Step-by-step explanation:
on the first one you would take 106 and subtract 22 from that since the bigger number is 22 more than the smaller number 106 - 22=84 then you would divide that by two because there are two numbers. which would be 42 as a smaller number so half of the smaller number would be 21. I think
To solve the above, the solutions are given below.
1. b) 21
7. b) x + 3x + 5 = 66
8. b) Both equations have solutions which are rational numbers
9. a) The above figure is a Polygon with 5 sides
10. b) 360 degrees
11. In a quadrilateral, if all sides are equal and the diagonals bisect each other at right angles, then the quadrilateral …
a) Is a Square
12. A rectangular wire frame could be bent and turned into a Parallelogram keeping the same 4 original sides, but the following must be true for this to happen…..
b) That the diagonals continue to bisect the angles at the vertices equally
13. Which statement is True for the following two Figures A and B, given below
b) Figure A and B are both Rhombus
14Which statement out of the four options below, is True?
b) All Rhombuses are Parallelograms
16. If 4368 ÷ 28 = 156, then if the same 4368 is now divided by 0.28, what will be the answer?
b) 15600
17. 12.00001 ÷ 0.600001 is closest to ……..
c) 20
19. The equation : 12 x + 16 = 20 is the same as ……
a) 12 x + 8 = 12
20. Find the value of a quarter of the angle QRT
which is ‘x’ if angle PRS is 2x as shown in the
figure below. Consider Triangle PRQ and Triangle
RST to be equilateral triangles of different sizes.
80°
21. Which number will give us a quotient of - 4, if we divide - 24 by ……..
d) 6
22. If 2 ( 3 – 2 x ) = 3 ( x – 5 ) then x = ……….
b) 3
23. The teacher asked the class to divide a given number by 24
- Rohit divided the number by 24 and got the correct answer 20
- Mohit divided the number by 6 and got an answer which he again divided by 4 and
obtained the final answer
- Rakesh divided the number by 2.4 and then divided the answer again by 10
- Allen divided the number by 2.4 and then multiplied the answer obtained by 10
Now choose the best solution from the below options.
a) Only Rohit got the correct answer
24. Abhay and Binu both started walking starting at the same time and at the same rate of 5 km / hour. Abhay walked on the boundary of a big circle and Binu walked on the boundary of a small circle and both these circles were having the same center. Abhay completed 3 circles, whereas Binu completed 7 circles after half an hour. After half an hour …...................
c) Both of them have covered the same distance
25. Which sign will you put in between [ 120 ….. ( 3 / 11 ) ], so that the answer or result is the highest number
c) x
Therefore, the answers are as given above.
learn more about factorization from here: https://brainly.com/question/25829061
Consider a competitive market where there are two types of firms, Type A and Type B, with total cost functions TC4(q) = 1+2q+q? TCB(q) = 6 + 2q +3q2 (a) Derive the short-run supply curve for each firm type (b) What is the short-run market supply, if there are 10 Type A firms, and 6 Type B firms? (c) What is total quantity produced when p=5? (d) How does your answer at (c) change if we consider long run supply rather than short run? Here, assume again that p=5 and that there are 10 Type A firms and 6 Type B firms.
Answers
The total quantity produced when p = 5 is 26 in the long run.
In the short run, each firm will produce where its marginal cost equals the market price, which we'll denote as p.
So, for Type A firms, the short-run supply curve is:
q4(p) = (p-2)/2
And for Type B firms, the short-run supply curve is:
qB(p) = (p-2)/6
The short-run market supply is simply the sum of the quantities supplied by each type of firm at a given price level. So, if there are 10 Type A firms and 6 Type B firms, the short-run market supply at a price level of p is:
Qs(p) = 10q4(p) + 6qB(p)
= 10(p-2)/2 + 6(p-2)/6
= 8p - 20
The total quantity produced when p=5, we can substitute p=5 into the market supply equation we just derived:
Qs(5) = 8(5) - 20
= 20
So, the total quantity produced when p=5 is 20.
The long run, firms can enter or exit the market, and as a result, the number of firms in each market may change.
In this case, we'll assume that the number of Type A and Type B firms can adjust freely in the long run, and that each firm earns zero economic profit in the long run.
If there are zero economic profits, each firm's total revenue (TR) must equal its total cost (TC), which means that price must equal average total cost (ATC).
For Type A firms, ATC4(q) = TC4(q)/q = 1/q + 2 + q, so:
5 = 1/q + 2 + q
Rearranging and solving for q, we get:
q4 = 2
So each Type A firm will produce 2 units of output in the long run.
For Type B firms, ATCB(q) = TCB(q)/q = 6/q + 2 + 3q, so:
5 = 6/q + 2 + 3q
Rearranging and solving for q, we get:
qB = 1
So each Type B firm will produce 1 unit of output in the long run.
If there are 10 Type A firms and 6 Type B firms, the total quantity produced in the long run when p=5 is:
Qlr = 10q4 + 6qB
= 10(2) + 6(1)
= 26
So, the total quantity produced when p = 5 is 26 in the long run.
For similar question on quantity produced:
https://brainly.com/question/14039381
#SPJ11