Answers
Answer: 51
Step-by-step explanation:
We will use the Order of Operations, sometimes known as PEMDAS.
Given:
5x² - x + 9
Plug in the value of 3:
5(3)² - (3) + 9
To the power of 2:
5(9) - 3 + 9
Multiply:
45 - 3 + 9
Subtract:
42 + 9
Add:
51

Related Questions
A large part of the answer has to do with trucks and the people who drive them. Trucks come in all different sizes depending on what they need to carry. Some larger trucks are known as 18-wheelers, semis, or tractor trailers. These trucks are generally about 53 feet long and a little more than 13 feet tall. They can carry up to 80,000 pounds, which is about as much as 25 average-sized cars. They can carry all sorts of items overlong distances. Some trucks have refrigerators or freezers to keep food cold. Other trucks are smaller. Box trucks and vans, for example, hold fewer items. They are often used to carry items over shorter distances.
A lot of planning goes into package delivery services. Suppose you are asked to analyze the transport of boxed packages in a new truck. Each of these new trucks measures12 feet × 6 feet × 8 feet. Boxes are cubed-shaped with sides of either1 foot, 2 feet, or 3 feet. You are paid $5 to transport a 1-foot box, $25 to transport a 2-foot box, and $100 to transport a 3-foot box.
How many boxes fill a truck when only one type of box is used?
What combination of box types will result in the highest payment for one truckload?
Answers
A truck can carry either 576 1-foot boxes, 72 2-foot boxes, or 21 3-foot boxes.
The combination of boxes that will result in the highest payment for one truckload is 89 1-foot boxes, 3 2-foot boxes, and 3 3-foot boxes, for a total payment of $3,422.
How to determine volume?To find how many boxes of one type will fill a truck, calculate the volume of the truck and divide it by the volume of one box.
Volume of the truck = 12 ft × 6 ft × 8 ft = 576 cubic feet
Volume of a 1-foot box = 1 ft × 1 ft × 1 ft = 1 cubic foot
Number of 1-foot boxes that will fill the truck = 576 cubic feet / 1 cubic foot = 576 boxes
Volume of a 2-foot box = 2 ft × 2 ft × 2 ft = 8 cubic feet
Number of 2-foot boxes that will fill the truck = 576 cubic feet / 8 cubic feet = 72 boxes
Volume of a 3-foot box = 3 ft × 3 ft × 3 ft = 27 cubic feet
Number of 3-foot boxes that will fill the truck = 576 cubic feet / 27 cubic feet = 21.33 boxes (rounded down to 21 boxes)
Therefore, a truck can carry either 576 1-foot boxes, 72 2-foot boxes, or 21 3-foot boxes.
To determine the combination of box types that will result in the highest payment for one truckload, calculate the total payment for each combination of box types.
Let x be the number of 1-foot boxes, y be the number of 2-foot boxes, and z be the number of 3-foot boxes in one truckload.
The volume of the boxes in one truckload is:
V = x(1 ft)³ + y(2 ft)³ + z(3 ft)³
V = x + 8y + 27z
The payment for one truckload is:
P = 5x + 25y + 100z
To maximize P subject to the constraint that the volume of the boxes does not exceed the volume of the truck:
x + 8y + 27z ≤ 576
Use the method of Lagrange multipliers to solve this optimization problem:
L(x, y, z, λ) = P - λ(V - 576)
L(x, y, z, λ) = 5x + 25y + 100z - λ(x + 8y + 27z - 576)
Taking partial derivatives and setting them equal to zero:
∂L/∂x = 5 - λ = 0
∂L/∂y = 25 - 8λ = 0
∂L/∂z = 100 - 27λ = 0
∂L/∂λ = x + 8y + 27z - 576 = 0
From the first equation, we get λ = 5.
Substituting into the second and third equations, y = 25/8 and z = 100/27. Since x + 8y + 27z = 576, x = 268/3.
Round these values to the nearest integer because no fraction for a box. Rounding down, x = 89, y = 3, and z = 3.
Therefore, the combination of boxes that will result in the highest payment for one truckload is 89 1-foot boxes, 3 2-foot boxes, and 3 3-foot boxes, for a total payment of $3,422.
Find out more on volume here: https://brainly.com/question/27710307
#SPJ1
ANSWER THIS QUICK!! IT¨S WORTH 46 POINTS

Answers
Answer:
The answer is option AStep-by-step explanation:
\( \frac{4\pi \sqrt{5} - 2\pi \sqrt{5} }{3 \sqrt{5} } \)Simplify the numerator first
Since they have the same square root that's root 5 we can subtract them directly
That's
\(4\pi \sqrt{5} - 2\pi \sqrt{5} = (4\pi - 2\pi) \sqrt{5} \\ = 2\pi \sqrt{5} \)So we have
\( \frac{2\pi \sqrt{5} }{ 3\sqrt{5} } \)Reduce the expression with √5
We have the final answer as
\( \frac{2\pi}{3} \)Hope this helps you
how many four letter strings can be formed from the letters a,b,c,d,e if the first letter must be a vowel and the last letter must be a consonant?
Answers
Number of ways to form four letters strings formed using a, b, c, d, e with the given conditions is equal to 150ways.
As given in the question,
Given letters are a, b, c, d, e has
Number of vowel = 2
Number of consonant= 3
Number of letter strings to be formed = 4
Condition:
First letter must be vowel
Last letter must be consonant
First place filled in 2 ways
Second and Third place filled in 5ways
Last place filled in 3 ways
Total number of ways to form four letters strings
= 2 × 5 × 5 × 3
= 150
Therefore, number of ways to form four letter string is 150 ways.
Learn more about number of ways here
brainly.com/question/29110744
#SPJ4
Help me please.
create a function or equation shown in the graph

Answers
An equation for the function graphed above is \(y = \frac{12(x - 1)}{(x + 3)(x - 4)}\).
What is a vertical asymptote?In Mathematics and Geometry, the vertical asymptote of a function simply refers to the value of x (x-value) which makes its denominator equal to zero (0).
By critically observing the graph of the rational function shown above, we can logically deduce that its vertical asymptotes include the following;
x = -3 ⇒ x + 3 = 0.
x = 4 ⇒ x - 4 = 0.
In this context, an equation that represent its denominator is given by the following quadratic function:
Q(x) = (x + 3)(x - 4)
Assuming the leading coefficient of the function P(x) is represented by a;
P(x) = a(x - 1)
By evaluating and solving for the leading coefficient "a" in this function, we have;
f(x) = P(x)/Q(x)
f(x) = a(x - 1)/[(x + 3)(x - 4)]
f(0) = a(0 - 1)/[(0 + 3)(0 - 4)]
f(0) = -a/[(3)(-4)]
f(0) = a/12
Since the y-intercept of this graph is located at (0, 1), the value of the leading coefficient (a) is given by;
1 = a/12
1 = a/12
a = 12 × 1
a = 12
By substituting the value of the leading coefficient (a) into the function, we have the following;
f(x) = P(x)/Q(x)
f(x) = y = 12(x - 1)/[(x + 3)(x - 4)]
\(f(x) = y = \frac{12(x - 1)}{(x + 3)(x - 4)}\)
Read more on vertical asymptotes and functions here: https://brainly.com/question/28184937
#SPJ1
pls help if you can asap!!!!

Answers
Answer: x= 6
Step-by-step explanation:
Since the shape is a parallelogram, the angles will either be equal to each other or add up to 180.
You can see they do not look the same so they add up to equal 180
12x + 3 +105 = 180
12x + 108 = 180
12x = 72
x = 6
Factor the polynomial expression 8x^3-1
Answers
Answer:
Step-by-step explanation:

What is the solution of the system of equations below?
x + 3y = 7
2x - y = 7
Answers
Answer:
y = 1
x = 4
Step-by-step explanation:
x + 3y = 7 → ( 1 )
2x - y = 7 → ( 2 )
First, let us make x the subject in equation ( 1 ).
x = 7 - 3y → ( 3 )
Let us find the value of y.
For that let us take equation (1) & replace x with ( 7 - 3y ).
2x - y = 7
2 ( 7 - 3y ) - y = 7
Solve the brackets.
14 - 6y - y = 7
Combine like terms.
14 - 7y = 7
Subtract 14 from both sides.
-7y = 7 - 14
-7y = -7
Divide both sides by -7.
y = 1
Let us find value of x
For that let us take equation (3) & replace y with 1.
x = 7 - 3y
x = 7 - 3 × 1
x = 7 - 3
x = 4
If consumption is $5 billion when disposable income is $0 and if the marginal propensity to consume is dc 1 W +0.1 (in billions of dollars dy √y +1 find the national consumption function. C(y) =
Answers
Adding the initial consumption value of $5 billion, the national consumption function is: C(y) = 2√(y+1) + 5 (in billions of dollars)
To find the national consumption function C(y), we need to integrate the marginal propensity to consume (MPC) with respect to disposable income (y) and add the initial consumption value.
Given that the marginal propensity to consume is given by: dc/dy = 1/√(y+1)
We integrate dc/dy with respect to y:
∫(dc/dy) dy = ∫(1/√(y+1)) dy
Using the substitution u = y+1, du = dy, the integral becomes:
∫(1/√u) du
Applying the power rule of integration, we get:
2√u + C
Replacing u with y+1, we have:
2√(y+1) + C
Know more about consumption function here:
https://brainly.com/question/28145438
#SPJ11
In 1912, the RMS Titanic, a British passenger ship, sank in the North Atlantic Ocean after colliding with an iceberg. Historians do not know the exact passenger list, so the death toll is estimated. Here is data from the 2201 passengers on board, by cabin class.
First Class Second Class Third Class Crew Row totals
Died 122 167 528 673 1490
Survived 203 118 178 212 711
Column Totals 325 285 706 885 2201
Wikipedia, RMS Titanic. (2015). Retrieved from: http://en.wikipedia.org/wiki/RMS_Titanic#Survivors_and_victims
Which proportions are most useful in analyzing the relationship between passenger class and surviving the Titanic?
· 122 / 325 and 203 / 325
· 203 / 325 and 528 / 706
· 203 / 325 and 178 /706
· 203 / 711 and 178 / 711
In 1912, the RMS Titanic, a British passenger ship, sank in the North Atlantic Ocean after colliding with an iceberg. Historians do not know the exact passenger list, so the death toll is estimated. Here is data from the 2201 passengers on board, by cabin class. First Class Second Class Third Class Crew Row totals Died 122 167 528 673 1490 Survived 203 118 178 212 711 Column Totals 325 285 706 885 2201 Wikipedia, RMS Titanic. (2015). Which proportions are most useful in analyzing the relationship between passenger class and surviving the Titanic? • 122 / 325 and 203 / 325 • 203 / 325 and 528 / 706 • 203 / 325 and 178 /706 • 203 / 711 and 178 / 711
Answers
The resulting equation would be AD = BC. Therefore, to calculate the proportion, you need to multiply the numerator of one ratio by the denominator of the other ratio and equate the products.
What are proportions? Proportions are two ratios that are equivalent or equal to each other. The ratios can be represented as a fraction or a decimal. Proportions are useful in math when dealing with solving problems that involve ratios or comparisons between two values or quantities. How to calculate proportions? To calculate a proportion, you need to compare two ratios. For instance, if you have two ratios A:B and C:D, the proportion will be A:B = C:D. It implies that A is to B as C is to D. Then you can cross-multiply the proportion, which means multiplying the numerator on the left by the denominator on the right, and then multiplying the numerator on the right by the denominator on the left. The proportions that are most useful in analysing the relationship between passenger class and surviving the Titanic are 203/325 and 178/706. The resulting equation would be AD = BC. Therefore, to calculate the proportion, you need to multiply the numerator of one ratio by the denominator of the other ratio and equate the products.
Learn about ratio and proportion here, https://brainly.com/question/2914376
#SPJ11
how is the bell shaped histogram?
Answers
A bell-shaped histogram is a type of graph that displays a normal distribution, which is a probability distribution that is symmetrical and has a characteristic bell shape.
The bell-shaped histogram is created by plotting the data on a horizontal axis and the frequency or probability on a vertical axis. The data points are grouped into intervals called bins, and the number of data points that fall into each bin is plotted as a bar. The bars are typically drawn adjacent to one another and connected with lines to create a continuous curve that represents the normal distribution.
The resulting histogram will have a characteristic bell shape, with a high point at the mean, and decreasing frequency or probability as the values move away from the mean in either direction. The width of the curve is determined by the standard deviation of the data, with wider curves indicating greater variation in the data.
The bell-shaped histogram is commonly used in statistical analysis to represent normally distributed data, such as the heights or weights of a population, test scores, or other measurements that tend to cluster around a central value with a predictable range of variation.
To learn more about bell-shaped histogram please click on below link
https://brainly.com/question/1291520
#SPJ4
let r be a partial order on set s, and t ⊆ s. suppose that a,a′ ∈ t, where a is greatest and a′ is maximal. prove that a = a′
Answers
Let r be a partial order on set S, and let t be a subset of S. If a and a' are both elements of t, where a is the greatest element and a' is a maximal element, then it can be proven that a = a'.
To prove that a = a', we consider the definitions of greatest and maximal elements. The greatest element in a set is an element that is greater than or equal to all other elements in that set. A maximal element, on the other hand, is an element that is not smaller than any other element in the set, but there may exist other elements that are incomparable to it.
Given that a is the greatest element in t and a' is a maximal element in t, we can conclude that a' is not smaller than any other element in t. Since a is the greatest element, it is greater than or equal to all elements in t, including a'. Therefore, a is not smaller than a'.
Now, to prove that a' is not greater than a, suppose by contradiction that a' is greater than a. Since a' is not smaller than any other element in t, this would imply that a is smaller than a'. However, since a is the greatest element in t, it cannot be smaller than any other element, including a'. This contradicts our assumption that a' is greater than a.
Hence, we have shown that a is not smaller than a' and a' is not greater than a, which implies that a = a'. Therefore, if a is the greatest element and a' is a maximal element in t, then a = a'.
To learn more about contradiction click here, brainly.com/question/30373679
#SPJ11
18x^2+4-[6(x^2-2)+5]
Answers
The simplified form of the expression 18x² + 4 - [6(x² -2) + 5] is 12x² + 11.
What is an expression?Mathematical statements are called expressions if they have at least two words that are related by an operator and contain either numbers, variables, or both. Addition, subtraction, multiplication, and division are all possible mathematical operations.
The given expression is
18x² + 4 - [6(x² -2) + 5]
We can rewrite it as
= 18x² + 4 - [6x² - 12 + 5]
= 18x² + 4 - [6x² - 7]
= 18x² + 4 - 6x² + 7
= 12x² + 11
To know more about expressions, visit:
https://brainly.com/question/28170201
#SPJ1
The complete question is:
Simplify the expression: 18x² + 4 - [6(x² -2) + 5]
from a deck of 52 cards, one card is selected. what is the probability that it is a red card or a king
Answers
Answer:
1/2
Step-by-step explanation:
The probability of a random card being red is 1/2 since half the cards are red and half are black
The probability of selecting a red card or a king from a deck of 52 cards is 28/52, which can be simplified to 7/13.
To find the probability of selecting a red card or a king from a deck of 52 cards, follow these steps:
1. Determine the total number of red cards in the deck. There are 26 red cards, as there are 13 cards of each red suit (hearts and diamonds).
2. Determine the total number of kings in the deck. There are 4 kings, one from each suit.
3. Determine the overlap between red cards and kings. There are 2 red kings (king of hearts and king of diamonds).
4. Use the principle of inclusion-exclusion to account for the overlap. This means we'll add the probabilities of the two individual events and subtract the probability of their intersection (overlap).
5. Calculate the probability of each event and their intersection:
- Probability of a red card: 26/52 (number of red cards / total cards)
- Probability of a king: 4/52 (number of kings / total cards)
- Probability of a red king: 2/52 (number of red kings / total cards)
6. Apply the inclusion-exclusion principle:
- Probability of a red card or a king = (Probability of a red card) + (Probability of a king) - (Probability of a red king)
- Probability = (26/52) + (4/52) - (2/52) = 28/52
So, the probability of selecting a red card or a king from a deck of 52 cards is 28/52, which can be simplified to 7/13.
Learn more about "probability": https://brainly.com/question/13604758
#SPJ11
Select all expressions that show "X" increased by 35%.
a
1.35X
b
(35/100)X
c
x + (35/100)
d
( 1+0.35)x
e
(100+35) + x
f
(100 + 35)x
Answers
All the equivalent expressions are,
1.35X and (1+0.35)x.
The correct options are a and d.
What is a percentage?A ratio or value that may be stated as a fraction of 100 is called a percentage. And it is represented by the symbol '%'.
Given:
The value of X increased by 35%.
Here, we will use the percentage formula.
The value is increased by 35%.
That means,
100 + 35 = 135%
135% in decimal form is 1.35.
In expression form as subject to X,
X(1.35)
In expressed form,
= X + 0.35X
= 1.35X
Therefore, equivalent expressions are 1.35X and (1+0.35)x.
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ2
What is 75% of 85$?
Pls help
Answers
Answer:63.75 :)
Step-by-step explanation:
Answer:
$63.75
Step-by-step explanation:
85 x 75/100
85/1 x 3/4
255/4 - > $63.75
- You should already know how to do this yourself as this is very easy and basic question.
Write down the factors of 28 Then,write down the prme factors of 28
Answers
the factors of 28 are : 1, 2, 4, 7, 14, and 28.
the prime factors of 28 are : 2, 2, and 7.
12x+16=14x-2
Please help ASAP
Answers
Answer: the answer is x=9
Step-by-step explanation:
A company pays $150 for a shirt design plus $8 per shirt. An expression can be written to represent the total amount, in dollars, the company pays for n shirts. Which phrases describe the part of the expression that represents the variable cost of n shirts? Select the two correct answers. A the sum of 150 and n B a term with a coefficient of 150 C the term with a coefficient of 8 D the sum of 8 and 150 E the product of 8 and
Answers
By answering the given question, we may state that Option E) The variable variable cost is not included in the formula, but the product of 8 and n does indicate the overall cost of n shirts.
What is a Variable?A variable is anything that may be altered in the context of an experiment or mathematical idea. A single symbol is frequently used to denote a variable. Generic symbols for variables are the letters x, y, and z. Variables are qualities with a wide range of values that may be investigated. These include characteristics like height, age, wealth, place of birth, academic standing, and kind of residence, to mention a few. The two primary groups of variables can be separated using numerical and categorical approaches.
D) The expression with an 8-coefficient
D) The quantity 8 + 150
Option A) As th fixed cost is constant regardless of how many shirts are manufactured, it is represented by the sum of 150 and n.
Option B) The 150-coefficient phrase denotes the fixed cost of the one-time payment for the shirt design.
Option E) The variable cost is not included in the formula, but the product of 8 and n does indicate the overall cost of n shirts.
To know more about variable visit:
https://brainly.com/question/2466865
#SPJ1
Find the solution(s) to: LaTeX: \ln\left(x^2-30\right)=\ln\left(13x\right)ln ( x 2 − 30 ) = ln ( 13 x ) Check for extraneous solutions. Group of answer choices LaTeX: x=\ln15x = ln 15 LaTeX: x=-2,\:x=15x = − 2 , x = 15 LaTeX: x=-2x = − 2 LaTeX: x=15x = 15
Answers
The extraneous solutions of the equation is -2 and 15.
ln stands for logarithm and it is a function that returns the power to which a certain number (base) must be raised to obtain a given value. The logarithm is commonly used to simplify mathematical expressions and can be thought of as an inverse operation to exponentiation.
In this equation, we have two logarithmic expressions on the left and right side. To solve for x, we need to find what number raised to the power of the base (ln), will result in x² - 30 and 13x.
So, if we find the height for one triangle, we can find the height for the other triangle. To do this, we will use the logarithmic property:
ln(aᵇ) = b * ln(a)
Where a and b are any positive real numbers.
Applying this property to both logarithmic expressions, we get:
ln(x² - 30) = ln((x² - 30)^(1/ln)) = 1/ln * ln(x² - 30)
Equating the two, we get:
1/ln * ln(x² - 30) = 1/ln * ln(13) + 1/ln * ln(x)
Dividing both sides by 1/ln, we get:
ln(x² - 30) = ln(13) + ln(x)
Using the logarithmic property, we can simplify further:
x² - 30 = 13 * x
Dividing both sides by x, we get:
x²/x - 30/x = 13
x - 30/x = 13
x² - 30 = 13x
x² - 13x - 30 = 0
This is a quadratic equation and can be solved using the quadratic formula:
x = (-b ± √(b² - 4ac)) / 2a
Where a = 1, b = -13, c = -30
So,
x = (-(-13) ± √((-13)^2 - 4 * 1 * -30)) / 2 * 1
x = (13 ± √(169 + 120)) / 2
x = (13 ± √289) / 2
x = (13 ± 17) / 2
So,
x = (13 + 17) / 2 = 15 or
x = (13 - 17) / 2 = -2
These are the two solutions to the equation. To check for extraneous solutions, we substitute x = 15 and x = -2 back into the equation and see if it is true.
Complete Question:
Find the solution(s) to\(\ln\left(x^2-30\right)=\ln\left(13x\right)\ln ( x^2 - 30 ) = ln( 13 x )\)
Check for extraneous solutions.
To know more about logarithm here
https://brainly.com/question/22626979
#SPJ4
two cards are chosen at random from a deck of 52. what is the probability that both cards are numbers (2 through 10) totaling to 12
Answers
The probability is 0.3845.The probability of anything occurring is known as probability.
How are probabilities calculated?The probability of anything occurring is known as probability. To determine probability, divide the total number of possible outcomes by the number of possible ways an event could occur.The likelihood or chance that a specific event will occur is represented by a probability. Both proportions between 0 and 1 and percentages between 0% and 100% can be used to describe probabilities.To determine probability, divide the total number of possible outcomes by the number of possible ways an event could occur.Explanation:
2/52 * 10/52 = 20/52 = 0.3845.
To learn more about probability refer to:
https://brainly.com/question/24756209
#SPJ4
The lines 2x=ky+2 and (k+1)x=6y-3 have same gradient. Find possible values of k
I need the answers ASAP please!
Answers
Answer:
k = 3 or k = -4
(Anyone can correct me if I'm wrong)
Step-by-step explanation:
\(2x=ky+2\to\ eq1\\(k+1)x=6y-3\to\ eq2\\$Change to this form: $y=mx+c\\ky=2x-2\\y=\frac{2x-2}{k}\\$gradient of eq1: $\frac{2}{k}\\6y=(k+1)x+3\\y=\frac{(k+1)x+3}{6}\\y=\frac{k+1}{6} x+\frac{3}{6}\\y= \frac{k+1}{6} x+\frac{1}{2}\\$gradient of eq1: $\frac{k+1}{6}\\$Since gradient, m, is the same for both lines,$\\\frac{2}{k}=\frac{k+1}{6}\\12=k^{2}+k\\k^{2}+k-12=0\\(k-3)(k+4)=0\\k=3 $ or $ k=-4\)
please use the following scores to answer questions 2a and 2b: x y 1 6 4 1 1 4 1 3 3 1
Answers
The correlation coefficient between the x and y scores is -2.167.
I will use the provided scores to answer questions 2a and 2b.
2a) Calculate the mean of the x scores.
To calculate the mean of the x scores, we add up all the x scores and divide by the total number of scores:
mean = (1 + 4 + 1 + 1 + 3)/5 = 2
Therefore, the mean of the x scores is 2.
2b) Calculate the correlation coefficient between the x and y scores.
To calculate the correlation coefficient between the x and y scores, we first need to calculate the covariance between the x and y scores:
cov(x,y) = (1-2)(6-2) + (4-2)(1-2) + (1-2)(4-2) + (1-2)(3-2) + (3-2)*(1-2) = -10
Next, we need to calculate the standard deviations of the x and y scores:
s_x = sqrt([(1-2)^2 + (4-2)^2 + (1-2)^2 + (1-2)^2 + (3-2)^2]/4) = 1.247
s_y = sqrt([(6-2)^2 + (1-2)^2 + (4-2)^2 + (3-2)^2]/4) = 2.309
Finally, we can calculate the correlation coefficient:
r = cov(x,y)/(s_x * s_y) = -10/(1.247 * 2.309) = -2.167 (rounded to three decimal places)
Therefore, the correlation coefficient between the x and y scores is -2.167.
To know more about refer here:
https://brainly.com/question/31101410
#SPJ11
Here's a little something that will tease your brain. I doubt someone will answer this

Answers
Answer:
500ml orange juice is the most cost effective
If m ∠ E F G = 35 ° and m ∠ G F H = 63 ° , what is m ∠ E F H ?
Answers
Answer:
28°
Step-by-step explanation:
63 -35 = 28
100 meters is how many yards?
Answers
Answer: approx 109 yards (109.36133 yards)
Step-by-step explanation:
1 meter = 1.0936133 yards
100 x 1.0936133 = 109.36133 yards
approx 109 yds
3. When did the law become effective?
Answers
Answer:
which law?
Step-by-step explanation:
A certain plane is described by 2x+3y+4z=16. Find the unit vector normal to the surface in the direction away from the origin.
Answers
A certain plane is described by 2x+3y+4z=16. Find the unit vector normal to the surface in the direction away from the origin.Firstly, we will obtain the coefficients of the x, y and z variables from the equation of the plane:2x + 3y + 4z = 16The coefficients are 2, 3, and 4 respectively.
Now, we will calculate the magnitude of the normal vector, ||N||, using the formula:||N|| = √(a² + b² + c²)where a, b, and c are the coefficients of the x, y, and z variables respectively.||N|| = √(2² + 3² + 4²)= √(4 + 9 + 16)= √29Therefore, the unit normal vector in the direction away from the origin is given by:N = (2/√29) i + (3/√29) j + (4/√29) k. Given the equation of a plane as 2x + 3y + 4z = 16, we have to find the unit vector normal to the surface in the direction away from the origin. Here's how we can do it:To find the unit vector normal to the surface, we first need to find the coefficients of the x, y, and z variables from the equation of the plane. In this case, the coefficients are 2, 3, and 4 respectively.Next, we can use the formula ||N|| = √(a² + b² + c²) to calculate the magnitude of the normal vector, where a, b, and c are the coefficients of the x, y, and z variables respectively. In this case, ||N|| = √(2² + 3² + 4²) = √29.Finally, we can find the unit normal vector in the direction away from the origin by dividing each coefficient by the magnitude of the normal vector, ||N||. Thus, the unit normal vector is:N = (2/√29) i + (3/√29) j + (4/√29) k
Therefore, the unit vector normal to the surface in the direction away from the origin is (2/√29) i + (3/√29) j + (4/√29) k.
To learn more about unit vector normal visit:
brainly.com/question/30895179
#SPJ11
find a formula for rn for the function f(x) = (3x)2 on [−1, 5] in terms of n.
Answers
The formula for for Rn is given as Rn = Σ 18/n (1 - 12i/n + 36i²/n²).
We are given the function f(x) = 3x² on the interval [-1, 5] . This gives
Δx =6/n and xi= -1 + 6i/n.
Therefore,
Rn = Σ f(xi) Δx
= Σ 3 (-1 + 6i/n)² 6/n
= Σ 18/n (1 - 12i/n + 36i²/n²)
The limit of a function in mathematics is a key idea in calculus and analysis regarding the behavior of that function close to a specific input.
Informally, a function f gives each input x an output f(x). If f(x) approaches L as x approaches input p, we say that the function has a limit L at that location. More specifically, any input that is sufficiently close to p when f is applied forces the output value arbitrarily close to L.
The concept of limit is specifically used in the various definitions of continuity. Roughly speaking, a function is continuous if all of its limits agree with the values of the function. The term "limit" is also used in the definition of the mathematical term "derivative," which in one-variable calculus refers to the maximum value of the slope of secant lines on a function's graph.
To more about Limit :
https://brainly.com/question/282767
#SPJ4
what are prime factors
Answers
Answer:
Prime factors are numbers that can be combined to create a specific number.
Example:
Prime factors of 64 :
1*64=64
2*32=64
4*16=64
8*8=64
I really hope I'm correct I could be wrong but this is what I remember. Hope it helps!
Which choice is equivalent to the expression below? 27.19 O A. 27+1/10 + 9/10 O B. 27. 219/10 c. 27. 21/10.29/100 O D. 2? + 21/10 + 29/100
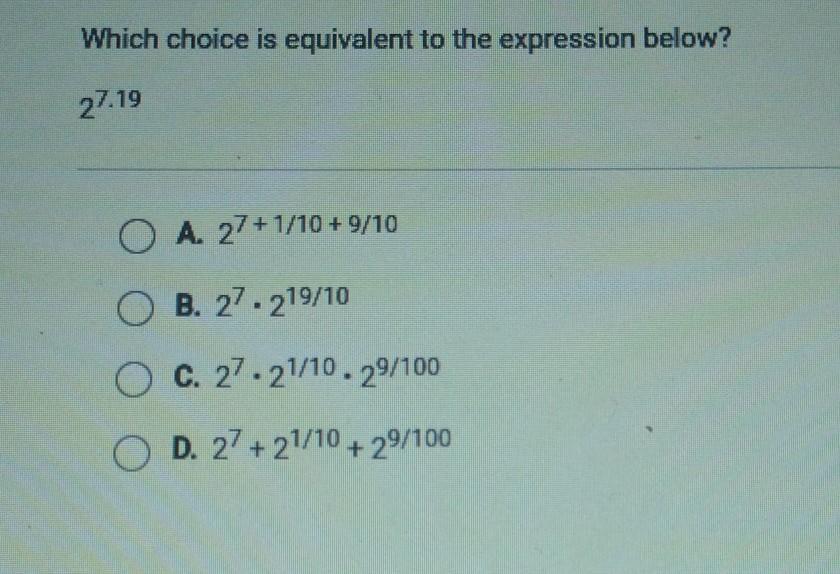
Answers
The choice that is equivalent to the expression \(2^{(7.19)}\) is option C: \((2^7 )(2^{(1/10)}) (2^{(9/100)})\).
To know why option C is the right choice, break down the expression \(2^{(7.19)}\). The exponent 7.19 can be written as the total sum of 7, 0.1, and 0.09:
7.19 = 7 + 0.1 + 0.09.
According to the laws of exponents, we can rewrite \(2^{(7.19)}\) as:
\(2^{(7 + 0.1 + 0.09)}\).
Now, using the rule that says when you raise a power to another power, you multiply the exponents, we can split the expression into three parts:
\((2^7) (2^{0.1}) (2^{0.09})\).
This is exactly the form presented in option C, where \(2^7\) represents the first part, \(2^{(1/10)}\) represents the second part, and \(2^{(9/100)}\) represents the third part.
For more questions on laws of exponents
https://brainly.com/question/11761858
#SPJ8
