Do these side lengths make a right triangle? 6, 8, 10
Answers
Answer:
Yes
Step-by-step explanation:
\(6^{2}\) + \(8^{2}\) = \(10^{2}\)
36 + 64 = 100
The Pythagorean theorem is true.
Related Questions
What is x3 = 8/27
Help me please
Answers
Answer: x=8/81
Step-by-step explanation
3x divide by 3
8/27 divide by 3
it becomes x=8/27 divide by 3 and 3 becomes 1/3
8/27 x 1/3=8/81
x=8/81
A newspaper publisher decides to sell ads to cover 5/8 of the center page. If each ad covers 1/16 of a page, how many ads will be on the page?
Answers
Answer:
10 ads
Step-by-step explanation:
10/16=5/8 and 1 covers 1/16th of a page he is going to put 10 on the page
Jual Tecipe, the ratio of carrots to cucumbers must remain constant. The table below shows some possible combinations of carrots and cucumbers. Salad Ingredients Carrots Cucumbers 3 9 4 12 6 18 7 21 If only whole vegetables can be used, what is the fewest number of vegetables that can be used to make this salad? 1 3 0 4 12 Save and Exit Next Submit Mark this and return

Answers
The two vegitables to be used are cucumbers and carrots. We are told that the ratio of the combination must be constant. From the question, we can see that the constant ratio of carrot to cucumber is 1:3. This is determined by simplifying each combination to its lowest term. Therefore, if onlthe least
Can someone help mean I know this is easy but it’s not to me lol

Answers
Answer:
I. Not a function
II. Not a function
III. Yes, function
IIII. Yep!
(I messed up the numbering in the explanations, sorry 3 is 4 and 4 is 3)
Step-by-step explanation:
Hi!
For a function, every x value must have exactly 1 y value.
f(2) can't equal both 0 and 10. It can only equal 0 or 10. So, because of this, we have a test called the vertical line test. Basically, you drag a line through a graph, and if there is any x value that goes to two (or more) different y-values, then that graph is not the graph of the function.
Let me try to give a practical explanation.
I.
In this graph, everything looks fine until we reach x=6. (I'm assuming the graph goes by ones). Do you see the problem? Yep! x has two different y values.
y= 4 and y= 6.
So, this isn't a function. Why? Because there are two y values for each x value (aka, this doesn't pass the V.L.T)
II.
(1,2), (2,5) , (3,8) , (2,-5) (1,-2)
We have two groups of problem points.
(2,5) and (2,-5) and (1,2) and (1,-2)
Here, each x value goes to a different y value. Therefore, this isn't a function
III. y=x^2
This is your typical parabola. See the graph that I attached.
Notice that -2 and 2 both go to 4. Two different x-values going to the same y-value is fine, but one x can't go to to different y values.
IIII.
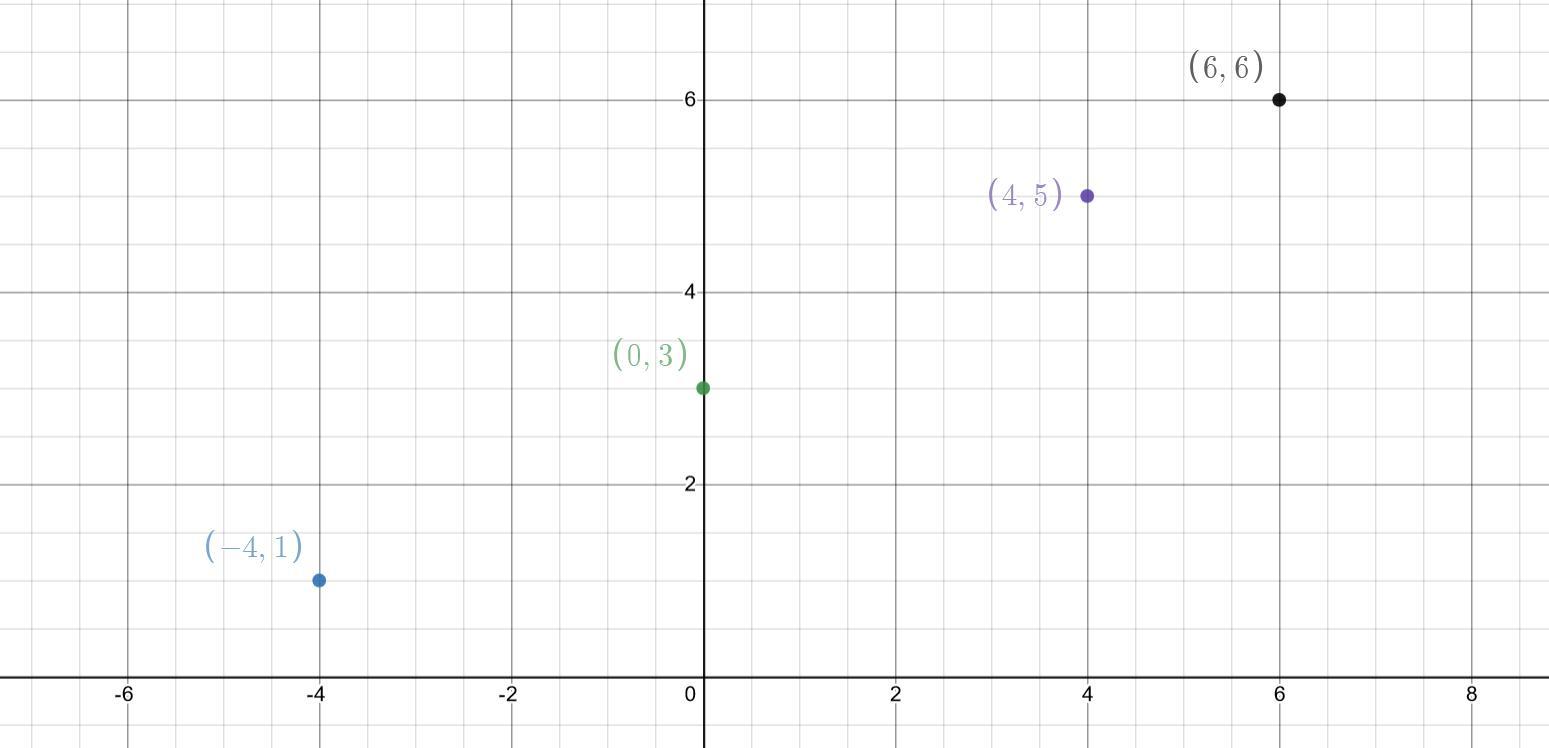
(-4,1) , (0,3) , (4,5) , (6,6)
Check 1: Does any x-value go to multiple y values? Nope! So, this is a function.


whos interested in anime, if u are i got suggestions. oh and can i get an answer for this haha
Evaluate this power with a base that is a negative fraction.
(−1/4) ²
What is the value of the power?
- 2/4
- 1/16
1/16
1/8
Answers
Answer:
1/16
When you calculate they both get the answer 0.0625
Suppose that the function f is given by f(z, 3) = 4 – 8 – +1. Find the critical points of f. For each critical point of f. determine whether it is a local minimum, local maximum, or a saddle point.
Answers
The critical point of f at z = 1 is a local minimum.
To find the critical points of the function f(z, 3) = 4z^2 - 8z + 1, we need to find the values of z where the first partial derivatives with respect to z are equal to zero. Let's solve it step by step.
Take the partial derivative of f with respect to z:
∂f/∂z = 8z - 8
Set the derivative equal to zero and solve for z:
8z - 8 = 0
8z = 8
z = 1
The critical point of f occurs when z = 1.
To determine whether the critical point is a local minimum, local maximum, or a saddle point, we can use the second partial derivative test. We need to calculate the second partial derivative ∂²f/∂z² and evaluate it at the critical point (z = 1).
Taking the second partial derivative of f with respect to z:
∂²f/∂z² = 8
Evaluate the second derivative at the critical point:
∂²f/∂z² at z = 1 is 8.
Analyzing the second derivative:
Since the second derivative ∂²f/∂z² = 8 is positive, the critical point (z = 1) corresponds to a local minimum.
Therefore, the critical point of f at z = 1 is a local minimum.
learn more about local minimum here
https://brainly.com/question/29184828
#SPJ11
Let A = {-2, -1, 0, 1, 2, 3, 4, 5, 6, 7} and define a relation R on A as follows: For all x, y EA, x Ry 31(x - y). It is a fact that R is an equivalence relation on A. Use set-roster notation to write the equivalence classes of R.
[0] = [1] = [2] = [3] =
Answers
The equivalence classes of the relation R on set A = {-2, -1, 0, 1, 2, 3, 4, 5, 6, 7} can be represented as [0] = {0}, [1] = {1, 2}, [2] = {2, 3, 4}, and [3] = {3, 4, 5, 6, 7}.
In this problem, the relation R on set A is defined as x Ry if and only if 3(x - y) = 1. To determine the equivalence classes, we need to find all elements in A that are related to each other under R.
Starting with [0], the equivalence class of 0, we find that 3(0 - 0) = 0, which satisfies the condition. Therefore, [0] = {0}.
Moving on to [1], the equivalence class of 1, we need to find all elements in A that satisfy 3(x - 1) = 1. Solving this equation, we find x = 2. Therefore, [1] = {1, 2}.
Similarly, for [2], the equivalence class of 2, we solve 3(x - 2) = 1, which gives x = 3. Hence, [2] = {2, 3}.
Finally, for [3], the equivalence class of 3, we solve 3(x - 3) = 1, which gives x = 4. Thus, [3] = {3, 4}.
Since there are no more elements in A to consider, the equivalence classes [0], [1], [2], and [3] represent all the distinct equivalence classes of the relation R on set A.
Learn more about equivalence relations.
brainly.com/question/30901467
#SPJ11
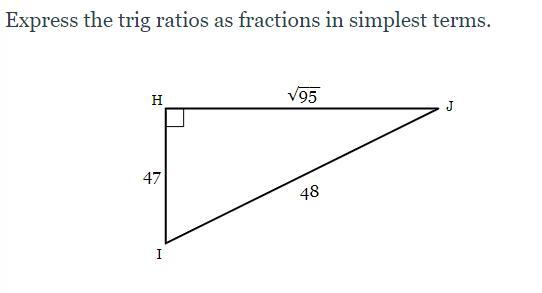
Express the trig ratios as fractions in simplest terms.
Answers
The trigonometric ratios for each angle are found for the given right triangle as shown below.
What is meant by trigonometric ratios?
Trigonometric ratios are the values of all trigonometric functions based on the right-angled triangle's side ratio. The trigonometric ratios of a given acute angle are the ratios of the sides of a right-angled triangle with respect to that angle. Sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant(sec) are the six trigonometric ratios . A branch of mathematics called trigonometry in geometry deals with the sides and angles of a right-angled triangle.
In this question, we are given a right triangle.
From the triangle, we can write the following.
Hypoyenuse = longest side = 48
Height = 47
Base = √95 = 9.75
With respect to angle ∠J, we can find the trigonometric ratios.
Let ∠J = Ф
sin Ф = Opposite side/ hypotenuse = 47/48 = 0.98
cos Ф = adjacent side/ hypotenuseuse = √95/48 = 0.20
tan Ф = opposite side/adjacent side = 47/√95 = 4.82
cosec Ф = 1/sinФ = 1/ 0.98 = 1.02
sec Ф = 1/cos Ф = 1/0.20 = 5
cot Ф = 1/tan Ф = 1/4.82 = 0.21
With respect to the angle ∠I, we can find the trigonometric ratios.
Let ∠I = θ
sin θ = Opposite side/ hypotenuse = √95/48 = 0.20
cos θ = adjacent side/ hypotenuseuse = 47/48 = 0.98
tan θ = opposite side/adjacent side = √95/47 = 0.21
cosec θ= 1/sinФ = 1/ 0.20 =5
sec θ = 1/cos Ф = 1/0.98 = 1.02
cot θ = 1/tan Ф = 1/0.21= 4.8
Therefore trigonometric ratios for each angle are found for the given right triangle.
To learn more about trigonometric ratios, follow the link.
https://brainly.com/question/24349828
#SPJ1
Find the exterior angle for each

Answers
Step-by-step explanation:
In all cases just divide 360° by the number of sides
Thus,for a. 360°/12=30°
Answer:
1. the total triangles of 12 sides are 10 triangles but the exterior angles of a 12 sided polygon is 30° because dodecagon is equal to 150°
2. the total triangles of 18 sides are 16 triangles but the exterior angles of a 18 sided polygon is 20° because octakaidecagon is equal to 360°/18=20°
3. the total triangles of 8 sides are 6 triangles but the exterior angles of a 6 sided polygon is 120° because hexagon is equal to 720°/6=120°
4. the total triangles of 3 sides are 1 triangle but the exterior angles of a 6 sided polygon is 60° because hexagon is equal to 180°/3=60°
Evaluate the following.
5!
A)15
B)120
C)720
Answers
Answer:
120
Step-by-step explanation:
5!
The factorial means multiply that number and all the numbers below it to 1
5! = 5*4*3*2*1
120
Answer:
B
Step-by-step explanation:
n! = n(n - 1)(n - 2) ..... × 3 × 2 × 1
Then
5! = 5 × 4 × 3 × 2 × 1 = 120
sarah has 1/2 of a pound of chocolate. she breaks off 1/16 pound to eat each night after dinner. How many nights will sarah have chocolate?
Answers
Answer:
8 nights
Step-by-step explanation:
integrated math 2 chapter!help please i’m so lost :(

Answers
To solve this problem, you have to know that the measure of all the angles of a triangle is equal to 180 degrees.
Let's add each angle together and set them equal to 180 degrees.
180 degrees = 3x + 2x + 1 + x + 5
Combine like terms
180 degrees = 6x + 6
Subtract 6 from both sides
174 degrees = 6x
Divide both sides by 6
29 = x
We know that angle A = 3x = 3(29) = 87 degrees.
Another of Bhaskara's problems results in a quadratic equation Parthava was enraged and seized a certain number of arrows to slay Karna. He expended one-half of them in defending himself. Four times the square root of the number of arrows were discharged against the horses. With six more, he transfixed Shalya, the charioteer. With three more, he rent the parasol, the standard, and the bow; and with the last one he pierced the head of Karna. How many arrows did Parthava have?
Answers
Answer:
Parthava had 100 arrows.
Step-by-step explanation:
Let's define N as the number of arrows that Parthava originally has.
He uses one-half of them in defending himself, so he used N/2 arrows
Now he uses four times the square root of the number of arrows, so now he uses:
4*√N
Then he uses 6
Then he uses 3
Then he uses the last one.
If we add all these numbers of arrows that he used, we should get the initial number of arrows that he used, then:
N/2 + 4*√N + 6 + 3 + 1 = N
Now we have an equation that we can try to solve.
First, let's move all the terms to the same side:
N/2 + 4*√N + 6 + 3 + 1 - N = 0
now we can simpify it:
(N/2 - N) + 4*√N + (6 + 3 + 1) = 0
-(1/2)*N + 4*√N + 10 = 0
Now we can define a new variable x = √N
Then we have: x^2 = N
now we can replace these new variables in our equation to get:
-(1/2)*x^2 + 4*x + 10 = 0
Now we just have a quadratic equation.
Remember that for a quadratic equation of the form:
0 = a*x^2 + b*x + c
The solutions were given by:
\(x = \frac{-b \pm \sqrt{b^2 - 4*a*c} }{2a}\)
Then in our case, the solutions will be:
\(x = \frac{-4 \pm \sqrt{4^2 - 4*(-1/2)*10} }{2*(-1/2)} = \frac{-4 \pm 6 }{-1} = 4 \pm 6\)
So there are two solutions:
x = 4 + 6 = 10
x = 4 - 6 = -2
And remember that x = √N
Then x should be positive, then we take x = 10 as our solution here.
then we can use the equation:
x = 10 = √N
then
10^2 = √N^2 = N
10^2 = 100 = N
Parthava had 100 arrows.
Find the perimeter area and/or volume of the given figure
Answers
According to the information the volume of this figure would be 16cm³ and the surface area of this figure would be 24cm²
How to calculate the surface area and volume of this figure?To calculate the surface area and volume of this figure we must perform the following procedure:
Volume:
Multiply height, width and length
2cm * 2cm *2cm = 16cm³
Surface area:
Multiply height by width and multiply the result by the number of faces the figure has.
2cm * 2cm = 4cm²
4cm² * 6 = 24cm²
According to the above, the volume of this figure is 16cm³ and the surface area is 24cm².
Learn more about surface area at: https://brainly.com/question/29101132
#SPJ1

PART 1: Sam brings x burgers to the BBQ. his friends Mike brings 5 more than 2 times as many burgers as Sam did. together they brought 50 burgers. please write an equation to represent this situationPART 2: solve the equation you created in part 1 for xPART 3: how many burgers did Mike to the BBQ
Answers
The number of burger sam bought = x
Let the number of burgers for mike be = y
the equation for the total number of burgers will be
\(x+y=50\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots(\text{eqn 1)}\)Mike brought 5 more than 2 times as many burgers as sam will be represented as
\(y=2x+5\ldots\ldots\ldots\ldots\ldots\ldots\ldots..(Eqn\text{ 2)}\)By substituting Eqn 2 in Eqn 1 we will have
\(\begin{gathered} x+y=50 \\ x+2x+5=50 \\ 3x+5=50 \\ 3x=50-5 \\ 3x=45 \\ \frac{3x}{3}=\frac{45}{3} \\ x=15 \end{gathered}\)Therefore,
The value of x= 15
To calculate the number of burgers mike brought to the BBQ =y,
We will substitute the value of x in (Eqn 1) above
\(undefined\)
I.Write the algebraic expressions for the following statements:
1. The sum of a and b subtracted from 5.
2. A number added to half of itself.
3. 2 less than 2times of x.
4. Product of numbers m and n added to 7.
5. One-third of the sum p and q subtracted from the product of p and q.
6. A number a multiplied by itself.
Answers
Answer:
1. 5 - (a+b)
2. n + 0.5n = 1.5 n
3. 2x - 2
4. 7 + mn
5. pq - (p+q)/3
6. a*a = a^2
Step-by-step explanation:
what is an equation of the line passing through the points (-1,7) (-7,1)
Answers
Step-by-step explanation:
For us to write the equation for this line, we need to (1) find the slope of the line, and (2) use one of the points to write an equation:
The question gives us two points, (-1, 7) (-7, 1), from which we can find the slope and later the equation of the line.
Finding the Slope
The slope of the line (m) = (y₂ - y₁) ÷ (x₂ - x₁)
= (7 - 1) ÷ (-1 - (-7))
= 6 ÷ 6
= 1
Finding the Equation
We can now use the point-slope form (y - y₁) = m(x - x₁)) to write the equation for this line; where (x₁ , y₁) = (-1, 7):
⇒ y - 7 = (x + 1)
we could also transform this into the slope-intercept form ( y = mx + c)
since y - 7 = (x + 1)
y = x + 1 + 7
⇒ y = x + 8
To test my answer, I have included a Desmos Graph that I graphed using the information provided in the question and my answer.
I need help for this problem what do I have to do ?

Answers
=>10x+2=128°
=>10x=128-2
=>10x=126
=>x=126/10=63/5
=>x=12.6°
Answer:
X = 5
Step-by-step explanation:
1. first, remember that it is a straight Angle.
straight angles always add up to 180.
Equation should be -
10x+2 +128= 180
so you are solving for X
Add 128 and 2= 130
subtract 130 on both sides
2. You remain With 10x=50
Then You divide 50/10
you get 5
3. If You would like, Try checking This answer.
10x+2
when x= 5
10x5 +2 +128 = 180
5 =x
I hope helps!
have a wonderful Day!
an experiment consists of tossing 4 unbiased coins simultaneously. the number of simple events in this experiment is question 20answer a. 10 b. 8 c. 16 d. 25
Answers
The number of simple events in this experiment is 16.
The correct answer to the given question is option c.
The probability of an event can be calculated by dividing the number of favorable outcomes by the number of possible outcomes. A simple event is one in which only one of the outcomes can occur. For example, if a coin is tossed, a simple event would be the outcome of the coin being heads or tails.
The total number of possible outcomes in the experiment of tossing 4 unbiased coins simultaneously is 2⁴, since there are two possible outcomes for each coin. Thus, the total number of possible outcomes is 16.
Each coin has two possible outcomes: heads or tails. If all four coins are flipped, there are two possible outcomes for the first coin, two possible outcomes for the second coin, two possible outcomes for the third coin, and two possible outcomes for the fourth coin. Therefore, the total number of possible outcomes is 2 × 2 × 2 × 2 = 16.
Therefore, the number of simple events in this experiment is 16, which is option (c).
For more such questions on simple events, click on:
https://brainly.com/question/10346457
#SPJ8
Please hurry!!! ill give branliest! In a certain candy store, 3 pounds of candy and 2 pounds of mints cost $10.80, and 1 pound of candy and 3 pounds of mints cost $5.35. What is the cost per pound of the mints?
a.mints are 75¢ per lb
b.mints are 85¢ per lb
c.mints are 65¢ per lb
Answers
Answer:
mints are 75 cents per lb
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
Let's make two equations from the question:
\(3x+2y=10.8\\x+3y=5.35\)
If we graph these equations we see that the intersection of these equations are (3.1, 0.75), so the correct answer is A, it costs 75 cents.

fausting aged 10 and Ernesting aged 12 Share GHd 55.00 in the ratio of their ages. How much does Fausting receive?
Answers
Fausting receives GHd 25.00 of the GHd 55.00.
The ratio of Fausting's age to Ernesting's age is 10:12 can be simplified to 5:6 by dividing both sides by 2.
The GHd 55.00 Fausting receives need to determine the fraction of the total amount that corresponds to his share of the ratio:
Fausting's share = 5 / (5 + 6)
= 5/11
Ernesting's share = 6 / (5 + 6)
= 6/11
Fausting's share in Ghanaian cedi (GHd) can multiply the total amount by the fraction representing his share:
Fausting's share = GHd 55.00 x 5/11
= GHd 25.00 (rounded to the nearest GHd)
Fausting receives GHd 25.00 of the GHd 55.00.
By dividing both sides by 2, the ratio of Fausting's and Ernesting's ages is 10:12 may be reduced to 5:6.
To calculate his part of the ratio for the GHd 55.00 Fausting gets, divide the total by the ratio:
Share of Fausting is 5 / (5 + 6) = 5/11.
Ernesting's portion equals 6 / (5 + 6) to 6/11.
The fraction that represents Fausting's share may be used to multiply the total sum by in Ghanaian cedi (GHd):
Fausting's share equals (rounded to the closest GHd): GHd 55.00 x 5/11 = GHd 25.00.
Of the GHD 55.00, Fausting receives GHD 25.00.
For similatr questions on GHd
https://brainly.com/question/26139520
#SPJ11
Qd=95−4P
Qs=5+P
a. What is Qd if P=5 ? b. What is P if Qs=20 ? β=9 c. If Qd=Qs, solve for P.
Answers
P = 90 is the solution for the given equation.
Given: Qd=95−4
PQs=5+P
To find Qd if P=5:
Put P = 5 in the equation
Qd=95−4P
Qd = 95 - 4 x 5
Qd = 75
So, Qd = 75.
To find P if Qs = 20:
Put Qs = 20 in the equation
Qs = 5 + PP
= Qs - 5P
= 20 - 5P
= 15
So, P = 15.
To solve Qd=Qs, substitute Qd and Qs with their respective values.
Qd = Qs
95 - 4P = 5 + P
Subtract P from both sides.
95 - 4P - P = 5
Add 4P to both sides.
95 - P = 5
Subtract 95 from both sides.
- P = - 90
Divide both sides by - 1.
P = 90
Thus, P = 90 is the solution for the given equation.
To know more about substitute visit
https://brainly.com/question/29383142
#SPJ11
giving away 100 points and mark brainiest
Justine graphs the function f(x) = (x – 7)2 – 1. On the same grid, she graphs the function g(x) = (x + 6)2 – 3. Which transformation will map f(x) on to g(x)? left 13 units, down 2 units right 13 units, down 2 units left 13 units, up 2 units right 13 units, up 2 units
Answers
Answer:
The answer is in the picture and 100%correct.
it helped me thrice so I hope it to help you too!

write the equation of the parabola that has its x-intercepts at (-1.6, 0) and (-3.2, 0) and its y-intercept at (0, 25.6)
Answers
The equation of the parabola that has its x-intercepts at (-1.6, 0) and (-3.2, 0) and its y-intercept at (0, 25.6) is 5x² + 8x - 25.6
How to write the equation of the parabola with the x intercepts at (-1.6, 0) and (-3.2, 0)The x intercept refers to the value of x when y = 0 this otherwise known as the roots of the polynomial equation.
The intercept form of parabolic equation is
y = a(x - p)(x - q)
where
p and q are roots
a = constant
writing the equation at (-1.6, 0), (-3.2, 0)
y = a( x + 1.6 ) ( x + 3.2 )
passing through point (0, 25.6)
25.6 = a( 0 + 1.6 ) ( 0 + 3.2 )
25.6 = 5.12a
a = 5
substituting into the equating gives
y = a(x - p)(x - q)
y = 5( x + 1.6 ) ( x + 3.2 )
expanding the equation gives
= 5(x² + 3.2x - 1.6x - 5.12)
= 5(x² + 1.6x - 5.12)
= 5x² + 8x - 25.6
Learn more about polynomial functions here:
https://brainly.com/question/29244637
#SPJ1
To improve reading skills, elementary school children read silently at the end of the school day for 3/4 hour on Mondays and for 1/2 hour on Fridays.
S M T W T F S
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
1.For how many total hours did the children read silently in class on Mondays in the month of January? (Enter your answer as a simplified mixed number.)
2. For how many total hours did the children read silently in class on Fridays in the month of January?
3.For the month of January, for how many total hours did the children read silently in class? (Enter your answer as a simplified mixed number.)
Answers
By answering the presented question, we may conclude that As a result, equation the youngsters read silently in class for 6 1/4 hours in January.
What is equation?An equation in mathematics is a statement that states the equality of two expressions. An equation is made up of two sides that are separated by an algebraic equation (=). For example, the argument "2x + 3 = 9" asserts that the phrase "2x Plus 3" equals the number "9." The purpose of equation solving is to determine the value or values of the variable(s) that will allow the equation to be true. Equations can be simple or complicated, regular or nonlinear, and include one or more elements. The variable x is raised to the second power in the equation "x2 + 2x - 3 = 0." Lines are utilised in many different areas of mathematics, such as algebra, calculus, and geometry.
To answer these questions, we must first know the number of Mondays and Fridays in January:
The letters S M T W T F S
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31
In January, there are five Mondays and five Fridays.
We sum the amount of time the children read silently in class on Mondays and Fridays to get the total amount of time they read silently in class in January:
3 3/4 + 2 1/2 = 6 1/4 hours.
As a result, the youngsters read silently in class for 6 1/4 hours in January.
To know more about equation visit:
brainly.com/question/28982453
#SPJ1
32:51
On a coordinate plane, trapezoids A B D C and M N P Q are shown. The length of A B is 4 units and the length of B D is 2 units. The length of M N is 10 units and the length of N P is 6 units.
Is trapezoid ABDC the result of a dilation of trapezoid MNPQ by a scale factor of Two-fifths? Why or why not?
Yes, because AB and CD are each Two-fifths the lengths MN and QP.
Yes, because sides AB and CD are parallel to sides MN and QP.
No, because AB is Two-fifths the length MN but CD is One-third the length QP.
No, because sides AB and CD have different slopes from sides MN and QP.
Answers
9514 1404 393
Answer:
C. No, because AB is Two-fifths the length MN but CD is One-third the length QP.
Step-by-step explanation:
Dilation multiplies each coordinate or length by the scale factor. Here, different corresponding lengths are multiplied by different values, so no dilation is involved.
__
Additional comment
Dilation shouldn't change any slopes, so if slopes of corresponding segments are different, that is another indication dilation is not involved. (No figure is supplied here, so we cannot judge slopes.)
Answer:
c
Step-by-step explanation:
In ARST, the measure of ZT=90°, the measure of ZS=21°, and ST = 7.7 feet. Find the length of TR to the nearest tenth of a foot. S 21° 7.7 T х E
Answers
In ΔRST, the measure of ∠T=90°, the measure of ∠R=29°, and ST = 6.7 feet. Find the length of TR to the nearest tenth of a foot.
We will draw the rectangle triangle:
We can use the trigonometry property where the sine of an angle (∠R) is equal to the ratio between the opposite side (ST) and the hypotenuse (RS).
Also, the cosine of ∠R is equal to the ratio between the adyacent side (RT) and the hypotenuse (RS).
We can express this as:
\(\begin{gathered} \frac{\sin R}{\cos R}=\frac{\frac{ST}{RS}}{\frac{RT}{RS}}=\frac{ST}{RT}=\tan R \\ \tan (29)=\frac{ST}{RT}=\frac{6.7}{RT} \\ RT=\frac{6.7}{\tan (29)}=\frac{6.7}{0.554}\approx12 \end{gathered}\)The length of TR is 12 feet.

Solve: -7x+2y=-3 2x+4y=42
Answers
i think its three, nine
40 + 3 = 15
HELPpppp
Answers
Step-by-step explanation:
uhm how do i help?
Answer:
umm the answer is actually 43...
Two angle measures in a triangle are 67° and 26°. What is the measure of the third angle?
93°
87°
267°
90°
Answers
Answer:
\( \boxed{Measure \: of \: third \: angle = 87\degree} \)
Step-by-step explanation:
The sum of angles of a triangle equals the straight angle (180°, π radians, two right angles, or a half-turn).
Let measure of the third angle be 'x'
\( = > 67 \degree + 26\degree + x\degree = 180\degree \\ \\ = > 93\degree + x\degree = 180\degree \\ \\ = > x\degree = 180\degree - 93\degree \\ \\ = > x\degree = 87\degree\)