do the data profvide evidnce that there is an association between age-group and whterher or not a person consumes five or more servings of fruits and vegetables per day for adults in hte united states?
Answers
The data provide convincing statistical evidence that there is an association between age group and consumption of fruits and vegetables for adults in the United States.
To determine if the data provide convincing statistical evidence that there is an association between age group and consumption of fruits and vegetables, we can perform a chi-squared test of independence. This test assesses whether there is a statistically significant association between two categorical variables.
The null hypothesis for this test is that there is no association between age group and consumption of fruits and vegetables, and the alternative hypothesis is that there is an association between the two variables.
Using the given data, we can calculate the expected frequencies for each cell under the assumption that there is no association between age group and consumption of fruits and vegetables. We can then use these expected frequencies to calculate the chi-squared test statistic and determine the p-value.
Performing the chi-squared test of independence with the given data yields a test statistic of 300.96 and a p-value of less than 0.0001. This indicates that there is a statistically significant association between age group and consumption of fruits and vegetables.
Learn more about the chi-squared test;
https://brainly.com/question/4543358
#SPJ4
The image of the complete question is given in the attachment.

Related Questions
5. 10 pens are purchased at the rate of Rs 12.30 each. What is the sale price of each, if there is a total gain of Rs 24?
Answers
The sale price of each pen if 10 pens are purchased at the rate of Rs 12.30 each and there is a total gain of Rs 24 is Rs 14.70
What is the sale price of each pen?Total number of pens = 10
Cost of each pen = Rs 12.30
Total gain = Rs 24
Gain on each pen = Total gain / Total number of pens
= Rs 24 / 10
= Rs 2.4
The sale price of each pen = Cost of each pen + Gain on each pen
= Rs 12.30 + Rs 2.4
= Rs 14.70
Hence, each pen is sold at Rs 14.70
Read more on sale price:
https://brainly.com/question/7459025
#SPJ1
All pieces of pizza must be square with none left over. What is the side length of the largest square pieces into which Juanita and Samuel can cut the pizza?
Answers
Answer:
6 in
Step-by-step explanation:
The question is incomplete. Here is the complete question.
Juanita and samuel are planning a pizza party. they order a rectangle sheet pizza that measures 21 inches by 36 inches.? they tell the pizza maker not to cut it because they want to cut it themselves. All pieces of pizza must be square with none left over. what is the side length of the largest square pieces into which juanita and samuel can cut the pizza?
First we need to calculate the area of the rectangular pizza.
Area of a rectangle = Length × Breadth
Area of the rectangular pizza= 21×36
Area of the rectangular pizza = 756in²
Next is to equate the area of the rectangle to the area of a square.
Area of a square = L²
Therefore L² = 756
L = √756
L = √36×21
L = √36×√21
L = 6√21
This means that the length if the largest square they can cut is 6in (ignoring the irrational part of the length gotten)
22 - {[(87 - 32) divided by 5] × 2}
Answers
22 − ( ( ( 87 − 32 ) ÷ 5 ) × 2 )
Simplify each term.
22 − 22
Subtract 22 from 22 .
= 0
You may need to use the appropriate appendix table or technology to answer this question The life expectancy of a particular brand of tire is normally distributed with a mean of 50,000 miles and a standard deviation of 5,000 miles. What percentage of tires will have a life of 45,000 to 55,000 miles 15.87% 31.73% 68,27% 84.13%
Answers
The percentage of tires that will have a life of 45,000 to 55,000 miles is 68.27%. So the correct option is 68.27%.
To find the percentage of tires that will have a life of 45,000 to 55,000 miles, we can use the concept of the normal distribution.
First, we calculate the z-scores for both values using the formula:
z = (x - mean) / standard deviation
For 45,000 miles:
z1 = (45,000 - 50,000) / 5,000 = -1
For 55,000 miles:
z2 = (55,000 - 50,000) / 5,000 = 1
Next, we look up the corresponding values in the standard normal distribution table. The table will provide the proportion of data within a certain range of z-scores.
The percentage of tires with a life between 45,000 and 55,000 miles is the difference between the cumulative probabilities for z2 and z1.
Looking at the standard normal distribution table, the cumulative probability for z = -1 is 0.1587, and the cumulative probability for z = 1 is 0.8413.
Therefore, the percentage of tires that will have a life of 45,000 to 55,000 miles is:
0.8413 - 0.1587 = 0.6826
Converting this to a percentage, we get:
0.6826 * 100 = 68.26%
So the correct answer is 68.27%.
Know more about the normal distribution.
https://brainly.com/question/23418254
#SPJ11
Find (a) the compound amount and (b) the compound interest rate for the given investment and annu $4000 for 5 years at 7% compounded annually (a) The compound amount in the account after 5 years is $ (b) The compound interest earned is $
Answers
The future value (A) is approximately 5610.2 for the given investment and annu $4000 for 5 years at 7% compounded annually
To find the compound amount and compound interest rate for the given investment, we can use the formula for compound interest:
(a) The compound amount in the account after 5 years can be calculated using the formula:
A = P(1 + r/n)^(nt)
Where A is the compound amount, P is the principal (initial investment), r is the interest rate, n is the number of times the interest is compounded per year, and t is the number of years.
Given that the principal (P) is $4000, the interest rate ® is 7%, and the interest is compounded annually (n = 1), and the investment is for 5 years (t = 5), we can plug these values into the formula:
A = 4000(1 + 0.07/1)^(1*5)
A = 4000(1 + 0.07/1)^(1*5)
= 4000(1 + 0.07)^(5)
= 4000(1.07)^(5)
≈ 4000(1.402551)
≈ 5610.20
Therefore, the future value (A) is approximately 5610.2
Calculating this expression will give us the compound amount after 5 years.
(b) The compound interest earned can be calculated by subtracting the principal from the compound amount:
Compound interest = Compound amount – Principa
This will give us the total interest earned over the 5-year period.
By evaluating the expressions in (a) and (b), we can determine the compound amount and the compound interest earned for the given investment.
Learn more about compound interest rate here:
https://brainly.com/question/30501640
#SPJ11
Z varies jointly with x and y. If x = 7, y = 3, and z = −14, write the variation equation and find y when z = −8 and x = 3
Answers
The equation is z = (-2/3)*xy with of x , y and z are jointly varied.
What is Joint Variation ?Joint variation describes a situation in which, while the other variables are held constant, the value of one variable relies on the values of two or more additional variables.
Joint variation is used to describe when more than two variables are directly correlated or when one variable changes as a result of the change product of more than two variables. X can be symbolically expressed as X YZ if it is in joint variation with Y and Z. If Y is also constant, then X and Z directly depend on one another.
Joint variation is a type of variation where a quantity changes when two or more other numbers are multiplied together. For instance, when a rectangle's length or breadth changes, so does its area. Where A is the area, l is the length, and w is the width, we say that A = lw.
Joint Variation of x,y and z
z = kxy
k is the cofficient
for x = 7, y = 3 and z = -14
-14 = k*3*7
⇒k = -2/3
for x= 3 and z = -8
-8 = (-2/3)*3*y
y = 4
The equation is z = (-2/3)*xy with of x , y and z are jointly varied.
To learn more about Joint Variation refer to :
https://brainly.com/question/28656799
#SPJ4
Veterinary doctors marked 30 deer on an island and released them. Later on, they counted 150 deer, 12 of which had marks. To the nearest whole
number, what is the best estimate for the deer population for the island?
Answers
The best estimate for the deer population on the island is 500.
1. The veterinary doctors marked 30 deer on the island.
2. Later on, they counted 150 deer in total.
3. Out of the 150 deer, 12 had marks.
4. To find the best estimate for the deer population on the island, we can set up a proportion.
5. Let "x" represent the total deer population.
6. The proportion can be set up as: 30/x = 12/150.
7. Cross-multiplying gives us: 12x = 30 * 150.
8. Solving for x, we get: x = (30 * 150) / 12.
9. Evaluating the expression, we find: x = 375.
10. Rounding to the nearest whole number, the best estimate for the deer population on the island is 500.
For more such questions on population, click on:
https://brainly.com/question/30396931
#SPJ11
pls complete it (picture)

Answers
Answer:
Step-by-step explanation:
the 7cm and the 3cm is 21 cm^2 the 4cm and the 5cm is 20cm^2
the 11cm and the 2cm is 22cm^2
basically if your looking for the largest area then the 11cm and the 2 cm is your answer.
Find the slope of the following graph and write your result in the empty box

Answers
Answer:
The slope is 2.
Step-by-step explanation:
You can use the slope formula or pick two points, count up from one point then to the right. Use rise/run if you use the counting method.
The slope formula is y2-y1/x2-x1
Use the points (20, 20) and (30, 40)
Look at this link to understand how to use it.
https://brainly.com/question/28619876
Hope this helps!
Please mark as brainliest if correct!
Find value of x.
3x + 6 - 6 = 248
Answers
Answer:
The value of x is 82.67Step-by-step explanation:
Q. 3x + 6 - 6 = 248= 3 x = 248= x = 248 / 3 = 82.67∴ The value of x is 82.67
Answer:
x=82.7
Step-by-step explanation:
3x+6-6=248
3x=248
x=82.7
How many triangles exist with the given side lengths?.
Answers
Exactly one unique triangle exists with the given side lengths, option B is correct.
Here, we are given that the three sides of triangle are- 12, 15 and 18.
According to the triangle inequality theorem- “The sum of the length of any two sides of a triangle should be greater than the third side”. Let us see if this holds in this case-
(12 + 15) > 18
(15 + 18) > 12
(12 + 18) > 15
Thus, we see that the triangle inequality theorem is satisfied. So there is only one triangle possible with the sides of given lengths.
Hence, exactly one unique triangle exists with the given side lengths, option B is correct.
Learn more about triangles here-
https://brainly.com/question/17335144
#SPJ4
Your question was incomplete. Check for full content below-
How many triangles exist with the given side lengths?
12 in, 15 in, 18 in
A) No triangle exists with the given side lengths.
B) Exactly one unique triangle exists with the given side lengths.
C) More than one triangle exists with the given side lengths.
11. Find the value of x in the diagram below.

Answers
=====================================================
Explanation:
Points Z and Y are midpoints of segments SR and RQ respectively.
These points form the midsegment ZY.
SQ is twice as long compared to YZ, since the midsegment is half as long as the side parallel to it.
We can then say...
SQ = 2*(YZ)
3x-8 = 2*(x+2)
3x-8 = 2x+4
3x-2x = 4+8
x = 12
DeShawn needs grass seed to cover Field A. One bag of grass seed covers `5\ 000` square feet.
Field A is a circular field with a `100`-foot radius.
What is the fewest number of bags DeShawn must buy to cover Field A?

Answers
The fewest number of bags needed to cover the circular field is 7.
What is the fewest number of bags needed?The first step is to determine the area of the circular field. A circle is a bounded figure which points from its center to its circumference is equidistant.
Area of a circle = πr²
Where :
π = pi = 3.14r = radiusArea of the circular field : 3.14 x 100² = 31,400 feet²
In order to determine the fewest number of bags that can cover the circular field, divide the area of the circular field by the number of square feet one bag can cover.
Fewest number of bags needed = area of the circular field / capacity of one bag
Fewest number of bags needed = 31,400 feet² / 5000 = 6.28 ≈ 7
To learn more about the area of a circle, please check: https://brainly.com/question/14351152
#SPJ1
Evaluate yz + x² x=3.2, y=6.1, z=0.2
Answers
Answer:
Step-by-step explanation:
To evaluate the given expression, we need to substitute the given values for x, y, and z. The expression becomes:
yz + x²
Substituting the given values, we get:
(6.1 * 0.2) + (3.2^2)
This simplifies to:
1.22 + 10.24
Therefore, the value of the expression is approximately 11.46.
11.46
gimme brainlyest gang
How to solve this please

Answers
The value of x, considering the proportional relationship in this problem, is given as follows:
\(x = 0.77 \times 10^{-46}\)
What is a proportional relationship?A proportional relationship is a relationship in which a constant ratio between the output variable and the input variable is present.
The proportional relationship for this problem is given as follows:
1u - \(6.02 \times 10^{23}\)
x u - \(4.65 \times 10^{-23}\)
Applying cross multiplication, the value of x is given as follows:
\(x = \frac{4.65 \times 10^{-23}}{6.02 \times 10^{23}}\)
\(x = 0.77 \times 10^{-46}\)
A similar problem, also featuring proportional relationships, is presented at https://brainly.com/question/7723640
#SPJ1
can u please help ASAP

Answers
Answer:
your question is not complete
A building supply company requires at least 30 pallets of brick weighing 900 pounds each and at least 20 pallets of roofing material each weighing 650 pounds in order to make a delivery. The company's shipping trucks have a load capacity of 34,000 pounds. Express these restrictions with a system of inequalities. Make sure you define your variables. Problem 11. What is the effective interest rate of 8.1% interest compounded monthly? Show how you calculated your answer. Problem 12. If you wanted to estimate the probability that a household in Winona has a Roku hooked up to at least one of the TVs in the house describe what data you would need to collect in order to estimate that probability.
Answers
1. Building Supply Company:
Let's define the variables:
Let B represent the number of pallets of bricks.
Let R represent the number of pallets of roofing material.
According to the problem, we have the following restrictions:
At least 30 pallets of brick: B ≥ 30
Each brick pallet weighs 900 pounds: 900B ≤ 34,000 (load capacity of the truck)
At least 20 pallets of roofing material: R ≥ 20
Each roofing material pallet weighs 650 pounds: 650R ≤ 34,000
The first inequality ensures that the company has at least 30 pallets of bricks.
The second inequality guarantees that the total weight of bricks (900B) does not exceed the load capacity of the truck, which is 34,000 pounds.
The third inequality ensures that the company has at least 20 pallets of roofing material.
The fourth inequality guarantees that the total weight of roofing material (650R) does not exceed the load capacity of the truck.
2. Effective Interest Rate Calculation:
To calculate the effective interest rate compounded monthly, we use the formula:
Effective Interest Rate = (1 + (Annual Interest Rate / Number of Compounding Periods)) ^ Number of Compounding Periods - 1
In this case, the annual interest rate is 8.1% (0.081) and it is compounded monthly. Therefore, we have:
Effective Interest Rate = (1 + (0.081 / 12))^12 - 1 = 8.44%
LEARN MORE ABOUT variables here: brainly.com/question/15078630
#SPJ11
The graph represents the distribution of the lengths of play times, in minutes, for songs played by a radio station over one hour.
A graph shows the horizontal axis numbered 2.6 to x. The vertical axis is unnumbered. The graph shows an upward trend from 2.8 to 3.4 then a downward trend from 3.4 to 4.
Which statement is true about the songs played during the one-hour interval?
Most of the songs were between 3 minutes and 3.8 minutes long.
Most of the songs were 3.4 minutes long.
Most of the songs were less than 3.2 minutes long.
Most of the songs were more than 3.6 minutes long.
Answers
The correct statement is Most of the songs were between 3 minutes and 3.8 minutes long.
Based on the given information from the graph, we can determine the following:
The graph shows an upward trend from 2.8 to 3.4 on the horizontal axis.
Then, there is a downward trend from 3.4 to 4 on the horizontal axis.
From this, we can conclude that most of the songs played during the one-hour interval were between 3 minutes and 3.8 minutes long. This is because the upward trend indicates an increase in length from 2.8 to 3.4, and the subsequent downward trend suggests a decrease in length from 3.4 to 4.
Therefore, the correct statement is:
Most of the songs were between 3 minutes and 3.8 minutes long.
for such more question on minutes
https://brainly.com/question/25279049
#SPJ8
Answer:
A
Step-by-step explanation:
Someone help please

Answers
what are the coordinates of the vertex of the parabola shown (90,50) (10,50) (10,700) (50,700)

Answers
The vertex of a parabola is the point at the intersection of the parabola and its line of symmetry.
The vertex of a parabola is the point at the
intersection of the parabola and its line of symmetry
Given the line 2x – 3y = 9 and the point (4, –1), find lines through the point that are
(a) parallel to the given line and
(b) perpendicular to it.
Answers
We will find the parallel line:
y = (2/3)*x - 11/3
And the perpendicular line:
y = (-3/2)*x + 5
How to find the two linear equations?Here we start with the linear equation, we will get:
2x - 3y = 9
We can rewrite it to get:
-3y = 9 - 2x
y = 9/-3 - 2x/-3
y = -3 + (2/3)x
Remember that two lines are parallel if the lines have the same slope, so the equation of the parallel line will be something like:
y = (2/3)*x + b
And this line must pass through (4, -1), replacing these values we will get:
-1 = (2/3)*4 + b
-1 = 8/3 + b
-1 - 8/3 = b
-3/3 - 8/3 = b
-11/3 = b
So the linear equation parallel is:
y = (2/3)*x - 11/3
Now let's find the perpendicular line. Remember that two lines are perpendicular if the product between the slopes is equal to -1, then if the slope of the perpendicular line is m, we need to solve:
m*(2/3) = -1
m = -3/2
Then the perpendicular line is something like:
y = (-3/2)*x + b
To find te value of b, we need to replace the values of the point (4, -1) there, we will get:
-1 = (-3/2)*4 + b
-1 = -6 + b
-1 + 6 = b
5 = b
So the perpendicular line is:
y = (-3/2)*x + 5
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
Please Help 100 POINTS!!!

Answers
Answer:
B
Step-by-step explanation:
Answer:
B. \(\frac{x^2}{3^2} +\frac{y^3}{2^2} =1\)
Step-by-step explanation:

Open Ended You are given the point Q(-2, -5).
A. Identify a point (X1, Y1,) that along with point Q defines a line with a
positive slope.
B. Identify a point (X2, Y2) that along with point Q defines a line with a
negative slope.
Answers
The point that defines a line with positive slope to point Q(-2, -5) is (0, 0)
The point that defines a line with negative slope to point Q(-2, -5) is (1, 7)
How to find points with positive and negative slopeslope, m is calculated from the formula
m = (y₀ - y₁) / (x₀ - x₁)
The slope, m calculating using the point (-2, -5) and (X1, Y1) = (0, 0)
m = (0 - -5) / (0 - -2)
m = (5) / (2)
m = 5/2
the point from origin gave a positive slope
The slope, m' calculating using the point (-2, -5) and (X2, Y2) = (1, -7)
m' = (-7 - -5) / (1 - -2)
m = (-12) / (3)
m = -4
the point from (1, -7) gives a negative slope
Learn more about slope of linear functions at:
https://brainly.com/question/29323505
#SPJ1
Make a stem-and-leaf plot for each set of data.
68, 73, 66, 76, 86, 74, 61, 89, 65, 90
136, 142, 105, 147, 126, 109, 118, 111, 129, 115, 128, 138
Answers
stem-and-leaf plots for the sets of data are attached.
What is stem-and-leaf plot?
In a stem and leaf plot, the values of the data are divided into a stem and a leaf, creating a singular table. The initial digit or digits are written in stem format, and the final digit is written in leaf format.
Data can be arranged in a way that makes it simple to see the frequency of various sorts of values using a stem and leaf plot, also known as a stem and leaf diagram. It is a graph with numerical data displayed in a sequential manner. Each value of the data is divided into a stem and a leaf.
A stem and leaf plot is depicted as a customised table with each data value's initial or last digit divided into a stem and the leaf's final digit.
To learn more about the stem-and-leaf plot from the given link
https://brainly.com/question/29740594
#SPJ1


When data are positively skewed, the mean will usually be:
a. greater than the median
b. smaller than the median
c. equal to the median
d. positive
Answers
When data are positively skewed, the mean will be greater than the median.
This is because the mean will be pulled in the direction of the higher values in the data set, while the median will ignore the higher values and be more affected by the lower values in the data set.
Positively skewed data is characterized by a long tail on the right side of the distribution graph. This means that the data set contains more values that are higher than the mean and median. As a result, the mean will be a higher value than the median, as the mean will be pulled in the direction of the higher values. The median, however, will remain unaffected by the higher values and will be more affected by the values at the lower end of the distribution.
the complete question is :
When data are positively skewed, the mean will usually be:
a. greater than the median
b. smaller than the median
c. equal to the median
d. positive or negative depending on the data set
Learn more about median here
https://brainly.com/question/15323584
#SPJ4
Find the point on the graph of y=x^2 where the curve has slope m= -1/5 The point on y=x^2 at which the tangent line has slope -1/5 is ___ (Type an ordered pair. Use integers or fractions for any numbers in the expression.)
Answers
the points are (0, 0) and (-5/7, 25/49).The ordered pair, in this case, is: (-5/7, 25/49).
To determine the point on y=x² at which the tangent line has slope -1/5, use the following steps;The slope of the curve at x is given by y' = 2x.The equation of the tangent line at (x, y) is given by y-y = m(x-x), where m is the slope of the tangent line; y-y = (-1/5)(x-x)On substituting for y, y' and m, the equation of the tangent line becomes x-2y = -5x/5-7y = -5xOn substituting y = x², the equation becomes;7x² + 5x = 0Factor x out,7x(x + 5/7) = 0Then x = 0 or x = -5/7,
To know more about, tangent visit
https://brainly.com/question/19064965
#SPJ11
Answer: The point on the graph of y = x² where the curve has slope m= -1/5 is (-1/10, 1/100).
Hence, the required solution is (-1/10, 1/100).
Step-by-step explanation: Given that, the slope of the tangent line is -1/5 and we need to find the point on the graph of y = x² where the curve has slope m= -1/5.
So, let's solve the given problem and find the solution:
We have the equation of the curve:
y = x²
Differentiate the above equation with respect to x to find the slope of the curve, and we get:
dy/dx = 2x
Since we need to find the slope of the curve when y = x², we can equate dy/dx to
m=-1/5.-1/5
= 2x
So, x = -1/10 When x = -1/10, we have
y = (-1/10)²
= 1/100
To know more about slope visit:
https://brainly.com/question/3605446
#SPJ11
Find the value(s) of c guaranteed by the mean value theorem for integrals for the function over the given interval. (round your answer to four decimal places. Enter your answers as a comma-separated list. ) f(x) = 2 x , [4, 9].
Answers
The value of c will be 0, for the given function f(x) = 2x
What is mean value theorem?
The mean value theorem asserts that there is at least one point on the curve (c, f(c)) where the tangent is parallel to the secant going through the two supplied points for every function f(x) whose graph goes through the two given locations (a, f(a)), and (b, f(b)). Here, the calculus definition of the mean value theorem is given for the function f(x): [a, b] R, which is continuous and differentiable over an interval.
Given f(x) = 2x
f(4) = 8
f(9) = 18
We can write f '(c) = \(\frac{f(9)-f(4)}{9-4}\)
=\(\frac{18-8}{5}\)
=\(\frac{10}{5}\)
=\(2\)
We can find the derivative of f ' (x) = 2
As it is independent of x, so the term c = 0
Hence, the value of c will be 0.
Learn more about mean value theorem, by the following link.
https://brainly.com/question/17111829
#SPJ4
You start a bacterial colony and notice that it quadruples each day. What does the term 65 mean in the exponential function y=65*4^x?

Answers
=======================================================
Reason:
The start point occurs at x = 0, since negative time values do not make sense. In other words, a negative number of days isn't possible.
Plug x = 0 into the function to find that...
y = 65*4^x
y = 65*4^0
y = 65*1
y = 65
Recall that raising any nonzero number to the zeroth power gives 1 (i.e. x^0 = 1 where x is any number but zero)
We've shown that x = 0 leads to y = 65.
That number out front (65) is the amount of bacteria at the start, to confirm the answer above.
In general, y = a*b^x will have "a" as the starting amount. We have a = 65 and b = 4 in this case. The "b" term is tied closely to the growth rate.
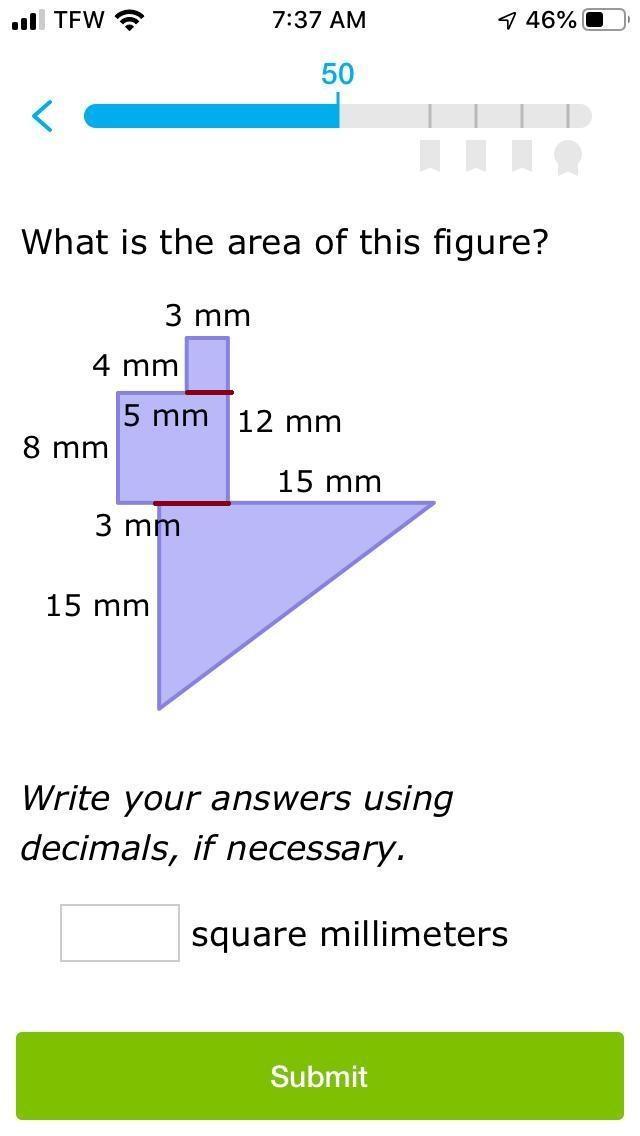
Can someone answer this question please please help me I really need it if it’s correct I will mark you brainliest .

Answers
Answer:
As I divided in the picture,
Total area = area of triangle + area of 2 rectangles
= base x height/2 + length1 x width1 + length2 x width2
= 15 x (15 + 3 + 5 - 3)/2 + 3 x 4 + 8 x (3 + 5)
= 226
Hope this helps!
:)
A ball is launched from a 25.48-meter tall platform. The equation
for the ball's height h at time t seconds after launch is h (t) =
-4.9t2 +20.58t + 25.48, where his in meters. What is the
maximum height the ball achieves before landing?
Answers
Answer:
\(\boxed{47.089 \;meters} \\\\\)
Step-by-step explanation:
For any function f(x), the maximum or minimum value can be determined by 1. Finding the first derivative f(x) with respect to x i.e. f'(x)
2. Setting this first derivative to 0, solving for x
3. Substituting for x in the original function to get the maximum/minimum value
\(\textrm{The equation for the function f(t) is }\\f(t) = -4.9t^2 + 20.58t + 25.48\\\\\)
\(\textrm{The first derivative of this function with respect to t is }\\\\f'(t) = - 2\cdot 49t + 20.58\\= -9.8t + 25.48\\\\\)
\(\textrm{Setting this first derivative equal to 0 gives:}\\\\-9.8t + 20.58 = 0\\\\-9.8t = -20.58 \;\;\;\;\;\textrm{(Subtracting 20.58 from both sides)}\\\\9.8t = 20.58 \;\;\;\;\;\; \textrm{ (Multiplying both sides by -1)}\)
\(\textrm{Therefore }\\\\t = \dfrac{20.58}{9.8}\\\\t= 2.1 \textrm{ seconds}\)
\(\textrm{Therefore, at = 2.1 seconds, the ball will reach its maximum height.}\)
To find what this maximum height is, substitute t = 2.1 in the original equation and solve for h(t)
\(h(t)\;at\;t=2.1 \\h(2.1) = 4.9\cdot \:2.1^2+20.58\cdot \:2.1+25.48=47.089 \;meters\\\\\)
\(\textrm{ The maximum height the ball achieves before landing is } \boxed{47.089 \;meters} \\\\\)
\(\textrm {This occurs 2.1 seconds after launch }\)