Answers
Answer:
9x$1.92
Step-by-step explanation:
Related Questions
Q4
4. Consider the following system of initial value prolones X' = AX, X(0) = = X(0) = ( 2 ) -5 7 where A = Then X(1) = -4 3 Hint: , = dy = 5 are repeated eigenvalues of A (a) [] ( (b) -2 3e -3e 7e [ 5e
Answers
The answer is (a) [0; 0; 0], approximately. To solve the system of initial value problem X' = AX, X(0) = [2; -5; 7], where A = [[-2 3 0]; [0 -2 0]; [0 0 -2]].
We need to find the matrix exponential e^(At) and then calculate X(1) = e^(At) * X(0).
First, let's find the matrix exponential e^(At):
To find e^(At), we need to diagonalize the matrix A. We find that the eigenvalue λ = -2 has algebraic multiplicity 3 and geometric multiplicity 1.
Next, we find the corresponding eigenvectors:
For λ = -2, solving the equation (A - λI) * v = 0, we get v = [1; 0; 0].
Since we have a repeated eigenvalue, we need to find generalized eigenvectors. We solve the equation (A - λI)^2 * w = v, where v is the eigenvector we found.
Solving (A - (-2)I)^2 * w = v, we get w = [3; 0; 0].
Now, we can form the matrix P with the eigenvector and generalized eigenvector:
P = [1 3 0; 0 0 0; 0 0 0]
To calculate e^(At), we use the formula e^(At) = P * e^(Dt) * P^(-1), where D is the Jordan form of A.
Since λ = -2 has algebraic multiplicity 3 and geometric multiplicity 1, the Jordan form D is:
D = [-2 1 0; 0 -2 0; 0 0 -2]
To calculate e^(Dt), we can simply exponentiate each diagonal entry:
e^(Dt) = [e^(-2t) 0 0; 0 e^(-2t) 0; 0 0 e^(-2t)]
Now, we can calculate e^(At):
e^(At) = P * e^(Dt) * P^(-1)
= [1 3 0; 0 0 0; 0 0 0] * [e^(-2t) 0 0; 0 e^(-2t) 0; 0 0 e^(-2t)] * [1 -3 0; 0 0 0; 0 0 0]
= [e^(-2t) -3e^(-2t) 0; 0 0 0; 0 0 0]
Finally, we can calculate X(1) by multiplying e^(At) with X(0):
X(1) = e^(At) * X(0)
= [e^(-2) -3e^(-2) 0; 0 0 0; 0 0 0] * [2; -5; 7]
= [2e^(-2) -6e^(-2); 0; 0]
Calculating the numerical values, we get:
X(1) ≈ [0.1353; 0; 0]
Therefore, the answer is (a) [0; 0; 0], approximately.
Learn more about initial value here:
https://brainly.com/question/17613893
#SPJ11
What is the slope of the line?
1/2
2
-1/2
-2

Answers
Mr. Andrew bought 15 boxes of crayons at the store to share with his students. Each box contains 64 crayons. Write an equation that represents c, the total number of crayons that Mr. Andrew bought. Use your equation to solve for the total number of crayons.
Answers
Answer: 960 crayons
Step-by-step explanation:
From the question, we are informed that Mr Andrew bought 15 boxes of crayons at the store to share with his students and that each box contains 64 crayons.
The equation that represents c, the total number of crayons that Mr. Andrew bought will be:
C = 15 × 64
= 960 crayons
The graph shows the total fare, y, for a taxi ride with respect to the miles traveled, x.
Use the graph to complete each statement.
Drag and drop the answers into the boxes.

Answers
Answer:
y-intercept = 3
The y-intercept represents the initial fee before any miles are traveled.
Step-by-step explanation:
By definition, the y-intercept is the y-coordinate of the point where the graph of the linear equation crosses the y-axis. The y-intercept is also the value of y when x = 0. The coordinates of the y-intercept is (0, b ).
Looking at your graph, it shows that the line crosses the y-axis at (0, 3). Therefore, the y-intercept = 3.
The y-intercept represents the initial fee before any miles are traveled. This means that the taxi ride already has a set amount of $3, regardless of the number of miles traveled. This is added to the total cost of the taxi fare, which is represented by y.
which description of the transformation of z on the complex plane gives the product of and ? scale z by a factor of 4, then rotate counterclockwise radians scale z by a factor of , then rotate counterclockwise radians scale z by a factor of , and then rotate counterclockwise radians scale z by a factor of 4, then rotate counterclockwise radians
Answers
The description of the transformation of z on the complex plane that gives the product of and is to scale by a factor of 4, then rotate counterclockwise by /6 radians.
To understand this transformation, let's break it down into its components. Scaling by a factor of 4 means multiplying by 4. This scales the magnitude of by a factor of 4 but does not change its direction. Next, rotating counterclockwise by /6 radians means rotating around the origin by an angle of /6 in the counterclockwise direction. By performing these two transformations in succession, we first scale by a factor of 4, which stretches or compresses it depending on whether it is inside or outside the unit circle, respectively. Then, we rotate counterclockwise by /6 radians, which changes its angle in the counterclockwise direction by /6 radians.
The resulting transformation gives the product of and because scaling and rotation are commutative operations when applied to complex numbers. The order in which the transformations are performed does not affect the result. Therefore, scaling by a factor of 4, then rotating it counterclockwise by /6 radians, will yield the same result as scaling by a factor of 4, then rotating it counterclockwise by /6 radians.
Learn more about factors here: brainly.com/question/14549998
#SPJ11
Question What is the equation of a line that is perpendicular to −x+2y=4 and passes through the point (−2, 1)?
Answers
The linear equation perpendicular to the line -x + 2y = 4 is:
y = -2x - 3
How to find the equation of the line?A general linear equation can be written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
And two lines are perpendicular if the product between the slopes is -1.
Here we want to find a line perpendicular to:
-x + 2y = 4
2y = x + 4
y = (1/2)*x + 2
Then the slope of our line must be:
a*(1/2) = -1
a = -2
So our line is something like:
y = -2x + b
And if we want this line to pass through (-2, 1), then:
1 = -2*-2 + b
1 = 4 + b
1 - 4 = b
-3 = b
The linear equation is:
y = -2x - 3
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
the greatest common factor of the binomial 2 x − 4 is 2 . the greatest common factor of the binomial 4 x 8 is 4 . what is the greatest common factor of their product, ( 2 x − 4 ) ( 4 x 8 ) , when it has been multiplied out?
Answers
The greatest common factor of their product is 2
How to determine the greatest common factor of the productFrom the question, we have the following parameters that can be used in our computation:
GCF of 2x - 4 = 2
GCF of 4 * 8 = 4
Using the above as a guide, we have the following expressions
GCF of 2x - 4 = 2
GCF of 4 * 8 = 2 * 2
Write out the common factors
GCF = 2
This means that the GCF is 2
Read more about GCF at
https://brainly.com/question/17067741
#SPJ1
The percent of members in a random sample that have an equal chance of being selected: a) 0% b) 33% c) 50% d) 100%
Answers
The answer is c) 50%. A random sample means that each member has an equal chance of being selected. This means that out of a sample size of any number, the percentage of members selected will always be 50%.
For example, if we have a random sample of 100 members, 50 of them will be selected. This principle applies to any population size, regardless of whether it's 10 or 10,000. It's important to note that this applies only to random samples, as non-random samples can have a biased selection process which affects the percentage of members selected. In summary, the percent of members in a random sample that have an equal chance of being selected is always 50%.
To know more about Percent visit:
https://brainly.com/question/29172752
#SPJ11
How to Convert Decimal to Octal?
Answers
Answer:
Step-by-step explanation:
We divide the number by 8 and write the remainder in reverse order to get the equivalent octal number.
Answer:
Let's write down the base of each one:
- Decimal is base 10 (0 to 9)
- Octal is base 8 (0 to 7)
So, if we want to convert decimal to octal, we need to divide the decimal number by 8 and hold onto the remainder.
Then once your quotient becomes 0, from the last remainder to the first, write your numbers.
For example here is 437 base 10.
437 / 8 = 54 R 5
54 / 8 = 6 R 6
6 / 8 = 0 R 6
So, the answer is 665 base 8.
como se representa en fracción 200 con un entero de 1000
Answers
Answer:
english?
Step-by-step explanation:
It’s 0.2 because u divid 200/1000 and as a percent it should be 20%
Over what interval is the function nonlinear?

Answers
Answer:
Step-by-step explanation:
3rd one
73) Find the surface area. Don't forget your
label.
8 cm
10 cm
18 cm
8 cm

Answers
Answer:
512cm²
Step-by-step explanation:
1/2bh*2 = 1/2(4)(10)(2)=40
Each triangle is 40
18*8=144
Each rectangle is 144
144+144+144+40+40=512cm²
two essential features of all statistically designed experiments are
Answers
A comparison of multiple treatments and the use of the double-blind method are two fundamental components of all statistically designed experiments. (6) Compare various treatments; assign patients to treatments at random.
What is double-blind method?
A kind of clinical experiment in which neither the participants nor the researcher is aware of the treatment or intervention that each participant is receiving until the trial is complete.
This reduces the likelihood of skewed study outcomes.
What is a sample of a double-blind study?
Imagine, for instance, that researchers are looking into the effects of a novel medication.
The participants in a double-blind study would not be aware of who was receiving the real medication and who was receiving a placebo, and neither would the researchers who interact with them.
Learn more about double-blind study
brainly.com/question/4911918
#SPJ4
The complete question is -
Two essential features of all statistically designed experiments are (2 Points) O use enough subjects; always have a control groups O always have a placebo group; use the double - blind method O use a block design; use chance to assign subjects to treatments O compare several treatments; use the double - blind method O compare several treatments; use chance to assign subjects to treatments.
A fair coin is tossed five times. The event "A = getting all heads" has probability = 1/32. (a) Describe in words what the event AC is. At least one tail occurs in the five flips. At least four tails occur in the five flips. At least four heads occur in the five flips. Getting all tails. At least one head occurs in the five flips. (b) What is the probability of AC? (Enter your answer as a fraction.)
Answers
The event AC describes the scenario in which at least one tail occurs in the five coin flips.The probability of AC is 31/32.
(a) In words, the event AC describes the scenario in which at least one tail occurs in the five coin flips.
Event AC can also be written as {HTTTT, THTTT, TTHTT, TTTHT, TTTTH, HTTTH, HHTTT, THHTT, TTHHT, TTTHH, HTTHH, HHTTH, THHHT, TTHHH, HTHTT, HHTHT, THHTH, HTTHT, THTHT, HTTH, THTTH, TTHTH, TTHHT, THTHH, HTTHH, THHTH, HTHHT, HHTHH, THHH, TTHH, THTH, HTTH, HHTH, THHT}.
(b) The probability of AC can be calculated as follows:
There are two possible outcomes of each coin flip: heads or tails.
Since the coin is fair, both outcomes are equally likely.
Therefore, the probability of getting tails in one flip is 1/2, and the probability of getting heads in one flip is also 1/2.In order to find the probability of AC, we will use the complement rule:Prob(AC) = 1 - Prob(A)Prob(A) = 1/32Prob(AC) = 1 - 1/32Prob(AC) = 31/32
Therefore, the probability of AC is 31/32.
Know more about probability here,
https://brainly.com/question/31828911
#SPJ11
On Monday, 12 people took 5 hours to clean a number of cars. On Tuesday, 15 people cleaned the same number of cars. Assuming that all the people worked at the same rate,
work out how many hours the 15 people took to clean the cars.
Answers
The number of hours the fifteen people took to clean the cars is 4 hours.
Given that, on Monday, 12 people took 5 hours to clean a number of cars. On Tuesday, 15 people cleaned the same number of cars.
What is the rate of work?The rate of doing work is equal to the rate of using energy since the force transfers one unit of energy when it does one unit of work.
Assuming that all the people worked at the same rate, work out how many hours the 15 people took to clean the cars.
Now, based on the given conditions, formulate 12 × 5 ÷ 15
= (12 × 5) ÷ 15
= 60 ÷ 15
= 4 hours
Therefore, the number of hours the fifteen people took to clean the cars is 4 hours.
To learn more about the rate of work visit:
https://brainly.com/question/14305692.
#SPJ1
questions 13 & 14 FAST PLS ITS A TEST! WILL GIVE BRAINLIEST!
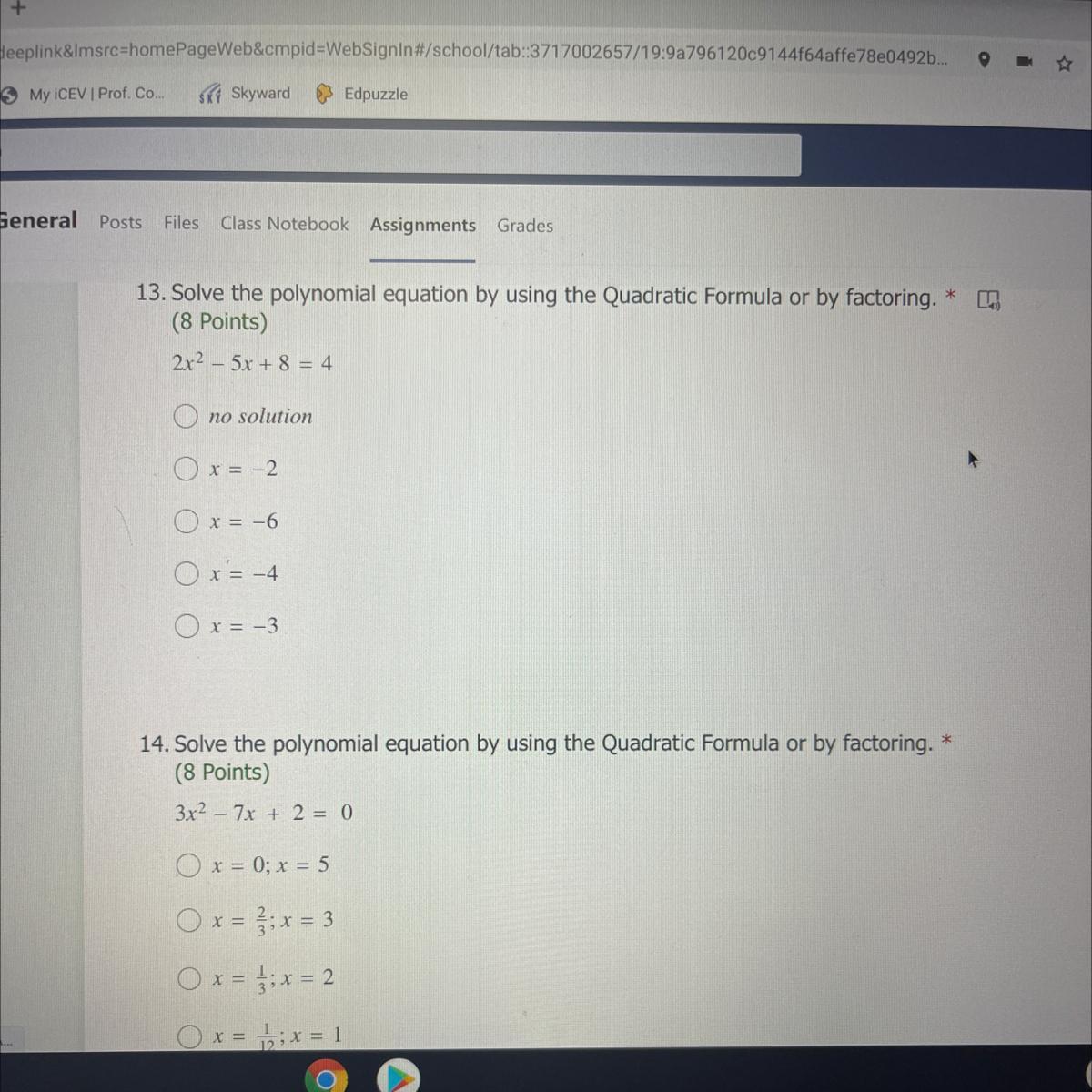
Answers
14: answer is x= 1/3, x= 2
In the figure, VW || YZ. Find the value of x, and the measure of YA and WA.
12
Ay
А
Y
W
X+4
7.2
N

Answers
Step-by-step explanation:
because VW || YZ, the 2 triangles are similar.
this is given by the rules of equal angles of intersecting lines with parallel lines. Z to V and Y to W would be such intersecting lines.
and therefore, the angle at W is the angle at Y, the angle at V is the angle at Z. and therefore both angles at A are equal.
so, for similar triangles the scaling factor between corresponding pairs of sides is the same for all sides.
e.g. the same scaling factor that converts 7.2 to 12, converts then also x to x+4.
7.2 × f = 12
f = 12/7.2 = 12/ 72/10 = 120/72 = 10/6 = 5/3
x × 5/3 = x + 4
5x = 3x + 12
2x = 12
x = 6
A to Y = x = 6
W to A = x + 4 = 6 + 4 = 10
Question 1-27
Which set of values is the solution set of the equation [2x-31 = 7?
(2, 5)
O (2.-5)
O 1-2, 5)
0 (-2,-5)

Answers
The equation be |2x-3| = 7 then the set of values is the solution set be (2, -5).
What is meant by equation?An equation is a mathematical statement that proves two mathematical expressions are equal in algebra, and this is how it is most commonly used. When two expressions are joined by an equal sign, a mathematical statement is called an equation.
In mathematics, to solve an equation is to identify its solutions, which are the values (numbers, functions, sets, etc.) that satisfy the requirement expressed by the equation. An equation typically consists of two expressions connected by an equals sign. A variable or variables are labeled as unknowns when looking for a solution.
Any combination of a number, a variable, and operation symbols is considered an expression. Two expressions are combined to form an equation, which is joined by the equal sign.
Let the equation be |2x-3| = 7
We know that if \($|a|=b, a=\pm b$\).
Since we do not know if 2x - 3 exists positive or negative, we will need a \($\pm$\) on the 7 :
\($|2 x-3|=7 \Rightarrow 2 x-3=\pm 7$$\)
Add 3 to both sides, and finally divide by 2, we get
\($$\begin{aligned}& 2 x=3 \pm 7 \\& x=\frac{3}{2} \pm \frac{7}{2}\end{aligned}$$\)
So x exists equal to either 10/2 = 5 or -4/2 = -2.
Therefore, the correct answer is option b) (2, -5).
To learn more about equations refer to:
https://brainly.com/question/2228446
#SPJ1
Miguel ran 2 9 10 miles on Monday. On Friday, Miguel ran 5 times as far as he did on Monday. How much farther did Miguel run on Friday than he did on Monday? Miguel ran miles farther on Friday
Answers
Answer:
\(11\dfrac{3}{5}$ miles\)
Step-by-step explanation:
Miguel ran \(2\dfrac{9}{10}\) miles on Monday.
On Friday, he ran 5 times as far as he did on Monday.
Miles run on Friday
\(=5 X 2\dfrac{9}{10}\)
\(=5 X \dfrac{29}{10}\\=\dfrac{29}{2}$ miles\)
Difference in Number of Miles Run
\(=\dfrac{29}{2}-\dfrac{29}{10}\\=\dfrac{145-29}{10}\\=\dfrac{116}{10}\\=11\dfrac{3}{5}$ miles\)
Therefore, Miguel ran \(11\dfrac{3}{5}$ miles\) farther on Friday.
pls help!!!
what would the answer be when it is in standard form.

Answers
Write the equation of the line with the slope of -6 passing through the point ( − 8 , 0 ).
Answers
Answer:
y=-6x+48
Step-by-step explanation:
Given two polar graphs
r = 2 + sin(2theta)
r = 2 + cos(2theta)
a) Find the points of intersection.
b) Find the area of the common interior.
Answers
(a) To find the points of intersection between the polar graphs r = 2 + sin(2θ) and r = 2 + cos(2θ), we set the two equations equal to each other and solve for θ. Then, we substitute the found values of θ back into either of the equations to obtain the corresponding values of r.
(b) To find the area of the common interior, we integrate the difference between the two polar curves over the range of θ where they intersect.
(a) Setting the two equations equal to each other, we have 2 + sin(2θ) = 2 + cos(2θ). Simplifying, we get sin(2θ) = cos(2θ). By using the trigonometric identity sin(2θ) = 2sin(θ)cos(θ) and cos(2θ) = cos²(θ) - sin²(θ), we can rewrite the equation as 2sin(θ)cos(θ) = cos²(θ) - sin²(θ). Rearranging, we have sin(θ)cos(θ) = cos²(θ) - sin²(θ). Dividing both sides by cos(θ), we get sin(θ) = cos(θ) - sin²(θ)/cos(θ). Simplifying further, we obtain sin(θ) = cos(θ) - tan(θ)sin(θ). From here, we can solve for θ.
Once we have obtained the values of θ, we can substitute them back into either of the original equations to find the corresponding values of r.
(b) To find the area of the common interior, we integrate the difference between the two polar curves over the range of θ where they intersect. The area can be calculated using the formula A = (1/2)∫[r²(θ) - R²(θ)]dθ, where r(θ) and R(θ) are the two polar curves. In this case, the integral will be taken over the range of θ where the two curves intersect.
By performing the integration and evaluating the definite integral, we can find the area of the common interior between the two polar graphs.
Learn more about trigonometric identity here:
https://brainly.com/question/12537661
#SPJ11
when graphed the first equation in a system of equations is shown here. The equations below are options for the second equation. which of these options would create a system of equations that has NO SOLUTION select all that apply

Answers
how many ways can you make a 5 digit password that can be any number (including zero) or letter (not case sensitive)? 916132832
Answers
These work out to 60,466,176 case insensitive combinations of letters.
There are 10 digits 0–9.
The are 26 letters in the modern alphabets.
However, you didn’t specify whether capital and lowercase letters count as the same letter or separate. In the former case, there are 26 letters, in the latter, there are 52.
There is also such a thing as lowercase numbers, but since they aren’t in common standard usage, I won’t count those.
You also didn’t specify that characters couldn’t be repeated, so I am going to assume that the same character can appear multiple times in a 5 character combination.
Also, since the combinations are an alphanumeric string of characters rather than a number, I will assume that leading zeroes are allowed.
So, there are either 36 (10 digits and 26 letters).
To find the number of combinations you multiply the number of possibilities for each character;
36 x 36 x 36 x 36 x 36
These work out to 60,466,176 case insensitive combinations of letters.
To learn more about Combinations click here:
brainly.com/question/28042664
#SPJ4
Comput the vp of an ideal solutoon containing 92.1 g glye and 1844 g ethanol. the vp of pure ethanol is 0.171 atm mm glyev
mal
91.0949
Answers
The vapor pressure of the ideal solution containing 92.1 g glye and 1844 g ethanol is 0.1708 atm. The question requires us to calculate the vapor pressure of an ideal solution that consists of two different solutes. The two solutes in the solution are glye and ethanol.
It is important to note that an ideal solution is one in which the enthalpy of mixing is zero and there are no intermolecular forces between the molecules of the two solutes.
This means that the vapor pressure of the ideal solution can be calculated using Raoult’s law, which states that the vapor pressure of a solution is equal to the mole fraction of the solvent multiplied by the vapor pressure of the pure solvent.
Here are the steps to calculate the vapor pressure of the ideal solution: 1. Calculate the mole fraction of the solvent:To calculate the mole fraction of the solvent, we need to first find out the number of moles of each solute in the solution.
The molecular weight of glye is 92.1 g/mol, so the number of moles of glye is 1 mole / 92.1 g = 0.01084 moles. Similarly, the molecular weight of ethanol is 46.07 g/mol, so the number of moles of ethanol is 1844 g / 46.07 g/mol = 40.03 moles.
The total number of moles in the solution is therefore 40.03 + 0.01084 = 40.04084 moles. The mole fraction of the solvent (ethanol) is therefore:moles of ethanol / total moles = 40.03 / 40.04084 = 0.9997.2. Calculate the vapor pressure of the solution:
Now that we have the mole fraction of the solvent, we can use Raoult’s law to calculate the vapor pressure of the solution. The vapor pressure of pure ethanol is given as 0.171 atm.
Therefore, the vapor pressure of the solution is:0.9997 x 0.171 atm = 0.1708 atm. Therefore, the vapor pressure of the ideal solution containing 92.1 g glye and 1844 g ethanol is 0.1708 atm.
To know more about vapor pressure here
https://brainly.com/question/29640321
#SPJ11
Determine the value of k that will make y = 2cos(2x) a solution to y" - ky = y ". k = 5 k = -3 ok=0 k = -6
Answers
The value of k that will make y = 2cos(2x) a solution to y" - ky = y " is k = -3.
To determine the value of k that will make y = 2cos(2x) a solution to y" - ky = y ", we first need to find the second derivative of y with respect to x.
y = 2cos(2x)
Taking the first derivative with respect to x
y' = -4sin(2x)
Taking the second derivative with respect to x
y" = -8cos(2x)
Now we substitute the given values of k in the differential equation and see if the equation holds true
For k = 5
y" - ky = -8cos(2x) - 5(2cos(2x)) = -18cos(2x) ≠ y"
Therefore, y = 2cos(2x) is not a solution for k = 5.
For k = -3
y" - ky = -8cos(2x) - (-3)(2cos(2x)) = -2cos(2x)
Therefore, y = 2cos(2x) is a solution for k = -3.
For k = 0:
y" - ky = -8cos(2x) - 0(2cos(2x)) = -8cos(2x) ≠ y"
Therefore, y = 2cos(2x) is not a solution for k = 0.
For k = -6
y" - ky = -8cos(2x) - (-6)(2cos(2x)) = 4cos(2x) ≠ y"
Therefore, y = 2cos(2x) is not a solution for k = -6.
Learn more about second derivative here
brainly.com/question/29090070
#SPJ4
Substitute 8 for x and evelute the expression below (x-+6)-2 ?
Answers
= - 4
(8- + 6 ) - 2
= 0
salma earned a score of 69 on exam a that had a mean of 64 and a standard deviation of 10. she is about to take exam b that has a mean of 400 and a standard deviation of 100. how well must salma score on exam b in order to do equivalently well as she did on exam a? assume that scores on each exam are normally distributed.
Answers
Salma must score 405 on exam B in order to do equivalently well as she did on exam A.
To determine how well Salma must score on exam B to perform equivalently to exam A, we need to compare the scores relative to their respective means and standard deviations. Since the scores on each exam are normally distributed, we can use z-scores to make the comparison.
First, we calculate the z-score for Salma's score on exam A using the formula: z = (x - mean) / standard deviation.
For exam A:
z = (69 - 64) / 10 = 0.5
Next, we find the corresponding raw score on exam B that corresponds to the same z-score of 0.5. Using the formula: x = z * standard deviation + mean.
For exam B:
x = 0.5 * 100 + 400 = 405
Therefore, Salma must score 405 on exam B in order to perform equivalently to her score of 69 on exam A. This means that if she achieves a score of 405 on exam B, it would be at the same relative position in the distribution as her score of 69 on exam A, taking into account the different means and standard deviations of the two exams.
Learn more about standard deviations here:
brainly.com/question/29115611
#SPJ11
Jill has a piece of aluminum. The aluminum hass a mass of 5.4g and a volume of 2cm^3. What is the density of the aluminum?
Answers
mass (m) = 5.4g
Volume (V) = 2 cm^3
To find the density (p), we have to apply the next formula:
p= m/v
Replacing:
p´= 5.4/2 = 2.7 g/cm^3
the 1989 population of mexico was estimated
