Differentiate the following equation \(sin^2(\frac{\pi }{6} -x)\)
Answers
\(\sin^2\left(\frac{\pi }{6}-x \right)\implies \left[ ~~ \sin\left(\frac{\pi }{6}-x \right) ~~ \right]^2 \\\\\\ \stackrel{\textit{\LARGE Chain Rule}}{2\left[ ~~ \sin\left(\frac{\pi }{6}-x \right) ~~ \right]^1 \left[ ~~ \cos\left(\frac{\pi }{6}-x \right) ~~ \right] (-1)}\implies \boxed{-2\sin\left(\frac{\pi }{6}-x \right)\cos\left(\frac{\pi }{6}-x \right)}\)
Related Questions
Fill in the blanks below.
Find the slope of the line passing through the points (7, 7) and (7-8).
slope:
Find the slope of the line passing through the points (-6, 7) and (9,7).
slope:
Answers
Answer:
a) Slope of the line m = ∞
b) Slope of the line m =0
Step-by-step explanation:
Explanation:-
Step(i):-
Given points are ( 7,7) and (7,-8)
Slope of the line
\(m = \frac{y_{2} - y_{1} }{x_{2}-x_{1} }\)
\(m = \frac{-8-7 }{7-7 } = \frac{-15}{0} = infinite\)
m = ∞
Step(ii):-
Given points are (-6,7) and (9,7)
Slope of the line
\(m = \frac{y_{2} - y_{1} }{x_{2}-x_{1} }\)
\(m = \frac{7-7 }{9-(-6) } = \frac{0}{15} = 0\)
Slope of the line m =0
Using the Distributive Property, Solve the Problem below:
-2.5(4x - 4) = -6
(After using the Distributive Property, Solve for x)
Answers
The solution of the given linear equation can be obtained as x = 0.4.
What is meant by the distributive property?The distributive property states that the product of a number and the sum of other numbers is equal to the sum of their individual products.
It can be expressed as a(b + c + d) = ab + ac + ad.
The given linear equation can be solved as follows,
-2.5(4x - 4) = -6
Use distribute property in the RHS to obtain,
-2.5 × 4x - 2.5 × -4 = 6
=> -10x + 10 = 6
=> -10x = -4
=> x = 0.4
Hence, the given equation can be solved as x = 0.4.
To know more about linear equation click on,
https://brainly.com/question/11897796
#SPJ1
someone, please help this is due soon if you can explain them I really appreciate it (PICTURE) 15 points and brainliest.
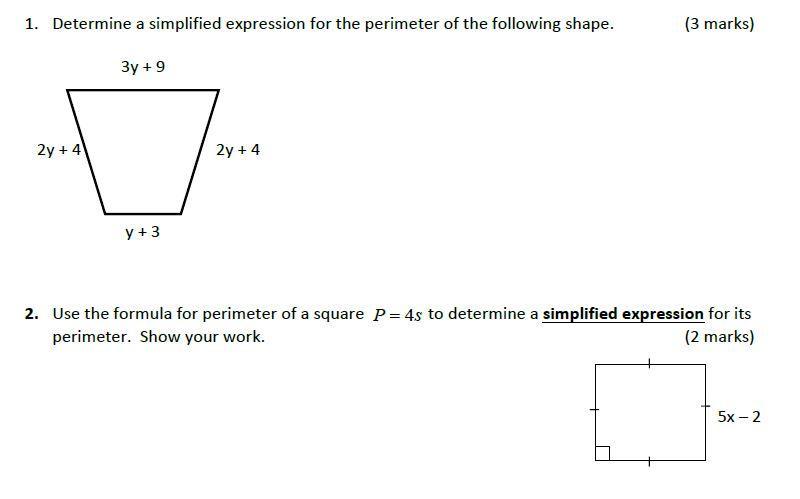
Answers
Step-by-step explanation:
1. Given,
Sides of the shape = 3y+9, 2y+4, y+3 and 2y+4
Therefore ,
Perimeter of the shape = Sum of all the sides
= (3y+9) + (2y+4) + (y+3) + (2y+4)
= 3y + 2y + y + 2y + 9 + 4 + 3 + 4
= 8y + 20 (Ans)
2. Given,
Side of the square = 5x - 2
Therefore,
Perimeter of the square = 4 × Sides = 4s
= 4 × (5x - 2)
= 4 × 5x + 4 × (-2)
= 20x - 8 (Ans)
a patient needs of a low-dose pain reliever. the pharmacy sends pills marked . how many should be administered? round to the nearest tenth of a pill.
Answers
The pharmacy should send two pills marked for the patient to take.
To answer this question, we can use the formula below;
Dosage = (Amount of Drug x Patient's Weight) / Time
Since we don't have any information about the patient's weight or the time, we can't calculate the dosage.
However, we can calculate the number of pills required.
So, let's proceed with the calculation.
Each pill contains 2.5 mg of the pain reliever.
We need to administer a low dose, so let's assume the dose required is 5 mg.
To administer this dose, we need to give two pills, i.e., 2 x 2.5 = 5mg.
However, the question asks us to round the answer to the nearest tenth of a pill.
Since we can't divide a pill into parts, we need to round the answer up or down to the nearest whole pill.
In this case, since we need two pills, the answer is 2 pills.
For similar question on administer.
https://brainly.com/question/13152057
#SPJ11
In the basic EoQ model, if demand D-60 per month, stocking cost S-$12, and holding cost H-$10 per unit per month, what is the EOQ?
1.11
2.12
3.13
4.14
Answers
The EOQ in this case, is 12.
The optimal number of units to buy to satisfy demand while reducing inventory expenses including holding costs, shortage costs, and order costs is known as the economic order quantity (EOQ). Ford W. Harris created this production-scheduling concept in 1913, and it has since been improved. Demand, ordering, and holding costs are all taken into account in the economic order quantity calculation as constants.
The EOQ, or Economic Order Quantity, is the order quantity that minimizes the total inventory holding and ordering costs. To find the EOQ, we can use the formula:
EOQ = sqrt(2DS / H)
Plugging in the values given, we get:
EOQ = sqrt(2 * 60 * 12 / 10)
EOQ = sqrt(1440 / 10)
EOQ = sqrt(144)
EOQ = 12
So the EOQ, in this case, is 12.
To know more about EOQ visit :
brainly.com/question/13049890
#SPJ4
g(n)=n^2+2 find g(3)
how do i do this? i'll give brainliest and 10 pts
Answers
G(3) means substitute 3 into the equation n^2+2 so
3^2+2
9+2=11
Malcolm wants to make a deposit into an account that earns interest. He wants to be able to access the money on a limited basis. What type of account should he not consider?
a. Money market account
b. Statement savings account
c. Certificate of deposit
d. Savings account
Answers
The type of account he should not consider if he wants to access the money on a limited basis is; Choice D; Savings account.
What type of account should he not consider?It follows from the task content that Malcolm wants an account that earns interest and only wants to be able to access the money on a limited basis.
On this note, the account type which he should not consider is the savings account. This follows from the fact that, although savings account earns a relatively decent amount of interest, the owner is granted unlimited access to the money unlike in money market accounts and others.
Read more on savings account;
https://brainly.com/question/1287000
#SPJ1
Answer:
saving account
Step-by-step explanation:
I got it right
Please help me, I don't know

Answers
Answer:
3
4
5
Step-by-step explanation:
Henry left Terminal A 15 minutes earlier than Xavier, but reached Terminal B 30 minutes later than him. When Xavier reached Terminal B, Henry had completed & of his journey and was 30 km away from Terminal B. Calculate Xavier's average speed.
Answers
Xavier's average speed is 1 kilometer per minute.
To calculate Xavier's average speed, we need to determine the total time it took him to reach Terminal B and the distance traveled.
Given that Henry had completed 3/4 of the journey when Xavier reached Terminal B, it means Xavier took 1/4 of the total time for the journey. Since Xavier reached Terminal B 30 minutes earlier than Henry, we can infer that Xavier took 30 minutes for his part of the journey.
Since Henry was 30 km away from Terminal B when Xavier reached it, we can assume that Xavier traveled the remaining 30 km to reach Terminal B.
Therefore, Xavier's average speed can be calculated as the distance divided by the time:
Average Speed = Distance / Time = 30 km / 30 minutes = 1 km/minute.
For similar question on average speed.
https://brainly.com/question/4931057
#SPJ8
a bag contains 16 coins each with a different date. the number of possible combinations of three coins from the bag is
Answers
The number of possible combinations of three coins from the bag of 16 coins with different dates can be calculated using the formula for combinations, which is nCr = n! / r!(n-r)!, where n is the total number of objects, r is the number of objects to be chosen, and ! denotes factorial (the product of all positive integers up to the given number).
In this case, we have n = 16 (the total number of coins in the bag) and r = 3 (the number of coins to be chosen for each combination). Using the formula for combinations, we can calculate the number of possible combinations as follows:
nCr = 16! / 3!(16-3)!
nCr = (16 x 15 x 14) / (3 x 2 x 1)
nCr = 560
Therefore, 560 possible combinations of three coins can be chosen from the bag of 16 coins with different dates. These combinations could represent different historical events, significant dates, or other symbolic meanings depending on the dates inscribed on the coins. The calculation of combinations is an important concept in combinatorics and probability theory, and it has many real-world applications in fields such as statistics, economics, and computer science.
To learn more about Probability, visit:
https://brainly.com/question/13604758
#SPJ11
Find a Cartesian equation for the curve and identify it. r² cos(2θ) = 1 ellipse parabola circle hyperbola limaçon
Answers
The equation x² + y² = 1/cos²(θ) represents a circle centered at the origin with a radius of 1/cos(θ).
What is Cartesian equation?In a two-dimensional or three-dimensional plane, the cartesian form is useful for representing a point, a line, or a plane. The x, y, and z axes are correspondingly used to express the cartesian form with regard to the three-dimensional cartesian system.
To find a Cartesian equation for the curve described by the polar equation r²cos(2θ) = 1, we can use the conversion formulas:
x = r cos(θ)
y = r sin(θ)
Substituting these into the given equation, we have:
(x² + y²)cos(2θ) = 1
Expanding the cosine term using the double-angle formula, cos(2θ) = cos²(θ) - sin²(θ), we get:
(x² + y²)(cos²(θ) - sin²(θ)) = 1
Simplifying further, we have:
x²cos²(θ) + y²cos²(θ) - x²sin²(θ) - y²sin²(θ) = 1
Using the identity cos²(θ) + sin²(θ) = 1, we can substitute it in the equation:
x² + y² - x²sin²(θ) - y²sin²(θ) = 1
Rearranging terms, we obtain:
x²(1 - sin²(θ)) + y²(1 - sin²(θ)) = 1
Using the identity 1 - sin²(θ) = cos²(θ), we can simplify further:
x²cos²(θ) + y²cos²(θ) = 1
Finally, dividing both sides by cos²(θ), we get:
x² + y² = 1/cos²(θ)
The equation x² + y² = 1/cos²(θ) represents a circle centered at the origin with a radius of 1/cos(θ).
Learn more about Cartesian equation on:
https://brainly.com/question/30087444
#SPJ4
What is the value of x?

Answers
Answer:
46°
Step-by-step explanation:
from large triangle:
let the third unknown angle be 'a'
then,
a+x+7+85=180
a=88-x
now,from small triangle,
let the third unknown angle be 'b'
then,
b+x+2x=180
b=180-3x
b=a (vertically opposite angles)
then,
180-3x=88-x
2x=92
x=46
How do I solve (3.4) (6.7) using standard algorithm?
Answers
To solve the equation (3.4)(6.7) using the standard algorithm, first multiply 3.4 and 6.7. Then, the result is 22.78.
How to solve for the standard algorithm?The standard algorithm for multiplication is a step-by-step process that involves breaking down the numbers being multiplied into simpler parts, and then multiplying those parts together.
First, you would need to multiply the ones place of the first number (4) by the ones place of the second number (7), which would give you 28.
Next, you would need to multiply the ones place of the first number (4) by the tens place of the second number (6), which would give you 24.
Then, you would add the two products from steps 1 and 2 to get the result: 28 + 24 = 52.
Alternatively, you can use the distributive property of multiplication to simplify the problem.
(3.4)(6.7) = 3.46 + 3.40.7 = 22.8
Read more about standard algorithm here:
https://brainly.com/question/25232442
#SPJ1
an answering service staffed with one operator takes phone calls from patients for a clinic after hours. patient phone calls arrive at a rate of lambda equals 15 per hour. the interarrival time of the arrival process can be approximated with an exponential distribution. patient phone calls can be processed at a rate of mu equals 25 per hour. the processing time for the patient phone calls can also be approximated with an exponential distribution. determine the utilization factor.
Answers
The utilization factor can be calculated as the ratio of the arrival rate to the service rate. In this case, the arrival rate (lambda) is 15 per hour, and the service rate (mu) is 25 per hour. Therefore, it is important for the clinic to monitor the utilization factor and adjust staffing levels as needed to ensure efficient and effective patient communication.
So the utilization factor is:
Utilization factor = lambda / mu
Utilization factor = 15 / 25
Utilization factor = 0.6
This means that on average, the operator is utilized 60% of the time. In other words, there is a 40% idle time during which no phone calls are being processed. This is a relatively low utilization factor, which suggests that there is some capacity to handle more phone calls if necessary. However, it is important to note that if the arrival rate were to increase, the utilization factor would increase as well, which could lead to longer wait times for patients and potential bottlenecks in the phone system.
To know more about Exponential visit:
https://brainly.com/question/29631075
#SPJ11
(a) Find f(y|X=1/4).
(b) find E(Y|X=1/4).
(c) Find E(Var(Y|X) and Var(E(Y|X)).
(d) Find Var(Y).
Answers
The conditional probability density function of Y given X=1/4 is determined using the terms f(y|X=1/4), E(Y|X=1/4), E(Var(Y|X)), Var(E(Y|X)), and Var(Y). The marginal probability density function of Y is f(y) = ∫f(x,y)dx, and the expected value of the variance is E(Var(Y|X)) and Var(E(Y|X).
The given terms are f(y|X=1/4), E(Y|X=1/4), E(Var(Y|X) and Var(E(Y|X)), and Var(Y). Let's see what each term means:(a) f(y|X=1/4): It is the conditional probability density function of Y given X=1/4.(b) E(Y|X=1/4): It is the conditional expected value of Y given X=1/4.(c) E(Var(Y|X) and Var(E(Y|X)): E(Var(Y|X)) is the expected value of the variance of Y given X, and Var(E(Y|X)) is the variance of the expected value of Y given X.(d) Var(Y): It is the variance of Y.Step-by-step solution:(a) To find f(y|X=1/4),
we need to use the formula: f(y|x) = (f(x|y) * f(y)) / f(x)where f(y|x) is the conditional probability density function of Y given X=x, f(x|y) is the conditional probability density function of X given Y=y, f(y) is the marginal probability density function of Y, and f(x) is the marginal probability density function of X.Given that X and Y are jointly continuous random variables with joint probability density functionf(x,y) = 4xy, for 0 < x < 1 and 0 < y < 1and X ~ U(0,1), we have
f(x) = ∫f(x,y)dy
= ∫4xy dy
= 2x,
for 0 < x < 1
Using this, we can find the marginal probability density function of Y:f(y) = ∫f(x,y)dx = ∫4xy dx = 2y, for 0 < y < 1Now, we can find f(y|x):f(y|x) = (f(x,y) / f(x)) = (4xy / 2x) = 2y, for 0 < y < 1and 0 < x < 1Using this, we can find f(y|X=1/4):f(y|X=1/4) = 2y, for 0 < y < 1(b) To find E(Y|X=1/4), we need to use the formula:
E(Y|x) = ∫y f(y|x) dy
Given that X=1/4, we have
f(y|X=1/4) = 2y, for 0 < y < 1
Using this, we can find E(Y|X=1/4)
:E(Y|X=1/4) = ∫y f(y|X=1/4) dy
= ∫y (2y) dy= [2y^3/3] from 0 to 1= 2/3(c)
To find E(Var(Y|X)) and Var(E(Y|X)), we need to use the formulas:E(Var(Y|X)) = ∫Var(Y|X) f(x) dx
and Var(E(Y|X)) = E[(E(Y|X))^2] - [E(E(Y|X))]^2
Given that X ~ U(0,1), we havef(x) = 2x, for 0 < x < 1Using this, we can find
E(Var(Y|X)):E(Var(Y|X)) = ∫Var(Y|X) f(x) dx
= ∫[∫(y - E(Y|X))^2 f(y|x) dy] f(x) dx
= ∫[∫(y - x/2)^2 (2y) dy] (2x) dx
= ∫[2x(5/12 - x/4 + x^2/12)] dx
= [5x^2/18 - x^3/12 + x^4/48] from 0 to 1= 1/36
Using this, we can find Var(E(Y|X)):E(Y|X) = ∫y f(y|x) dy
= x/2andE[(E(Y|X))^2]
= ∫(E(Y|X))^2 f(x) dx
= ∫(x/2)^2 (2x) dx = x^4/8and[E(E(Y|X))]^2 =
[∫(E(Y|X)) f(x) dx]^2
= (∫(x/2) (2x) dx)^2
= (1/4)^2
= 1/16
Therefore, Var(E(Y|X)) = E[(E(Y|X))^2] - [E(E(Y|X))]^2
= (1/2) - (1/16)
= 7/16(d)
To find Var(Y), we need to use the formula: Var(Y) = E(Y^2) - [E(Y)]^2We have already found
E(Y|X=1/4):E(Y|X=1/4) = 2/3
Using this, we can find E(Y^2|X=1/4):
E(Y^2|X=1/4) = ∫y^2 f(y|X=1/4) dy
= ∫y^2 (2y) dy= [2y^4/4] from 0 to 1= 1/2Now, we can find Var(Y):
Var(Y) = E(Y^2) - [E(Y)]^2
= E[E(Y^2|X)] - [E(E(Y|X))]^2
= E[E(Y^2|X=1/4)] - [E(Y|X=1/4)]^2
= (1/2) - (2/3)^2
= 1/18
Therefore, the solutions are as follows:f(y|X=1/4) = 2y, for 0 < y < 1E(Y|X=1/4) = 2/3E(Var(Y|X)) = 1/36Var(E(Y|X)) = 7/16Var(Y) = 1/18.
To know more about probability density function Visit:
https://brainly.com/question/32512792
#SPJ11
let f(x,y,z)=xyz and |e={(x,y,z)∣0≤x≤1,x≤y≤1,y≤z≤x}. then which of the following represents a correct iterated integral of f(x,y,z)f(x,y,z) over ee?
Answers
The correct iterated integral of `f(x,y,z)` over `e` is:`int_{0}^{1} int_{x}^{1} int_{y}^{x} xyz dy dz dx`. The correct otpion is c.
Given that, `f(x,y,z)=xyz` and `e={(x,y,z) | 0≤x≤1, x≤y≤1, y≤z≤x}`.
To evaluate the iterated integral of `f(x,y,z)` over `e`, we need to set the limits of the iterated integral.
We have three variables, and we integrate the variable which is dependent on others first.
So, the correct iterated integral of `f(x,y,z)` over `e` is:`int_{0}^{1} int_{x}^{1} int_{y}^{x} xyz dy dz dx`
Therefore, option C represents a correct iterated integral of `f(x,y,z)` over `e`.
Option A is incorrect as it has the incorrect order of variables to be integrated, and the limits of the variables are also incorrect.
Option B is incorrect as the limits of the variable z are incorrect.
Option D is incorrect as it has the incorrect order of variables to be integrated.
The correct option is c.
Know more about the iterated integral
https://brainly.com/question/31067740
#SPJ11
Which of the following is the equation of a line that passes through the point(1.4) and is parallel to the x-axis?A. x = 4B. x = 1C. y = 4O D. y = 1
Answers
ANSWER
y = 4 (Option C)
EXPLANATION
We want to find the equation of the line that is parallel to the x axis and passes through point (1, 4)
First, it is important to note that all lines parallel to the x axis have gradient of zero (0).
Now, the equation of a line can generally br found by using:
\(y-y_1=m(x-x_1)\)where m = gradient/slope
x1, y1 = cordinates of the point that the line passes through.
Therefore:
\(\begin{gathered} x_1=\text{ 1} \\ y_1\text{ = 4} \end{gathered}\)Therefore, for the given line:
\(\begin{gathered} y\text{ - 4 = 0(x - 1)} \\ y\text{ - 4 = 0} \\ \Rightarrow\text{ y = 4} \end{gathered}\)That is the equation of the line.
Some tennis player's believe they have a better chance of winning the point if they are the one serving for the point. Suppose that in a particular match, Samson wins 46 of the 62 points when he's serving but only 23 of the 52 points when his opponent is serving. Does this data give convincing evidence that Samson plays better when serving? a) How much better did Samson perform when serving? Calculate the difference in the percentage of points won (the test statistic). Show work. b) State the hypotheses we are interested in testing. c) Suppose that the results of a simulation gave a p-value of 0.24, interpret this value. d) What conclusion would you make based on the p-value from part d? e) If your conclusion from part d was in error, what type of error did you commit? Explain. f) Describe this type of error in context. 9) Describe how to reduce the likelihood of this error occurring. h) If we concluded that Samson's ability to win points when serving is lower than his ability to win points when his opponent is serving, can we conclude that his serving is the cause of the difference?
Answers
(A) Total number of points served by Samson and multiply by 100 (B) Null hypothesis(H0) and Alternative hypothesis (Ha) (C) there would be a 24% chance of observing a difference in performance as extreme as the one observed in the data.
(D) Based on the p-value of 0.24, we do not have strong evidence to reject the null hypothesis. (E) it would be a Type II error. (F) Type II error would mean that we concluded there is no difference in Samson's performance when serving and when his opponent is serving, but in reality, there is a difference. (G) To reduce the likelihood of a Type II error occurring, we can increase the sample size (H) No, we cannot conclude that Samson's serving is the cause of the difference in his ability to win points when serving compared to when his opponent is serving
a) The difference in the percentage of points won when serving and when the opponent is serving can be calculated by subtracting the percentage of points won when the opponent is serving from the percentage of points won when serving. To find the percentage of points won when serving, we divide the number of points won when serving by the total number of points served by Samson and multiply by 100. Similarly, to find the percentage of points won when the opponent is serving, we divide the number of points won when the opponent is serving by the total number of points served by the opponent and multiply by 100.
b) The hypotheses we are interested in testing are:
- Null hypothesis (H0): There is no difference in Samson's performance when serving and when his opponent is serving.
- Alternative hypothesis (Ha): Samson performs better when serving compared to when his opponent is serving.
c) A p-value of 0.24 indicates that if the null hypothesis were true, there would be a 24% chance of observing a difference in performance as extreme as the one observed in the data. In other words, the p-value represents the probability of obtaining the observed difference in performance or a more extreme difference, assuming that there is no actual difference in Samson's performance when serving.
d) Based on the p-value of 0.24, we do not have strong evidence to reject the null hypothesis. This means that the data does not provide convincing evidence that Samson plays better when serving compared to when his opponent is serving.
e) If our conclusion from part d was in error, it would be a Type II error. This occurs when we fail to reject the null hypothesis even though it is false. In this case, it would mean that there is a difference in Samson's performance when serving, but we failed to detect it.
f) In the context of this question, a Type II error would mean that we concluded there is no difference in Samson's performance when serving and when his opponent is serving, but in reality, there is a difference. This could potentially lead to underestimating Samson's ability to perform better when serving.
g) To reduce the likelihood of a Type II error occurring, we can increase the sample size. By collecting more data, we can increase the power of our test and improve our ability to detect a difference in performance if it truly exists. Additionally, we can also adjust the significance level of our test (e.g., from 0.05 to 0.01) to make it more likely to detect smaller differences.
h) No, we cannot conclude that Samson's serving is the cause of the difference in his ability to win points when serving compared to when his opponent is serving. The data provided only shows an association between serving and winning points, but it does not establish a causal relationship. Other factors, such as skill, strategy, or the opponent's performance, could also contribute to the difference observed. To establish causality, further investigation and controlled experiments would be needed.
To know more about hypotheses refer to:
https://brainly.com/question/25263462
#SPJ11
John's son will start college in 10 years. John estimated a today's value of funds to finance college education of his son as $196,000. Assume that after-tax rate of return that John is able to earn from his investment is 8.65 percent compounded annually. He does not have this required amount now. Instead, he is going to invest equal amounts each year at the beginning of the year until his son starts college. Compute the annual beginning of-the-year payment that is necessary to fund the estimation of college costs. (Please use annual compounding, not simplifying average calculations).
Answers
John needs to make an annual beginning-of-the-year payment of approximately $369,238.68 to fund the estimated college costs of $196,000 in 10 years, given the after-tax rate of return of 8.65% compounded annually.
To compute the annual beginning-of-the-year payment necessary to fund the estimated college costs, we can use the present value of an annuity formula.
The present value of an annuity formula is given by:
P = A * [(1 - (1 + r)^(-n)) / r],
where P is the present value, A is the annual payment, r is the interest rate per period, and n is the number of periods.
In this case, John wants to accumulate $196,000 in 10 years, and the interest rate he can earn is 8.65% compounded annually. Therefore, we can substitute the given values into the formula and solve for A:
196,000 = A * [(1 - (1 + 0.0865)^(-10)) / 0.0865].
Simplifying the expression inside the brackets:
196,000 = A * (1 - 0.469091).
196,000 = A * 0.530909.
Dividing both sides by 0.530909:
A = 196,000 / 0.530909.
A ≈ 369,238.68.
Learn more about after-tax rate of return here:-
https://brainly.com/question/31825431?referrer=searchResults
#SPJ11
if y=24 when x=6, find y when x=-4.
Answers
Answer:
\(\huge\boxed{y=-16}\)
Step-by-step explanation:
We have to note that this represents a proportional relationship. This means that every time x increases by 1, y will increase by a proportional value.
In order to solve for proportions, we can create a proportion fraction which basically puts two variables over each other. Let's put x over y.
\(\frac{x}{y}\)
We know that in the first fraction, x=6 and y=24.
\(\frac{6}{24}\)
And we know that x=-4 but we have an unknown y value.
\(\frac{-4}{y}\)
We can now set these proportions equal to each other and solve for the missing y using cross products.
\(\frac{6}{24}=\frac{-4}{y}\) \(y = (24 \cdot -4) \div 6\) \(y = -96 \div 6\) \(y = -16\)Hope this helped!
consider the sample space given below. a die is a cube with six sides and each side contains one to six dots. suppose a blue die and a gray die are rolled together, and the numbers of dots that occur face up on each are recorded. the possible outcomes of the sample space s are listed as follows, where in each case the die on the left is blue and the one on the right is gray. s
Answers
The sample space provided represents the possible outcomes of rolling a blue die and a gray die together. Each die has six sides, numbered one to six. The sample space consists of 36 possible outcomes, which are the different combinations of numbers that can be rolled on both dice.
The first die has six possible outcomes (1, 2, 3, 4, 5, and 6), and for each outcome of the first die, there are six possible outcomes for the second die. Therefore, the sample space consists of 6 × 6 = 36 possible outcomes. Each outcome is represented by a pair of numbers, where the first number represents the number on the blue die and the second number represents the number on the gray die.
The sample space is an important concept in probability theory as it represents all the possible outcomes of an experiment. In this case, the experiment is rolling two dice together, and the sample space provides a complete list of all the possible outcomes. This can be used to calculate probabilities for different events, such as the probability of rolling a certain combination of numbers or the probability of rolling a certain sum of numbers. The sample space is also useful for visualizing the different outcomes and understanding the structure of the experiment.
Learn more about Sample space:
brainly.com/question/30206035
#SPJ11
Part of the population of 6,750 elk at a wildlife preserve is infected with a parasite. A random sample of 50 elk shows that 9 of them are infected. How many elk are likely to be infected?
Answers
When the sample is given, the number of elk are likely to be infected is to be considered as the 1,215.
Calculation of the number of elk:Since the population is 6,750.
The random sample is 50.
So here be like
\(6750\) ÷ \(50\) × \(9\)
= 1,215
hence, When the sample is given, the number of elk are likely to be infected is to be considered as the 1,215.
Learn more about sample here: https://brainly.com/question/24292263
DE is the perpendicular bisector of AC.
PLEASE HELP WILL GIVE BRAINLIEST!

Answers
Step-by-step explanation:
AB=BC
8x+6=6x+18
2x=12
x=6
so
AB= 48+6=54cm
BC=36+18=54cm
AD=CD
8y+20=12y-8
-4y=-28
y=7
so
AD= 84-8=76cm
CD=56+20=76cm
AE=2x+4y
AE=2×6+4×7
AE=40cm
AC=2×40=80cm
If an 8-foot ladder is placed 3 feet from the wall, what is the approximate height it will reach on the wall?
11 feet
7 feet
5 feet
Answers
Answer:
5 feet
Step-by-step explanation:
because 8-3 is 5 hope this helps
-2/4 + 6/8=
and: 1.8 - (3.7) =
(Both different math problems)
(Please do the full math!! don’t just show answer)
Answers
-2/4 + 6/8 and 1.8 - (3.7) is simplified to give 1/ 4 and -1. 9 respectively.
How to solve the equationsGiven the equations as;
-2/4 + 6/81.8 - (3.7)With the knowledge of BODMAS, we have
a. -2/4 + 6/8
Find the LCM
= -4 + 6/ 8
Add the numerators
= 2/ 8
Find the common division
= 1/ 4
b. 1.8 - (3.7)
Expand the bracket
1. 8 - 3. 7
Find the difference
= -1. 9
Thus, -2/4 + 6/8 and 1.8 - (3.7) is simplified to give 1/ 4 and -1. 9 respectively.
Learn more about BODMAS here:
https://brainly.com/question/723406
#SPJ1
Help me with this pls ASAP

Answers
Answer:
90 degrees counterclockwise or 270 degrees clockwise
Step-by-step explanation:
Hope this helps
A line passes through the points (1,-6) and (4,3) What is the Y intercept of this line?

Answers
Answer: b=-9
Step-by-step explanation:
To find the y-intercept of the line, we can use the points given to make an equation. To find the slope, you use the formula \(m=\frac{y_2-y_1}{x_2-x_1}\).
\(m=\frac{3-(-6)}{4-1} =\frac{9}{3} =3\)
Now that we know the slope, we can fill in what we know and solve for y-intercept.
y=3x+b
We can plug in any point to solve for y-intercept.
3=3(4)+b [multiply]
3=12+b [subtract both sides by 12]
b=-9
Now, we know that the y-intercept is b=-9.
Help!A 2-column table with 5 rows. Column 1 is labeled Type of flower with entries lilies, daisies, carnations, asters, daffodils. Column 2 is labeled Amount with entries 60, 36, 72, 42, 24.
The florist makes the greatest number of identical arrangements with the lilies and the daisies. Which combination describes the arrangements?
A.6 arrangements with 10 lilies and 6 daisies
B.6 arrangements with 6 lilies and 10 daisies
C.12 arrangements with 10 lilies and 6 daisies
D.12 arrangements with 5 lilies and 3 daisies
Answers
The greatest number of identical arrangements the florist can make is .12 arrangements with 5 lilies and 3 daisies.
What is the greatest number of identical arrangements?The greatest number of identical arrangements with the lilies and the daisies the florist can make would be equivalent to the highest common factor of the number of lilies and daisies.
The highest common factor of two or more numbers is the highest number that can divide the numbers evenly without leaving any remainder. For example, the highest common factor of 4 and 8 is 4.
Factors of 60= 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Common factors = 1, 2, 3, 4, 6, 12
Highest common factor = 12
Number of daisies = 36 /12 = 3
Number of lilies = 60 / 12 = 5
To learn more about highest common factor, please check: https://brainly.com/question/26073850
#SPJ1
The length of cell A is
3×10−5
m. The length of cell B is
0.000001
m. What is the ratio of cell A's length to cell B's length?
Answers
Answer:
b´s length is 10
Step-by-step explanation:
sorry to be a bug again but please help with 8, 9, and 10 please!

Answers
8) The percent of people that said that Pinocchio was their favorite Disney Movie is of: 28%.
9) The percent of people that said that Pinocchio or Cars was their favorite Disney movie is of: 39%.
10) The two movies that about half the people say were their favorite is of: Pinocchio and Toy Story.
How to obtain the percentages?From the pizza graph, the sum of all the percentages must be of 100%, hence the Pinocchio percentage is obtained as follows:
10 + 11 + 14 + 15 + 22 + P = 100
72 + P = 100
P = 100 - 72
P = 28%.
Then the percentage for Pinocchio or Cars is of:
28 + 11 = 39%.
The percentage for Pinocchio or Toy Story is of:
28 + 22 = 50%.
(about half).
More can be learned about percentages at https://brainly.com/question/24877689
#SPJ1