Differentiate implicitly to find the first partial derivatives of z. 11x2 + 2y^2 + 5z^2 = 4 ϑz/ϑx =
ϑz/ϑy =
Answers
The first partial derivatives of z are:
∂z/∂x = -22x / (10z)
∂z/∂y = -4y / (10z)
To find the first partial derivatives of z with respect to x and y in equation 11x^2 + 2y^2 + 5z^2 = 4, we will differentiate the equation implicitly with respect to x and y.
First, let's find ∂z/∂x:
Differentiate both sides of the equation with respect to x:
22x + 0 + 10z(∂z/∂x) = 0
Now, solve for ∂z/∂x:
10z(∂z/∂x) = -22x
∂z/∂x = -22x / (10z)
Next, let's find ∂z/∂y:
Differentiate both sides of the equation with respect to y:
0 + 4y + 10z(∂z/∂y) = 0
Now, solve for ∂z/∂y:
10z(∂z/∂y) = -4y
∂z/∂y = -4y / (10z)
So, the first partial derivatives of z are:
∂z/∂x = -22x / (10z)
∂z/∂y = -4y / (10z)
Learn more about the first partial derivatives: https://brainly.com/question/30217886
#SPJ11
Related Questions
3. Find the equations of the lines that form the sides to the polygon shown below. What type of polygon is it? Explain your reasoning.
Answers
Answer: The question is not complete. the figure is attached below.
The polygon is a rectangle.
Step-by-step explanation:
Line 1 goes through (-2, 3)
hence the slope of line 1 = -3/2
Line 2 goes through (0, 3) (2, 0)
hence the slope of line 2 = -3/2
Line 3 goes through (0, 1) (-3, 1)
hence the slope of line 3 = 2/3
Line 4 goes through (3, 0) (0, -2)
Hence the slope of line 4 = 2/3
therefore -3/2 * 2/3 = -1
Line1 + Line3 Line1 + Line4 Line2 + Line3 Line2+Line4
because, the distance between Line1 and Line2 is not equal to that Line3 and Line4.
The polygon is a rectangle polygon.

Which equation demonstrates the associative property of multiplication?

Answers
Answer:
A
Step-by-step explanation:
The parentheses are switched around, making the answer still the same. However, for Answer choice C, it is Commutative Property because the factors are switched around.
=====================================================
Explanation:
The equation shown for choice A is in the form p*(q*r) = (p*q)*r which is the general format for the associative property of multiplication.
In this case, p = 2.5, q = 1/5 and r = 2/3.
The order of p,q,r stays the same while the parenthesis shift around. The stuff in the parenthesis is done first before anything else. Though with multiplication, the order doesn't matter which is why we can freely shift the parenthesis like this.
Addition has a similar rule which says p+(q+r) = (p+q)+r.
can i please get the answers for this? i’ve been trying to find it for half an hour

Answers
Answer:
What's the full question? I'm not sure how to help with just this information :(
Solve the differential equation y" 4y' 12y = 0.
Answers
The solution to the given differential equation is "y(t) = c1 e^(-2t) cos(2t√2) + c2 e^(-2t) sin(2t√2)".
To solve the differential equation y'' + 4y' + 12y = 0, we first find the characteristic equation by assuming that the solution is of the form y = e^(rt), where r is a constant:
r^2 e^(rt) + 4r e^(rt) + 12 e^(rt) = 0
Dividing both sides by e^(rt) gives:
r^2 + 4r + 12 = 0
We can solve for r using the quadratic formula:
r = [-4 ± sqrt(4^2 - 4(1)(12))] / (2(1))
r = [-4 ± sqrt(16 - 48)] / 2
r = [-4 ± sqrt(-32)] / 2
r = -2 ± 2i√2
So, the general solution to the differential equation is:
y(t) = c1 e^(-2t) cos(2t√2) + c2 e^(-2t) sin(2t√2)
where c1 and c2 are constants determined by initial conditions.
Therefore, the solution to the differential equation y'' + 4y' + 12y = 0 is:
y(t) = c1 e^(-2t) cos(2t√2) + c2 e^(-2t) sin(2t√2).
You can learn more about differential equation at
https://brainly.com/question/1164377
#SPJ11
Solve b + 3∕8 = 4∕9 for b.
Question options:
A)
5∕72
B)
59∕72
C)
1∕6
D)
32∕27
Answers
Answer:
5/72
Step-by-step explanation:
Simplify 3t-4u + 8t- u
Answers
Answer:
11t-5u
Step-by-step explanation:
combine like terms
3t-4u+8t-u
(3t+8t)+(-4u-u)
(11t)+(-5u)
11t-5u
Hopes this helps please mark brainliest
Answer:
11t - 5u
Step-by-step explanation:
Given expression,
→ 3t - 4u + 8t - u
Let's solve the given expression,
→ 3t - 4u + 8t - u
→ (3t + 8t) + (-4u - u)
→ 11t - 5u
Hence, the answer is 11t - 5u.
The following are rules for repeating patterns. For which rule will the 12th shape be a circle?
A. Triangle, Circle,Square
B. Circle, Square
C. Rectangle,Circle
Circle, Circle, Triangle
Answers
The third pattern because you can divide 12 by the number of shapes in the sequence and start counting from the remainder.
In this case choice C has 5 shapes. 12/5 is 2, with a remainder of 2.
The second term in choice C is Circle, so choice C is the answer.
Of course, you can also list them all out.
If there is no remainder when you divide then the 12th term is the last term in the sequence.
Answer:
yes
Step-by-step explanation:
what is 25,00+30,00=
Answers
Answer:
5,500
Step-by-step explanation:
2,500 + 3,000:
2000 + 3000 + 500
5000 + 500
5500
Easy!
Using separation of variables, solve the differential equation,
e^−y (sec(x))−dydxcos(x)=0.
Answers
Therefore, the solution to the given differential equation is: y = -cos(x)(x + C), where C is the constant of integration.
To solve the differential equation using separation of variables, we will separate the variables and integrate.
e^(-y) sec(x) - dy/dx cos(x) = 0
Rearranging the equation:
e^(-y) sec(x) = dy/dx cos(x)
Divide both sides by e^(-y) sec(x) to isolate the variables:
dy/dx = cos(x) / (e^(-y) sec(x))
Now, we can separate the variables by multiplying both sides by dx:
dy / (cos(x) e^(-y)) = dx
Next, integrate both sides with respect to their respective variables:
∫ dy / (cos(x) e^(-y)) = ∫ dx
The integral of the left side can be simplified using substitution. Let u = e^(-y), then du = -e^(-y) dy:
∫ -du / (cos(x) u) = ∫ dx
Applying the integral:
ln|u| / cos(x) = x + C
Substituting back u = e^(-y):
ln|e^(-y)| / cos(x) = x + C
Using the property ln(e^a) = a, we have:
(-y) / cos(x) = x + C
Simplifying further:
y = -cos(x)(x + C)
To know more about differential equation,
https://brainly.com/question/31767641
#SPJ11
Sarah used 3.25 meters of fabric to make a costume. How many centimeters of fabric did she use?
Answers
Answer:
325 centimeters
Step-by-step explanation:
Find the MEAN, MODE, MEDIAN, and RANGE for the following Data: 6, 8,4, 1,4,7

Answers
Answer:
Mean:5
Mode: 4
Range: 7
Median: 5
Step-by-step explanation:
Please help me!!!!!!!!

Answers
We can see here that the solutions to the triangles are:
1. 62.2°.
2. 35.9°
3. 61.9°
4. 53.1°
How we arrived at the solutions?We can see here that using trigonometric ratio formula, we find the values of x.
We see the following:
1. Cos x = 7/15 = 0.4666
x = \(cos^{-1}\) 0.4666 = 62.2°.
2. Sin x = 27/46 = 0.5869
x° = \(sin^{-1}\) 0.5869 = 35.9°
3. Sin x = 30/34 = 0.8823
x° = \(sin^{-1}\) 0.8823 = 61.9°
4. Tan x = 8/6 = 1.3333
x° = 1.3333 = 53.1°
Learn more about triangle on https://brainly.com/question/1058720
#SPJ1
what is the range of the function y = 2sin x?
Answers
The range of the function y = 2sin(x) is the set of all possible values that the function can take. The range of the function y = 2sin(x) is [-2, 2].
In trigonometry, the sine function can be defined as the ratio of the length of the opposite side to that of the hypotenuse in a right-angled triangle. The sine function, sin(x), has a range between -1 and 1, inclusive. When we multiply the sine function by 2, as in the case of y = 2sin(x), the range is expanded.
Multiplying the range of sin(x) [-1, 1] by 2 gives us the range of 2sin(x), which is [-2, 2].
Therefore, the range of the function y = 2sin(x) is [-2, 2].
Learn more about function here:
https://brainly.com/question/28468393
#SPJ11
Classify the polynomial by degree and number of terms
v4 - 3v² +5v + 10
Answers
if x2 y2 z2 = 9, dx dt = 8, and dy dt = 9, find dz dt when (x, y, z) = (2, 2, 1).
Answers
Using implicit differentiation dz/dt = -34
What is differentiation?Differentiation is the process of finding the derivative of a function.
Since x² + y² + z² = 9, dx/dt = 8, and dy/dt = 9, we need to find dz/dt when (x, y, z) = (2, 2, 1).
So, differentiating implicitly and also applying the chain rule, we have that
x² + y² + z² = 9
d(x² + y² + z²)/dt = d9/dt
dx²/dx × dx/dt + dy²/dy × dy/dt + dz²/dz × dz/dt = d9/dt
2xdx/dt + 2ydy/dt + 2zdz/dt = 0
xdx/dt + ydy/dt + zdz/dt = 0
Making dz/dt subject of the formula, we have that
zdz/dt = -(xdx/dt + ydy/dt)
dz/dt = -(xdx/dt + ydy/dt)/z
Given that
dx/dt = 8, dy/dt = 9, x = 2, y = 2 and z = 1Substituting the values of the variables into the equation, we have that
dz/dt = -(xdx/dt + ydy/dt)/z
dz/dt = -(2 × 8 + 2 × 9)/1
= -(16 + 18)/1
= - 34
So, dz/dt = -34
Learn more about implicit differentiation here:
https://brainly.com/question/29543075
#SPJ1
The question is incomplete. Here is the complete question
If x² + y² + z² = 9, dx/dt = 5, and dy/dt = 4, find dz/dt when (x, y, z) = (2, 2, 1).
I need help ASAP!!!Only people that know the answer is right thanks

Answers
Answer:
700mi cube
Step-by-step explanation:
10x7x10=700mi cube
What initial investment must be made to accumulate $120000 in 12 years if the money is invested in a mutual fund that pays 14%annual interest, compounded monthly? Use the analytical solution to find the answer.
Answers
What initial investment must be made to accumulate $120000 in 12 years if the money is invested in a mutual fund that pays 14%
annual interest, compounded monthly?
Remember that
The compound interest formula is equal to
\(A=P(1+\frac{r}{n})^{nt}\)where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have
A=$120,000
t=12 years
r=14%=14/100=0.14
n=12
substitute in the given formula
\(120,000=P(1+\frac{0.14}{12})^{12\cdot12}\)Solve for P
P=$22,583.425. What linear function defines the following Arithmetic Sequence?
-4, -1, 2, 5, 8,...
an = 4 - 3(n-1)
an = -4 -3(n-1)
an = 4 + 3(n - 1)
an = -4 + 3(n - 1)

Answers
Answer
A
Step-by-step explanation:
The linear function defines the arithmetic sequence is an = -4 + 3(n - 1). The correct option is D.
What is an arithmetic progression?
The sequence in which every next number is the addition of the constant quantity in the series is termed the arithmetic progression.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
The given series is -4, -1, 2, 5, 8. The common difference of the series is calculated as,
d = -1 - ( -4 )
d = -1 + 4
d = 3
The equation will be written as,
an = a₁ + d(n - 1)
an = -4 + 3(n - 1)
Therefore, the linear function that defines the arithmetic sequence is an = -4 + 3(n - 1). The correct option is D.
To know more about arithmetic progression follow
https://brainly.com/question/6561461
#SPJ2
Question Four Consider the following production function: y = f(z)=z¼/^z/2. Assuming that the price of the output is p and the prices of inputs are w, and w₂ respectively: (a) State the firm's profit maximization problem. (2 marks). (b) Derive the firm's factor demand functions for z; and zo. (10 marks). (c) Derive the firm's supply function. (5 marks). = 2. (d) Derive the firm's profit function. (3 marks). an (e) Verify Hotelling's lemma for q(w, p), z₁(w, p) and z₂(w, p). (6 marks). az (f) State the firm's cost minimization problem. (2 marks), (g) Derive the firm's conditional factor demand functions. (8 marks). (h) Derive the firm's cost function. (4 marks). Cond: 69 Porat funct
Answers
The text discusses a production function and addresses various aspects of a firm's decision-making. It covers profit maximization, factor demand functions, supply function, profit function, Hotelling's lemma, cost minimization, conditional factor demand functions, and the cost function. These concepts are derived using mathematical calculations and formulas. Hotelling's lemma is verified, and the cost function is determined.
(a) The firm's profit maximization problem can be stated as follows: Maximize profits (π) by choosing the optimal levels of inputs (z and zo) that maximize the output (y) given the prices of output (p) and inputs (w, w₂).
(b) To derive the firm's factor demand functions, we need to find the conditions that maximize profits.
The first-order condition for input z is given by:
∂π/∂z = p * (∂f/∂z) - w = 0
Substituting the production function f(z) = z^(1/4) / z^(1/2) into the above equation, we have:
p * (1/4 * z^(-3/4) / z^(1/2)) - w = 0
Simplifying, we get:
p * (1/4 * z^(-7/4)) - w = 0
Solving for z, we find:
z = (4w/p)^(4/7)
Similarly, for input zo, the first-order condition is:
∂π/∂zo = p * (∂f/∂zo) - w₂ = 0
Substituting the production function f(zo) = z^(1/4) / z^(1/2) into the above equation, we have:
p * (1/2 * z^(1/4) * zo^(-3/2)) - w₂ = 0
Simplifying, we get:
p * (1/2 * z^(1/4) * zo^(-3/2)) - w₂ = 0
Solving for zo, we find:
zo = (2w₂ / (pz^(1/4)))^(2/3)
(c) To derive the firm's supply function, we need to find the level of output (y) that maximizes profits.
Using the production function f(z), we can express y as a function of z:
y = z^(1/4) / z^(1/2)
Given the factor demand functions for z and zo, we can substitute them into the production function to obtain the supply function for y:
y = (4w/p)^(4/7)^(1/4) / (4w/p)^(4/7)^(1/2)
Simplifying, we get:
y = (4w/p)^(1/7)
(d) The firm's profit function is given by:
π = p * y - w * z - w₂ * zo
Substituting the expressions for y, z, and zo derived earlier, we have:
π = p * ((4w/p)^(1/7)) - w * ((4w/p)^(4/7)) - w₂ * ((2w₂ / (pz^(1/4)))^(2/3))
(e) To verify Hotelling's lemma, we need to calculate the partial derivatives of the profit function with respect to the prices of output (p), input z (z₁), and input zo (z₂).
Hotelling's lemma states that the partial derivatives of the profit function with respect to the prices are equal to the respective factor demands:
∂π/∂p = y - z * (∂y/∂z) - zo * (∂y/∂zo) = 0
∂π/∂z₁ = -w + p * (∂y/∂z₁) = 0
∂π/∂z₂ = -w₂ + p * (∂y/∂z₂) = 0
By calculating these partial derivatives and equating them to zero, we can verify Hotelling's lemma.
(f) The firm's cost minimization problem can be stated as follows: Minimize the cost of production (C) given the level of output (y), prices of inputs (w, w₂), and factor demand functions for inputs (z, zo).
(g) To derive the firm's conditional factor demand functions, we need to find the conditions that minimize costs. We can express the cost function as follows:
C = w * z + w₂ * zo
Taking the derivative of the cost function with respect to z and setting it to zero, we get:
∂C/∂z = w - p * (∂y/∂z) = 0
Simplifying, we have:
w = p * (1/4 * z^(-3/4) / z^(1/2))
Solving for z, we find the conditional factor demand for z.
Similarly, taking the derivative of the cost function with respect to zo and setting it to zero, we get:
∂C/∂zo = w₂ - p * (∂y/∂zo) = 0
Simplifying, we have:
w₂ = p * (1/2 * z^(1/4) * zo^(-3/2))
Solving for zo, we find the conditional factor demand for zo.
(h) The firm's cost function is given by:
C = w * z + w₂ * zo
Substituting the expressions for z and zo derived earlier, we have:
C = w * ((4w/p)^(4/7)) + w₂ * ((2w₂ / (pz^(1/4)))^(2/3))
This represents the firm's cost function.
To know more about profit maximization problem, refer here:
https://brainly.com/question/29787532#
#SPJ11
The number of pounds of dog food that a pet store has is represented by the equation y = negative 15 x + 430, where x represents the number of days that the store is open and y represents the pounds of dog food in stock in the store. How many pounds of dog food will the pet store have after 21 days? 92 115 315 336
Answers
Answer: B) 115 pounds
Step-by-step explanation:
Because x is the number of days passed, after 21 days, x = 21.
\(y = -15(21)+430\\\\Multiply\\\\y = -315+430\\\\y=115\)
Hope it helps <3
Answer:
115
Step-by-step explanation:
got it correct on edge 2020
A rock sample containing an isotope with a half-life of 28 million years has an initial mass of 184 grams. how much time has elapsed after three half-lives?
Answers
The half life period is the time in which only half of the given population remains. It can be represented through this equation:
\(f(t)=a\times(1/2)^{\frac{t}{h}}\)
t = time passeda = y-intercepth = half lifeSolving the QuestionWe're given:
h = 28 million yearsa = 184 grams (this is the initial mass, after 0 time has passed)For most questions like this, we would have to plug these values into the equation mentioned above. However, this question asks for the time elapsed after 3 half-lives.
This can be calculated simply by multiplying the given half-life by 3:
28 million years x 3
= 84 million years
Answer84 million years
Which congruence statement is correct?
A. △DMQ ≅ △SRB
B. △MDQ ≅ △RBS
C. △QDM ≅ △SRB
D. △MQD ≅ △SBR
Answers
Based on the AAS conrguence theorem, the congruence statement that is correct is: B. △MDQ ≅ △RBS.
What is the AAS Congruence Theorem?According to the AAS conrguence theorem, when two consecutive angles and a non-included side of a triangle is congruent to the corresponding two consecutive angles and a non-included side of another triangle, both triangles are said to be congruent triangles.
The two pairs of consecutive congruent angles are: ∠M ≅ ∠R; and ∠D ≅ ∠B
The one pair of non-included congruent sides is: MQ ≅ RS
Therefore, the correct congruence statement is: B. △MDQ ≅ △RBS.
Learn more about the AAS congruence theorem on:
https://brainly.com/question/385
#SPJ1

Factor x2 – 3x – 28. An x-method chart shows the product a c at the top of x and b at the bottom of x. Above the chart is the expression a x squared + b x + c. Identify the values that should be written to complete the X diagram. On the top: On the bottom: On the sides: Rewrite the expression using the numbers on the sides of the X diagram. Use double grouping to factor the four terms. x2 – 3x – 28 =
Answers
Answer:
(x - 7)(x + 4)
Step-by-step explanation:
Note that 4 times 7 is 28, and that -7x + 4x = -3x.
Therefore, x^2 - 3x - 28 factors into (x - 7)(x + 4)
The factors of the quadratic equation x² – 3x – 28 is (x - 7)(x + 4).
What is a quadratic equation?
It is a polynomial with a degree of 2 or the maximum power of the variable is 2 in quadratic equations. It has two solutions as its maximum power is 2.
Writing a number or any mathematical object as the result of several factors—typically smaller or simpler objects of the same kind—is known as factorization or factoring in mathematics.
The factorization will be done as below:-
x² – 3x – 28
Split the middle term as 7 and 4.
x² – 7x + 4x – 28 = 0
x ( x - 7 ) + 4 ( x -7 ) = 0
Take x-7 common from the whole equation.
( x - 7 ) ( x + 4 ) = 0
Therefore, the factors of the quadratic equation x² – 3x – 28 is (x - 7)(x + 4).
To know more about quadratic equations follow
https://brainly.com/question/1214333
#SPJ2
Compare the investment below to an investment of the same principal at the same rate compounded annually.
principal: $9,000, annual interest: 9%, interest periods: 12, number of years: 20
After 20 years, the investment compounded periodically will be worth:
(Round to two decimal places as needed.)
more than the investment compounded annually.

Answers
After 20 years, the investment compounded periodically will be worth $ 3, 238. 47 more than the investment compounded annually.
How to find the investment value ?First, find the value of the investment when it is compounded periodically, 12 times a year.
The formula is:
= Amount invested x ( 1 + rate ) ^ number of periods
= 9, 000 x ( 1 + 9 % / 12 ) ^ ¹² ˣ ²⁰
= $ 53, 678. 16
If compounded annually, the value would be :
= 9, 000 x ( 1 + 9 % ) ²⁰
= $ 50, 439. 69
The difference is :
= 53, 678. 16 - 50, 439. 69
= $ 3, 238. 47
Find out more on investments at https://brainly.com/question/15201573
#SPJ1
can someone help me with this asap.
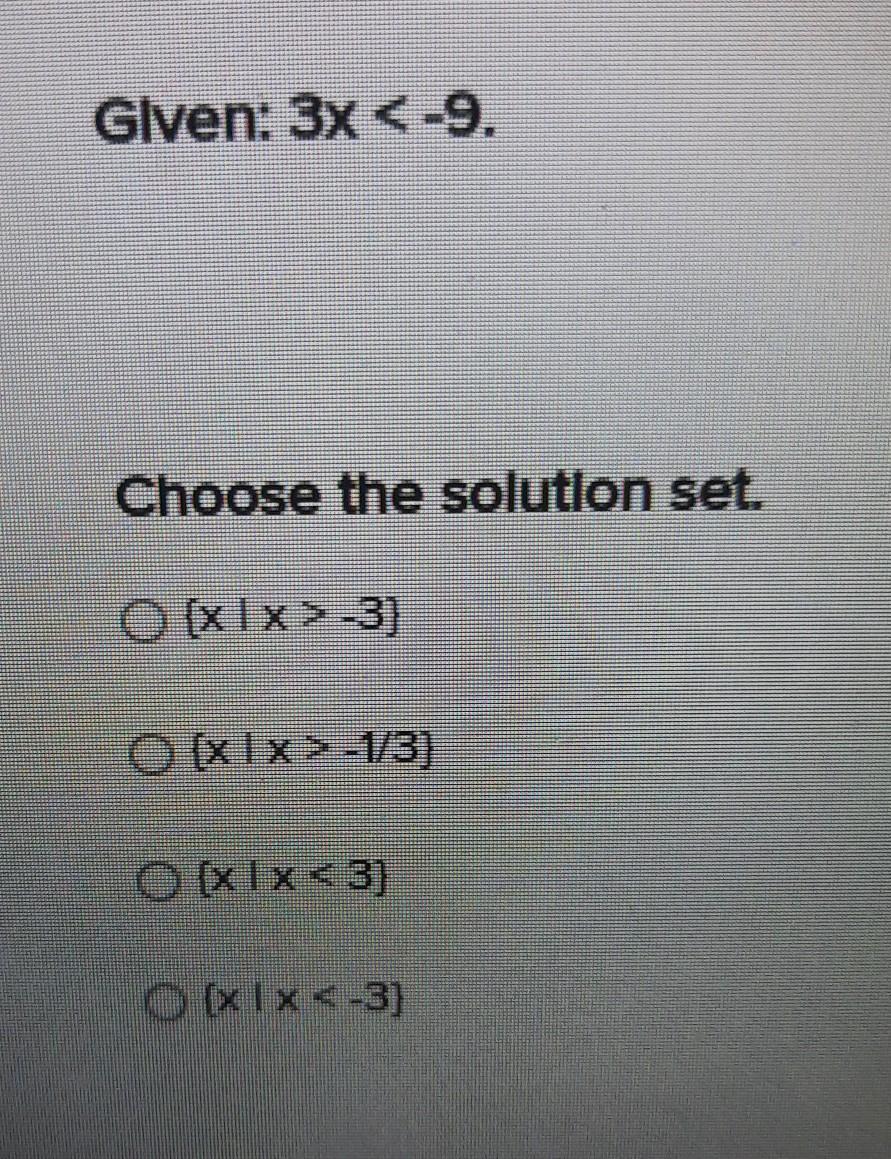
Answers
Answer:
fourth option
Step-by-step explanation:
Given
3x < - 9 ( divide both sides by 3 )
x < - 3
solution set is { x | x < - 3 }
Consider the sum 10 + 21 +32 +43 + ... +406. A. How many terms (summands) are in the sum? B. Compute the sum using a technique discussed in this section.
Answers
A. There are 37 terms in the sum.
B. The sum of the given series is 7,696.
How many terms are in the sum?A. Using arithmetic sequences, We can observe that each term in the sum is obtained by adding 11 to the previous term. Therefore, the nth term can be expressed as:
\(a_n = 10 + 11(n-1)\)
We want to find the number of terms in the sum up to \(a_n\) = 406. Setting \(a_n\)= 406 and solving for n, we get:
406 = 10 + 11(n-1)
396 = 11(n-1)
n = 37
Therefore, there are 37 terms in the sum.
How to compute the sum?B. We can use the formula for the sum of an arithmetic series:
\(S_n = n/2 * (a_1 + a_n)\)
where \(S_n\) is the sum of the first n terms, \(a_1\) is the first term, and\(a_n\) is the nth term.
In this case, we have:
\(a_1\)= 10
\(a_n\)= 406
n = 37
Substituting these values, we get:
\(S_{37}\) = 37/2 * (10 + 406)
\(S_{37}\) = 18.5 * 416
\(S_{37}\) = 7,696
Therefore, the sum of the given series is 7,696.
Learn more about arithmetic sequences
brainly.com/question/15412619
#SPJ11
What do Kiera's actions in chapter 2 reveal?
A) She believes in her mother and deals with her problems on her own to su
B) She feels uncomfortable at the luncheon, but she shows up to support her
C) She doubts her mother will win the election, but she supports her anyway
D) She knows things are changing at her house; however, she seeks friends
Answers
Kiera's actions reveal a combination of options A, B, and D. Firstly, Kiera demonstrates her belief in her mother's abilities by taking charge and handling a problematic situation independently.
When her mother's campaign video fails to load, Kiera promptly steps in and manages to get the content loaded, exhibiting her resourcefulness and support for her mother's cause. Furthermore, Kiera attends the luncheon despite feeling uneasy and out of place, indicating her willingness to show up and support her mother's endeavors. However, Kiera's discomfort highlights her struggles with her mother's newfound political fame, and the changes that come with it, such as the exclusive event that she attends. Lastly, Kiera's decision to seek out friends and social connections suggests her recognition of the shifting dynamics in her household and her need for companionship amidst the family's political spotlight. Therefore, Kiera's actions in chapter 2 reveal her loyalty and support for her mother's campaign, but also her internal conflict and search for stability amidst the changes in her life.
Learn more about Kiera's actions here :
https://brainly.com/question/31014501
#SPJ11
What is the unit rate per year?

Answers
Answer:
3.6
Step-by-step explanation:
divide 36 by 10 be sure it's the easiest part
Answer:
Unit rate per year is :---
\( \frac{(50.4 - 7.2)}{(14 - 2)} = \frac{43.2}{12} = \boxed{3.6 \: feet \: per \: year} \\\)
3.6 feet per year is the right answer.An independent set in a graph is a set of vertices S⊆V that contains no edge (so no pair of neighboring vertices is included). The max independent set problem is to find an independent set of maximum size in a graph G. (a) Write the max independent set problem as an integer linear program. (b) Write an LP relaxation for the max independent set problem. (c) Construct an example (a family of graphs) to show that the ratio LP-OPT / OPT can be at least cn where c>0 is some absolute constant and n is the number of vertices of the graph. (d) What is the (exact) relation between the size of a max independent set and the size of min vertex cover of a graph? (e) Using this relation, what does the 2-approximation algorithm for vertex cover imply for an approximation algorithm for max independent set?
Answers
The independent set in a graph is a set of vertices that contain no edges. So, no neighboring vertices are included. The max independent set problem is to get an independent set of maximum size in graph G.
The solution for this question is discussed below:
a) The integer linear program for the max independent set problem is as follows:
maximize ∑x_i Subject to: x_i+x_j ≤ 1 {i,j} ∈ E;x_i ∈ {0, 1} ∀i. The variable x_i can represent whether the ith vertex is in the independent set. It can take on two values, either 0 or 1.
b) The LP relaxation for the max independent set problem is as follows:
Maximize ∑x_iSubject to:
xi+xj ≤ 1 ∀ {i, j} ∈ E;xi ≥ 0 ∀i. The variable xi can take on fractional values in the LP relaxation.
c) The family of graphs is as follows:
Consider a family of graphs G = (V, E) defined as follows. The vertex set V has n = 2^k vertices, where k is a positive integer. The set of edges E is defined as {uv:u, v ∈ {0, 1}^k and u≠v and u, v differ in precisely one coordinate}. It can be shown that the size of the max independent set is n/2. Using LP, the value can be determined. LP provides a value of approximately n/4. Therefore, the ratio LP-OPT/OPT is at least c/4. Therefore, the ratio is in for a constant c>0.
d) The size of a max-independent set is equivalent to the number of vertices minus the minimum vertex cover size.
e) The 2-approximation algorithm for vertex cover implies a 2-approximation algorithm for the max independent set.
To know more about the independent set, visit:
brainly.com/question/31418821
#SPJ11
The heights of two similar cylinders are 3cm and 4cm respectively. The total area of the bigger cylinder is 400cm².Calculate the total surface area of the smaller cyl
Answers
Answer:
Step-by-step explanation:
Total surface area = 2πr(r+h)
If the total area of the bigger cylinder is 400cm² and radius is 4cm, then;
400=2(3.14)(r)(r+4)
400= 6.26r(r+4)
400=100.48 + 25.12h
299.52 = 25.12h
H = 299.52/25.12
H = 11.92cm
For the smaller cylinder
The height is calculated as;
H/h = R/r
11/92/