determine weather it is no solution many solutions or one solutions
3(6-4m)=2(9-6m)
Answers
Answer:
Many solutions
Step-by-step explanation:
Related Questions
- ii: word problems - use the 3-step process to solve each word problem! the larger number is 18 more than twice the smaller. if the sum of the two numbers is 93, find both numbers.
Answers
The smaller number is 25, and the larger number is 68. The larger number is 18 more than twice the smaller number, and their sum is 93.
To solve this word problem using the 3-step process, we need to find the two numbers given that the larger number is 18 more than twice the smaller and the sum of the two numbers is 93.
Step 1: Let's assign variables to the unknown numbers. Let's say the smaller number is "x" and the larger number is "y".
Step 2: Translate the given information into equations. From the problem, we know that the larger number is 18 more than twice the smaller. So, we can write the equation as: y = 2x + 18.
We also know that the sum of the two numbers is 93. So, we can write another equation as: x + y = 93.
Step 3: Solve the system of equations. We have two equations:
y = 2x + 18
x + y = 93
We can solve this system of equations by substitution method or elimination method. Let's use substitution.
Substitute the value of y from the first equation into the second equation:
x + (2x + 18) = 93
3x + 18 = 93
3x = 93 - 18
3x = 75
x = 75 / 3
x = 25
Now, substitute the value of x back into the first equation to find y:
y = 2(25) + 18
y = 50 + 18
y = 68
So, the smaller number is 25 and the larger number is 68.
To learn more about substitution method visit:
https://brainly.com/question/22340165
#SPJ11
Which equations have 8 as a solution?
15-n=7 n + 3 = 12 4n = 32
64 : n = 8
Select all the equations that have 8 as a solution.
A. 15-n=7
B. n + 3 = 12
C. 4n = 32
D. 64:n = 8
Answers
Answers:
15 - n = 7
-15 -15
-n = -8
n = 8
4n = 32
n = 8
Select all the equations that have 8 as a solution.
Answers:
A and C
Explanation is above.
Hope this helps!
Answer:
The equations 15 - n = 7, 4n = 32, and 64 : n = 8 have 8 as a solution.
Step-by-step explanation:
Each equation will have work shown below :
15 - n = 7
For this equation, we would need to isolate the variables by doing the inverse operation to both sides of the equation. Here in this equation, the operation is to subtract and the inverse operation of that is addition. Since the original operation is subtraction, we need to add it by a negative sign to each side. In order to isolate the variables, we have to add -7 to both sides.
15 - n = 7
+ -7 + -7
8 = n
The right side has a sum of 0 so it doesn't require any value to the equation. As you can see in the equation, n equals to 8.
4n = 32
For this equation, we would need to isolate the variables by doing the inverse operation to both sides of the equation. Here in this equation, the operation is to multiply and the inverse operation of that is division. In order to isolate the variables, we have to divide 8 to both sides.
4n = 32
/4 /4
n = 8
The left side has a quotient of 0 so it doesn't require any value to the equation. As you can see in the equation, n equals to 8.
This is a ratio which is basically just the operation of division. For this equation, we would need to isolate the variables by doing the inverse operation to both sides of the equation. Here in this equation, the operation is to divide and the inverse operation of that is multiplication. Since the original operation is division, we need to multiply it by the reciprocal to each side. In order to isolate the variables, we have to multiply 1/8 to both sides.
64 : n = 8
* 1/8 * 1/8
8 = n
The right side has a product of 0 so it doesn't require any value to the equation. As you can see in the equation, n equals to 8.
Consider this polynomial, where a is an unknown real number.
p(t) = x^4 +5x^3 + ax^2 - 3x + 11
The remainder of the quotient of P(x), and (x+ 1) is 17.
Braulio uses synthetic division to find the value of a, and Zahra uses the remainder theorem to find the value of a.

Answers
Answer:
Brauilo is wrong because he divided by (x+1) instead of (x-1)
Step-by-step explanation:
The remainder Theorem states that
if polynomial f(x) is divided by binomial x-a, the remainder will equal f(a). The factor is positive so the binomial is the same as
which is why we divide by -1, or subsitue -1 into the equation p(x).
The remainder of a polynomial division can be gotten using remainder theorem or synthetic division.
The true statement is: Brauilo did not find the value of a, because he divided by (x+1) instead of (x-1)
From the question, we have the following parameters:
\(\mathbf{p(x) = x^4 +5x^3 + ax^2 - 3x + 11}\)
\(\mathbf{Divisor =x+ 1}\)
\(\mathbf{Remainder = 17}\)
First, we set the divisor to 0.
\(\mathbf{Divisor =x+ 1 = 0}\)
So, we have:
\(\mathbf{x+ 1 = 0}\)
Solve for x
\(\mathbf{x= -1}\)
The above equation means that, the value of x that will be used to test the polynomial is -1
From the question,
Zahra used \(\mathbf{x= -1}\); this is represented as: P(-1)Braulio used \(\mathbf{x= 1}\); this is represented in the synthetic divisionHence, Braulio is incorrect, because he used the wrong value of x
Read more about polynomial division at:
https://brainly.com/question/12011809
What is the measure of ZSPQ in the figure below?
10
P
S
28°
10
R
Q
A. 14°
B. 62°
OC. 56°
D. 28°
E. 15°
F. Cannot be determined

Answers
The measure of angle SPQ is 56°
What is trigonometric ratio?the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths.
Sin(θ) = opp/hyp
cosθ = adj/hyp
tanθ = opp/adj
To calculate the hypotenuse , we have known the adjascent to angle 28°.
Therefore;
cos 28 = 10/x
0.883 = 10/x
x = 10/0.883
x = 11.3
Represent angle SPR by y
cos x = 10/11.3
cos x = 0.883
x = 28°
Therefore the measure of angle SPQ is 28+28 = 56°
learn more about trigonometric ratio from
https://brainly.com/question/24349828
#SPJ1
Help pls I will give Brianlist

Answers
Answer:
A
Step-by-step explanation:
Hope this helps :)
Answer:
A
Step-by-step explanation:
8. Solve the system of equations shown by substitution.
y = x - 5 5x + 2y = 4
F. (10,5)
G. (-1,-6)
H. (0,-5)
J. (2,-3)
Answers
Answer:
J. (2, -3)
Step-by-step explanation:
1. Substitute y = x - 5 in for y in the other equation:
5x + 2(x - 5) = 4
2. Simplify:
5x + 2x - 10 = 4 (distributed the 2)
7x - 10 = 4
3. Isolate for x:
7x - 10+10 = 4+10
7x = 14
7x/7 = 14/7
x = 2
4. Plug the new x value into an equation and solve for y:
y = 2 - 5
y = -3
hope this helps!
I do not really understand how to get to the answer?

Answers
Given the information on the table, we can see the following increases on the minimum wage:
From 1980 to 1981 : 0.25
1981 to 1990: 0.45
1990 to 1996: 0.95
1996 to 1997: 0.4
1997 to 2007: 0.7
2007 to 2009:1.4
As we can see, the minimum wage has a tendency to grow with the passing of the years, but there is not a constant of growth. Therefore, we could use the mean of these increments, and use it to estimate the approximate minimum wage for 2020. First we get the mean of this 6 numbers:
\(\mu=\frac{0.25+0.45+0.95+0.4+0.7+1.4}{6}=\frac{4.15}{6}=0.691\)We have that, in average, the minimum wage increased 0.691 from 1981 to 2009, then, an approximation for the current year would be the following:
\(\begin{gathered} 2009\rightarrow7.25 \\ 2010\rightarrow7.94 \\ 2011\rightarrow8.63 \\ 2012\rightarrow9.32 \\ 2013\rightarrow10.01 \\ 2014\rightarrow10.70 \\ 2015\rightarrow11.39 \\ 2016\rightarrow12.08 \\ 2017\rightarrow12.72 \\ 2018\rightarrow13.46 \\ 2019\rightarrow14.15 \\ 2020\rightarrow14.84 \end{gathered}\)then, the minimum wage for the current year should be $14.84, because the mean of the increments of the given data would give us an approximate of $14.84
PLS DO NUMBER 7 WILL MARK BRAINLY AND ALSO GIVE AN ADDITIONAL 100 PTS IF CORRECT PLS HURRY. THANK YOU

Answers
Answer: f(x)=-3x+2
Step-by-step explanation:

A watch company is developing packaging for its new watch. The designer uses octagons with a base area of 30 in2 and rectangles with a length of 10 in to create a prototype for the new package. What is the volume of the prototype?
140 in3
200 in3
240 in3
300 in3
Answers
Answer: 300 in3
Step-by-step explanation: To find the volume you multiply the base area by the height. 30 x 10 = 300. Did this for my exam and got the question correct.
The volume of the prototype is 300in^3.
Calculation of the volume of the prototype:Since The designer uses octagons with a base area of 30 in2 and rectangles with a length of 10 in to create a prototype for the new package.
So here the volume is
= 30(10)
= 300
Therefore, The volume of the prototype is 300in^3.
Learn more about volume here: https://brainly.com/question/17481620
Suppose you have an algorithm A that takes as input an array M[0,1,...,n - 1] of n integers. The algorithm is defined by two functionsf: Z → Zand g: ZXZ â€" Z. If n = 1, then the algorithm computes a function f (g), where is the single entry in the array, and returns this integer value. For larger values of n, the algorithm Computes two new arrays that start at positions i = 0 and [n/3 - 1] and that include [2n/3] elements. Thus, if n = 15, the new arrays would begin at positions 0 and 4 and contain 10 elements each The algorithm then runs recursively on each subarray, and stores the value. This returns an ordered set of two integers, x, y,. The algorithm then computes g(x, y), and returns this value. We would like to write down a function (n) for the running time of this algorithm on inputs of arrays of n elements. Assume that computing f (9) and g(x, y) each cost only one operation. Counting all the operations for each step, which of the following recurrence relations would seem to fit? To make the problem easy to solve, you should assume that n = 3k for some non-negative integer a. t(1) = and t(n) = 2t(n/2) + 1, for some positive constant C O b. t(1) = C, and t(n) = 21(2n/3), for some positive constant c. 1(1) = C, and t(n) = 2t(2n/3) + C2, for some positive constants C, C2 d. 1(1) = C, and t(n) = 21(2n/3) + C2n, for some positive constants C, C2 e. f(1) = C, and t(n) = 2t(n/3) + C2, for some positive constants C, C2
Answers
Based on the given algorithm, we can analyze the recurrence relation for the running time of the algorithm on inputs of arrays of n elements.
Let's denote the running time of the algorithm for an input of size n as t(n).
For n = 1, the algorithm computes f(g) for a single entry in the array, which costs a constant time, let's say C1. Therefore, we have:
t (1) = C1
For larger values of n, the algorithm splits the array into two subarrays of size 2n/3 each and runs recursively on each subarray. This step incurs a running time of t(2n/3) for each subarray.
Additionally, the algorithm performs the computation g(x, y) on the resulting ordered set of two integers, which costs a constant time, let's say C2.
Considering these factors, we can write the recurrence relation for the running time as:
t(n) = 2t(2n/3) + C2
Therefore, the correct option among the given recurrence relations that seems to fit the running time of the algorithm is:
c. t(1) = C, and t(n) = 2t(2n/3) + C2, for some positive constants C, C2
Learn more about recurrence relation here:
brainly.com/question/27381972
#SPJ11
for any integer n5, can there be a simple graph that has n vertices all of different degrees? why?
Answers
No, it is not possible to have a simple graph with n vertices, where n is any integer greater than or equal to 5, such that all vertices have different degrees.
In a simple graph, the degree of a vertex refers to the number of edges connected to that vertex. The maximum degree possible in a graph with n vertices is (n-1), which occurs when one vertex is connected to all other vertices.
To create a graph where all vertices have different degrees, we would need to assign a unique degree to each vertex. However, if n is greater than or equal to 5, we cannot assign n unique degrees to n vertices while satisfying the conditions of a simple graph.
To see why, consider the case of n = 5. We need to assign degrees 1, 2, 3, 4, and 5 to the vertices.
The vertex with degree 5 must be connected to all other vertices, leaving us with four remaining degrees (1, 2, 3, and 4) to assign to the remaining four vertices. However, no matter how we distribute these degrees, at least two vertices will have the same degree.
This argument can be extended to any value of n greater than 5. Therefore, it is not possible to construct a simple graph with n vertices where all vertices have different degrees for any integer n ≥ 5.
To know more about simple graph refer here:
https://brainly.com/question/33247524#
#SPJ11
8 is what percent of 128?
Answers
Answer:
10.24
Step-by-step explanation:
128 x .08= 10.24
(the 8 in the equation is moved 2 places to the left because its a percentage)
In the given problem of percentage, 8 is 6.25\(\%\) of 128.
Percentage is a way of expressing a proportion or a relative value as a fraction of 100. It represents a portion or a fraction of a whole in terms of hundredths.
The term "percentage" comes from the Latin word "per centum," which means "per hundred."
The percentage is denoted using the symbol "\(\%\)". For example, 25\(\%\) means 25 out of 100, or 25 hundredths.
When working with percentages, it is often used to compare or represent ratios, proportions, or relative quantities. It provides a convenient way to express fractions or ratios in a standardized form.
Percentages are commonly used in various fields, such as finance, economics, statistics, and everyday situations involving ratios, discounts, interest rates, statistics, and probability. They provide a standardized way to express relative values and make comparisons across different quantities.
\(\frac{8}{128} \times 100\) = \(\frac{25}{4}\)\(\%\)
= 6.25\(\%\).
So, the percentage of 8 out of 128 is 6.25\(\%\).
Learn more about percentages here:
https://brainly.com/question/16797504
#SPJ6
PLEASEEEE HELP LE OUT!!!
The steps a student preformed to solve the equation 7h - ( 3h - 5) = 2(h - 7 ) are shown below. Explain each step the student preformed to solve the equation

Answers
Answer:
\({ \sf{7h - (3h - 5) = 2(h - 7)}} \\ \\ { \sf{7h - 3h + 5 = 2h - 14}}\)
[distributive property open brackets ]
\({ \sf{4h + 5 = 2h - 14}}\)
[simplification of either sides]
\({ \sf{4h - 2h = - 14 - 5}}\)
[operating similar terms]
\({ \sf{2h = - 19}} \\ \)
[simplification]
\({ \sf{h = \frac{ - 19}{2} }}\)
Which situation could be represented by the equation 38.25 = 3x?
A group of 3 friends each had $38.25. What is x, the total amount of money the friends had all together?
A group of friends had $38.25. They decided to triple their money by working for a neighbor. What is x, the total amount of money the friends had all together after working for a neighbor?
A group of 3 friends had $38.25 all together. Each friend had the same amount of money. What is x, the amount of money each friend had?
A group of friends had $38.25. They earned $3 more. What is x, the amount of money the friends have all together?
Answers
Answer:
A
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
10. Find the width of the canyon.
13.
width = ?
22 m
15 m
160 m
I need help asap

Answers
Answer:
Therefore, the width of the canyon is 109.09 meters.
Step-by-step explanation:
* 160/22 = k (Scale Factor)
7.2727 = k
* Let x be the width of the canyon
x / 15 = k
x / 15 = 7.2727
x = 7.2727 (15)
x = 109.09 m
The width of the canyon is 109.09m.
The calculation is as follows:Here we assume x be the width of the canyon.
The k(Scale factor) should be
= \(160 \div 22\)
k = 7.2727
So,
\(x \div 15 = k\\\\ x \div 15 = 7.2727\)
x = 109.09 m
Learn more: brainly.com/question/17429689
A tree is 28.05 feet tall. What is its height in meters? Use the following conversion: 1 meter is 3.3 feet.
Answers
Answer:
It is 8.5 meters tall
Step-by-step explanation:
28.05 / 3.3 = 8.5
Write an equation for the line (line touches (0,-3) and (5,8))

Answers
The equation is [y = (11/5)x - 3] for the line touches (0, -3) and (5, 8).
Define the term line?In a graph, a line is a straight curve that connects two or more points. It is used to represent relationships between two variables, such as x and y.
To write an equation for the line passing through the points (0,-3) and (5,8), we can use the point-slope form of the equation of a line, which is:
y - y₁ = m(x - x₁)
where m is the slope of the line, and (x₁, y₁) is one of the given points on the line. The slope:
m = (y₂ - y₁) / (x₂ - x₁)
where (x₁, y₁) and (x₂, y₂) are the two given points on the line.
Using the points (0, -3) and (5, 8), we can find the slope:
m = (8 - (-3)) / (5 - 0) = 11/5
Now we can use the point-slope form of the equation of the line, with (0,-3) as the given point:
y - (-3) = (11/5) (x - 0)
Simplifying this equation, we get:
y + 3 = (11/5) x
Subtracting 3 from both sides, we get the final equation for the line:
y = (11/5)x - 3
To know more about line segment, visit:
https://brainly.com/question/280216
#SPJ1
Create one equation 3(x+3)= x +
Answers
Answer: 4 (x +3) - 3+9=x
Step-by-step explanation:
Please help 100 points

Answers
Answer:
vertex: (-5, -6)p-value: -1opens downwardStep-by-step explanation:
You want the vertex and p-value for a parabola with focus (-5, -7) and directrix y = -5.
VertexThe vertex of a parabola is halfway between the focus and directrix. That is because every point on the parabola is the same distance from the focus as from the directrix.
When the vertex is above or below the directrix, it will have the same x-value as the focus. Its y-value will be the average of those of the focus and directrix:
The vertex is ...
(h, k) = (-5, (-7-5)/2)
(h, k) = (-5, -6) . . . . vertex
P-valueThe p-value for the parabola is half the distance from the focus to the directrix. When the focus is below the directrix, the p-value is negative.
p = (-7 -(-5))/2 = -1
This is equivalent to the distance from the focus to the vertex.
p = (-7 -(-6)) = -1 . . . . p-value
The sign of the p-value tells you the direction the parabola opens. For negative p-values, the parabola opens downward.
The p-value shows up in the equation for the parabola this way:
\(y=\dfrac{1}{4p}(x-h)^2+k\qquad\text{vertex at $(h,k)$}\)
__
Additional comment
We don't know what your drop-down menu of choices says about the parabola. We have guessed that it might refer to the direction the parabola opens. It always opens in the direction toward the focus and away from the directrix.
<95141404393>

what is the probability of rolling two numbers that sum to 4 after two rolls of the six-sided die (the sum of the two numbers from each roll equals 6)?
Answers
The probability of rolling two numbers that sum to 4 after two rolls of a six-sided die is 1/9 or approximately 0.1111. This means that out of all possible combinations, there is a 1 in 9 chance of obtaining a sum of 4.
To calculate the probability, we need to consider all possible outcomes of two dice rolls and determine the favorable outcomes where the sum of the two numbers equals 4.
Let's analyze the possible combinations for the first roll:
1 + 3 = 4
2 + 2 = 4
3 + 1 = 4
Out of these three combinations, only one of them results in a sum of 4.
For the second roll, we have the same possible combinations as the first roll. Again, only one combination gives a sum of 4.
Since the rolls are independent events, we can multiply the probabilities of each roll to find the probability of both events occurring. Therefore, the probability of rolling two numbers that sum to 4 is:
(1/6) * (1/6) = 1/36
However, we rolled the dice twice, so we need to account for the order in which these combinations can occur. We have two favorable outcomes: (1 + 3) and (3 + 1). Therefore, the probability becomes:
2 * (1/36) = 1/18
However, there are two possible ways to achieve a sum of 4: (1 + 3) and (3 + 1). Thus, we need to multiply by 2 again:
2 * (1/18) = 1/9
To know more about probability, visit
https://brainly.com/question/13604758
#SPJ11
Please help giving brainlist
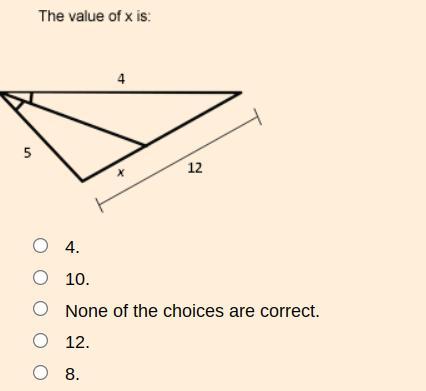
Answers
Answer:
None of the choices are correct.
Step-by-step explanation:
The angles are marked to show they are equal, therefore the line segment that divides the angle into two equal parts is an angle bisector.
Angle Bisector Theorem
The angle bisector of any angle will divide the opposite side in the ratio of the sides containing the angle.
\(\implies \sf \dfrac{5}{4}=\dfrac{x}{12-x}\)
\(\implies \sf5(12-x)=4x\)
\(\implies \sf 60-5x=4x\)
\(\implies \sf 9x=60\)
\(\implies \sf x=\dfrac{60}{9}\)
\(\sf \implies x=\dfrac{20}{3}\)
\(\\ \rm\Rrightarrow \dfrac{4}{5}=\dfrac{12-x}{x}\)
\(\\ \rm\Rrightarrow 4x=5(12-x)\)
\(\\ \rm\Rrightarrow 4x=60-5x\)
\(\\ \rm\Rrightarrow 9x=60\)
\(\\ \rm\Rrightarrow x=6.67\)
Option C none of the above
An investor wants to invest 30000 in corporate bonds that are rated AAA, A, and B. The lower rated ones pay higher interest, but pose a higher risk as well. The average yield is 5% on AAA bonds, 6% on A bonds, and 10% on B bonds. Being conservative, the investor wants to have twice as much in AAA bonds as in B bonds. How much should she invest in each type of bond to have an interest income of 2000?
Answers
The investor should invest $5000 in AAA bonds, $2500 in B bonds, and the remaining $22500 in A bonds to have an interest income of $2000.
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity.
Let x be the amount invested in AAA bonds.
Since the investor wants to have twice as much in AAA bonds as in B bonds, the amount invested in B bonds is x/2.
The remaining amount invested in A bonds is 30000 - x - x/2 = 30000 - 3x/2.
The interest income from AAA bonds is 0.05x.
The interest income from A bonds is 0.06(30000 - 3x/2) = 1800 - 0.09x.
The interest income from B bonds is 0.1(x/2) = 0.05x.
The total interest income is the sum of the interest income from each type of bond, which is given to be $2000.
0.05x + 1800 - 0.09x + 0.05x = 2000
Simplifying and solving for x, we get:
-0.04x + 1800 = 2000
-0.04x = 200
x = 5000
Hence, the investor should invest $5000 in AAA bonds, $2500 in B bonds, and the remaining $22500 in A bonds to have an interest income of $2000.
To learn more on Percentage click:
https://brainly.com/question/28269290
#SPJ1
Bertie has 3494 comic books he wants them in groups of 8 how many comics would be left over after putting them in groups of 8
Answers
Answer: 6 would be left
Step-by-step explanation: divide 3494 by 8
There will be 6 comics left over after putting them in groups of 8
What is a unitary method?A unitary method is a mathematical way of obtaining the value of a single unit and then deriving any no. of given units by multiplying it with the single unit.
Given, Bertie has 3494 comic books he wants them in groups of 8.
∴ The no. of groups can be obtained if we divide the total number of books by no. of books in each group which is,
= (3494/8).
= 438×8 + 6.
So, There will be 6 comics left over after putting them in groups of 8.
learn more about the unitary method here :
https://brainly.com/question/28276953
#SPJ2
Macy made a 220 grooming dogs one day in her mobile grooming business she charges 60 per appointment and 40 earned in tips write an equation to represent the situation and solve the equation to determine how many appointments Messi had part B Logan made a profit of 300 as a mobile groomer he charge $70 per appointment and received $50 in tips but he had to pay a rental fee for the truck of $20 per appointment write an equation to represent the situation and solve the situation to determine how many appointments Logan had

Answers
Macy had 3 appointments.
Logan had 5 appointments.
What is the quadratic equation?
A quadratic equation is a type of polynomial equation of degree 2, which is written in the form of "ax^2 + bx + c = 0", where x is the variable and a, b, and c are constants. The solutions to a quadratic equation can be found using the quadratic formula: x = (-b ± √(b^2 - 4ac))/2a.
Part A:
Let x be the number of appointments Macy had.
We know that the total income (60x + 40) must equal 220.
Therefore, the equation representing the situation is:
60x + 40 = 220
To solve for x, we can subtract 40 from both sides:
60x = 180
Finally, we divide both sides by 60 to get:
x = 3
Macy had 3 appointments.
Part B:
Let y be the number of appointments Logan had.
We know that the total profit (70y + 50 - 20y) must equal 300.
Therefore, the equation representing the situation is:
50y + 50 = 300
To solve for y, we can subtract 50 from both sides:
50y = 250
Finally, we divide both sides by 50 to get:
y = 5
Logan had 5 appointments.
To learn more about quadratic equations, Visit
https://brainly.com/question/1214333
#SPJ1
what is the answer for this one 4x + 16 = ?
Answers
Answer:
4(x+4)
Step-by-step explanation:
Factor 4x+16
4x+16
=4(x+4)
Explanation: 4x + 16 = 24
4x + 16-16 = 24 -16
4x=8
4x/4=8/4
x=2
You are shopping for single-use cameras to hand out at a party. The daylight cameras cost $2.75 and the flash cameras cost$4.25. You must buy exactly 20 cameras and you want to spend between $65 and$75, inclusive. Write and solve a compound inequality for this situation. Then list all the solutions that involve whole numbers of cameras.
Answers
The compound inequality for the given situation is $2.75x + $4.25y ≥ $65 and $2.75x + $4.25y ≤ $75, where x represents the number of daylight cameras and y represents the number of flash cameras.
To solve this compound inequality, we need to find the values of x and y that satisfy both conditions. The inequality $2.75x + $4.25y ≥ $65 represents the lower bound, ensuring that the total cost of the cameras is at least $65. The inequality $2.75x + $4.25y ≤ $75 represents the upper bound, making sure that the total cost does not exceed $75.
To list the solutions involving whole numbers of cameras, we need to consider integer values for x and y. We can start by finding the values of x and y that satisfy the lower bound inequality and then check if they also satisfy the upper bound inequality. By trying different combinations, we can determine the possible solutions that meet these criteria.
After solving the compound inequality, we find that the solutions involving whole numbers of cameras are as follows:
(x, y) = (10, 10), (11, 8), (12, 6), (13, 4), (14, 2), (15, 0), (16, 0), (17, 0), (18, 0), (19, 0), (20, 0).
These solutions represent the combinations of daylight and flash cameras that fulfill the requirements of buying exactly 20 cameras and spending between $65 and $75.
Learn more about compound inequality
brainly.com/question/17957246
#SPJ11
solve the system of inequalities:

Answers
x<4
5x-1>6-2x
get all the terms on the same side
7x>7
divide by 7
x>1
x-5<0
add 5 to both sides
x<5
When placed end to end, 5 yellow lego bricks are 2 cm longer than 2 green lego bricks. While 3 green lego bricks are 2 cm longer than 7 yellow lego bricks. How long are 5 green lego bricks?
Answers
Answer:
5 green lego bricks are equal to 12 yellow lego bricks
Step-by-step explanation:
Let the yellow and green lego bricks be denoted by y and g respectively.
According to the given conditions
5y+ 2= 2g------ equation 1
3g+2= 7y----- equation 2
Rearranging the equations and adding
5y+ 2= 2g------ equation 3
7y-2= 3g----- equation 4
12y= 5g
5 green lego bricks are equal to 12 yellow lego bricks
Mr. Hernandez bakes specialty cakes. He uses many different containers of various sizes and shapes to
bake the parts of his cakes. Select all of the following containers which hold the same amount of batter
Need Help ASAP!

Answers
Answer:
The answer is A and B
The volume of a sphere with radius r is given by the formula V = (4/3)πr^3. The volume of a hemisphere with radius r is given by the formula V = (2/3)πr^3.
If we substitute r = 2 cm in the formulas, we get:
- Volume of sphere = (4/3)π(2)^3 = (4/3)π(8) = 32/3π
- Volume of hemisphere = (2/3)π(2)^3 = (2/3)π(8) = 16/3π
So, the sphere with a radius of 2 cm and the hemisphere with a radius of 5 cm have the same volume of 32/3π cubic centimeters.
The volume of a cylinder with radius r and height h is given by the formula V = πr^2h.
If we substitute r = 10 cm and h = 7 cm in the formula, we get:
- Volume of cylinder = π(10)^2(7) = 700π cubic centimeters
The volume of a cone with radius r and height h is given by the formula V = (1/3)πr^2h.
If we substitute r = 4 cm and h = 2 cm in the formula, we get:
- Volume of cone = (1/3)π(4)^2(2) = 32/3π cubic centimeters.
Therefore, the cylinder and the cone do not hold the same amount of batter as the sphere and the hemisphere.
Can somebody please answer this quickly

Answers
Answer:
0.115
Step-by-step explanation: