determine the product of the two polynomials using the distributive property (3x-1)(2x^2+5x-8)
Answers
6x^3+13x^2-29x+8
Let me know if you need a show of work!
Related Questions
A car salesperson had $79,327 in total monthly sales in July and $88,798 in August. The salesperson earned $2,890 in commission from those combined sales. What is the salesperson's commission as a percent of their total sales for the two months? Enter your answer, rounded to the nearest tenth of a percent, in the box. %
Answers
Total sales for the two months - July and August = 79,327 + 88798 = $168,125
The salesperson's commission in percentage =
\(\frac{2890}{168125}\times100\text{ = 17.187}\approx17.2\text{ \%}\)HELP!!!
Which point is located at (-5,5)?
point K
point L
point F
point G

Answers
Answer:
The correct answer is point F!
Step-by-step explanation:
Hope it helped :D
Answer:
point f
Step-by-step explanation:
-5 in x and 5 and y
ANSWER: POINT F
Solve for x: (5 points)
E)
(-4/3)x-6=-26
A:27
B:-27
C:15
D:-15
Answers
(-4/3)x=20
x = 15
3/8 to the 2nd power
Answers
Answer:
9/64
Step-by-step explanation:
it is just 3/8 x 3/8
Which has a greater effect on the volume-changing the radius by a given amount or changing the height by the same amount? Why?
Answers
Answer: Changing the radius of an object by a given amount has a greater effect on the volume than changing the height by the same amount. The volume of a cylinder is given by the formula V = πr²h, where V is the volume, r is the radius, and h is the height. If we change the radius by a given amount, say x, the new radius would be r+x. Hence, the new volume would be V' = π(r+x)²h = π(r²+2rx+x²)h = V + 2πrxh + πx²h. We can see that the volume change equals 2πrxh + πx²h. The first term is proportional to both the radius and the height, whereas the second term is proportional to the square of the radius and the height. Assuming that the height change is also x, the new volume would be V'' = πr²(h+x) = V + πr²x. We can see that the volume change is proportional to the radius squared and the change in height. Therefore, changing the radius by a given amount has a greater effect on the volume than changing the height by the same amount.
Find the Center and Radius (x-9)^2+(y+4)^2=36
Answers
Answer:
The center is (9, -4), and the radius is
√36 = 6.
what is the perimeter of a square that has an area of 25 square feet?
Answers
We know that the perimeter of a squate is (Where x is the side of the square):
\(P=4x\)and we know that the area is:
\(A=x^2\)So we can repace the area to find x so:
\(\begin{gathered} 25=x^2 \\ x=\sqrt[]{25}=5 \end{gathered}\)So the perimeter will be:
\(P=4\cdot5=20\)So the perimeter is 20 feet
Given A (-10,-3.5) and B (2, 5.5), find the coordinates of point P on AB so that P partitions AB in the ratio 5:1.
Answers
\(\textit{internal division of a line segment using ratios} \\\\\\ A(-10,-3.5)\qquad B(2,5.5)\qquad \qquad \stackrel{\textit{ratio from A to B}}{5:1} \\\\\\ \cfrac{A\underline{P}}{\underline{P} B} = \cfrac{5}{1}\implies \cfrac{A}{B} = \cfrac{5}{1}\implies 1A=5B\implies 1(-10,-3.5)=5(2,5.5)\)
\((\stackrel{x}{-10}~~,~~ \stackrel{y}{-3.5})=(\stackrel{x}{10}~~,~~ \stackrel{y}{27.5})\implies P=\underset{\textit{sum of the ratios}}{\left( \cfrac{\stackrel{\textit{sum of x's}}{-10+10}}{5+1}~~,~~\cfrac{\stackrel{\textit{sum of y's}}{-3.5+27.5}}{5+1} \right)} \\\\\\ P=\left( \cfrac{0}{6}~~,~~\cfrac{24}{6} \right)\implies P=(0~~,~~4)\)
simplify √6+3√6
18√2
4√36
18
4√6
Answers
Answer:
Step-by-step explanation:
√6 + 3√6 = 4√6
Hope this helps
plz mark as brainliest!!!!!!
AT&T would like to test the hypothesis that the average revenue per retail user for Verizon Wireless customers is greater than $50. A random sample of 32 Verizon Wireless customers provided an average revenue of $54.70. It is believed that the population standard deviation for the revenue per retail user is $11.00. Using LaTeX: \alpha=0.05α = 0.05 , answer the following questions: a. Identify the null and alternative hypotheses to conduct an appropriate hypothesis test of mean. (3 points) b. Use the critical value approach to test this hypothesis. (3 points) State your decision and conclusions explicitly. (3 points) c. Use the p-value approach to test this hypothesis. (3 points) State your decision and conclusions explicitly. (3 points) d. Assume that the actual population mean for revenue per retail user is $44.30. Calculate the probability of type II error. (5 points)
Answers
Answer:
H0; u = 50 average revenue equals 50
H1: u not equal to 50, average revenue not equal to 50
This is 2 tailed
Alpha = 0.05
Z critical = 1.6449
We find the test statistics
Mean = 54.7
Sd = 11
n = 32
barX - u/sd/√n
= 54.70-50/11/√32
= 4.70/1.9435
= 2.418
Decision rule: reject H0 if test statistic > critical value. Accept if otherwise
2.418>1.6449
We reject H0
We conclude that average revenue is not equal to zero
C. P(z>=2.418) = 0.9922
1 - 0.9922
= 0.0078 (I used Ms excel here)
0.0078 < 0.05
So we Reject h0
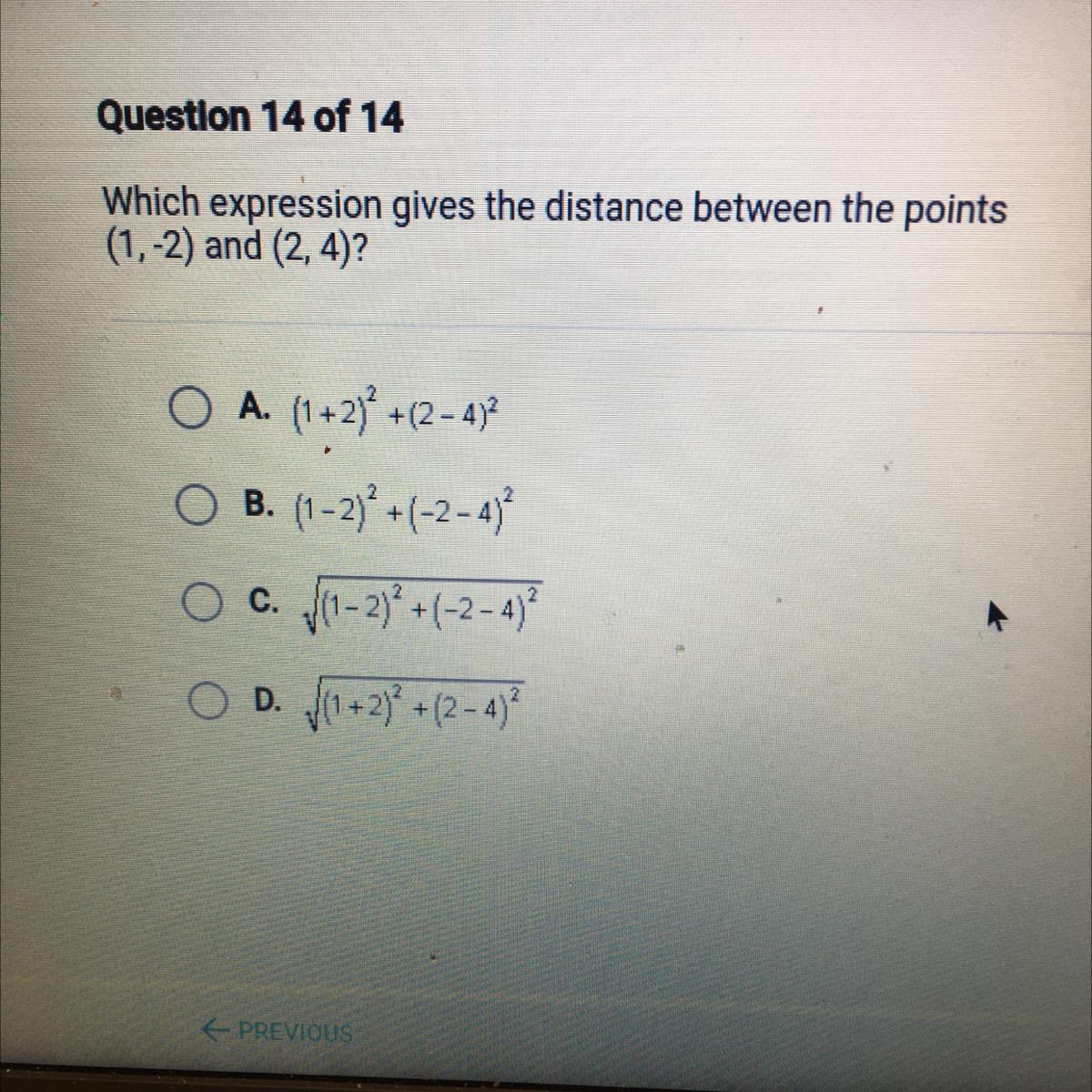
Question 14 of 14
Which expression gives the distance between the points
(1,-2) and (2, 4)?
O A. (1+23° +(2-47
O B. (1-2)*+(-2-4)
O c. 111-23 +4:32-47
O D. Hit+2y +(2-479
Answers
Answer:
c
Step-by-step explanation:
2. The absolute value function can be defined using piecewise notation. A(x) = { x > 0 -X, X < 0 Use this notation to find the following values: a. A(10) b. A(0) C. A(-3) d. A(3.14159) e. A(x) = 7 f. A(x) = -5 2a. 2b. 2c. 2d. 2e. 2f.

Answers
ANSWERS
a. A(10) = 10
b. A(0) = 0
c. A(-3) = 3
d. A(3.14159) = 3.14159
e. x = 7, x = -7
f. A(x) = -5 is not from this function
EXPLANATION
To find the answers to a to d we just have to write the number that inside the parenthesis as a positive number if it's negative.
For e the result is positive, so x can be either positive or negative:
\(\begin{gathered} x=7 \\ x=-7 \end{gathered}\)Result f does not belong to this function, because the function is always positive. If x is positive, then the value of the function is the same value of x. If x is negative, the value of the function is -x, hence this value is positive too.
what statements are true about this function

Answers
The true statement about the function is C. function f and function g are not inverse because f{g(x)} = g{f(x)} .
What is inverse of a function?An inverse function or an anti function, which can reverse into another function.In simple words, if any function “f” takes x to y then, the inverse of “f” will take y to x. If the function is denoted by 'f' or 'F', then the inverse function is denoted by f-1 or F-1.
now the given functions are,
f(x) = √(2x + 2) and
g(x) = (x^2 -2)/2
Now,
f{g(x)} = f{(x^2 -2)/2}
= √(2(x^2 -2)/2 + 2)
= √ x^2 -2 + 2
f{g(x)} = √ x^2
f{g(x)} = x
Now,
g{f(x)} = g{ √(2x + 2)}
= (√(2x + 2)^2 -2)/2
= (2x + 2) -2 /2
= 2x/2
f{g(x)} = x
Here we see that ,
f{g(x)} = g{f(x)}
Hence f and g are not inverses.
∴The true statement about the function is C. function f and function g are not inverse because f{g(x)} = g{f(x)} .
More about inverse of functions :
https://brainly.com/question/2541698
#SPJ2
3. You get three summer jobs to help you save for college expenses. In your job as a cashier,
you work 20 hours per week and earn $9.50 per hour. Your second and third jobs are at a local
hospital. There, you earn $9.00 per hour as a payroll clerk and $7.00 per hour as an aide. You
always work 10 hours less per week as an aide than you do as a payroll clerk. Your total weekly
salary depends on the number of hours you work at each job.
a. Determine the input and output variables for this situation.
b. Explain how you calculate the total amount earned each week.
c. If x represents the number of hours you work as a payroll clerk, represent the number of
hours you work as an aide in terms of x.
d. Write an equation that describes the total amount you earn each week. Use x to represent
the input variable and y to represent the output variable. Simplify the expression as much
as possible.
e. If you work 12 hours as a payroll clerk, how much will you make in one week?
f. What are the practical replacement values for x? Would 8 hours at your payroll job be a
realistic replacement value? What about 50 hours?
g. When you don't work as an aide, what is your total weekly salary?
Please help!
Answers
Hence the output variable (total weekly earnings) is a function of the input variable (number of hours worked as a payroll clerk) and may be expressed by the equation y = 16x + 120.
What is a Variable?A variable is anything that may be altered in the context of a mathematical notion or experiment. Variables are frequently denoted by a single symbol. .
a. Input variables: hours worked as a cashier, payroll clerk, and assistant.
The total amount earned each week is the output variable.
b. To determine the weekly total, multiply the number of hours worked at each job by the hourly rate and put them together. As a result, the equation would be:
Total weekly wage = (hours worked as a cashier x cashier hourly rate) + (hours worked as a payroll clerk x payroll clerk hourly rate) + (hours worked as an aide x rate per hour as an aide)
c. The amount of hours worked as an assistant is always 10 hours fewer than that of a payroll clerk. Therefore, if x denotes the number of hours worked as a payroll clerk, then the number of hours worked as an assistant may be denoted as (x - 10).
d. The equation describing the total money earned each week is as follows:
(20 x 9.5) + (x x 9) + ((x - 10) x 7) = y
This expression is simplified as follows:
y = 190 + 9x - 70 + 7x
y = 16x + 120
Hence the output variable (total weekly earnings) is a function of the input variable (number of hours worked as a payroll clerk) and may be expressed by the equation y = 16x + 120.
f. The realistic replacement values for x would be determined by the maximum number of hours you may work at each job as well as the amount of time available to work. Working 8 hours as a payroll clerk may be a reasonable substitute value if you have restricted availability, but 50 hours is unlikely.
g. If you do not work as an aide, you may calculate your total weekly income by setting the number of hours worked as an aide to zero in the calculation for the total amount earned each week. This results in:
y = 16x + 120 + 0
y = 16x + 120
As a result, the total weekly wage would be determined only by the number of hours performed as a cashier and payroll clerk.
To know more about variable visit:
https://brainly.com/question/2466865
#SPJ1
pls help, my teacher told me to translate this as an assignment so pls help.
th3f1r5t345y4551gnm3ntf0r411th35t9d3nt5.
and also this to. th3l45td4y0f5ch00l15601n6t0b31n4wh1l3.
answer key. y=7 e=3 s=5 a=4 9=u i=1 o=0 z=2 g=6 8=b.
Answers
Answer:
the first easy assignment for aii the students
the first day of school is go in to be in a while
Step-by-step explanation:
1. Determine the intervals on which each function is increasing or
decreasing
(a) f(x) = x^3 - 11/2x^2 - 4x
Answers
Answer:
\(\text{$f(x)$ is increasing for $(-\infty, -\frac{1}{3})$ and $(4, \infty)$} \\ \text{$f(x)$ is decreasing for $(-\frac{1}{3}, 4)$}\)
Step-by-step explanation:
We have the function:
\(f(x)=x^3-\frac{11}{2}x^2-4x\)
And we want to determine the intervals for which the function is increasing or decreasing.
We will need to first find the critical points of the function. Note that our original function is continuous across the entire x-axis.
To find the critical points, we need to find the first derivative and then solve for the x. So:
\(f^\prime(x)=\frac{d}{dx}[x^3-\frac{11}{2}x^2-4x]\)
Differentiate:
\(f^\prime(x)=(3x^2)-\frac{11}{2}(2x)-(4) \\ f^\prime(x)=3x^2-11x-4\)
Set the derivative equal to 0 and solve for x:
\(0=3x^2-11x-4\)
Factor:
\(0=3x^2-12x+x-4 \\ 0=3x(x-4)+(x-4) \\ 0=(3x+1)(x-4)\)
Zero Product Property:
\(3x+1=0\text{ or } x-4=0 \\ x=-\frac{1}{3}\text{ or } x=4\)
Therefore, our critical points are -1/3 and 4.
We can thus sketch the following number line:
<————-(-1/3)——————————————(4)—————>
Now, let’s test values for the three intervals: less than -1/3, between -1/3 and 4, and greater than 4.
For less then -1/3, we can use -1. So, substitute -1 for x for our first derivative and see which we get:
\(f^\prime(-1)=3(-1)^2-11(-1)-4=3+11-4=10>0\)
The result is positive.
Therefore, for all numbers less than -1/3,f(x) is increasing (since its derivative is positive).
For between -1/3 and 4, we can use 0. Substitute 0 for our derivative:
\(f^\prime(0)=3(0)^2-11(0)-4=-4<0\)
The result is negative.
Therefore, for all numbers between -1/3 and 4, f(x) is decreasing (since its derivative is negative).
And finally, for greater than 4, we can use 5:
\(f^\prime(5)=3(5)^2-11(5)-4=16>0\)
The result is positive.
Therefore, for all numbers greater than 4, f(x) is increasing (since its derivative is positive.
Therefore:
\(\text{$f(x)$ is increasing for $x<-\frac{1}{3}$ and $x>4$}\\ \text{ $f(x)$ is decreasing for $-\frac{1}{3}<x<4$}\)
In interval notation:
\(\text{$f(x)$ is increasing for $(-\infty, -\frac{1}{3})$ and $(4, \infty)$} \\ \text{$f(x)$ is decreasing for $(-\frac{1}{3}, 4)$}\)
Which is the graph of the function f/x )= x 2 2x 3?; Which graph represents the function f/x )= 4 x?; How do you find a function on a graph?; Which is one of the transformations applied to the graph of f/x )= x2 to change it into the graph?
Answers
The graph of the function f(x) = x² + 2x + 3 is a parabola with vertex (-1, 2).
You can use the vertical line test on a graph to determine whether a relation is a function. If it is impossible to draw a vertical line that intersects the graph more than once, then each x-value is paired with exactly one y-value. So, the relation is a function.
Given, the function is f(x) = x² + 2x + 3
We have to find the graph of the function.
Let y = x² + 2x + 3
Put x = -3
y = (-3)² + 2(-3) + 3
= 9 - 6 + 3
= 9 - 3
y = 6
Put x = -2
y = (-2)² + 2(-2) + 3
= 4 - 4 + 3
y = 3
Put x = -1
y = (-1)² + 2(-1) + 3
= 1 - 2 + 3
= 4 - 2
y = 2
Put x = 0
y = (0)² + 2(0) + 3
= 0 + 0 + 3
y = 3
Put x = 1
y = (1)² + 2(1) + 3
= 1 + 2 + 3
= 3 + 3
y = 6
We can plot the graph using the points.
The graph of the function f(x) = x² + 2x + 3 is a parabola with vertex (-1, 2).
Learn more about graph of quadratic equation at :
https://brainly.com/question/16191913
#SPJ4

Suppose the prices of a certain model of new homes are normally distributed with a mean of 150,000. Use the 68-95-99.7 rule to find the percentage of buyers who paid between $149,000 and $151,000 if the standard deviation is $1000
Answers
The percentage of buyers is approximately 68.26% of buyers of new houses paid between \($149,000\) and \($151,000\) .
We are given that the prices of the new homes are normally distributed with a mean of \($150,000\) and a standard deviation of $1000.
Using the 68-95-99.7 rule, we know that: approximately 68% of the data falls within one standard deviation of the mean approximately 95% of the data falls within two standard deviations of the mean, approximately 99.7% of the data falls within three standard deviations of the mean.
In order to determine the proportion of customers who spent between $149,000 and , we must first determine the z-scores for these values:
z1 = (149,000 - 150,000) / 1000 = -1 z2 = (151,000 - 150,000) / 1000 = 1
Now, we can determine the proportion of data that falls between z1 and z2 using the z-table or a calculator. The region to the left of z1 is 0.1587, and the area to the left of z2 is 0.8413, according to the z-table. Thus, the region bounded by z1 and z2 is:
0.8413 - 0.1587 = 0.6826
We can get the percentage of consumers who spent between by multiplying this by 100% is \($149,000\) and \($151,000\):
0.6826 x 100% = 68.26%
Therefore, the standard deviation of customers who paid between is \($149,000\) and \($151,000\) for this model of new homes.
For such more questions on standard deviation
https://brainly.com/question/30557671
#SPJ11
what should be subtracted from 7/12+7/8 to obtain the multiplicated inverse of (4/3-4/9)
Answers
To find the subtracted value, we need to calculate the multiplicative inverse of (4/3 - 4/9) and then subtract it from the sum of 7/12 and 7/8.
First, let's find the multiplicative inverse of (4/3 - 4/9):
Multiplicative inverse = 1 / (4/3 - 4/9)
To simplify the expression, we need a common denominator:
Multiplicative inverse = 1 / ((12/9) - (4/9))
= 1 / (8/9)
= 9/8
Now, we need to subtract the multiplicative inverse from the sum of 7/12 and 7/8:
Subtracted value = (7/12 + 7/8) - (9/8)
To perform this calculation, we need a common denominator:
Subtracted value = (7/12 * 2/2 + 7/8 * 3/3) - (9/8)
= (14/24 + 21/24) - (9/8)
= 35/24 - 9/8
To simplify further, we need a common denominator:
Subtracted value = (35/24 * 1/1) - (9/8 * 3/3)
= 35/24 - 27/24
= 8/24
= 1/3
Therefore, subtracting 1/3 from the sum of 7/12 and 7/8 will give you the multiplicative inverse of (4/3 - 4/9).
Suppose you deposit $1500 in a savings account that pays interest at an annual rate of 3.5%. Non money is added or withdrawn from the account. How much will be in the account after 5 years? How much will be in the account after 20 years?
Answers
Answer:
5 years : 1781.52
20 years: 2984.68
Simplify
4(1 + 9x) thank you
Answers
Answer:
4+36x
Step-by-step explanation:
you multiply the number on the outside of the parentheses with the numbers in the inside of the parentheses.
4 times 1 = 4
4 times 9x = 36x
36x+4
Express the solution graphically of 1/4 (x-3) ≤ -2
Answers
Answer:
Step-by-step explanation:
x = 5
Solution of 1/4 (x-3) ≤ -2 is x ≤ 5 . The value of x will be less than or equal to 5 .
Graph is attached below.
Given,
1/4 (x-3) ≤ -2
Now,
Inequality : 1/4 (x-3) ≤ -2
Solve for x,
x - 3 ≤ -8
Take -3 from LHS to RHS.
-3 will be converted to 3 in RHS .
x ≤ -8 + 3
x≤ -5
The value of x will be less than or equal to -5.
The graph of inequality is attached below and represents the the value of x is less than or equal to 5 .
Know more about inequality,
https://brainly.com/question/28984017
#SPJ4

En la ciudad de Los Ángeles, California, la población hispana es de 6012300. Si consideramos que el índice de población mexicana es de 72.5%, ¿cuántos mexicanos viven en Los Ángeles?
Answers
There are approximately 4,357,068 Mexicans living in Los Angeles.
How many Mexicans live in Los Angeles, California?To calculate the number of Mexicans living in Los Angeles, we need to multiply the Hispanic population by the Mexican population rate: Mexican population = Hispanic population * Mexican population rate
Substituting values:
Mexican population = 6,012,300 * 0.725
Mexican population = 4,357,067.5
Therefore, there are approximately 4,357,068 Mexicans living in Los Angeles.
Full question:
'In the city of Los Angeles, California, the Hispanic population is 6012300. If we consider that the Mexican population rate is 72.5%, how many Mexicans live in Los Angeles.
Read more about Proportion
brainly.com/question/1496357
#SPJ1
Find the surface area of
the prism.

Answers
Answer:
\(\text{D. }464\:\mathrm{ft^2}\)
Step-by-step explanation:
The surface area of the prism consists of four rectangles and two trapezoids. The sum of the areas of these polygons will give the total surface area of the prism:
Rectangle 1 (top base): \(12\cdot 14=168\)
Rectangle 2 (bottom base): \(6\cdot 14 = 84\)
Trapezoids 1 and 2 (lateral): \(2\cdot 9 \cdot 4=72\)
Rectangles 3 and 4 (lateral): \(2\cdot 14\cdot 5=140\)
Thus the total surface area is equal to
\(168+84+72+140=\boxed{\text{D. }464\:\mathrm{ft^2}}\)
24,783 is invested, part at 15% and the rest 9%. If the interest earned from the amount invested at 15% exceeds the interest earned from the amount invested at 9% by $894.09, how much is invested at each rate?
Answers
If 24,783 is invested, part at 15% and the rest 9%. If the interest earned from the amount invested at 15% exceeds the interest earned from the amount invested at 9% by $894.09: 51,960 is invested at 15%, and 22,823 is invested at 9%.
How to find the amount invested?Let's x represent the amount invested at 15%
Let the amount invested at 9% = 24,783 - x.
Interest earned at 15% is 0.15 * x
Interest earned at 9% is 0.09 * (24,783 - x)
We can set up the equation: 0.15x = 0.09 * 24,783 - 0.09x + 894.09
Solving for x:
0.06x = 24,783 * 0.09 + 894.09
0.06x = 2223.47 + 894.09
0.06x = 3117.56
x = 51,960
So,
(24,783 - x)
24,783 - 51,960
= 22,823
Therefore 51,960 is invested at 15%, and 22,823 is invested at 9%.
Learn more about amount invested here:https://brainly.com/question/25300925
#SPJ1
on a line chart, you can change the of the vertical axis to provide more vertical space and a more dramatic slope to the lines.
Answers
we are allowed to change the vertical axis on a line chart.
why we need to change the vertical axis?suppose we have a large range of value needed to plot along the vertical and horizontal axis, but the current line chart cannot meet this demand. in such cases, we can customize the scales to provide more vertical and horizontal spaces.
what is dramatic slope?dramatic slopes are the steep slopes of a straight line calculated by vertical and horizontal coordinate of two points laying on it. By changing the vertical axis as well as the horizontal axis we can plot a graph of a straight line more properly and finally more dramatic slope is visible there.
hence, we can change the scale values on a line chart to meet the requirement of the plot.
to learn more about line chart visit the link:
https://brainly.com/question/29833410
What are the angle measures?

Answers
Answer:
m1 - 120
m2 - 60
m3 - 60
m4 - 60
m5 - 30
A triangle is 180 degrees. An equilateral triange's angles are all the same.
How long do animals live? Beluga whole 40 bengal tiger 10 elephant seal 20 giraffe 25 orangutan 35
Answers
The time period of the animals life cycles are,
⇒ Beluga whole = 35 years
⇒ Bengal tiger = 10 years
⇒ Elephant = 20 years
⇒ Giraffe = 25 years
⇒ Orangutan = 40 years
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
There are some animals and there ages.
Now,
Since, There are some animals and there ages are given.
Hence, The correct ages of the animals are,
⇒ Beluga whole = 35 years
⇒ Bengal tiger = 10 years
⇒ Elephant = 20 years
⇒ Giraffe = 25 years
⇒ Orangutan = 40 years
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
subtract these polynomials (x^2+5x+2)- (5x^2-x-2)
Answers
Step-by-step explanation:
Here,
the given polynomials are;
(x^2+5x+2)-(5x^2-x-2)
now, when we open bracket of second polynomial we get,
=x^2+5x+2-5x^2+x+2
combining like terms and simplifying them we get;
=x^2-5x^2+5x+x+2+2
=-3x^2+6x+4.
Therefore, the answer is-3x^2+6x+4 or, taking - (minus) commo it will be -(3x2-6x-4).
Hope it helps....
how much money deposited now will provide payment of Rs. 15000 at the end of each half year for 10 years, if interest is 16% compounded six-monthly
Answers
The interest is 16% compounded semi-annually, is Rs. 121,179.10.
To determine how much money needs to be deposited now to provide a payment of Rs. 15,000 at the end of each half year for 10 years, we will use the formula for the present value of an annuity.
Present value of an annuity = (Payment amount x (1 - (1 + r)^-n))/rWhere:r = interest rate per compounding periodn = number of compounding periodsPayment amount = Rs. 15,000n = 10 x 2 = 20 (since there are 2 half years in a year and the payments are made for 10 years)
So, we have:r = 16%/2 = 8% (since the interest is compounded semi-annually)Payment amount = Rs. 15,000Using the above formula, we can calculate the present value of the annuity as follows:
Present value of annuity = (15000 x (1 - (1 + 0.08)^-20))/0.08 = Rs. 121,179.10Therefore, the amount that needs to be deposited now to provide payment of Rs. 15,000 at the end of each half year for 10 years, if the interest is 16% compounded semi-annually, is Rs. 121,179.10.
For more such questions on semi-annually
https://brainly.com/question/30573341
#SPJ8