determine the number of arrangements of the letters in georgiatech such that all the e's are consecutive.
Answers
The number of arrangements of the letters in "georgiatech" with all the e's consecutive is 60,480.
To determine the number of arrangements of the letters in "georgiatech" such that all the e's are consecutive, we can treat the three e's as a single unit. So, we have 9 distinct letters: g, o, r, g, i, a, t, c, h, and the "eee" unit.
The total number of arrangements of these 9 letters is 9!. However, within the "eee" unit, the three e's can be arranged among themselves in 3! ways. Therefore, we need to divide the total number of arrangements by 3!.
Hence, the number of arrangements of the letters in "georgiatech" such that all the e's are consecutive is:
9! / 3! = 362,880 / 6
= 60,480
To know more about arrangements,
https://brainly.com/question/31962614
#SPJ11
Related Questions
Type an equation in the blank below that represents this information in the form of y=kx
Answers
Answer:
y = kx
y=5x
10 = 2k
and so on
the measure of the supplement of an angle is 39° more then the angle. find the measure of the angle and it’s supplement.
Answers
Step-by-step explanation:
s = a+39
s+a = 180
a+39+a = 180
2a = 180-39
2a = 141
the angle = 70.5°
the supplement = 109.5°
bodhi has a collection of 175 dimes and nickels. the collection is worth $13.30. which equation can be used to find n, the number of nickels in the collection? 0.1n 0.05(n – 175)
Answers
The equation that can be used to find the number of nickels in Bodhi's collection is 0.10(175 - n) + 0.05n = 13.30.
To find the equation that can be used to find the number of nickels in Bodhi's collection, let's break down the information provided.
We are given that Bodhi has a collection of 175 dimes and nickels, and the total value of the collection is $13.30. We need to find the equation to determine the number of nickels, represented by 'n', in the collection.
Let's start by assigning variables to the number of dimes and nickels. Let 'd' represent the number of dimes, and 'n' represent the number of nickels.
We know that the total number of dimes and nickels in the collection is 175, so we can write the equation:
d + n = 175
Next, we need to consider the value of the collection. We are told that the total value is $13.30. Each dime is worth $0.10 and each nickel is worth $0.05. So, the total value equation can be written as:
0.10d + 0.05n = 13.30
Now, we can rearrange the first equation to solve for 'd':
d = 175 - n
Substituting this value of 'd' into the second equation, we get:
0.10(175 - n) + 0.05n = 13.30
Simplifying this equation, we get:
17.50 - 0.10n + 0.05n = 13.30
Combining like terms, we have:
0.05n = 13.30 - 17.50
0.05n = -4.20
Dividing both sides of the equation by 0.05, we get:
n = -4.20 / 0.05
n = -84
Since the number of nickels cannot be negative, we discard this solution. Therefore, there is no valid solution for the number of nickels in the collection.
To learn more about nickels click here:
https://brainly.com/question/17127685#
#SPJ11
Write the ratio as a fraction in simplest form.
63 : 28
The ratio as a fraction in simplest form is
.
Answers
Answer:Thus, 9/4 is the simplified fraction for 63/28 by using the GCD or HCF method. Thus, 9/4 is the simplified fraction for 63/28 by using the prime factorization method. 94 is already in the simplest form. It can be written as 2.25 in decimal form (rounded to 6 decimal places).
The given ratio 63:28 can be expressed as the simplified fraction 9/4.
What is the fraction?A fraction is defined as a numerical representation of a part of a whole that represents a rational number.
The given ratio is following as:
63:28
To express this ratio as a fraction in simplest form, we can use the method of finding the greatest common divisor (GCD) or highest common factor (HCF) between the numerator and denominator.
The GCD/HCF of 63 and 28 is 7.
We can divide both the numerator and denominator by 7 to simplify the fraction:
⇒ (63 ÷ 7) / (28 ÷ 7) = 9/4
Therefore, the ratio 63:28 can be expressed as the simplified fraction 9/4.
Learn more about the fraction here:
brainly.com/question/10354322
#SPJ2
f(x) = 2x - 1 , x= 1/2, - 1/2
Answers
Answer:
p(1/2)= 0 , p(-1/2)= -2
Step-by-step explanation:
p(1/2)= 2(1/2)-1
= 1-1
= 0
p(-1/2) = 2(-1/2)-1
= -1-1
= -2
the following sum (6 8n2 (6 8n)5)(8n) (6 16n2 (6 16n)5)(8n) ⋯ (6 8nn2 (6 8nn)5)(8n) is a right riemann sum for a certain definite integral ∫b6f(x)dx using a partition of the interval [6,b] into n subintervals of equal length. then the upper limit of integration must be: b
Answers
The upper limit of integration, b, can be determined by examining the given right Riemann sum and its representation as a definite integral.
In the right Riemann sum, the interval [6, b] is divided into n subintervals of equal length. Each subinterval has a width of **8n** because it is multiplied by the function **(8n)**. The function **f(x)** is represented by the expression **(6 8nx2 (6 8nx)5)**, where **x** represents the variable of integration.
To find the upper limit of integration, we need to determine the value of **b**. Notice that in each term of the Riemann sum, the function is evaluated at the right endpoint of each subinterval. In this case, the right endpoint is given by **(6 + 8n)**, which is obtained by adding the width of the subinterval **(8n)** to the left endpoint **6**.
Since the interval [6, b] is divided into n subintervals, the total length of the interval is **n times the width of each subinterval**, which is **n * (8n)**. Thus, the upper limit of integration, **b**, is given by:
**b = 6 + n * (8n)**
This equation represents the relationship between the number of subintervals **n** and the upper limit of integration **b**.
In summary, the upper limit of integration, **b**, in the given right Riemann sum for the definite integral ∫b6f(x)dx using a partition of the interval [6, b] into n subintervals of equal length is determined by the equation **b = 6 + n * (8n)**.
Learn more about integral here
https://brainly.com/question/30094386
#SPJ11
Assume heights of the students in a class is a random variable (H) and follows a normal distribution with mean 66 in and standard deviation of ou=5 in. What is the probability that a student in this class has a height greater or equal to 74.6 in (i.e., P(H > 74.6)). (You can use the following table which presents the cumulative distribution function of the Standard Normal distribution.) a) 0.0427 Ob) 0.1587 O 0.4212 O d) 0.6554
Answers
To find the probability (P(H > 74.6)), calculate the cumulative probability of the standard normal distribution for the z-score corresponding to 74.6 inches.
First, we calculate the z-score using the formula: z = (x - μ) / σ, where x is the given value, μ is the mean, and σ is the standard deviation. In this case, the z-score is (74.6 - 66) / 5 = 1.72. Next, we look up the cumulative probability in the standard normal distribution table corresponding to a z-score of 1.72. From the table, we find the cumulative probability to be approximately 0.9564. Since we want the probability of heights greater than 74.6 inches, we subtract the cumulative probability from 1: 1 - 0.9564 = 0.0436.
Therefore, the probability that a student in this class has a height greater than or equal to 74.6 inches is approximately 0.0436, which is approximately equal to 0.0427 (rounded to four decimal places). So the answer is option (a) 0.0427.
To learn more about probability click here: brainly.com/question/31828911
#SPJ11
Select all the values of x that make the equation | 3x + 4 | − 9 = 0 true.
A . 1 2/3
B. -1 2/3
C. 4 1/3
D. -4 1/3
E. 5 2/3
F. -5 2/3
Answers
\(|3x+4|-9=0\)
Add 9 to both sides:
\(|3x+4|-9+9=0+9\)
\(|3x+4|=9\)
Solve the Absolute Value:
\(3x+4=9or3x+4=-9\)
__________________________________________________________
\(3x+4=9\)
Subtract 4 from both sides:
\(3x+4-4=9-4\)
\(3x=5\)
Divide both sides by 3:
\(\dfrac{3x}{3} =\dfrac{5}{3}\)
\(\fbox{x = $\dfrac{5}{3} $ or 1$\dfrac{2}{3}$}\)
__________________________________________________________
\(3x+4=-9\)
Subtract 4 from both sides:
\(3x+4-4=-9-4\)
\(3x=-13\)
Divide both sides by 3:
\(\dfrac{3x}{3} =\dfrac{-13}{3}\)
\(\fbox{x = $\dfrac{13}{3} $ or -4$\dfrac{1}{3} $}\)
________________________________________________________
\(\fbox{Options A and D}\)
please help........
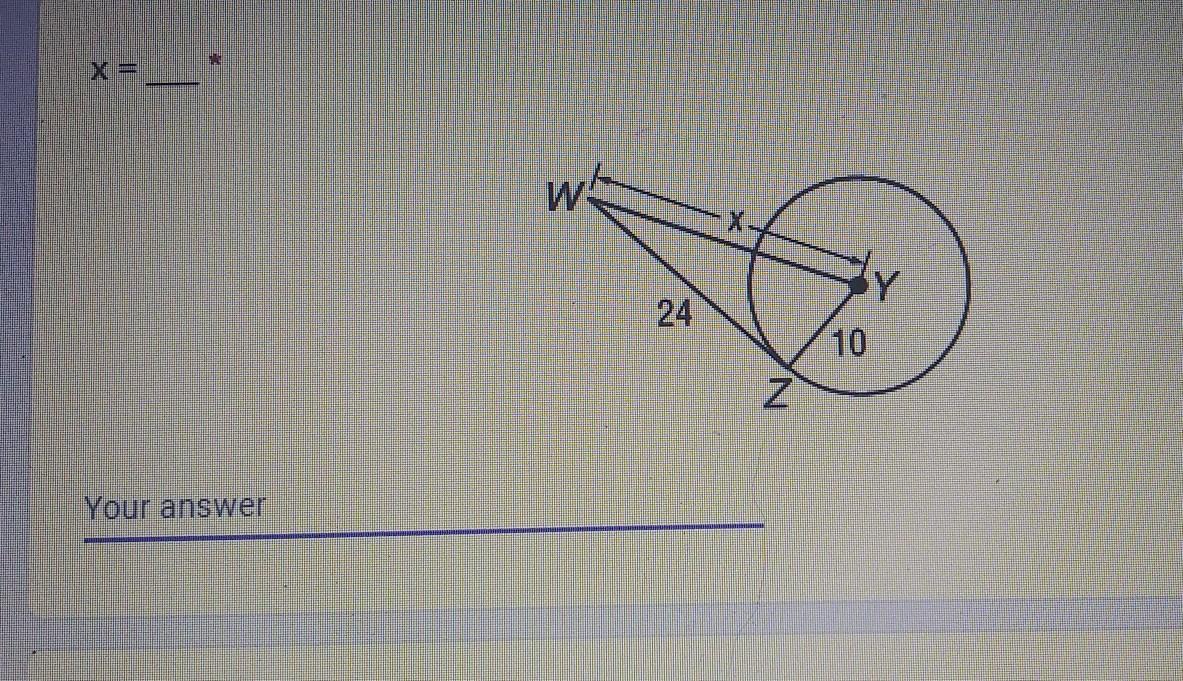
Answers
x = √(10²+24²)
= √(100+576)
=√(676)
= 26.
Answer:
26
Step-by-step explanation:
since wz is a tangent to the circle then measure angle wzy equal 90° so you will be using Pythagoras therom then X = (24)^2 + (10)^2 all under a square root as it's a hypotenuse
please help! no wrong answers or I will report :)

Answers
Answer:
a. (1, 1)
Step-by-step explanation:
plug into equation: 5(1)+ 4(1) less than or equal to 10
solve: 5+4=9 and 9 is less than 10
The measures of the angles of a triangle are shown in the figure below. Solve for x.

Answers
The value of x will be 6° according to the remaining angles values in the diagram.
What is a Triangle?
With three sides, three angles, and three vertices, a triangle is a closed, two-dimensional object. A polygon also includes a triangle.
How are the sum of triangles calculated in a triangle?
In a triangle, the total interior angles are supplementary. In other words, the sum of a triangle's inner angle measurements is 180°. Hence, we can write the triangle sum theorem's formula as A + B + C = 180° for the triangle ABC.
Now according to the question
=> 40+110+8x-18=180 (Theorem)
=> 150+8x-18=180
=> 8x=180-150+18
=> 8x=48
=> x=6°
The value of x will be : 6°
To know more about triangles visit:
https://brainly.com/question/2773823
#SPJ1
1) Marcos deseja comprar uma guitarra. Seu amigo possui um e quer vender a vista por R$850,00. Caso Marcos prefira, pode parcelar em 4 parcelas iguais, com vencimento para 30, 60, 90 e 120 dias, seu amigo aplicará sobre o valor do produto, uma taxa única de 12%. Nessa situação, o custo final da guitarra e o valor de cada parcela são respectivamente: *
1 ponto
a) R$102,00 e R$55,00.
b) R$850,00 e R$212,00
c) R$952,00 e R$238,00
d) R$980,00 e R$245,00.
2) Luiza está em dúvida sobre financiar uma moto nova no valor de R$25.000,00 ou fazer um consórcio. Como o desejo de Luiza em adquirir uma moto é algo que tem a mais de dois anos, ela já dispõe de uma reserva, aplicada na caderneta de poupança, de R$15.000,00. As propostas que lhe foram apresentadas na concessionária são: Financiamento de 36 prestações fixas de R$1.050,00 sem entrada.Financiamento de 36 prestações fixas de R$395,00 com entrada de R$14.000,00.Consórcio de 36 prestações reajustáveis de acordo com a inflação, sendo a primeira parcela no valor de R$800,00, com possibilidade de obter a moto, ao longo do período do consórcio, por meio de sorteio ou lance.Das opções apresentadas a mais vantajosa para Luiza é: *
1 ponto
a) O consórcio, pois, a prestação não é tão alta e ela ainda terá o valor de suas economias para usar em caso de alguma emergência.
b) O financiamento de 36 prestações fixas de R$1.050,00 sem entrada.
c) O financiamento de 36 prestações de R$395,00 fixas com entrada de R$14.000,00.
d) Todas as propostas são equivalentes, Luiza pode escolher qualquer uma delas.
Answers
Answer:
1)C
2)C
Step-by-step explanation:
Fiz no Classroom!!!
Mr. A sold his land to Mr.B at a profit of 10%. Mr.B. sold it to Mr.C at a gain of 5%. Mr.C.paid N1240 more for the house than Mr. A paid. What did Mr. A paid.
Answers
Answer:
Mr. A initially paid approximately N8000 for the land.
Step-by-step explanation:
Step 1: Let's assume Mr. A initially purchased the land for a certain amount, which we'll call "x" in currency units.
Step 2: Mr. A sold the land to Mr. B at a profit of 10%. This means Mr. A sold the land for 110% of the amount he paid (1 + 10/100 = 1.10). Therefore, Mr. A received 1.10x currency units from Mr. B.
Step 3: Mr. B sold the land to Mr. C at a gain of 5%. This means Mr. B sold the land for 105% of the amount he paid (1 + 5/100 = 1.05). Therefore, Mr. B received 1.05 * (1.10x) currency units from Mr. C.
Step 4: According to the given information, Mr. C paid N1240 more for the land than Mr. A paid. This means the difference between what Mr. C paid and what Mr. A paid is N1240. So we have the equation: 1.05 * (1.10x) - x = N1240
Step 5: Simplifying the equation: 1.155x - x = N1240
Step 6: Solving for x: 0.155x = N1240
x = N1240 / 0.155
x ≈ N8000
Therefore, in conclusion, Mr. A initially paid approximately N8000 for the land.
is y^8=2xX a function
Answers
No, the equation\(y^{8}\)=2xX is not a function.
What is Function?
In mathematics, a function is a relation between a set of inputs (also known as the domain) and a set of possible outputs (also known as the range), with the property that each input is related to exactly one output. In other words, a function is a rule that assigns each input value to a unique output value.
A function is a relation between a set of inputs and a set of possible outputs, with the property that each input is related to exactly one output. In other words, for a relation to be a function, each input must produce only one output.
In the equation\(y^{8}\)=2xX, there are multiple possible values of y for each value of x. For example, if x=1, then y can be either \(2^{(1/8)}\) or -\(2^{(1/8)}\), which means that x is not related to a unique value of y. This violates the definition of a function, which requires each input to produce only one output.
Therefore, \(y^{8}\)=2xX is not a function.
Learn more about Function
https://brainly.com/question/11624077
#SPJ1
jane is 3 times as old as kate. in 5 years jane's age will be 2 less than twice kate's. how old are the girls now
Answers
Answer:
Kate is 3 years old, Jane is 9 years old
Step-by-step explanation:
1.) First, assign variables to all of their ages. If we say Kate's age is x, Jane's age is 3 times this, which can be written as j, is 3x.
2.) Jane's age is also 2 less than twice of Kate's in 5 years. This means that her age is also 2(x+5) - 2 = j + 5. With a little simplification, you get that 2x + 8 = j + 5.
3.) Since j, Jane's age, is also 3x, we can substitute 3x in for j in the second equation. If you do this, you get 2x + 8 = 3x + 5.
4.) By moving the x onto one side and the numbers onto another, you get x = 3. X was Kate's age, meaning that Kate is 3 years old.
5.) Finally, since Jane's age is 3 times Kate's age, Jane's age is 3 * 3, which is 9. Jane is 9 years old.
Jane is 9 years old and Kate is 3 years old.To solve the problem, let's first establish variables for Jane and Kate's ages.
Let J represent Jane's age and K represent Kate's age.
According to the student question, Jane is 3 times as old as Kate, which can be represented as:
J = 3K
In 5 years, Jane's age will be 2 less than twice Kate's age, which can be represented as:
J + 5 = 2(K + 5) - 2
Now we can solve the equations step by step:
Substitute the first equation into the second equation to eliminate one of the variables:
3K + 5 = 2(K + 5) - 2
Distribute the 2 on the right side of the equation:
3K + 5 = 2K + 10 - 2
Simplify the equation by combining like terms:
3K + 5 = 2K + 8
Move the 2K term to the left side of the equation:
K = 3
now we know that Kate is currently 3 years old.
Substitute K's value back into the first equation to find Jane's age:
J = 3K
J = 3(3)
Simplify to find Jane's age:
J = 9
So, Jane is currently 9 years old.
Jane is 9 years old and Kate is 3 years old.
for more questions on variables
https://brainly.com/question/9302141
#SPJ11
After 50 years, Helena's age will be three times her age now. How old is Helena now?
Answers
Answer:
25
Step-by-step explanation:
n + 50 = 3n
25 + 50 = 75
hope this helps...
PLZ NEED HELP ASAP whats the answer???

Answers
Answer:
28in
Step-by-step explanation:
you can use bar models to find this.
there would be 2 bars, one with 5 units and another with 1
that means you divide the total by 6 to find the value of the singular unit, which would be the shorter piece.
equation of the line that passes through the points (7, 6) and (-2, -3)?
Answers
Answer:
y=x-1
Step-by-step explanation:
Hi there!
We want to find the equation of the line that passes through the points (7, 6) and (-2, -3)
There are 3 ways to write the equation of the line:
Slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept Point-slope form, which is \(y-y_1=m(x-x_1)\), where m is the slope and \((x_1, y_1)\) is a pointStandard form, which is ax+by=c, where a, b, and c are free integer coefficients, but a and b cannot be 0, and a cannot be negativeThe most common (and usually, the easiest way) would be slope-intercept form, so let's write it that way
First, we'll need to find the slope of the line
The slope can be found using the formula \(\frac{y_2-y_1}{x_2-x_1}\), where \((x_1, y_1)\) and \((x_2, y_2)\) are points
We have two points, which is needed, but let's label their values in order to avoid any confusion:
\(x_1= 7\\y_1=6\\x_2=-2\\y_2=-3\)
Now substitute these values into the formula to find the slope (m):
m=\(\frac{y_2-y_1}{x_2-x_1}\)
m=\(\frac{-3-6}{-2-7}\)
Subtract the numbers
m=\(\frac{-9}{-9}\)
Divide
m=1
The slope of the line is 1
So far, we can write the equation of the line as this:
y=1x+b, or y=x+b
We'll need to find b
As the equation passes through both (7,6) and (-2, -3), we can use either one of them to solve for b
Taking (7, 6) for instance, substitute 7 as x and 6 as y:
6=1(7)+b
Multiply
6=7+b
Subtract 7 from both sides
-1=b
Now substitute -1 as b:
y=x-1
Hope this helps!
What is the decimal value of 1101(base 2)?
Answers
The decimal value of 1101 (base 2) is 13.
To find the decimal value, follow these steps:1. Identify the place values of each digit. In this case, from right to left, the place values are 2^0, 2^1, 2^2, and 2^3.
2. Multiply each digit by its corresponding place value.
1 * 2^3 = 1 * 8 = 8
1 * 2^2 = 1 * 4 = 4
0 * 2^1 = 0 * 2 = 0
1 * 2^0 = 1 * 1 = 1
3. Add the results of the previous step together: 8 + 4 + 0 + 1 = 13.
So, the decimal value is 13.
Learn more about Decimal:
https://brainly.com/question/28393353
#SPJ11
A cylinder has a base radius of 7in and a height of 18in. What is its volume in cubic in, to the nearest tenths place?
Answers
The cylinder has a height of 18 in, a base radius of 7 in, and a volume of 2769.5 in³.
How can you figure out a cylinder's volume?A cylinder is one of the most basic curvilinear geometric shapes and has traditionally been a solid in three dimensions. In elementary geometry, it is regarded as a prism with a circle as its basis.
V = πr²h is the formula for computing a cylinder's volume.
where ;
r is the radius 7 inches and;h is the height 18 inches.Replace the specified arguments to obtain:
V = π(7)² * 18
V = 2769.5 in³
Therefore, the cylinder's volume, which has a base radius of 7 inches and a height of 18 inches, is 2769.5 in³.
Find out more about cylinder volume here: https://brainly.com/question/9554871
#SPJ1
A bag contains 77 coins consisting of quarters and nickels. The total value of the coins is $12.50. Write a system of equations that can be used to determine the number of quarters, x, and the number of nickels, y, in the bag. a x + y = 77 0.25x + 0.5y = 12.5 b 0.25x +0.5 y = 77 x + y = 12.5 c x + y = 77 0.25x + 0.05y = 12.5 d 0.25x + 0.05y =77 x + y = 12.5
Answers
Answer:
A
Step-by-step explanation:
because the answer needs both amounts of money and the beginning equation x + y = 77 can't have any other numbers.
what is cme 303 2018
Answers
CME 303 is a course offered at Stanford University that focuses on modeling, simulation, and optimization of complex systems.
It is an introduction to the fundamentals of mathematical optimization, which deals with the problem of finding the best solution to a given problem. The course covers basic optimization theory and algorithms, including linear programming, integer programming, nonlinear programming, dynamic programming, and stochastic programming. Furthermore, it introduces optimization software packages, such as MATLAB, GAMS, and CPLEX, and how to use them for solving real-world optimization problems. It also covers the application of optimization techniques to areas such as finance, engineering, economics, and computer science.CME 303 is a course offered at Stanford University that focuses on modeling, simulation, and optimization of complex systems. The course is taught using lectures, tutorials, and computer lab assignments. In the final project, students apply the techniques learned in the course to solve a real-world problem.
Learn more about complex systems here:
https://brainly.com/question/26671074
#SPJ4
Hello I need help on this math question
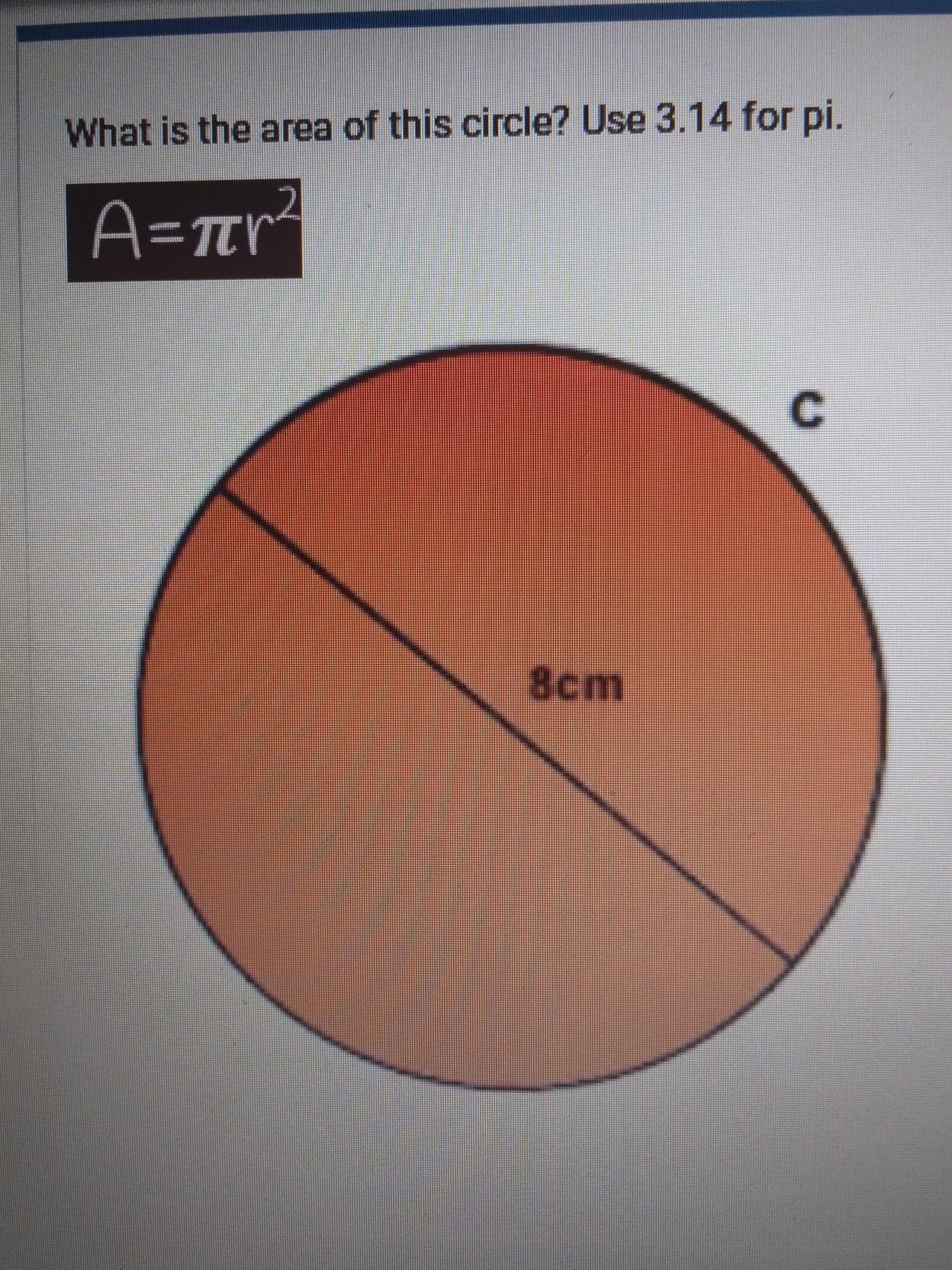
Answers
Answer:
\(50.24\ cm ^2\)
Step-by-step explanation:
Let's start by finding the radius of this circle.
\(D=2r\\8=2r\\\text{Divide both sides by 2}\\r=4\)
Note that in the equation:
\(A=\pi r^2\)
"A" stands for area and "r" stands for radius.
Now, let's substitute the given values into the equation.
\(A=\pi r^2\\A=3.14*(4)^2\\A=3.14*16\\A=50.24\ cm^2\)
The two-point forward difference requires two nodes to approximate the derivative. 2. The two-point forward difference always requires two consecutive nodes to approximate the derivative. 3. The three-point forward difference requires three consecutive nodes to approximate the derivative.
Answers
The statements are as follows: The two-point forward difference requires two nodes to approximate the derivative. (True)
The two-point forward difference always requires two consecutive nodes to approximate the derivative. (False)
The three-point forward difference requires three consecutive nodes to approximate the derivative. (True)
The two-point forward difference method indeed requires two nodes to approximate the derivative. This method calculates the derivative using the difference between the function values at two neighboring points.
The two-point forward difference method does not always require two consecutive nodes. It can be used with any two nodes, regardless of whether they are consecutive or not. However, using consecutive nodes is a common and straightforward approach.
The three-point forward difference method requires three consecutive nodes to approximate the derivative. It calculates the derivative using the difference between the function values at three consecutive points. This method provides higher accuracy compared to the two-point forward difference method.
Learn more about derivative from
https://brainly.com/question/12047216
#SPJ11
Find the measure of angle n.
a
90°
b
61°
c
29°
d
119°

Answers
Answer:
c
Step-by-step explanation:
What is the solution to this equation?
9 ^x- 1 = 2
O A. 1
O B. 2
O C.
1/2
OD. -1/2

Answers
Add 1 to both sides
Take log of both sides
X=log 3(3)/log 3 (9)
Solve
Solution
X=1/2
Write an expression using fractions to determine the amount that each person will pay then calculate each person's contributions showing all steps in long division
Answers
Answer:
Fractional Expression for how much each person pays = (64.04/4)
Each person pays $16.01.
Step-by-step explanation:
Complete Question
Write an expression using fractions to show how to determine the amount that each person will pay. Then calculate each person's contributions showing all steps in long division.
The total of the bill is $64.04 and there are 4 people splitting the bill.
Solution
Total amount to be shared equally by 4 persons = $64.04
Fractional Expression for how much each person pays = (64.04/4)
Long division method to do this division.
16.01
4 | 64.04
4
24
24
00
0
04
4
0
Each person pays $16.01.
Hope this Helps!!!
Write the inverse of the function f (x) = eˣ⁻⁷. Use In or log if appropriate. f⁻¹ (x) =
Answers
The inverse of the function, f⁻¹(x) = -7ln(x).
To find the inverse of the function f(x) = \(e^{x^{-7} }\) , we can proceed as follows:
Step 1: Replace f(x) with y:
y = \(e^{x^{-7} }\)
Step 2: Swap x and y:
x = \(e^{y^{-7} }\)
Step 3: Solve for y:
Take the natural logarithm (ln) of both sides:
ln(x) = ln( \(e^{y^{-7} }\) )
Apply the property of logarithms that ln(\(e^{a}\)) = a:
ln(x) = y⁻⁷
Step 4: Solve for y:
Multiply both sides by -7:
-7ln(x) = y
So, the inverse function f⁻¹(x) is:
f⁻¹(x) = -7ln(x)
Therefore, the inverse of the function f(x) = \(e^{x^{-7} }\) is f⁻¹(x) = -7ln(x).
To learn more about inverse here:
https://brainly.com/question/29141206
#SPJ4
Please help!!! geometry

Answers
Answer:
17
1234
4567
56783
56743
given the following probabilities, for what P(B)
are events A
and B
independent?
P(A)=34
P(A and B)=14
Answers
Events A and B are independent if P(B) is equal to 1/3 when P(A) = 3/4 and P(A and B) = 1/4. Otherwise, A and B are not independent.
To determine if events A and B are independent, we need to compare the probability of the intersection of A and B, P(A and B), with the product of the individual probabilities of A and B, P(A) and P(B).
If events A and B are independent, then the occurrence of event A should not affect the likelihood of event B, and vice versa. In this case, the equation for independent events would be:
P(A and B) = P(A) * P(B)
Given that P(A and B) = 1/4 and P(A) = 3/4, we can substitute these values into the equation:
1/4 = (3/4) * P(B)
To solve for P(B), we can isolate the variable:
P(B) = (1/4) / (3/4) = 1/3
Therefore, events A and B are independent if and only if P(B) = 1/3.
In conclusion, for events A and B to be independent, the probability of event B, denoted as P(B), should be equal to 1/3 when P(A) = 3/4 and P(A and B) = 1/4. If P(B) takes any other value, events A and B would not be considered independent.
For more question on independent visit:
https://brainly.com/question/29863918
#SPJ8