Determine the half range fourier Cosine series up to 3
harmonics.
f(t) = t^2 , t[0 ,2] , where f(t +4) =f(t)
Answers
The half-range Fourier cosine series of the function f(t) = t^2 over the interval t ∈ [0, 2], with f(t + 4) = f(t), can be determined by finding the coefficients for the cosine terms up to the 3rd harmonic.
The Fourier series representation of f(t) is given by f(t) = a₀/2 + Σ(aₙ cos(nωt)), where a₀/2 represents the average value and aₙ are the coefficients.
To calculate the coefficients, we first find the average value a₀/2. Since f(t) is an even function, the average value can be calculated as a₀/2 = (2/2) ∫₀² t² dt. Evaluating this integral, we get a₀/2 = 4/3.
Next, we determine the coefficients aₙ for the cosine terms. The formula for aₙ is given by aₙ = (2/L) ∫₀² f(t) cos(nπt/L) dt, where L is the period of the function. In this case, L = 4 since f(t + 4) = f(t).
For the 1st harmonic (n = 1), the coefficient a₁ can be calculated as a₁ = (2/4) ∫₀² t² cos(πt/4) dt. Evaluating this integral, we find a₁ = 32/π².
Similarly, we can find the coefficients for the 2nd (n = 2) and 3rd (n = 3) harmonics using the respective formulas and integrals.
In summary, the half-range Fourier cosine series up to the 3rd harmonic for the function f(t) = t^2, t ∈ [0, 2], with f(t + 4) = f(t) is given by f(t) = (4/3) + (32/π²)cos(πt/4) + (64/π²)cos(πt/2) + (32/π²)cos(3πt/4).
To learn more about Fourier series: -brainly.com/question/31705799
#SPJ11
Related Questions
Which of the following numbers are less than-0.625. The numbers are -8/5 -5/8 -0.5 choose all that apply
Answers
Answer:
-8/5 = -1.6
-5/8 = -0.625
-1/2 = --0.5
Step-by-step explanation:
The number that is less then -0.625 is -8/5 which is -1.6
If f(x) and it’s inverse function, f^-1(x), are, both plotted on the same coordinate plane, what is their point of intersection
Answers
Answer:
Step-by-step explanation:
Hello,
there is not always an intersection point
let's take the example of on the appropriate domain
\(f(x)=e^x \ \ \ f^{-1}(x)=ln(x)\)
there is no intersection point
if there is one it means that the point (x,f(x)) and the point (x,\(f^{-1}(x)\)) is the same so that have to solve
\(f(x)=f^{-1}(x)\)
for instance if we take
\(f(x)=x^2 \ \ \ f^{-1}(x)=\sqrt{x} \ \ \ for \ x >= 0\)
intersection point are for x >= 0
\(x^2=\sqrt{x} <=>x^4=x<=>x^3=1 \ or \ x=0<=> x = 1 \ or \ x=0\)
hope this helps
Answer:
D
Step-by-step explanation:
please help I’m stuck on this question !!
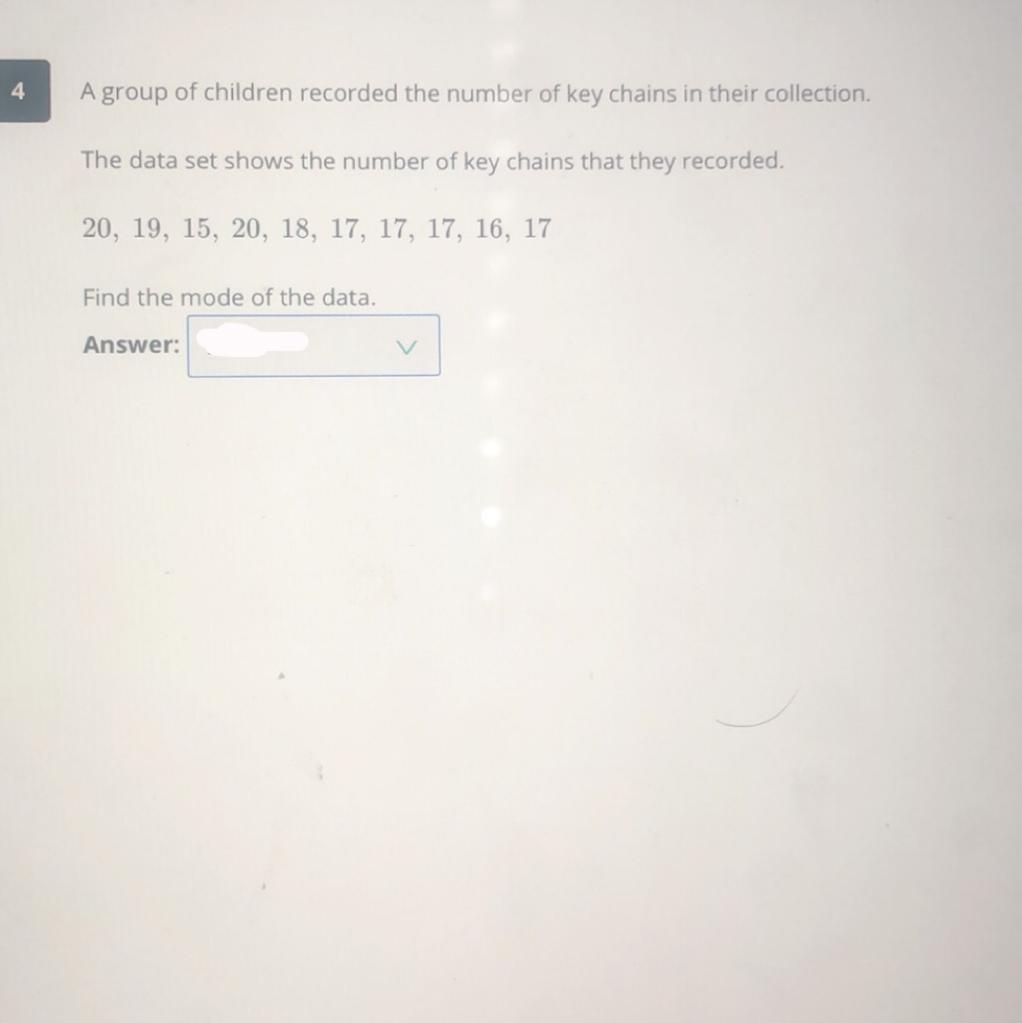
Answers
Answer:
mode: 17
Step-by-step explanation:
mode is the number that appears the most in a set of data.So the answer is 17
You have just signed up for a broadband home internet service that uses coaxial cable. which connector type will you most likely use?
Answers
Answer:
F type connector
Step-by-step explanation:
Use an F-type connector for broadband cable connections that use coaxial cable.
The F connector is a coaxial RF connector commonly used for "over the air" terrestrial television, cable television and universally for satellite television and cable modems,
#SPJ4
Learn more on
https://brainly.com/question/14391417
F type connector
The F-connector is a coaxial RF connector commonly used for "wireless" terrestrial television, cable television, and common for satellite television and cable modems, usually with RG-6/U cable or with RG -59 / U.F connector is also known as threaded connector. There are two main types: 7mm (6.8mm) is the most common and used in coaxial cable, and 5mm connector is used in thin coaxial cable commonly used in satellite system.
The F-connector is an accessory that connects a coaxial cable to an electronic device or wall outlet.
Type F connectors are highly mechanical and electrically stable coaxial screw connectors for cable television (CATV), set-top boxes, cable modems and satellite television applications up to 4 GHz
Learn more about wire here
https://brainly.com/question/15246898
#SPJ4
Write algebraic expressions for two numbers with a sum of -13. Let one of the numbers be represented by x. If one number is represented by x, how would the other number be represented?
Answers
Answer:
If a sum of 2 numbers is -7 and one is x then you can write it down as X + Y = -7, or you can write it then ... Let one of the number be represented by x.
The area of the shaded sector is 5 pi square meters. What is the area of the entire circle? Express your answer in terms of Pi.
A circle. The shaded section has an angle measure of 100 degrees.
Recall that StartFraction Area of sector over area of circle EndFraction = StartFraction n degrees over 360 degrees EndFraction.
A) 12 pi
B) 14 pi
C) 18 pi
D) 20 pi
Answers
Answer:
C - 18 pi
Step-by-step explanation:
edge
Answer:
5/18
108
A sector has an area of 30π in.2. The radii containing the sector form an angle of 100°. What is the area of the circle?
The ratio of the angle of the sector to the entire circle is
✔ 5/18
.
Area of the sector = StartFraction n degrees over 360 degrees EndFraction (pi) (r squared). 30 pi = StartFraction 100 degrees over 360 degrees EndFraction (pi) (r squared). (StartFraction 18 over 5 EndFraction) 30 pi = (pi) r squared.
The area of the entire circle is
✔ 108
Pi in.2
in a box of 10 electrical parts, 2 are defective. (a) if you choose one part at random from the box, what is the probability that it is not defective? (b) if you choose two parts at random from the box, without replacement, what is the probability that both are defective?
Answers
The probabilities are :
a) 0.8
b) 1/45
Probability refers to potential. This branch of mathematics deals with the occurrence of a random event. The value's range is 0 to 1. Probability has been applied into mathematics to predict the likelihood of different events.
Total no. of electrical parts = 10
No. of defective parts = 2
No. of non-defective parts = 10 - 2
= 8
a) The probability of choosing a non-defective part from the box is 8/10 or 0.8.
b) The probability of choosing two defective parts in a row without replacement is (2/10) * (1/9) = 2/90 = 1/45.
To learn more about probabilities here:
https://brainly.com/question/30034780
#SPJ4
i need one more smart person plezzz

Answers
Answer:
Interior: 135 degrees
Exterior: 45 degrees
Step-by-step explanation:
The interior angle of a regular octagon is exactly 135 degrees, which can be found using the (n – 2)180 formula. The exterior is simply 180 - the interior, which is 45. :)
Answer:
whadda say
Step-by-step explanation:
interior angle: (n-2)×180°
exterior angle: (n-2)÷180°
find the unknown size of angle
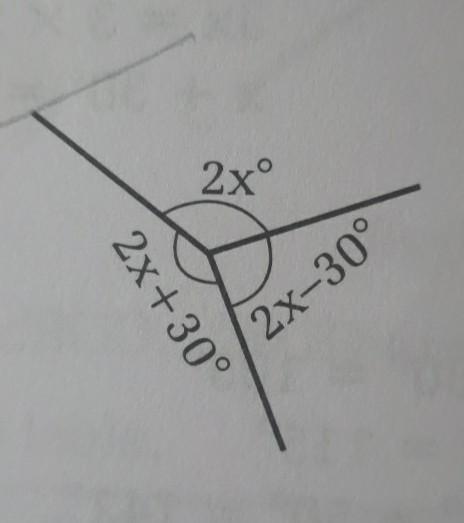
Answers
Answer:
x = 60
2x = 120
2x + 30 = 150
2x - 30 = 90
Step-by-step explanation:
2x + 2x - 30 + 2x + 30 = 360
2x + 2x + 2x + 30 - 30 = 360
6x + 0 = 360
6x = 360
x = 360 / 6
x = 60
2x
= 2 x 60
= 120
2x + 30
= 120 + 30
= 150
2x - 30
= 120 - 30
= 90
What is the least common multiple of 24 and 40?
960
80
120
240
Answers
Answer:
120
Step-by-step explanation:
Answer:
120 is the answer
use the step-ladder method
I need help with how to write the expressions in its simplest form which is 15 and I also need help with 16

Answers
Recall that like terms are terms that have the same variables and powers. The coefficients of the terms do not have to match.
a.- Notice that 4z and -3z are like terms since they have the same variables with the same exponents, therefore:
\(4z-3z=(4-3)z=1z=z\text{.}\)b.- Notice that 3n and -3n are like terms, but 6 is a constant, therefore:
\(6-3n+3n=6+(-3+3)n=6+0n=6.\)c.- In the given expression, the similar terms are 2g and -8g, and -3 and 11, therefore:
\(2g-3+11-8g=(2-8)g+(-3+11)=-6g+8.\)d.- In the last expression, first, we have to apply the distributive property:
\(3(4x-5)+4(2x+6)=12x-15+8x+24.\)Now, adding like terms we get:
\(12x-15+8x+24=20x+9.\)Answer:
a.-
\(z\text{.}\)b.-
\(6.\)c.-
\(-6g+8.\)d.-
\(20x+9.\)I will give brainliest to the person who does this first

Answers
1. 8a+24
2. .12e
ill edit it when get the other answers
Brainiest? pls
1. Classify the two given samples as independent or dependent. Sample 1: Pre-training weights of 19 people Sample 2: Post-training weights of the same 19 people A) dependent B) independent 2. As part of a marketing experiment, a department store regularly malled discount coupons to 25 of its credit card holders. Their total credit card purchases over the next three months were compared to the credit card purchases over the next three months for 25 credit card holders who were not sent discount coupons. Determine whether the samples are dependent or independent. A) dependent B) independent
Answers
1. The two given samples are dependent.
2. The two samples are dependent.
Classify the two given samples as independent or dependent:
Sample 1: Pre-training weights of 19 people
Sample 2: Post-training weights of the same 19 people
Answer: A) Dependent
The two samples are dependent because they come from the same set of 19 people. The weights of individuals were measured before and after training, creating a paired relationship between the observations. Any change in weight can be directly attributed to the training, and the two measurements are not independent of each other.
Determine whether the samples are dependent or independent:
Sample 1: Credit card purchases over three months for 25 credit card holders who received discount coupons.
Sample 2: Credit card purchases over three months for 25 credit card holders who did not receive discount coupons.
Answer: A) Dependent
The two samples are dependent because they are based on the same group of credit card holders. The comparison is made between the credit card purchases of individuals who received discount coupons and those who did not. The presence or absence of discount coupons directly influences the purchasing behavior of each credit card holder. Therefore, the observations within each sample are not independent, making the samples dependent.
To know more about independent or dependent refer here:
https://brainly.com/question/14524222
#SPJ11
answer for points and brainiest!

Answers
Step-by-step explanation:
Yes
yes
yes
no
hope this helps
2(x+3)=x
16x+20=4(4x+5)
3(x+8)=3x+7
5(x+1)=10x+3
the x's are not the same in each rpoblem
Answers
The solutions for the linear equations are:
1) x = -6
2) infinite solutions.
3) no solutions.
4) x = 2/5
How to solve the linear equations?Here we have some linear equations that we need to solve, to do so, we just nee to isolate the variable x.
The first linear equation is:
2*(x +3) = x
2*x + 6 = x
2*x - x = -6
x = -6
That is the solution.
The next linear equation is:
16*x + 20 = 4*(4x + 5)
Expanding the right side:
16*x + 20 = 16*x + 20
We have the same thing in both sides, so we have infinite solutions.
The third one is:
3(x+8)=3x+7
Expanding the left side:
3x + 24 = 3x + 7
Subtracting 3x in both sides we get:
24 = 7
This is false, so this equation has no solutions.
The last one is:
5(x+1)=10x+3
Expanding the left side:
5x + 5 = 10x + 3
5 - 3 = 10x - 5x
2 = 5x
2/5 = x
That is the solution.
Learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
(z+4) (z+2) (z − 1) = 0
-
Select all of the following values that make the equation true.
04
01
0-4
00
0-2
02
0-1

Answers
The Zero Product Property simply notes that if ab = 0, then either a = 0 or b = 0. The solutions exists x = -4, x = -2, x = 1.
What is meant by zero-factor rule?The zero-product property in algebra asserts that two nonzero items cannot be multiplied together to produce zero.
The Zero Product Property simply notes that if ab = 0, then either a = 0 or b = 0 (or both). A product of factors exists zero if and only if one or more of the factors exists zero.
Let the given equation be (x+4)(x+2)(x-1)=0
By using the Zero Factor Principle, we get
If ab = 0 then a = 0 or b = 0
then x + 4 = 0 or x + 2 = 0 or x - 1 = 0
Solve x + 4 = 0
⇒ x = -4
Solve x + 2 = 0
⇒ x = -2
Solve x - 1 = 0
⇒ x = 1
The solutions are x = -4, x = -2, x = 1
Therefore, the correct options exists:
b) 1
c) -4
e) -2
The complete question is:
An equation is shown below.
(x + 4)(x + 2)(x - 1) = 0
Select all of the following values that make the equation true.
a) 4
b) 1
c) -4
d) 0
e) -2
f) 2
g) -1
To learn more about Zero Product Property refer to:
https://brainly.com/question/26899097
#SPJ13
A section of a tessellated plane is shown. Which type of symmetry does the tessellated plane have?
Answers
The supplied figure's half is tipped downward; therefore, to make them symmetric, we must translate the figure upwards. Anden consider the negative image.
what is symmetry?In mathematics, symmetry is the quality of an object being split into two identical, mirrored parts. What does axis of symmetry mean? The term "axis of symmetry" refers to a hypothetical line that can fold or divide an item into two identical mirror halves. If two halves can fit together, then anything is symmetrical. Drawing a mirror line in the center and making sure both halves are the same will allow you to determine the shape's symmetry. To put it another way, symmetry is when two things are facing one another or when two things have mating pieces that revolve about an axis.
The supplied figure's half is tipped downward; therefore, to make them symmetric, we must translate the figure upwards. Anden consider the negative image. We obtain the translational and reflective symmetry.
To know more about symmetry visit:
https://brainly.com/question/1597409
#SPJ1
Moya is moving to a new house and packing up. She has 70 kilograms of books and 127 kg kilograms of clothing to send through the postal service. How much more do her clothes weigh than her books? How much is her shipping cost of she has to pay $80 per kg of books and $200 per kg of clothing?
Answers
The difference in her clothes and her books will be 57kg.
The difference in shipping cost if she has to pay $80 per kg of books and $200 per kg of clothing will be $19800.
How to calculate the value?From the information, Maya has 70 kilograms of books and 127 kg kilograms of clothing to send through the postal service, the difference in her clothes and her books will be:
= Weight of clothes - Weight of books
= 127 kg - 70 kg
= 57 kg
The difference in shipping cost if she has to pay $80 per kg of books and $200 per kg of clothing will be:
= 127(200) - 70(80)
= 25400 - 5600
= $19800
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
What is the Domain and Range of the function f(x)\(\sqrt{x-7} +9\)?
Answers
For the given function, the domain is D : { x ≥ 7} and the range is R: { y ≥ 9}
How to get the domain and range?
Here we have a square root, remember that the argument of the square root must be equal or larger than zero, so the domain is such that:
x - 7 ≥ 0.
Solving for x we get:
x ≥ 0 + 7
Then the domain is:
x ≥ 7
To get the range, we evaluate in the minimum of the domain:
f(7) = √(7 - 7) + 9 = 9
Then the range is the set of all values larger than 9, because the function is increasing.
So the range is R: y ≥ 9.
If you want to learn more about domain and range:
https://brainly.com/question/10197594
#SPJ1
factor the expression using the gcf 25+50
Answers
Answer:
25(1+2)
Step-by-step explanation:
25 goes into 25 once and 50 twice.
Solve the equation, give the exact solution then approximate the solution to the nearest hundredth if necessary

Answers
We solve as follows:
\(\frac{x^2}{3}=49\Rightarrow x^2=147\)\(\Rightarrow\begin{cases}x=7\sqrt[]{3} \\ x=-7\sqrt[]{3}\end{cases}\)We have that the solutions for the problem are x = 7sqrt(3) or x = -7sqrt(3).
What is the slope-intercept equation for the linear function represented by the
table?

Answers
Answer: y= 3/2x - 6
Step-by-step explanation:
The equation is y=mx + b
The y-intercept is when x = 0, so on the table y-intercept = -6
The slope is rise/run, we see that y increase by three and x increase by 2, so the slope is 3/2
to get the slope of any straight line, we simply need two points off of it, let's use those ones in the picture below.
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{-3})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{3}-\stackrel{y1}{(-3)}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{2}}} \implies \cfrac{3 +3}{4} \implies \cfrac{ 6 }{ 4 } \implies {\Large \begin{array}{llll} \cfrac{3 }{ 2 } \end{array}}\)
now, the y-intercept occurs when x = 0, recheck the picture below.

I need serious help, this is hard

Answers
======================================================
Explanation:
M is the midpoint of segment PQ. This means PQ is cut in half into two equal smaller pieces PM and MQ. We can say that PM = MQ.
Furthermore, we can say that PQ is twice as long as either piece, so
PQ = 2*PMPQ = 2*MQWe'll use the second equation to say the following:
PQ = 2*MQ
6x+56 = 2*MQ .... replace PQ with 6x+56
6x+56 = 2*(5x+8) .... replace MQ with 5x+8
6x+56 = 2*5x + 2*8 .... distribute
6x+56 = 10x+16
6x+56-10x = 16 .... subtract 10x from both sides
-4x+56 = 16
-4x = 16-56 ..... subtract 56 from both sides
-4x = -40
x = -40/(-4) ..... divide both sides by -4
x = 10
Once we know the value of x, we use it to find the length of PM
PM = MQ
PM = 5x+8
PM = 5*10+8
PM = 50+8
PM = 58
Note how PQ = 6x+56 = 6*10+56 = 116 is exactly twice as large compared to 58. In other words, 2*58 = 116. This confirms that PQ is twice as long compared to PM or MQ. This helps confirm we have the right answer.
( PLEASE HELP IT HAS A TIMER ) What are the coordinates of point H?
-3,1 1/2
-1 1/2,3
1 1/2 , 3
3, -1 1/2

Answers
Answer:
-1 1/2, 3
Step-by-step explanation:
Which number is the BASE?
23=8
8
Answers
Answer:
Step-by-step explanation:
For example, the base-8 numeral 23-8 contains two digits, "2" and "3", and with a base number (subscripted) "8". When converted to base-10, the 23-8 is equivalent to 19-10, i.e. 23-8 = 19-10.
2. The function ln(x)2 is increasing. If we wish to estimate √ In (2) In(x) dx to within an accuracy of .01 using upper and lower sums for a uniform partition of the interval [1, e], so that S- S < 0.01, into how many subintervals must we partition [1, e]? (You may use the approximation e≈ 2.718.)
Answers
To estimate the integral √(ln(2)) ln(x) dx within an accuracy of 0.01 using upper and lower sums for a uniform partition of the interval [1, e], we need to divide the interval into at least n subintervals. The answer is obtained by finding the minimum value of n that satisfies the given accuracy condition.
We start by determining the interval [1, e], where e is approximately 2.718. The function ln(x)^2 is increasing, meaning that its values increase as x increases. To estimate the integral, we use upper and lower sums with a uniform partition. In this case, the width of each subinterval is (e - 1)/n, where n is the number of subintervals.
To find the minimum value of n that ensures the accuracy condition S - S < 0.01, we need to evaluate the difference between the upper sum (S) and the lower sum (S) for the given partition. The upper sum is the sum of the maximum values of the function within each subinterval, while the lower sum is the sum of the minimum values.
Since ln(x)^2 is increasing, the maximum value of ln(x)^2 within each subinterval occurs at the right endpoint. Therefore, the upper sum can be calculated as the sum of ln(e)^2, ln(e - (e - 1)/n)^2, ln(e - 2(e - 1)/n)^2, and so on, up to ln(e - (n - 1)(e - 1)/n)^2.
Similarly, the minimum value of ln(x)^2 within each subinterval occurs at the left endpoint. Therefore, the lower sum can be calculated as the sum of ln(1)^2, ln(1 + (e - 1)/n)^2, ln(1 + 2(e - 1)/n)^2, and so on, up to ln(1 + (n - 1)(e - 1)/n)^2.
We need to find the minimum value of n such that the difference between the upper sum and the lower sum is less than 0.01. This can be done by iteratively increasing the value of n until the condition is satisfied. Once the minimum value of n is determined, we have the required number of subintervals for the given accuracy.
Learn more about integral here : brainly.com/question/31059545
#SPJ11
Plz help I’m timed :(

Answers
Answer:
y=5/3x+5
Step-by-step explanation:
Answer:
y=3/5x+5
Step-by-step explanation:
slope: 6/10=3/5
y-intercept: 5
hopefully this helps :)
dose it matter when finding if a slope is positive or negative if the line goes through the origin?
Answers
A company had returns of 5%, 10%, -15%, 20%, -12%, 22%, 8% in
the last few years. Compute the arithmetic average return,
geometric average return, variance, and standard deviation of
returns.
Refer to
Answers
Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
Given, Returns of the company for the last few years are 5%, 10%, -15%, 20%, -12%, 22%, 8%
Arithmetic Average return:
Arithmetic Average return = (sum of all returns) / (total number of returns)
Arithmetic Average return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Therefore, the arithmetic average return of the company is 2.57%.
Geometric average return:
Geometric average return = [(1+R1) * (1+R2) * (1+R3) * …….. * (1+Rn)]1/n - 1
Geometric average return = [(1.05) * (1.1) * (0.85) * (1.2) * (0.88) * (1.22) * (1.08)]1/7 - 1= 0.13
Therefore, the geometric average return of the company is 13%.
Variance:
Variance = (sum of (return - mean return)2) / (total number of returns)
Mean return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Variance = [(5-2.57)2 + (10-2.57)2 + (-15-2.57)2 + (20-2.57)2 + (-12-2.57)2 + (22-2.57)2 + (8-2.57)2] / 7= 392.12 / 7= 56
Therefore, the variance of the company is 56.
Standard Deviation:
Standard Deviation = Square root of Variance
Standard Deviation = √56= 7.48
Therefore, the standard deviation of the company is 7.48%.
Thus, Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
To know more about arithmetic average return, click here
https://brainly.com/question/28562900
#SPJ11
Which equation best represents the relationship between x and y in the
graph?

Answers
The equation y + 2x = 3 best represents the relationship between x and y in the graph.
We are provided with the graph shown in question. We were supposed to find the equation of the line shown in the graph. From this graph we can clearly see that the line is passing through ( 1.5 , 0 ) and ( 0 , 3 ).
The equation of line passing through two points is given below:
\((y - y_{1}) = (\frac{y_{2}-y_{1} }{x_{2}-x_{1} }) (x - x_{1} )\)
As the line is passing through points ( 1.5 , 0 ) and ( 0 , 3 ) , so we can write the above equation as
( y - 0 ) = ( ( 3 - 0 )/( 0 - 1.5 ) ) ( x - 1.5 )
y = -2 ( x - 1.5 )
y = -2x + 3
y + 2x = 3
The required equation of line is y + 2x = 3 i.e., this equation best represents the relationship between x and y in the graph.
To know more about equation of line refer to the link:
https://brainly.com/question/18831322
#SPJ9