Answers
Answer: y = (x - 1)² - 3
Step-by-step explanation:
y = (1-1)²-3
y=0-3
y=-3
Related Questions
Find the root(s) of f (x) = (x- 6)2(x + 2)2. -6 with multiplicity 1 -6 with multiplicity 2 6 with multiplicity 1 6 with multiplicity 2 -2 with multiplicity 1 -2 with multiplicity 2 2 with multiplicity 1 2 with multiplicity 2 Find the root(s) of f (x) = (x + 5)3(x - 9)2(x + 1). -5 with multiplicity 3 5 with multiplicity 3 -9 with multiplicity 2 9 with multiplicity 2 -1 with multiplicity 0 -1 with multiplicity 1 1 with multiplicity 0 1 with multiplicity 1
Answers
The root(s) of f (x) are
6 with multiplicity 2
-2 with multiplicity 2.
What is the solution to an equation?
In order to make the equation's equality true, the unknown variables must be given values as a solution. In other words, the definition of a solution is a value or set of values (one for each unknown) that, when used as a replacement for the unknowns, transforms the equation into equality.
We are given to find the roots of the following polynomial function :
f (x) = (x- 6)²(x + 2)²
We know that
the roots of a polynomial f(x) are given by the equation f(x) = 0.
Therefore, the roots of the given polynomial are given by
(x- 6)² =0 => x =6,6
(x + 2)² =0 , x =-2, -2
Thus, the required roots are
6 with multiplicity 2 and -2 with multiplicity 2.
To learn more about the solution of an equation from the given link
https://brainly.com/question/22688504
#SPJ1
431.67 In a different number, the 4 represents a value which is one-tenth of the value of the 4 in the number above. What value is represented by the 4 in the other number?
Answers
So the different number has a 4 with a value of 40.
What is Algebraic expression ?
Algebraic expression can be defined as combination of variables and constants.
To solve this problem, we need to first identify the place value of the digit 4 in the given number.
The digit 4 is in the hundreds place in the number 431.67, so its value is 4 x 100 = 400.
According to the problem statement, the 4 in the different number represents a value which is one-tenth of the value of the 4 in 431.67. Therefore, the value of the 4 in the different number is:
400/10 = 40
To determine the value of the different number, we need to look at the other digits in the number. Since we don't have any information about the other digits, we cannot determine the value of the different number. The answer is that the value of the different number cannot be determined with the information given.
Therefore, So the different number has a 4 with a value of 40.
To learn more about Algebraic expression from given link.
brainly.com/question/28884894
#SPJ1
1. which expression is equivalent to 4(9+3).
Multiple Select three expressions
A. 4(12)
B. 36+3
C. 36+12
D. 4+(9+3)
E. (9+3) +(9+3) +(9+3) +(9+3)
Answers
Answer:
A. 4(12)
C. 36+12
E. (9+3) +(9+3) +(9+3) +(9+3)
Step-by-step explanation:
\(4(9+3)=48\)
\(4*9=36\\4*3=12\)
\(48\)
\(4*12=48\)
\(36+12=48\)
\((9+3) +(9+3) +(9+3) +(9+3)\\12+12+12+12\)
=48
PLS HELP BRAINLIEST AND 100 POINTS PLS HELP FOR ALL I WILL GIVE BRAINLIEST TYYYSMMM

Answers
Answer + Step-by-step explanation:
Check the illustration that I provided .

Please help ASAP! Thank you

Answers
Answer:
a. lines intersecting at a single point
b. one solution
Step-by-step explanation:
a. The equations can be rewritten as:
y = -5x+23 and y = -1/6x+1
Comparing the equations with standard equation: y=mx+c, where m is the gradient of the line formed by the linear equation.
Since the gradient of the lines are different then the lines cannot be parallel and will intersent at one point.
b. The equation will have one solution as below.
The equations can be rewritten as:
5x+y=23
5x+30y=30
Subtracting both equation will result in,
29y=7
=> y=7/29
Hence x= 660/29
Twenty years ago a small town in Texas had a population of 10,000. The population has increased 8% each year since then. What is the current population of this town?
Answers
Answer:
25,200
Step-by-step explanation:
Increase in population per year =8%=((100+8)*10,000)/100=10,800. So,there will be an increment of 800 people to the population every year. =>after twenty years,the total population=10,000+19*(800)=25,200.
Answer:
10800
Step-by-step explanation:
10000+8%=10800
hope this helps:)
please help it due rn

Answers
Answer:
B) (1/2, -8)
Step-by-step explanation:
(1, -6) and (0, -10)
Midpoint formula:
((x1+x2)/2, (y1+y2)/2)
Solving for x:
(x1+x2)/2
(1 + 0)/2
1/2
Solving for y:
(y1+y2)/2
(-6-10)/2
(-16)/2
-8
Find the area of a regular hexagon with an apothem 8.7 centimeters long and a side 10 centimeters long. Round your answer to the nearest tenth.
Answers
Answer:
Step-by-step explanation:
A regular hexagon is made up of six triangles having a height of 8.7cm and a base of 10cm. So the area of the hexagon is 6 times the area of one of the triangles. Since the area of a triangle is bh/2 we have
A=6(8.7)10/2
A=261cm^2
Answer:
261 cm²
Step-by-step explanation:
The area of the hexagon is 6 times the area of one of the triangles. The area of a triangle is base × height ÷ 2.
A = 6(8.7)10 ÷ 2
A = 261 cm²
60% of the books in a library are for adults, 5% are for young people and the rest are for children. If there are 280 books for children, how many books are there altogether?
Answers
Answer:
800 books
problem solving steps:
adults:60%
young people:5%
children=100%-60%-5%
=35%
35%=280 books
1%=280÷35
=8
100%=800
so,there are 800 books
Which operation should be done first in the
expression below?
(2 + 2) * 3 - 1-4
Answers
Answer:
7
Step-by-step explanation:
PEMDAS
First we do the parenthesis, then we multiply and then we subtract (left to right)
= (2+2) * 3 - 1 - 4
= 4 * 3 - 1 -4
= 12 - 1 -4
= 12
What is a inequality on a number line
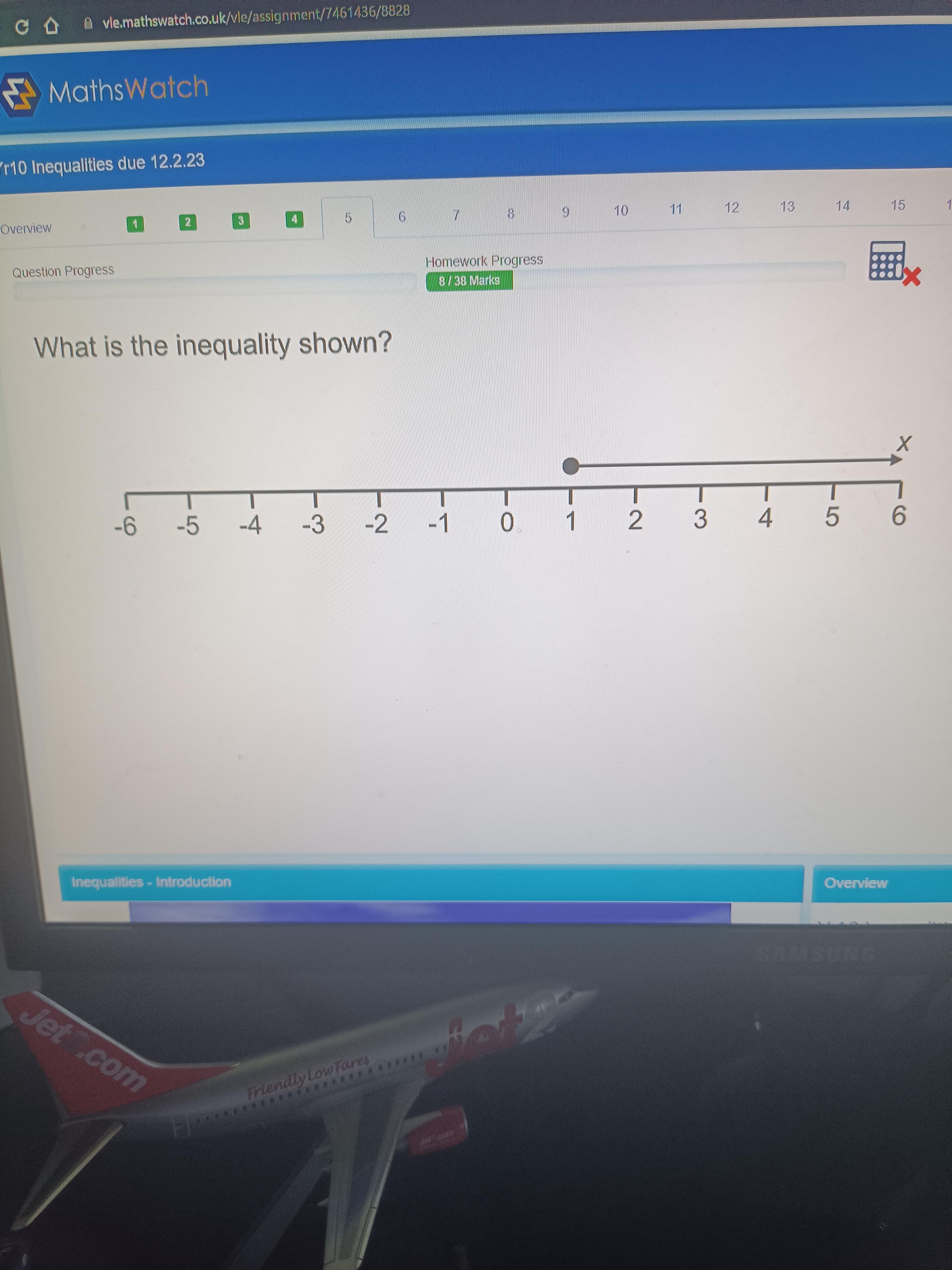
Answers
Answer:
add wtwo numbers x by 3? I am sorry don't understand question
Step-by-step explanation:
ANOTHA ONE LETS GOOOOOO

Answers
Answer:
1/560
Step-by-step explanation:
So the x input which is the top row the numbers increase by 1 so that is your top number of your slope (rate of change)
And your bottom row increases by 560 so that is your bottom number of your slope
So your rate of change is 1/560
How do I know where to get these numbers?
Well if you take the first 2 numbers from the top row (in your case 1 and 2) and subtract them from each other (2-1=1) you get your first number. Then you do the same for the bottom (in your case 560 and 1120) subtract them (1120-560=560) and get your bottom....If needed you can simplify your fraction but sometimes your slope can come out as a whole number instead of a fraction but in your case you have a fraction.
That is where you get 1/560
Hope this helped!
63.7+(-26) what is 63.7 plus negative 26
Answers
Answer: 63.7 + (-26) = 37.7
Please help I’m stuck on the last one
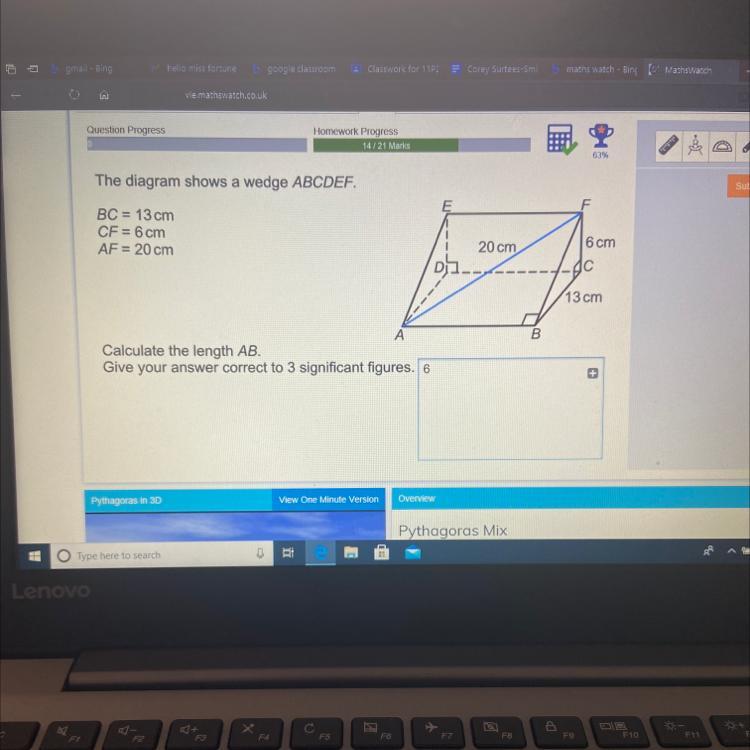
Answers
Answer:
AB = 14.0 cm
Step-by-step explanation:
Pythagora's Theorem
In a right triangle with a hypotenuse of length H and legs of lengths L and W, then it's satisfied the equation:
\(H^2 = L^2+W^2\)
The diagram shows a wedge ABCDEF and it's required to calculate the length of the side AB.
Note the triangle FCB is right at C, where side length is the hypotenuse:
\(BF^2=13^2+6^2\)
\(BF^2=169+36=205\)
Triangle ABF is right at B and 20 cm is the hypotenuse, thus:
\(20^2 =AB^2+BF^2\)
Solving for AB:
\(AB^2=20^2-BF^2\)
\(AB^2=20^2-205\)
\(AB^2=400-205=195\)
\(AB=\sqrt{195}\)
AB = 14.0 cm
Can somebody please help?? i’ll give Brainliest to whoever answers first.
There are 625 students in Leon's school. He takes a random sample of 75 students from the entire school population. In the sample, 33
students are planning to attend the end of year picnic.
Based on his data, how many students from the entire school are planning to attend the end of year picnic? Show ALL your work!
Answers
Answer:
The answer is 275 students.
Step-by-step explanation:
In 75 students, 33 students attend.
So the ratio is 33/75.
so multiply with 625.
625 x 33/75 = 275
Subtitute 2x+y=7 and 3x-y=8
Answers
Answer:
x = 3 , y = 1
Step-by-step explanation:
2x + y = 7
3x + y = 8
solution
2x + y = 7-----------(1)
3x - y = 8------------(2)
from equation 1
2x + y = 7
y = 7 - 2x-------------(3)
substitute equation 3 into equation 2
3x - y = 8
3x - (7 - 2x) = 8
3x - 7 + 2x = 8
3x + 2x = 8 + 7
5x = 15
divide through by the coefficient of x
5x/5 = 15/5
x = 3
to find y
substitute x into equation 1
2x + y = 7
2(3) + y = 7
6 + y = 7
y = 7 - 6
y = 1
You decide to clean the bathroom. You notice that the shower is covered in a strange green slime. You decide to try to get rid of this slime by adding lemon juice. You spray half of the shower with lemon juice and spray the other half of the shower with water. After 3 days of “treatment”, there is no change in the appearance of the green slime on either side of the shower.
Independent Variable:
Dependent Variable:
Control:
Constant:
Answers
A variable is defined as the alphabetic character that expresses the unknown value or unknown number. It can be changed according to the operations performed.
In this experiment,
Each side of the shower is sprayed with lemonade juice to determine whether it has any changes in the cleanliness of the shower. So each side of the shower with lemon juice is an independent variable.
This dependent variable is a variable that can measure Lemonade a manipulated variable or independent variable has any effect on it, such as whether lemonade juice cleans the slime off of the side or not.
A control is something that remains unchanged to assess the condition or impact which has not changed or may be contrasted to it. In the this scenario, the water spray is under command.
The experiment concludes drinking lemonade seems to not influence the cleaning of slime inside the shower.
Thus, slime is constant.
Hence,
Each side of the shower with lemon juice is an independent variable.Shower cleanliness is a dependent variable.A water spray can be used to keep things under control.Slime is constant.Learn more about variables here:
https://brainly.com/question/2466865
#SPJ9
i need help
can you look over this picture and see what the answer is

Answers
Answer:
AC = 12
Step-by-step explanation:
If BC is parallel to DE then ∠D ≅ ∠B and ∠E ≅ ∠C. Therefore
ΔABC is similar to ΔADE.
The sides of smaller triangle are in proportion with sides of bigger triangle.
Therefore we have the equation:
AC/AE = AB/AD
Substitute the given numbers:
x/x+15 =8/18
18x= 8(x+15)
18x = 8x+120
10x = 120
x = 12
AC=12
The graph of the invertible function f is shown on the grid below.
What is the value of f -1(6)?

Answers
We have been given graph of function \(y=f(x)\). We are asked to find the value of \(f^{-1}(6)\) from the graph of \(y=f(x)\).
We know that to find an inverse function is a function that reverses another function. A function f(x) gives an output of y, when we input some value of x. The inverse of f(x) will give the same value of x from value of y.
So to find inverse of a function we need to switch all x and y values.
We can see that \(f(4)=6\), so to to find value of \(f^{-1}(6)\), we have to switch x and y values.
After switching x and y values, we will get:
\(f^{-1}(6)=4\)
Therefore, \(f^{-1}(6)=4\).
Answer:
4
Step-by-step explanation:
Find the greatest common factor.14t^4, 18t^2Write your answer as a constant times a product of single variables raised to exponents.
Answers
To find the greatest common factor (GCF), I like to split it up into two steps:
1. Find the greatest common factor of the coefficients.
2. Find the greatest common factor of the variables and any exponents.
For starters, we will find the GCF of 14 and 18.
List the factors of 14:
1, 2, 7, 14
List the factors of 18:
1, 2, 3, 6, 9, 18
Now, find the factor that is the largest of the two: 2.
The GCF of 14 and 18 is 2.
Now, find the GCF of t² and t⁴.
Factors of t²: t, t²
Factors of t⁴: t, t², t⁴
The GCF of t² and t⁴ is t².
Now, put them together: 2t².
The GCF of 14t⁴ and 18t² is 2t².
A 500-kg concrete block 95 cm longcm wide and cm high. It can exert three different pressures on a horizontal surface depending on which faceit rests on the highest pressure is
Answers
Pressure is force per unit area. If the block is sitting at rest on the surface, it applies a pressure of mg/A, where mg is the block's weight and A is the area of the face that makes contact with the surface.
The smaller the value of A, the larger the pressure. So the highest pressure the block can exert is achieved when it's resting on the face with the smallest dimensions.
If the block is a cube with side length 95 cm, then the pressure exerted by each face is the same.
Sean burns 8.5 calories per minute when he runs. How many calories does he burn if he
runs for 45 minutes?
Answers
Answer:382.5
Step-by-step explanation: 45 x 8.5 = 382.5
Suppose that $2000 is invested at an interest rate of 4.75% per year, compounded continuously. After how many years will the initial investment be doubled?
Answers
Answer: it will take approximately 14.62 years for the initial investment to double at an interest rate of 4.75% per year, compounded continuously.
Step-by-step explanation: Given an investment of $2000 at a continuously compounded interest rate of 4.75%, the balance in the account can be calculated using the following mathematical expression after t years:
The aforementioned equation, A = P * e^(rt), denotes the relationship between the accrued amount (A) and the principal amount (P), compounded continuously at a fixed annual rate of interest (r) over a specific time period (t), as governed by the mathematical constant "e."
In the context of financial calculations, the symbol 'P' denotes the initial capital investment. The interest rate, represented by the variable 'r', is expressed in the form of a decimal. Additionally, 'e' is the mathematical constant, roughly equivalent to 2.71828. Finally, 't' refers to the duration of the investment, measured in years.
In order to determine the duration of time required for the investment to achieve a twofold increase, it is necessary to solve the corresponding equation:
The equation expressed as 2P = P * e^(rt) can be restated more formally as follows. Given a principal investment amount represented by P and a rate of return indicated by r, compounded over time t, the equation can be expressed as the product of P and the exponential function of e^(rt), yielding twice the initial investment amount.
The variable 2P represents the monetary value acquired through doubling the initial investment.
Upon division of both sides by P, the resulting expression is as follows:
The equation 2 equals the exponential function of the base e raised to the power of the product of r and t.
By applying the natural logarithm function to both expressions, the resultant outcome is:
The natural logarithm of 2 can be represented as rt, where r denotes the logarithmic base and t denotes the logarithm of the argument, in accordance with the conventions of academic mathematical writing.
Upon resolving for the variable t, an outcome is yielded:
The mathematical expression t = ln(2) / r can be written in a formal academic style as follows: The equation determines the relationship between time t and the rate of decay r, where t is equal to the natural logarithm of 2 divided by r.
Upon substitution of the provided values, the resultant output is:
The calculated value of the variable t, representing the length of time in years, is approximately equal to 14.62 years, obtained through the algebraic manipulation of the natural logarithmic function of 2 divided by the constant value of 0.0475.
Evaluate the double integral ∬R(3x−y)dA, where R is the region in the first quadrant enclosed by the circle x2+y2=16 and the lines x=0 and y=x, by changing to polar coordinates.
Answers
Answer:
\(\displaystyle 64-32\sqrt{2}+\frac{32\sqrt{2}}{3}\approx3.66\)
Step-by-step explanation:
\(\displaystyle \iint_R(3x-y)\,dA\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0(3r\cos\theta-r\sin\theta)\,r\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0(3r^2\cos\theta-r^2\sin\theta)\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\int^4_0r^2(3\cos\theta-\sin\theta)\,dr\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\frac{64}{3}(3\cos\theta-\sin\theta)\,d\theta\\\\=\int^\frac{\pi}{2}_\frac{\pi}{4}\biggr(64\cos\theta-\frac{64}{3}\sin\theta\biggr)\,d\theta\)
\(\displaystyle =\biggr(64\sin\theta+\frac{64}{3}\cos\theta\biggr)\biggr|^\frac{\pi}{2}_\frac{\pi}{4}\\\\=\biggr(64\sin\frac{\pi}{2}+\frac{64}{3}\cos\frac{\pi}{2}\biggr)-\biggr(64\sin\frac{\pi}{4}+\frac{64}{3}\cos\frac{\pi}{4}\biggr)\\\\=64-\biggr(64\cdot{\frac{\sqrt{2}}{2}}+\frac{64}{3}\cdot{\frac{\sqrt{2}}{2}}\biggr)\\\\=64-32\sqrt{2}+\frac{32\sqrt{2}}{3}\biggr\\\\\approx3.66\)
Week 2 4.0A.A.3 V 27 X 34
Answers
Answer:
is there a question for this problem if there is try your best
Select the correct answer.
What is the LCM of the numbers 3, 6, and 9?
A.
9
B.
18
C.
36
D.
54
Answers
Answer:
D
Because you have to find out what they could all equal up to
Answer:
d
Step-by-step explanation:
A passenger train is carrying 403 passengers in 13 cars. How many passenger are in each car?
Answers
Answer: 31 passengers are in each car.
Step-by-step explanation:
You divide:
403 ÷ 13 = 31
31 Passengers are in each chair.
I hope I helped you with this question. Have a great day!
Rearrange the parallelogram as a rectangle. Then find the area.
A drawing of a parallelogram on a grid. The figure has 2 and half unit squares along the length and 3 half squares along the width.

Answers
Answer:
9
Step-by-step explanation:
length*width
3*3=9
пожалуйста, помогите с векторами!

Answers
Answer:
hi there is that something you can block
Martin orders a pasta dish that is priced at $11.99. He also orders a drink. The total cost for the pasta and drink is $14.48. Which of the following equations can be used to find the cost of the drink?
Answers
Answer:
14.48=11.99+y
or
y=14.48-11.98
Step-by-step explanation:
it should be one of these (the variable might be different)
y is the price of the drink
