Derek is watching a thunderstorm. He hears the thunder 4.7 s after seeing a flash of lightning. How far away was the lightning?
Answers
Answer:
1.0014 Miles
Step-by-step explanation:
The light travels at 186,291 miles per second (~300,000 km/s), and speed of sound in dry air is equal to 0.21 - 0.22 miles per second (0.33-0.35 km/s), as it varies with the temperature. We can notice the lightning almost immediately even though the storm is far from us, but the thunder needs around 5 seconds to travel one mile and approximately 3 seconds to travel one kilometer. Thanks to this seven orders of magnitude difference in sound and light propagation, we can easily estimate the storm distance
Answer:
This explanation is not good, can you please break it down so we can see how you guys got this answer?
Step-by-step explanation:
Related Questions
Solve the following inequality.
8(x+5)≥0
x≤5
x≤−5
x≥−5
x≥5
Answers
Answer:
the third one
Step-by-step explanation:
8x + 40 ≥ 0
8x ≥ -40
x ≥ -5
I'm really confused about this question

Answers
Answer:
A. 10 ft
Step-by-step explanation:
Since dimensions of the wall are similar to the dimensions of the window.
Therefore, lengths and widths of wall and window would be in proportion.
So,
\( \frac{h}{2} = \frac{24.5}{4.9} \\ \\ h = \frac{24.5 \times 2}{4.9} \\ \\ h = \frac{49}{4.9} \\ \\ h = \frac{490}{49} \\ \\ h = 10 \: ft\)
When approximating S(x)dx using Romberg integration, R9,4 gives an approximation of order: h10 h8 h4 h6
Answers
R₄,₄ gives an approximation of order h⁸ when approximating ∫(a to b)f(x)dx using Romberg integration. Therefore second option is the correct answer.
When approximating the integral ∫(a to b) f(x) dx using Romberg integration, the term "R₄,₄" refers to the fourth row and fourth column of the Romberg matrix.
This specific entry represents the approximation obtained using the Romberg method with four iterations. The order of approximation is determined by the highest power of h in the error term of the approximation.
Since R₄,₄ has a subscript of 4, it indicates that the approximation is of order h⁸. This means that the error decreases at a rate of h⁸ as the step size h decreases, providing a more accurate estimation of the integral.
Therefore the correct answer is second option.
The question should be:
When approximating ∫(a to b)f(x)dx using Romberg integration, R₄,₄ gives an approximation of order:
h10
h8
h4
h6
To learn more about integration: https://brainly.com/question/988162
#SPJ11
A particular manufacturing design requires a shaft with a diameter of 21.000 mm, but shafts with diameters between 20.989 mm and 21.011 mm are acceptable. The manufacturing process yields shafts with diameters normally distributed, with a mean of 21.002 mm and a standard deviation of 0.005 mm. Complete parts (a) through (d) below. a. For this process, what is the proportion of shafts with a diameter between 20.989 mm and 21.000 mm? The proportion of shafts with diameter between 20.989 mm and 21.000 mm is (Round to four decimal places as needed.) . b. For this process, what is the probability that a shaft is acceptable? The probability that a shaft is acceptable is (Round to four decimal places as needed.) c. For this process, what is the diameter that will be exceeded by only 5% of the shafts? mm. The diameter that will be exceeded by only 5% of the shafts is (Round to four decimal places as needed.) d. What would be your answers to parts (a) through (c) if the standard deviation of the shaft diameters were 0.004 mm? . If the standard deviation is 0.004 mm, the proportion of shafts with diameter between 20.989 mm and 21.000 mm is (Round to four decimal places as needed.) T. If the standard deviation is 0.004 mm, the probability that a shaft is acceptable is (Round to four decimal places as needed.) mm. If the standard deviation is 0.004 mm, the diameter that will be exceeded by only 5% of the shafts is (Round to four decimal places as needed.)
Answers
In a manufacturing process, shaft diameters are normally distributed with a mean of 21.002 mm and a standard deviation of 0.005 mm. We need to calculate various probabilities and proportions related to shaft diameters.
a. To find the proportion of shafts with a diameter between 20.989 mm and 21.000 mm, we calculate the z-scores for these values using the formula: z = (x - μ) / σ, where x is the diameter, μ is the mean, and σ is the standard deviation. The z-score for 20.989 mm is z1 = (20.989 - 21.002) / 0.005, and for 21.000 mm, z2 = (21.000 - 21.002) / 0.005. We then use the z-scores to find the proportion using a standard normal distribution table or calculator. b. The probability that a shaft is acceptable corresponds to the proportion of shafts with diameters within the acceptable range of 20.989 mm to 21.011 mm. Similar to part (a), we calculate the z-scores for these values and find the proportion using the standard normal distribution.
c. To determine the diameter that will be exceeded by only 5% of the shafts, we need to find the z-score that corresponds to the cumulative probability of 0.95. Using the standard normal distribution table or calculator, we find the z-score and convert it back to the diameter using the formula: x = z * σ + μ.
d. If the standard deviation of the shaft diameters were 0.004 mm, we repeat the calculations in parts (a), (b), and (c) using the updated standard deviation value. By performing these calculations, we can obtain the requested proportions, probabilities, and diameters for the given manufacturing process.
To learn more about shaft diameters click here : brainly.com/question/31731971
#SPJ11
does this method require a parameter? if so, what type of parameter is required? what happens if you pass a different type of parameter instead? (try it
Answers
The type parameters act as placeholders for the types of the arguments passed to a method. The type parameter names throughout the method declaration must match those declared in the type parameter list.
Pass an array as a pointer to pass it as a parameter to a function (since it is a pointer). For instance, the following method sets array A's first n cells to 0.
In C++, an entire array cannot be provided as an argument. However, by mentioning the array's name, you can supply a pointer to an array without an index.
Only the array name is supplied as a parameter to pass a full array to a function. calculateSum(num), result But take note of how [] is used in the function specification. This tells the compiler that you are handing the function a one-dimensional array.
When we provide an array to a function as an argument, we are actually passing the address of the array in memory, which is the reference. To pass an array to a function, simply pass the array as the function's parameter (like normal variables).
Know more about parameter here:
brainly.com/question/19570024
#SPJ4
if you are given a box with sides of 7 inches, 9 inches, and 13 inches, what would its volume be?
Answers
To calculate the volume of a rectangular box, you multiply the lengths of its sides.
In this case, the given box has sides measuring 7 inches, 9 inches, and 13 inches. Therefore, the volume can be calculated as:
Volume = Length × Width × Height
Volume = 7 inches × 9 inches × 13 inches
Volume = 819 cubic inches
So, the volume of the given box is 819 cubic inches. The formula for volume takes into account the three dimensions of the box (length, width, and height), and multiplying them together gives us the total amount of space contained within the box.
In this case, the box has a volume of 819 cubic inches, representing the amount of three-dimensional space it occupies.
Learn more about Cubic Formula here :
https://brainly.com/question/27377982
#SPJ11
the angle θ is 7.2 degrees, and the circle arc s is 800 km. knowing that there are 360 degrees in a full circle what is the circumference of the surface of the earth? round to the closest 10,000 km. please explain how you came about your final solution.
Answers
The earth is 40000 kilometers around. There is no need to round off because the circumference already contains significant figures.
How do I calculate a circle's circumference?
A circle's diameter is multiplied by to determine its circumference (pi). You can also determine the circumference by multiplying 2radius by pi (=3.14).
Given: theta angle (central) = 7.2°; arc length S = 800 km
This indicates that an 800 km long arc is extending a circle with a 7.2° center angle ( earth in this case).
By definition, "An arc's length is a portion of a circle's diameter."
Therefore, we must first establish what percentage of the circle the specified arc length represents.
360° is a complete circle.
Thus, the fraction equals 7.2°/360°, or 1/50.
As a result, the stated arc length (800km) with a 7.2° central angle is 1/50th of the entire circle.
Thus, the whole circumference is 800 x 50, or 40000 km.
Alternately, you can calculate circumference using the formula below:
360° center angle x arc length as the circumference (theta)
Values substituted: circumference 800 = 360° 7.2°
circumference = 360°, 800°, and 7.2°, or 40000 kilometers
Therefore, the earth is 40000 kilometers around. There is no need to round off because the circumference already contains significant figures.
Learn more about Circumference
https://brainly.com/question/27447563
#SPJ4

I tried asking my teacher for help but this all she gave me. Please help I tried already and got it wrong. I am fine with just the answer or guessing because I already got it wrong so I get no credit now even if I get it right. But I still need to answer it to move on.
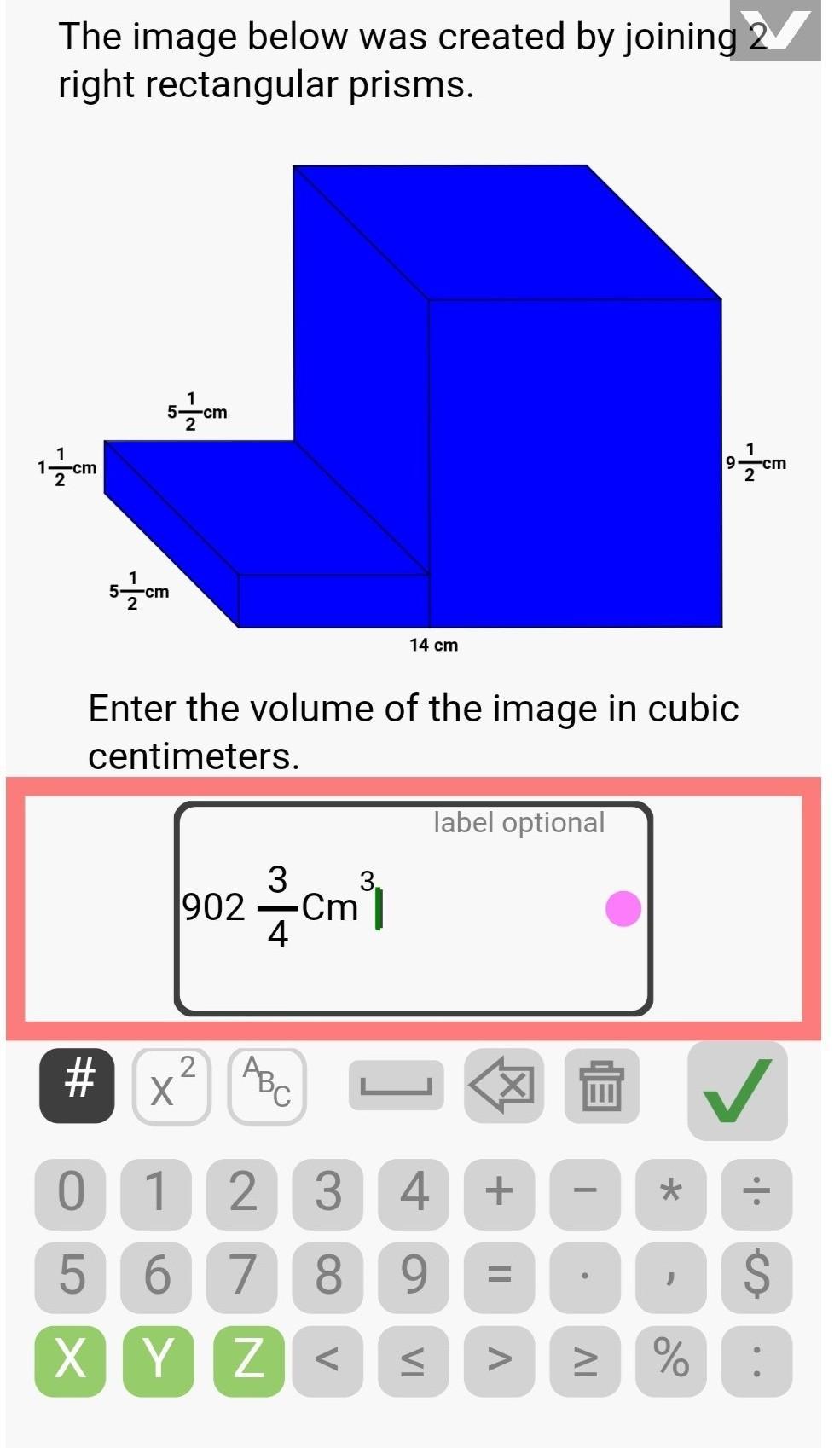
Answers
Answer:
489 1/2 cm
Step-by-step explanation:
So, the best first step is to break the complex shape into two smaller ones. I suggest breaking it down into 5 1/2 x 1 1/2 x 5 1/2 ( the smaller shape) and 9 1/2 x 5 1/2 x 8 1/2 (I got 8 1/2 but subtracting 5 1/2 from 14, I can elaborate if you need to). After that, just multiply and add. The first shape gives you 45 3/8. The second shape gets you 444 1/8. If you add them together, they give you 489 4/8 cm, simplified 489 1/2 cm.
(Tell me if this is incorrect)
Hope this helps!
Prove this identify : 2 cos^2 (45°-A ) = 1 +sin 2 A
Answers
According to a double angle identity, 2cos2θ - 1 = cos(2θ)
So, 2cos2(45° - x) - 1 = cos (90° - 2x)
= cos90°cos2x + sin90°sin2x
= (0)cos2x + (1)sin2x
= sin2x
Thus, 2cos2(45° - x) = 1 + sin2x
Questions:
1) What is the length of AB, written in simplest radical form?
2) What is the perimeter of the triangle?
SHOW FULL WORK PLEASE

Answers
In the given triangle, the length of AB is 3√3 units
The perimeter is 2√5 + √7 + 3√3 units
Calculating the perimeter of a triangleFrom the question, we are to determine the length of AB and then calculate the perimeter of the triangle
To determine the length of AB, we will use the Pythagorean theorem
We can write that
AB² = AC² + BC²
AB² = (2√5)² + (√7)²
AB² = 20 + 7
AB² = 27
AB = √27
AB = 3√3
The length of AB is 3√3 units
To calculate the perimeter, we will sum the length of all sides of the triangle
Perimeter of the triangle = 2√5 + √7 + 3√3 units
Hence, the perimeter is 2√5 + √7 + 3√3 units
Learn more on Calculating the perimeter of a triangle here: https://brainly.com/question/29244577
#SPJ1
Describe the transformation from the graph (Desmos!)

Answers
Answer: (I am really not sure the answer if it is wrong I am so sorry)
h=3, k=2
Horizontal: up, 2 units
Vertical: up, 3 units
In Mr. Senter's classroom, 2/3 of the students play sudoku. Of the students who play sudoku, 3/8 also play chess. If there are 24 students in his class, how many play sudoku and chess?
Answers
Answer:
9 students play sodoku and chess.
Step-by-step explanation:
What do we have?
2/3; play sudoku
3/8; play chess
24; students total
Find a common denominator for the fractions:
2/3x8/8
3/8x3/3
Now we have:
16/24
9/24
This also makes sense because we have a total of 24 students, now we want to know how many of them play sodoku AND chess; which was originally 3/8.
It's 9 students!
There are 16 students playing chess and 6 students playing sudoku.
What is the fraction?A fraction is defined as a numerical representation of a part of a whole that represents a rational number.
Given that 2/3 of the students play sudoku. of the students who play sudoku, 3/8 also play chess.
And there are 24 students in his class
First, we must determine how many students play chess, which is: In this scenario, we must multiply the total number of students by fractions to reach the answer.
⇒ 2/3×24 = 16
So 16 students are playing chess, and now, 3/8 of them are playing sudoku.
⇒ 3/8×16 = 6
Hence, there are 16 students playing chess and 6 students playing sudoku.
Learn more about the fraction here:
brainly.com/question/10354322
#SPJ2
Evaluate lim x->1 1/x^2-1 (Use a graph - show the graph and work the details
Answers
The limit of the function as x approaches 1 does not exist, since the function becomes infinitely large as x approaches 1 from both sides.
To evaluate the limit, we can start by analyzing the behavior of the function as x approaches 1 from both sides of the limit. We can also use a graph to visualize the function and see how it behaves near x = 1.
Here is a graph of the function f(x) = 1/(x^2 - 1):
Graph of f(x) = 1/(x^2 - 1)
As we can see from the graph, the function has vertical asymptotes at x = -1 and x = 1. This means that as x approaches 1 from both sides, the function becomes infinitely large.
To confirm this, let's evaluate the limit using algebraic manipulation:
lim x->1 1/(x^2 - 1)
= lim x->1 (1/((x-1)(x+1)))
= ∞
Therefore, the limit of the function as x approaches 1 does not exist, since the function becomes infinitely large as x approaches 1 from both sides.
Learn more about function from
https://brainly.com/question/11624077
#SPJ11
Find the height of the triangle by applying formulas for the area of a triangle and your knowledge about
triangles.
9 in
9 in.
Xin
6 in

Answers
Answer:
8.5
Step-by-step explanation:
Applying pythagora's theorem,
hypotenuse^2 = opposite^2 + adjacent^2
but, hypotenuse = 9
opposite = X
adjacent = 1/2(base of triangle)= 1/2(6)
adjacent = 3
9^2 = X^2 + 3^2
X^2 = 81 - 9
X^2 = 72
X = 8.5
PLEASE HELP ITS DUE AT nov 17 at 11:59

Answers
Two angles form a linear pair. The measure of one angle is z and the measure of the other angle is 2.4 times z plus 10°. Find the measure of each angle.
Answers
Two angles form a linear pair.
so, the sum of the angles are 180
the measure of the angles are z and (2.4 * z + 10)
so,
z + (2.4 * z + 10) = 180
solve for z
so,
z + 2.4 * z + 10 = 180
3.4 z = 180 - 10
3.4 * z = 170
divide both sides by 3.4
so, z = 170/3.4 = 50
so, the angles are 50 and 130
. A scale factor of 2 is applied to the dimensions of the prism. What effect will this have on the volume
Answers
The volume of the prism would be enlarged by a factor of 8
How to determine the effect?The scale factor is given as:
k = 2
Let the initial volume be v and the final volume be V.
The relationship between both volumes is
V = k^3 * v
This gives
V = 2^3 * v
Evaluate
V = 8v
Hence, the volume of the prism would be enlarged by a factor of 8
Read more about dilation at:
https://brainly.com/question/3457976
#SPJ1
Can somebody help me with this question. Will mark brainliest.

Answers
Answer:
4ft
Step-by-step explanation:
sorry for my mistake
Answer:
4 ft
Step-by-step explanation:
the ratios are as follows
X/6=50/75
50(6)=X(75)
300=75X
X=4
#10 Find three consecutive positive integers such that
the square of the first, increased by the fast, is 22
Answers
Solving a quadratic equation we can see that the 3 consecutive numbers are:
4, 5, and 6.
How to find the 3 consecutive integers?First, we can write 3 consecutive integers as:
x, (x + 1), and (x +2 )
The square of the first increased by the last is 22, then we can write:
x^2 + (x + 2) = 22
x^2 + x + 2 - 22 = 0
x^2 +x - 20 = 0
Using the quadratic formula we will get the solutions:
\(x = \frac{-1 \pm \sqrt{1^2 - 4*1*-20} }{2} \\\\x = \frac{-1 \pm 9}{2}\)
We know that x is positive, then the solution is:
x = (-1 + 9)/2 = 4
The 3 consecutive numbers are:
4, 5, and 6.
Learn more about quadratic equations at:
https://brainly.com/question/1214333
#SPJ1
URGENT
Look at △STU on this coordinate grid. Suppose that △S'T'U' is the result of a dilation of △STU with a scale factor of 2. What are the coordinates of point S'? *

Answers
Answer:
(4,2)
Step-by-step explanation:
THIS IS ASSUMING you are scaling it around 0,0
S is 2,1.
(x',y') = (2,1)
You want to find the coords with a scale factor of 2.
(x',y') = 2(2,1)
x',y' = 4,2
(4,2)
Here are the ingredients needed to make 8 pancakes.
Jacob makes 24 pancakes, work out how much milk he needs

Answers
Answer:
900 ml of milk
Step-by-step explanation:
the scale is 1:1 so just multiply by 3
For a two-dimensional potential flow, the potential is given by 1 r (x, y) = x (1 + arctan x² + (1+ y)², 2πT where the parameter A is a real number. 1+y x Hint: d arctan(x) dx 1 x² +1 (1) Determine the expression of the velocity components ux and uy. (2) Determine the value of I such that the point (x, y) = (0,0) is a stagnation point. (3) Assuming for the far field, the pressure and constant density are P. and p, respectively, determine the pressure at the point (0, -2). (4) The flow field corresponds to a flow around a cylinder. (Hint: Stream function is needed.) (a) Determine the centre and radius of the cylinder. (b) Determine the magnitude and direction of the resulting forcing acting on the cylind
Answers
For a two-dimensional potential flow, the potential is given by 1 r (x, y) = x (1 + arctan x² + (1+ y)², 2πT where the parameter A is a real number. Given potential function is;ϕ(x,y) = x(1 + arctan(x² + (1+y)²))/2πT
To find velocity components ux and uy, we need to take partial derivative of potential functionϕ(x,y) = x(1 + arctan(x² + (1+y)²))/2πTUsing the chain rule; ∂ϕ/∂x = ∂ϕ/∂r * ∂r/∂x + ∂ϕ/∂θ * ∂θ/∂x = cosθ * (1/r) * x(1+arctan(x² + (1+y)²))/2πT - sinθ * (1/r) * x(1+arctan(x² + (1+y)²))/2πT ∂ϕ/∂y = ∂ϕ/∂r * ∂r/∂y + ∂ϕ/∂θ * ∂θ/∂y = cosθ * (1/r) * x(1+arctan(x² + (1+y)²))/2πT - sinθ * (1/r) * x(1+arctan(x² + (1+y)²))/2πTNow, replace cosθ and sinθ with x/r and y/r respectively∂ϕ/∂x = x/(x²+y²) * x(1+arctan(x² + (1+y)²))/2πT- y/(x²+y²) * x(1+arctan(x² + (1+y)²))/2πT= [x²-y²]/(x²+y²) * x(1+arctan(x² + (1+y)²))/2πT∂ϕ/∂y = y/(x²+y²) * x(1+arctan(x² + (1+y)²))/2πT + x/(x²+y²) * x(1+arctan(x² + (1+y)²))/2πT= [2xy]/(x²+y²) * x(1+arctan(x² + (1+y)²))/2πT(2) To find stagnation point, we have to find (x,y) such that ux = uy = 0 and ϕ(x,y) is finite. Here, from (1) we get two equations; x(1+arctan(x² + (1+y)²))/2πT= 0 and x(1+arctan(x² + (1+y)²))/2πT + y(1+arctan(x² + (1+y)²))/2πT= 0For (1), either x=0 or arctan(x² + (1+y)²) = -1, but arctan(x² + (1+y)²) can't be negative so x=0. Thus, we get the condition y= -1 from (2)So, stagnation point is (0, -1).(3) For the far field, pressure is p, density is P. In potential flow, we have; P = ρv²/2 + P0, where P0 is constant pressure. Here, P0 = P and v = ∇ϕ so, P = ρ[ (∂ϕ/∂x)² + (∂ϕ/∂y)² ]/2Using expressions of ∂ϕ/∂x and ∂ϕ/∂y obtained above, we can find pressure at (0,-2).(4) Given flow is around a cylinder. For flow around cylinder, stream function can be written as; ψ(r,θ) = Ur sinθ (1-a²/r²)sinθTo find centre and radius of the cylinder, we find point where velocity is zero. We know that ψ is constant along any streamline. So, at the boundary of cylinder, ψ = ψ0, and at the centre of the cylinder, r=0.Using stream function, it is easy to show that ψ0= 0.So, at boundary of cylinder; U(1-a²/R²) = 0, where R is radius of cylinder, which gives R=aSimilarly, at centre; U=0To find the resulting force on the cylinder, we first have to find the lift and drag coefficients; C_d = 2∫_0^π sin²θ dθ = π/2 and C_l = 2∫_0^π sinθ cosθ dθ = 0We know that C_d = F_d/(1/2 ρ U²L) and C_l = F_l/(1/2 ρ U²L)where L is length of cylinder.So, F_d = π/2 (1/2 ρ U²L) and F_l= 0. Thus, the resulting force is F= (π/2) (1/2 ρ U²L) at an angle 90° to the flow direction.
To know more about dimensional, visit:
https://brainly.com/question/14481294
#SPJ11
Using these values, we can write Bernoulli's equation as: P + 1/2 * ρ * ((1 + arctan(5))^2 + (4/3)^2) = P_far
P = P_far - 1/2 * ρ * ((1 + arctan(5))^2 + (4/3)^2)
(1) To determine the expression for the velocity components ux and uy, we can use the relationship between velocity and potential in potential flow:
ux = ∂Φ/∂x
uy = ∂Φ/∂y
Taking the partial derivatives of the potential function Φ(x, y) with respect to x and y:
∂Φ/∂x = (1+arctan(x^2+(1+y)^2)) - x * (1/(1+x^2+(1+y)^2)) * (2x)
∂Φ/∂y = -x * (1/(1+x^2+(1+y)^2)) * 2(1+y)
Simplifying these expressions, we have:
ux = 1 + arctan(x^2+(1+y)^2) - 2x^2 / (1+x^2+(1+y)^2)
uy = -2xy / (1+x^2+(1+y)^2)
(2) To find the value of A such that the point (x, y) = (0,0) is a stagnation point, we need to find the conditions where both velocity components ux and uy are zero at that point. By substituting (x, y) = (0,0) into the expressions for ux and uy:
ux = 1 + arctan(0^2+(1+0)^2) - 2(0)^2 / (1+0^2+(1+0)^2) = 1 + arctan(1) - 0 = 1 + π/4
uy = -2(0)(0) / (1+0^2+(1+0)^2) = 0
For the point (x, y) = (0,0) to be a stagnation point, ux and uy must both be zero. Therefore, A must be chosen such that:
1 + π/4 = 0
A = -π/4
(3) To determine the pressure at the point (0, -2), we can use Bernoulli's equation for potential flow:
P + 1/2 * ρ * (ux^2 + uy^2) = constant
At the far field, where the velocity is assumed to be zero, the pressure is constant. Let's denote this constant pressure as P_far.
At the point (0, -2), the velocity components ux and uy are:
ux = 1 + arctan(0^2+(1-2)^2) - 2(0)^2 / (1+0^2+(1-2)^2) = 1 + arctan(5) - 0 = 1 + arctan(5)
uy = -2(0)(-2) / (1+0^2+(1-2)^2) = 4 / 3
Using these values, we can write Bernoulli's equation as:
P + 1/2 * ρ * ((1 + arctan(5))^2 + (4/3)^2) = P_far
Solving for P at the point (0, -2), we have:
P = P_far - 1/2 * ρ * ((1 + arctan(5))^2 + (4/3)^2)
To know more about potential function, visit:
https://brainly.com/question/30098140
#SPJ11
The degree of freedom to test if the coefficients on BDR and Age are statistically different from zero at the 5% level is The critical value for the preceding test using the Fm,wo distribution lable is (Enter your values exactly as they appear in the table ) The Fstatistic for omitting BDR and Age from the regression is F = 0.08. Are the coefficients on BDR and Age statistically different from zero at the 5% level? 0 A_ Because 0.08 is greater than the critica value the coefficients are jointly significant at the 5% level: Because 0.08 is less than the critical value, Ihe coefficients are jqintly significant at the 5% level: Because 0.08 less than the critical value, the coefficients are not jointly significant at the 59 level: Because 0.08 is greater Ihan the critical value the coefficients are not jointly significant at the 5% level.
Answers
This is because the F-statistic for omitting BDR and Age from the regression is 0.08, which is less than the critical value for the test using the F-distribution table.
To test if the coefficients on BDR and Age are statistically different from zero, we compare the F-statistic with the critical value from the F-distribution table. The F-statistic is a measure of the overall significance of the regression model when certain variables are omitted.
In this case, the F-statistic is given as 0.08. To determine if the coefficients are statistically different from zero at the 5% level, we compare this value with the critical value from the F-distribution table. The critical value represents the threshold beyond which we reject the null hypothesis.
Based on the statement provided, it states that 0.08 is "less than the critical value." Since the F-statistic is smaller than the critical value, we can conclude that the coefficients on BDR and Age are not jointly significant at the 5% level. In other words, we fail to reject the null hypothesis that the coefficients are equal to zero.
The use of the phrase "jointly significant" implies that the significance of the coefficients is considered together, rather than individually. The test assesses the overall impact of BDR and Age on the regression model, rather than their individual effects. Since the F-statistic falls below the critical value, we do not have sufficient evidence to conclude that BDR and Age have a significant impact on the model.
Learn more about Coefficients on BDR: brainly.com/question/32273904
#SPJ11
Find an equation for the plane consisting of all points that are equidistant from the points (1,0,-2) and (3,4,0).
Answers
The midpoint formula and the normal vector of the plane can be used to determine the equation of the plane that contains all points equidistant from the points (1,0,-2) and (3,4,0).
How is this determined?Given by: The midpoint of the two points is:
M = [(1 + 3)/2, (0 + 4)/2, (-2 + 0)/2] = (2, 2, -1) (2, 2, -1)
The following vector runs between the two points:
V = (3 - 1, 4 - 0, 0 - (-2)) = (2, 4, 2) (2, 4, 2)
The cross product of two non-parallel plane vectors yields the normal vector to the plane. The midpoint M to a point on the plane is one such vector, while the other is the vector V. Consider the point P = (2, 2, -1) + t(2, 4, 2) as an illustration, where t is a scalar.
The normal vector is then provided by:
N = V x (P - M) = (2, 4, 2) x (2t, 4t, 2t -1), which equals (12t, -8t, 4t + 2)
The point-normal form, which makes use of the normal vector N and the point M, can be used to determine the equation for the plane:
(x - 2) * 12t = (y - 2) * -8t = (z + 1) * 4t + 2
The final equation of the plane is obtained by multiplying both sides of the equation by t and setting t 0.
12(x - 2) = -8(y - 2) = 4(z + 1) + 2
Learn more about Coordinate geometry here:
brainly.com/question/18269861
#SPJ4
Find the regression equation, letting the first variable be the predictor (x) variable. Using the listed lemon/crash data, where lemon imports are in metric tons and the fatality rates are per 100,000 people, find the best-predicted crash fatality rate for a year in which there are 425 metric tons of lemon imports. Is the prediction worthwhile?
Lemon Imports Crash Fatality Rate
232 16
268 15.7
361 15.4
472 15.5
535 15
Answers
The regression analysis evaluates the amount of relationship that exists
between the variables in the analysis.
The regression equation is; \(\underline{\overline y = -0.00255 \cdot \overline x + 16.47268}\)The prediction is worthwhile because it gives an idea of the observed Crash Fatality Rate and it is therefore approximately correct.Reasons:
First part;
The given data is presented as follows;
\(\begin{tabular}{|cc|c|}Lemon Imports (x) &&Crash Fatality Rate\\232&&16\\268&&15.7\\361&&15.4\\472&&15.5\\535&&15\end{array}\right]\)
The least squares regression equation is; \(\overline y = b \cdot \overline x + c\)
Where;
\(b = \mathbf{\dfrac{\sum \left(x_i - \bar x\right) \times \left(y_i - \bar y\right) }{\sum \left(x_i - \bar x\right )^2 }}\)
\(\overline y\) = The mean crash fatality = 15.52
\(\overline x\) = The mean lemon import = 373.6
Therefore;
\(b = \dfrac{-171.36 }{67093.2 } = -0.00255\)
c = \(\overline y\) - b·\(\overline x\) = 15.52 - (-0.00255)×373.6 = 16.47268
Therefore;
The regression equation is \(\underline{\overline y = -0.00255 \cdot \overline x + 16.47268}\)Second part;
When the imports is 425 metric tons of lemon, we have;
\(\overline y\) = -0.00255 × 425 + 16.47268 = 15.38893 ≈ 15.4
Therefore;
When the import is 425 metric tons, the Crash Fatality Rate ≈ 15.4
Given that the predicted value is between the values for 268 and 535, we
have that the prediction is approximately correct or worthwhile
The prediction is worthwhile
Learn more about regression equation here:
https://brainly.com/question/5586207
A new car is purchased for \$49,000$49,000 and over time its value depreciates by one half every 5 years. What is the value of the car 11 years after it was purchased, to the nearest hundred dollars?
Answers
Set it up like 49000(1-0.05)^11
In ΔFGH, h = 40 cm, ∠H=17° and ∠F=84°. Find the length of g, to the nearest 10th of a centimeter.
Answers
In the given triangle, the length of g, to the nearest 10th of a centimeter is 134.3 cm
Calculating the length of the side of a triangleFrom the question, we are to determine the length of side g in the given triangle.
From the given information,
We have triangle FGH
From the law of sines, we can write that
g/sinG = h/sinH
From the given information,
h = 40 cm
∠H = 17°
and ∠F = 84°
Therefore,
∠H + ∠G + ∠F = 180° (Sum of angles in a triangle)
17° + ∠G + 84° = 180°
∠G + 101° = 180°
∠G = 180° - 101°
∠G = 79°
Thus,
g/sinG = h/sinH
g/sin79° = 40/sin17°
g = (40×sin79°)/sin17°
g = 134.3 cm
Hence, the length is 134.3 cm
Learn more on Calculating the length of a side of a triangle here: https://brainly.com/question/28061648
#SPJ1
find the perimeter of a quadrilateral with vertices at c (−2, 1), d (2, 4), e (5, 0), and f (1, −3).
Answers
A quadrilateral is a polygon with four sides. It is a two-dimensional shape formed by connecting four non-collinear points. The perimeter of the quadrilateral is 20 units.
The angles of a quadrilateral can vary, and it can have sides of different lengths. Examples of quadrilaterals include squares, rectangles, parallelograms, trapezoids, and rhombuses.
Quadrilaterals have certain properties and characteristics. Some common properties include:
Interior angles: The sum of the interior angles of a quadrilateral is always equal to 360 degrees.
Diagonals: A quadrilateral has two diagonals, which are line segments connecting opposite vertices. The diagonals of some quadrilaterals are perpendicular, while in others they intersect at a point inside the shape.
To find the perimeter of a quadrilateral with vertices at c (-2, 1), d (2, 4), e (5, 0), and f (1, -3), you can use the distance formula. The distance formula is given by:
d = √((x2 - x1)² + (y2 - y1)² )
So, let's calculate the distances between the vertices:
Distance between c and d:
d_cd = √((2 - (-2))² + (4 - 1)² )
Distance between d and e:
d_de = √((5 - 2)² + (0 - 4)² )
Distance between e and f:
d_ef = √((1 - 5)² + (-3 - 0)² )
Distance between f and c:
d_cf = √((-2 - 1)² + (1 - (-3))² )
Now, we sum the lengths of all four sides to find the perimeter:
Perimeter = CD + DE + EF + FC = 5 + 5 + 5 + 5 = 20
Therefore, the perimeter of the quadrilateral is 20 units.
To know more about perimeter visit:
https://brainly.com/question/9145366
#SPJ11
very fast
Show, by induction, that \( T(n)=10 n^{2}-3 n \quad \) if \( n=1 \)
Answers
Given that \(\(T(n)\) = \(10n^2-3n\)\) if (\(\(n=1\)\)), you have to prove it by induction. So, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if ( n= 1). The given statement is true for all positive integers n
Let's do it below: The base case (n=1) is given as follows: \(T(1)\) =\(10\cdot 1^2-3\cdot 1\\&\)=\(7\end{aligned}$$\). This implies that \(\(T(1)\)\) holds true for the base case.
Now, let's assume that \(\(T(k)=10k^2-3k\)\) holds true for some arbitrary \(\(k\geq 1\).\)
Thus, for n=k+1, T(k+1) = \(10(k+1)^2-3(k+1)\\&\) = \(10(k^2+2k+1)-3k-3\\&\)=\(10k^2+20k+7k+7\\&\) = \(10k^2-3k+20k+7k+7\\&\) = \(T(k)+23k+7\\&\) = \((10k^2-3k)+23k+7\\&\) = \(10(k+1)^2-3(k+1)\).
Therefore, we have proved that the statement holds true for n=k+1 as well. Hence, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if (n=1). Therefore, the given statement is true for all positive integers n.
For more questions on: integers
https://brainly.com/question/17695139
#SPJ8
a five-number summary for a data set is 35, 50, 60, 70, 90. about what percent of the observations are between 35 and 90?
Answers
Answer:
100%------------------
35 and 90 are the minimum and maximum values of the data set.
It means all observations are between those two numbers.
Hence the answer is 100%
Approximately 100% of the observations are between 35 and 90 in the given data set.
What is a median?
In statistics, the median is a measure of central tendency that represents the middle value of a set of data when arranged in ascending or descending order. It divides the data into two equal halves, with 50% of the values falling below the median and 50% falling above it.
To find the median, the data set is first arranged in order from smallest to largest (or vice versa). If the data set has an odd number of observations, the median is the middle value. For example, in a set of {1, 3, 5, 7, 9}, the median is 5.
The five-number summary consists of the minimum value, the first quartile (Q1), the median (Q2), the third quartile (Q3), and the maximum value. In this case, the minimum value is 35, and the maximum value is 90. Since these values define the range of the data set, all the observations are between these two values.
Therefore, approximately 100% of the observations are between 35 and 90.
To know more about median, refer here:
https://brainly.com/question/3515636
#SPJ4