Darryl has $12 to spend on snacks after he buys his movie ticket.He buys a $6.50 popcorn.if he spends the rest of his money on $2.10 candy bar’s, how many bars can he buy ?
Answers
-6.50 on both sides
2.10x = 5.5
/2.10 on both sides
x = 2.6
Answer:
Darryl can buy 2 snacks.
Related Questions
Are you smarter than a second-grader? A random sample of 55 second-graders in a certain school district are given a standardized mathematics skills test. The sample mean score is x=49. Assume the standard deviation of test scores is -15. The nationwide average score on this test is 50. The school superintendent wants to know whether the second-graders in her school district have weaker math skills than the nationwide average. Use the a-0.01 level of significance and the P-value method with the TI-84 calculator.
Answers
The test statistic for the sample mean is given byz = (x - μ) / (σ / √n)Where,x = 49, μ = 50, σ = 15, n = 55z = (49 - 50) / (15 / √55)≈ -1.24 From the z-tables, we find that the area to the left of z = -1.24 is 0.1089. This implies that the p-value = 0.1089 > α = 0.01.
Given information Random sample of 55 second-gradersSample mean score is x=49The standard deviation of test scores is σ = 15The nationwide average score on this test is 50.The school superintendent wants to know whether the second-graders in her school district have weaker math skills than the nationwide average.Level of significance (α) = 0.01Null hypothesis (H0):
The average math score of second-graders in the school district is greater than or equal to the nationwide average math score.Alternative hypothesis (Ha): The average math score of second-graders in the school district is less than the nationwide average math score.The test statistic for the sample mean is given byz = (x - μ) / (σ / √n)Where,x = 49, μ = 50, σ = 15, n = 55z = (49 - 50) / (15 / √55)≈ -1.24 From the z-tables, we find that the area to the left of z = -1.24 is 0.1089. This implies that the p-value = 0.1089 > α = 0.01.Since the p-value is greater than the level of significance, we fail to reject the null hypothesis.
To know more about statistic refer to
https://brainly.com/question/31577270
#SPJ11
Jenny and Sharon shared 14 toffees in the ratio of 2:5. How many shares will Sharon have? Show all workings.
Answers
The number of toffees Sharon got is 10.
Ratio expresses the relationship between two or more numbers. It shows the frequency of the number of times that one value is contained within other value(s).
Number of toffees Sharon has = (ratio of toffees Sharon got / sum of ratios) x total toffees shared.
Sum of ratios -= 2 + 5 = 7
(5/7) x 14 = 10
To learn more about ratios, please check: https://brainly.com/question/17995727
Explain your reasoning

Answers
The function g(x) can be derived from f(x) by vertical dilation and vertical translation. f(x) = (13 / 4) · x³ - (1 / 2) · x² + (7 / 4) · x + 3 / 2 and g(x) = (125 / 7306) · x³ - (125 / 47789) · x² + (875 / 94978) · x + 375 / 47489 + 2.502.
What kind of rigid translations should we use to modify a function and generate another one?
In this question we must infer what kinds of rigid transformations were used to obtain g(x) in terms of f(x). Points A and B belong to the function f(x) and points A' and B' lie on the curve of function g(x). Rigid transformations are transformations applied on functions such that Euclidean distance is conserved.
We noticed the use of rigid transformations on f(x) such that g(x) is found:
Vertical dilation
f'(x) = k · f(x), where k > 0
Vertical translation
g(x) = k · f(x) + c, where c is the translation factor.
We notice that both f(x) and g(x) are both cubic functions. The former has a vertex at (x, y) = (0, 1.5). First, we determine the coefficients of f(x) by solving the following system of linear equations:
(x₁, y₁) = (1, 6), (x₂, y₂) = (- 2, - 30), (x₃, y₃) = (0, 1.5), (x₄, y₄) = (- 1, - 4)
a + b + c + d = 6
- 8 · a + 4 · b - 2 · c + d = - 30
d = 1.5
- a + b - c + d = - 4
The solution of the system is (a, b, c, d) = (13 / 4, - 1 / 2, 7 / 4, 3 / 2). Then, the expression for the function f(x) is f(x) = (13 / 4) · x³ - (1 / 2) · x² + (7 / 4) · x + 3 / 2.
Now we evaluate the function f(x) at x = 7 and x = - 8:
f(7) = (13 / 4) · 7³ - (1 / 2) · 7² + (7 / 4) · 7 + 3 / 2
f(7) = 1104
f(- 8) = (13 / 4) · (- 8)³ - (1 / 2) · (- 8)² + (7 / 4) · (- 8) + 3 / 2
f(- 8) = - 3417 / 2
Now we determine the coefficient of dilation and the translation factor:
f(7) = 1104, f(- 8) = - 3417 / 2, g(7) = 2.5, g(- 8) = - 6.5
2.5 = 1104 · k + c
- 6.5 = - 3417 · k / 2 + c
The solution of the system of linear equations is (k, c) = (250 / 47489, 2.494). Then, we find that the expression for g(x) is g(x) = (250 / 47489) · [(13 / 4) · x³ - (1 / 2) · x² + (7 / 4) · x + 3 / 2] + 2.494, whose simplest form is:
g(x) = (125 / 7306) · x³ - (125 / 47789) · x² + (875 / 94978) · x + 375 / 47489 + 2.494
g(x) = (125 / 7306) · x³ - (125 / 47789) · x² + (875 / 94978) · x + 375 / 47489 + 2.502
The function g(x) can be derived from f(x) by vertical dilation and vertical translation. f(x) = (13 / 4) · x³ - (1 / 2) · x² + (7 / 4) · x + 3 / 2 and g(x) = (125 / 7306) · x³ - (125 / 47789) · x² + (875 / 94978) · x + 375 / 47489 + 2.502.
To learn more on rigid transformations: https://brainly.com/question/1761538
#SPJ1
[Prompt]If Sam has three-fourths (3/4) of a yard of pipe, how many pieces can he cut the pipe into if each piece is one-eighth (1/8) yard?
Answers
If Sam has three-fourths (3/4) of a yard of pipe, then 6 pieces can he cut the pipe into if each piece is one-eighth (1/8) yard.
In the given question,
Sam has three-fourths (3/4) of a yard of pipe.
We have to find how many pieces can he cut the pipe into if each piece is one-eighth (1/8) yard.
Total length of a yard of pipe is 3/4.
We have to cut the a yard of pipe in the size of 1/8.
Since we have to distribute the 3/4 in 1/8 so we divide 3/4 by 1/8 to find the answer.
Now the expression should be
\(=\frac{3/4}{1/8}\)
To solve this expression multiply 8 on numerator and denominator.
We multiply 8 on both numerator and denominator because when we include any number by our self then we have to perform the same on both side.
\(=\frac{3/4\times8}{1/8\times8}\)
Simplifying
\(=\frac{3\times2}{1}\)
\(={3\times2}\)
\(=6\)
Hence, if Sam has three-fourths (3/4) of a yard of pipe, then 6 pieces can he cut the pipe into if each piece is one-eighth (1/8) yard.
To learn more about the distribution link is here
https://brainly.com/question/14310262
#SPJ1
Sharon filled the bathtub with 33 gallons of water. How many quarts of water did she put in the bathtub?
A.132
B.198
C.66
D.264
Answers
1 gallon = 4 quarts
10 gallons = 40 quarts
30 gallons = 120 quarts
3 gallons = 12 quarts
33 gallons = 132 quarts
Answer: A. 132 quarts
Hope this helps!
The following multiple regression output was generated from a study in which two independent variables are included. The first independent variable (X1) is a quantitative variable measured on a continuous scale. The second variable (X2) is qualitative coded 0 if Yes, 1 if No.Based on this information, which of the following statements is true?If tested at the 0.05 significance level, the overall model would be considered statistically significant.The variable X1 has a slope coefficient that is significantly different from zero if tested at the 0.05 level of significance.The model explains nearly 63 percent of the variation in the dependent variableAll of the above are true.
Answers
All of the claims about the multiple regression output are correct. The first independent variable (X1) was a continuous-scale quantitative variable, whereas the second variable (X2) was coded 0 if Yes and 1 if No.
Multiple regression is an effective statistical approach for analyzing the associations between multiple independent variables and a single dependent variable. Multiple regression has numerous uses in the social sciences, and recent research used it to analyze the connection between two independent factors and a single dependent variable.
Finally, the total model is statistically significant, the slope coefficient for variable X1 is considerably different from zero, and the model explains almost 63% of the variance in the dependent variable.
Learn more about multiple regression here:
https://brainly.com/question/29657622
#SPJ4
A pancake requires 4 cups of flour for every 16 pancakes. How much flour is used per pancake?
Answers
Answer:
The correct answer is 0.25 cups of flour also written as 1/4 cups of flour
Step-by-step explanation:
HAVE A GOOD DAY!
Answer:
1/4 cup of flour for every pancake
Step-by-step explanation:
Divide 16 by 4 to get 4
Divide 4 by 4 to get 1
Divide 1 by 4 to get 1/4.
So a pancake requires 1/4 cup of flour for every pancake.
Miguel made 6 identical necklaces each, having beads and a pendant. The total cost of the beads and the pendant for all 6 necklaces was $29.40. If the beads cost a total of $19.80, how much did each pendant cost?
Answers
Answer:
29.40-19.80=9.6
9.6/6=1.6
So the answer is $1.60
Step-by-step explanation:
work out the total area of the shape 6cm 4cm 3 cm
Answers
Answer:
72
Step-by-step explanation:
multiply all the sides
24
3
72
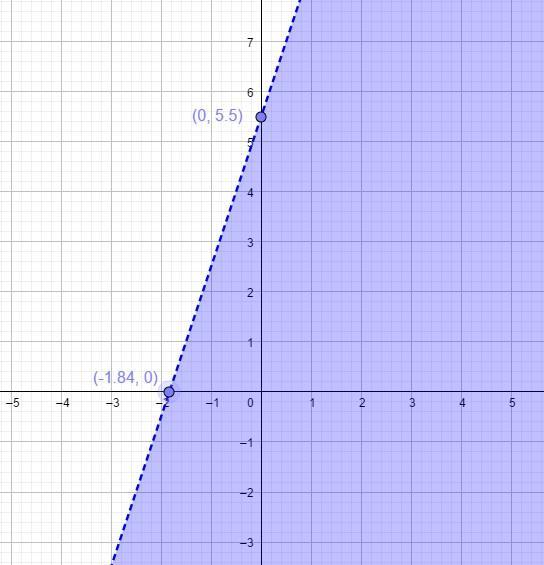
Graph for 6x - 2y > -11
Answers
To graph the inequality:
\(6x-2y>-11\)We use the x and y-intercepts.
When x=0
\(\begin{gathered} 6x-2y>-11 \\ 6(0)-2y>-11 \\ -2y>-11 \\ \frac{-2y}{-2}<\frac{-11}{-2} \\ y<5.5 \end{gathered}\)We have the point: (0, 5.5)
When y=0
\(\begin{gathered} 6x-2y>-11 \\ 6x>-11 \\ x>\frac{-11}{6} \\ x>-1.83 \end{gathered}\)We have the point: (-1.83, 0)
We plot the points (0, 5.5) and (-1.83,0).
The points are joined using a broken line because of the inequality sign: >
The graph is shown below:
To determine which side is required, we use the origin test.
When x=0 and y=0
\(\begin{gathered} 6x-2y>-11 \\ 0>-11\text{ (TRUE)} \end{gathered}\)This means the side of the line containing (0,0) is where we need. (Shaded above)
please help me!
NO BOTS

Answers
Answer:
16 < 24 < 25
Step-by-step explanation:
√16 = 4
√25 = 5
If a candy machine contains 76 green candies, 42 orange candies, 58 red
candies, and 24 yellow candies, what is the probability that a candy chosen at
random will be red?
Answers
Answer:
P(candy chosen is red) = 58/200
Step-by-step explanation:
0.29 is the probability that a candy chosen at random will be red.
What is probability?The probability exists the branch of mathematics involving numerical descriptions of how likely an event exists to happen, or how likely it exists that a proposition stands true. The probability of an event exists in a number between 0 and 1, where, roughly speaking, 0 reveals the impossibility of the event, and 1 demonstrates certainty.
A machine contains = 76 green candies
B machine contains = 42 orange candies
C machine contains = 58 red candies
D machine contains = 24 yellow candies
Probability = 58 / 76 + 42+ 58+ 24
= 58 / 200
= 0.29
0.29 is the probability that a candy chosen at random will be red.
To learn more about probability refer to:
https://brainly.com/question/13604758
#SPJ2
pleaseeeeee help!!!!!!!!!!

Answers
Answer:
The conditions for calculating a confident surgery were clearly not past.
Step-by-step explanation:
When you are testing a vaccine of a surgery, there needs to be a over 60% success rate at which the vaccine of the surgery is affective, otherwise, it is decided that that medical procedure of medicine isn't safe. There have been some exceptions in the past when a vaccine for example was used with a 40% success rate, only because the public required this vaccine in there time.
Only 1/9 enrolled students in a school were absent. There were 4512 students present. How many students are enrolled in the school?
Answers
Answer:
5076.
Step-by-step explanation:
Let x be the number enrolled, then:
x - 1/9 x = 4512
8/9x = 4512
x = 4512 * 9/8
x = 5076.
Which of the following could be a real-world description of 5x − 18?
$18 in addition to the cost of 5 hot dog combos
The cost of 18 people splitting 5 hot dog combos
The cost of hot dog combos less an $18 coupon split by 5 people
$18 less than the cost of 5 hot dog combos
Answers
Answer:
$18 less than the cost of 5 hot dog combos
Step-by-step explanation:
First, we see from the minus sign that this will be subtraction. PEMDAS (order of operations) says we do the multiplication first, then the subtraction.
A sales position needs to be filled. There are two candidates available. The first candidate has 10 years of experience and can sell 10 units a week making a $3,000 profit per week for the company. He is asking for $80,000 salary. The second candidate has one year of experience and can sell eight units a week making a $2,400 profit for the company. He is asking for $45,000 salary. What candidate would make the company the most money their first year of employment?.
Answers
The candidate that would make the company the most money in their first year of employment is Candidate B
Which candidate would make more money?The amount of profit that a candidate can make for the company is:
= ( Number of weeks in year x Profit per week ) - Salary for the year
We shall assume 48 working weeks in a year.
The amount of money made by Candidate A would be:
= ( 48 x 3, 000 ) - 80, 000
= $64, 000
The amount of money made by Candidate B is:
= ( 48 x 2, 400 ) - 45, 000
= $70, 200
Find out more on salesperson at https://brainly.com/question/24951536
#SPJ1
consider the following initial value problem, in which an input of large amplitude and short duration has been idealized as a delta function. find the laplace transform of the solution. 9/s-9/(s 1) e^(-2s)/(s 1) obtain the solution . 9-9e^-t e^(-t 2)theta(t-2)
Answers
For an initial value problem with condition, y′ + y = 4 + δ(t - 3), y(0)=0,
a) The Laplace transform of the solution is equals to the \(Y(s) = \frac{1}{s + 1}( \frac{4}{s} + \frac{e^{ - 3s}}{s})\).
b) The solution is \(y(t) = 4 - 4e^{-t} ( 1 - e^{ 2 - t}) δ(t−3) \).
Using Laplace transformation, we can easily solve the initial value differential problems. To solve these differential equation using Laplace, we first calculate the Laplace transform of the equation then we take inverse Laplace transformation. We have an initial value problem and condition, y′ + y = 4 + δ(t - 3), --(1) y(0)= 0, where an input of large amplitude and short duration has been idealized as a delta function. We have to solve it using Laplace transform.
a) The objective is to determine the Laplace transform Y(s). Taking Laplace transformation on both sides of equation(1), L(y′ + y) = L(4 + δ(t−3))
=> L(y′) + L(y) = L(4) + L(δ(t−3))
\((sY(s) - y(0))+ Y(s) = \frac{4}{s} + \frac{e^{−3s}}{s} \\ \)
Substitute the initial values in equation,
\(( 1 + s) Y(s) - 0 = \frac{4}{s} + \frac{e^{ −3s}}{s}\)
\(Y(s) = \frac{1}{s + 1}( \frac{4}{s} + \frac{e^{ - 3s}}{s})\)
so, the Laplace transform is
\(Y(s) = \frac{1}{s + 1}( \frac{4}{s} + \frac{e^{ - 3s}}{s})\).
b) The solution of y(t), that is objective is to determine function y(t). For this, taking inverse Laplace on both sides to determine the function \(y(t) = L^{−1}(\frac{1}{s+1}(\frac{4}{s} + \frac{ e^{-3s}}{s}))\)
\(= L^{−1}(\frac{4}{s( s+1)} + \frac{ e^{-3s}}{s(s+1)})\)
\(= L^{−1}(\frac{4}{s( s+1)} )+ L^{-1}( \frac{ e^{-3s}}{s(s+1)})\).
\(= L^{−1}(\frac{4}{s}) L^{-1}(\frac{4}{s+1} )+ L^{-1}( \frac{ e^{-3s}}{s}) L^{-1}( \frac{e^{-3s}}{s+1}) \\ \).
Evaluate Laplace inverse as, \(y(t) = 4 - 4e^{-t} ( 1 - e^{ 2 - t}) δ(t−3) \). Hence, required value is \(y(t) = 4 - 4e^{-t} ( 1 - e^{ 2 - t}) δ(t−3) \).
For more information about Laplace transformation visit:
https://brainly.com/question/28167584
#SPJ4
Complete question:
Consider the following initial value problem, in which an input of large amplitude and short duration has been idealized as a delta function,
y′ + y = 4 + δ(t−3), y(0)=0.
a) Find the Laplace transform of the solution.
Y(s)=L{y(t)} =
b) Obtain the solution y(t).
y(t)= ?
Find the side length if a square given the are of the square.

Answers
18 inches
Explanation
the area of a square is given by:
\(\begin{gathered} \text{Area}_{square}=side\cdot side \\ \text{Area}_{square}=side^2 \end{gathered}\)then ,let
\(\text{Area}=A=324in^2\)replace
\(\begin{gathered} 324in^2=side^2 \\ \text{square root in both sides} \\ \sqrt[]{324in^2}\text{ = }\sqrt[]{side^2} \\ 18\text{ in=side} \end{gathered}\)therefor, the length of the side is 18 inches.
i hope this helps you

What is the difference?
7-3=
A. 3
B. 4.
O c. 5
OD. 10
O E. 11
Answers
hope this helped
the grade a student received on an examination was transformed to a z value, which was negative. therefore, we know that he scored a) higher than 16 percent of the class.b) higher than 45 percent of the class.c) above the first quartile.d) below the mean.e) lower than 16 percent of the class.
Answers
The student's exam grade was converted to a negative z-score, indicating that they scored below the mean
Therefore, option d is correct.
When a grade is transformed into a z-score, it represents how many standard deviations the grade is away from the mean. The mean is always set at a z-score of 0, and positive z-scores indicate that a grade is above the mean, while negative z-scores indicate that a grade is below the mean.
In this question, the student's exam grade was transformed into a negative z-score, which means that the grade is below the mean. This is because the negative sign in the z-score indicates that the grade is a certain number of standard deviations below the mean. The further the z-score is below 0, the further the grade is below the mean.
Learn more about mean:
brainly.com/question/30112112
#SPJ4
Explain why the square root of a number or variable can be either positive or negative.
Answers
Answer:
Well, the answer is: it depends on what was printed in the problem. The principal square root symbol never has a negative output, so if the test maker printed that symbol, it’s restrictions have to be respected: all square roots then are positive.
Step-by-step explanation:
a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. For example, 4 and −4 are square roots of 16, because 4² = (−4)² = 16. Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by √(x), where the symbol √( ) is called the radical sign or radix.
Answer/Step-by-step explanation:
The square root could be positive or negative because multiplying two negative numbers gives a positive number. The principal square root is the nonnegative number that when multiplied by itself equals a. The square root obtained using a calculator is the principal square root.
Answer all or none! Ty!

Answers
2) The answer is 14.4 miles because that’s what 3.6x4 equals.
3) The answer would be $63.09 because 7.01x9=63.09
4) The answer is 1.35 , you just have to multiply 0.5 and 2.7
5) The answer is 9.432 seconds
6) For aluminum it would be $1.15 and for copper it would be $3.24
7) 0.21 x 10 = 2.1
8) 45.35 divided by 10,000 = 0.004535
9) 6.02 x 0.1 = 0.602
10) 9.4 divided by 0.01 = 940
11) 15.5
12) $695
Please help me!!! I would very much appreciate it
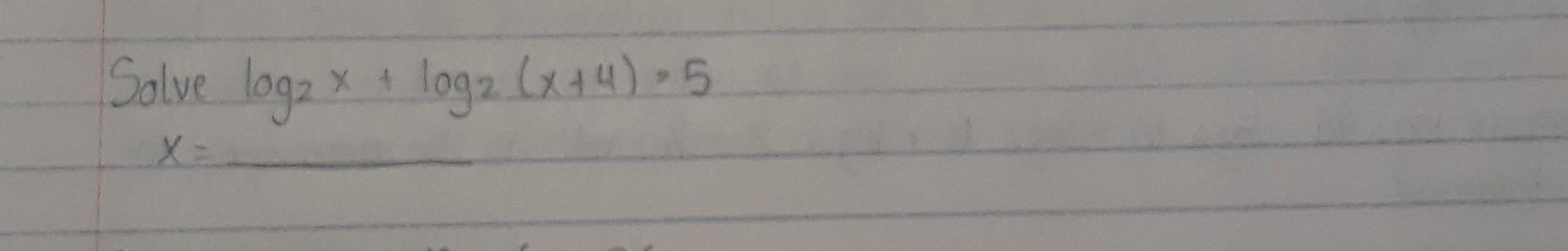
Answers
Answer:
x=4
Step-by-step explanation:
hope it helps thanks



Find the value of m if polynomial p(x) = 4x2 – 6x – m is exactly divisible by x – 3.
Answers
Answer:
Since p(x) is exactly divisible by x – 3, then p(3) = 0.
Plugging in x = 3 into p(x), we get
4(3)2 – 6(3) – m = 0
36 – 18 – m = 0
m = 18
Therefore, the value of m is 18.
Step-by-step explanation:
11x + 15y = 3 y intercept
Answers
Answer:
y-int = 0.2
Step-by-step explanation:
hope this helps ? :)
Solve the system of equations by Substitution. Show ALL your work.
4x2 + y2 = 4
y = x + 2
Answers
The system of equations has two solutions: (0,2) and (-4/5, -6/5).
Define Substitution methodThe substitution method is a way to solve a system of two linear equations with two variables. The method involves solving one of the equations for one of the variables, and then substituting that expression into the other equation in place of the same variable. This process reduces the system of two equations and two variables to a single equation and a single variable, which can then be solved.
We have the system of equations:
4x² + y² = 4 ........(1)
y = x + 2 ........(2)
We can solve this system of equations by substitution.
Substitute (2) into (1) to eliminate y:
4x² + (x + 2)² = 4
Simplify and solve for x:
4x² + x² + 4x + 4 = 4
5x²+ 4x = 0
x(5x + 4) = 0
x = 0 or x = -4/5
If x = 0, then from equation (2), y = 2. So one solution is (x,y) = (0,2).
If x = -4/5, then from equation (2), y = -6/5. So the other solution is (x,y) = (-4/5, -6/5).
Therefore, the system of equations has two solutions: (0,2) and (-4/5, -6/5).
To know more about eliminate, visit:
https://brainly.com/question/20523886
#SPJ1
Calculate Unit Rates
please help
Find the unit rate for each problem.

Answers
Answer:
1. 3 tacos per person
2. 8 chairs per table
3. 6 avocados per bag
Step-by-step explanation:
1) Divide 45 by 15 to get the unit rate: # of taco per person.
45 = 15x
45/15 = 15x/15
3 = x
3 tacos per person
2) Divide 72 by 9 to get the unit rate: # of chairs per table.
72 = 9x
72/9 = 9x/9
8 = x
8 chairs per table
3) Divide 42 by 7 to get the unit rate: # of avocados per bag.
42 = 7x
42/7 = 7x/7
6 = x
6 avocados per bag
If the slope is -1/4 and the point (-2,7) is on the line,
what is the equation of the line in point slope form?

Answers
y = mx + b
y = -1/4x + b
7 = -1/4(-2) + b
7 = 1/2 + b
2(7 = 1/2 + b)
14 = 1 + 2b
-1 -1
13 = 2b
/2 /2
13/2 or 6.5 = b
y = -1/4x + 13/2 or 6.5
Point Slope Form:
y - y1 = m (x - x1)
y - 7 = -1/4 (x - -2)
y - 7 = -1/4 (x + 2)
y - 7 = -1/4x - 1/2
+ 7 + 7
y = -1/4x + 13/2
Hope that helps!
Quiz Active
1
2
B
8
The figure shows five points. A point has been translated right and up.
D
9 10
Based on the graph, which statements about the points could be true? Check all that apply.
Answers
The point (5, 10) has not been translated in the given figure.Hence this statement is false.
The graph shows five points.
A point has been translated right and up.
Now, the statements that are true based on the graph are as follows:
The point (9, D) has been translated right and up.Answer: False
There is no information given about point (9, D).
So, we cannot say anything about the translation of point (9, D).
The point (1, 8) has been translated right and up.Answer: True
As explained above, the point (1, 8) has been translated 7 units to the right and 2 units up to get the new point (8, 10). So, this statement is true.
The point (2, 9) has been translated right and up.Answer: False
The point (2, 9) has not been translated in the given figure.
So, this statement is false.
Statement 4: The point (8, B) has been translated right and up.Answer: True
The point (8, B) has been translated 1 unit up in the given figure. So, this statement is true.
The point (5, 10) has been translated right and up.Answer: False
The point (5, 10) has not been translated in the given figure.
So, this statement is false.
For more questions on translated:
https://brainly.in/question/33380281
#SPJ8
Solve the equation for x

Answers
Answer:
the answer is 5
Step-by-step explanation:
2x/5 - 9 = -7
2x/5 = -7 + 9
2x/5 = 2
2x = 2 * 5
2x = 10
x = 10/2
x = 5
Answer:
x = 5
Step-by-step explanation:
2
--- x - 9 = -7 add 9 both sides
5
2
--- x - 9 + 9 = -7 + 9
5
2
--- x = 2 multiply both sides by 5
5
2
5 * --- x = 2 * 5
5
2x = 10
x = 10 / 2
x = 5